10.2: The Fundamental Theorem of Algebra

We have seen in Observation(Remainder) that every root \(c\) of a polynomial \(f(x)\) gives a factor \((x-c)\) of \(f(x)\). There is a theorem which says something about the existence of roots and factors but we will need to discuss complex numbers briefly before stating that theorem.

As stated above, we know that there is no real number that satisfies \(x^2=-1\). So we define \(i\) to be a solution to this equation. This \(i\) is not a real number but a new kind of number called a complex number. We can think of \(i\) as \(\sqrt{-1}\). We can now consider numbers of the form \(a+ib\) where \(a\) and \(b\) are real numbers. Numbers of this form constitutes the set of complex numbers, denoted by \(\mathbb{C}\). \(a\) is called the real part and \(b\) is called the imaginary part of the complex number \(a+i b\). We can add two complex numbers by adding their real and imaginary parts to form the real and imaginary parts of the sum. We can multiply two complex numbers by ordinary distribution (FOIL) then use the property that \(i^2=-1\).

Example \(\PageIndex{1}\)

We have

\[(2-3i)-(4+3i)=(2-4)+(-3-3)i=-2-6i \nonumber \]

and

\[(2-3i)(4+3i)=8+6i-12i-9i^2=8-6i-9(-1)=17-6i \nonumber \]

We can see by writing, for example, \(\sqrt{-6}=i\sqrt{6}\), that these numbers arise naturally as roots of quadratic equations. But there is more! The following fundamental theorem of algebra guarantees the existence of roots of any polynomial.

Theorem (Fundamental Theorem of Algebra)

Let \(f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}\), be a non-constant polynomial. Then there exists a complex number \(c\) which is a root of \(f\).

Let us make two remarks about the fundamental theorem of algebra to clarify the statement of the theorem.

Note

• In the above Theorem we did not specify what kind of coefficients \(a_0,\dots a_n\) are allowed for the theorem to hold. In fact, to be precise, the fundamental theorem of algebra states that for any complex numbers \(a_0,\dots a_n\), the polynomial \(f(x)=a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) has a root.
• In general there may not exist a real root \(c\) of a given polynomial, but the root \(c\) may only be a complex number. For example, consider \(f(x)=x^2+1\), and consider the roots \(c\) of \(f\), that is \(c^2+1=0\). Then, for any real number \(c\), we have always \(c^2\geq 0\), so that \(f(c)=c^2+1\geq 1\), so that there cannot be a real root \(c\) of \(f\). However, if we multiply \[(x-i)(x+i)=x^2+xi-xi-i^2=x^2+1 \nonumber \] we see that \(f\) has complex roots \(c=i\) and \(c=-i\).

Now, while the fundamental theorem of algebra guarantees a root \(c\) of a polynomial \(f\), we can use the remainder theorem from Observation(Remainder) to check possible candidates \(c\) for the roots, and the factor theorem to factor \(f(x)=q(x)\cdot (x-c)\).

Example \(\PageIndex{2}\)

Find roots of the given polynomial and use this information to factor the polynomial completely.

1. \(f(x)=2x^3-8x^2-6x+36\)
2. \(f(x)=x^4-3x^3-36x^2+68x+240\)
3. \(f(x)=x^3+1\)
4. \(f(x)=x^4-16\)

Solution

1. In order to find a root, we use the graph to make a guess for one of the roots.

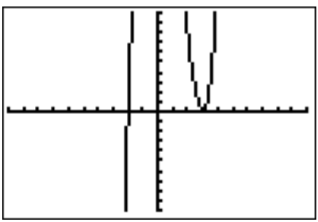
The graph suggests that the roots may be at \(x=-2\) and \(x=3\). This is also supported by looking at the table for the function.

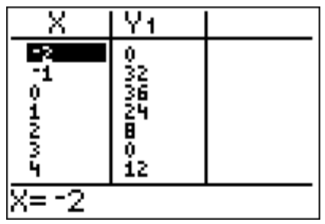
We check that these are roots by plugging the numbers into the function.

\[\begin{aligned} f(-2)&= 2\cdot (-2)^3-8\cdot (-2)^2-6\cdot (-2)+36=-16-32+12+36=0\\ f(3)&= 2\cdot 3^3-8\cdot 3^2-6\cdot 3+36=54-72-18+36=0\end{aligned} \nonumber \]

By the factor theorem we can divide \(f(x)=2x^3-8x^2-6x+36\), for example, by \((x-3)\).

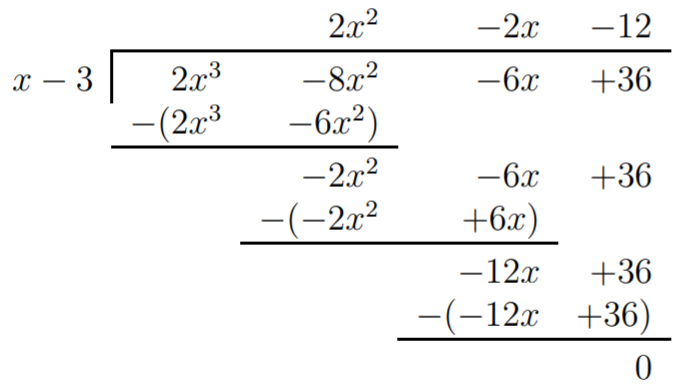
Therefore, \(f(x)=(2x^2-2x-12)(x-3)\). To factor \(f\) completely, we still need to factor the first polynomial \(2x^2-2x-12\):

\[\begin{aligned} f(x)&=(2x^2-2x-12)(x-3)\\ &=2\cdot(x^2-x-6)\cdot (x-3)\\ &= 2\cdot (x-3)\cdot(x+2)\cdot (x-3)\\ &=2\cdot (x+2)\cdot (x-3)^2 \end{aligned} \nonumber \]

2. The graph of \(f(x)=x^4-3x^3-36x^2+68x+240\) in the standard window is the following:

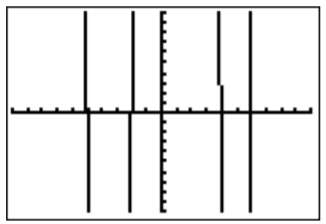
We suspect that \(x=-5\), \(x=-2\), \(x=4\), and \(x=6\) are the roots of the function. This is confirmed by checking the table on the calculator, and also by direct computation.

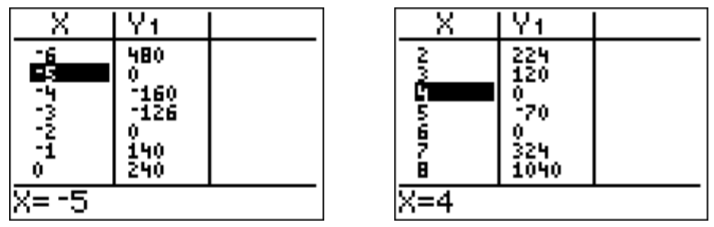
\[\begin{aligned} f(-5)&=(-5)^4-3(-5)^3-36(-5)^2+68(-5)+240 =0\\ f(-2)&=(-2)^4-3(-2)^3-36(-2)^2+68(-2)+240 =0\\ f(4)&=4^4-3\cdot 4^3-36\cdot 4^2+68\cdot 4+240 =0\\ f(6)&=6^4-3\cdot 6^3-36\cdot 6^2+68\cdot 6+240 =0\end{aligned} \nonumber \]

Therefore, each \((x+5)\), \((x+2)\), \((x-4)\), and \((x-6)\) is a factor of \(f(x)\), and then their product is also a factor of \(f(x)\). The product \((x+5)(x+2)(x-4)(x-6)\) is calculated as follows. Since \((x+5)(x+2)=x^2+7x+10\) and \((x-4)(x-6)=x^2-10x+24\), we obtain

\[\begin{aligned} (x+5)(x+2)(x-4)(x-6) &= ({\color{Red} {x^2}}+{\color{Blue} {7x}}+{\color{Green} {10}})(x^2-10x+24) \\ &={\color{Red} {x^4-10x^3+24x^2}}{\color{Blue} {+7x^3-70x^2+168x}}{\color{Green} {+10x^2-100x+240}} \\ &=x^4-3x^3-36x^2+68x+240\\ &=f(x)\end{aligned} \nonumber \]

We see that this is precisely \(f(x)\), so that no more polynomial division is necessary. The answer is \(f(x)=(x+5)(x+2)(x-4)(x-6)\).

3. We can graph the function, or just make a guess for a root of \(f(x)=x^3+1\). An immediate guess would be to try \(x=-1\). This is indeed a root, since \(f(-1)=(-1)^3+1=-1+1=0\), which is also supported by the graph.

Therefore, we can divide \(x^3+1\) by \(x+1\).

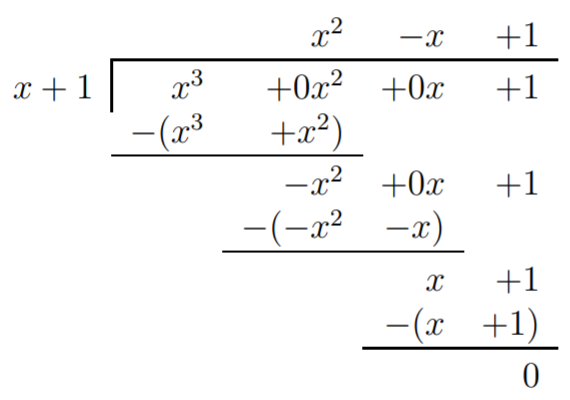
We obtain \(f(x)=x^3+1=(x^2-x+1)(x+1)\). Now \(x+1\) cannot be factored any further, however, we may continue to factor \(x^2-x+1=(x-x_1)(x-x_2)\). Using the quadratic formula, we obtain the solutions of \(x^2-x+1=0\) as

\[x_{1/2}=\dfrac{-(-1)\pm\sqrt{(-1)^2-4\cdot 1\cdot 1}}{2\cdot 1}=\dfrac{1\pm\sqrt{-3}}{2} =\dfrac 1 2 \pm i \dfrac{\sqrt{3}}{2} \nonumber \]

Therefore, \(x^3+1=\left (x-\left (\dfrac 1 2 + i\dfrac{\sqrt{3}}{2} \right ) \right )\cdot \left (x- \left (\dfrac 1 2 - i\dfrac{\sqrt{3}}{2} \right ) \right )\cdot (x+1)\).

4. For \(f(x)=x^4-16\) there are the two obvious candidates \(x=2\) and \(x=-2\) that we can identify as roots, either by guessing (since \(2^4=16\)) or by looking at the graph.

Indeed the algebra confirms these guesses.

\[\begin{aligned} f(2)&= 2^4-16=16-16=0\\ f(-2)&= (-2)^4-16=16-16=0\end{aligned} \nonumber \]

Therefore, \(f(x)=q(x)\cdot (x-2)\cdot (x+2)=q(x)\cdot (x^2-4)\). To find \(q(x)\) we perform the long division \((x^4-16)/(x^2-4)\).

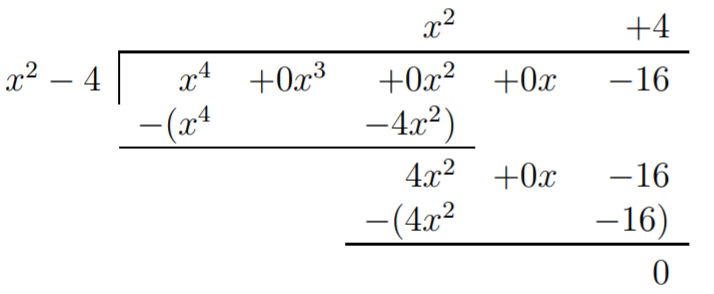
We obtain \(f(x)=(x^2+4)(x+2)(x-2)\). The roots of \(x^2+4\) are given by the quadratic formula as

\[x_{1/2}=\dfrac{-0\pm\sqrt{0^2-4\cdot 1\cdot 4}}{2\cdot 1}=\pm\dfrac{\sqrt{-16}}{2}=\pm\dfrac{4i}{2}=\pm 2i \nonumber \]

or alternatively, \(x^2+4=0\implies x^2=-4\implies x=\pm 2i\). We obtain the factored polynomial \(f(x)=(x+2i)(x-2i)(x+2)(x-2)\).

As we have seen in the last example, we can use the roots to factor a polynomial completely so that all factors are polynomials of degree \(1\) only. Furthermore, whenever a complex root, \(a+ib\), appeared, its conjugate, \(a-ib\), was also a root. These remarks hold more generally, as we state now.

Observation: General Polynomial

1. Every polynomial \(f(x)=a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) of degree \(n\) can be factored as \[f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot \dots \cdot (x-c_n) \nonumber \]
2. In particular, every polynomial of degree \(n\) has at most \(n\) roots. (However, these roots may be real or complex.)
3. The factor \((x-c)\) for a root \(c\) could appear multiple times in the above product, that is, we may have \((x-c)^k\) as a factor of \(f\). The multiplicity of a root \(c\) is the number of times \(k\) that a root appears in the factored expression for \(f\) as in (1).
4. If \(f(x)=a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) has only real coefficients \(a_0,\dots, a_n\), and \(c=a+bi\) is a complex root of \(f\), then the complex conjugate \(\bar c=a-bi\) is also a root of \(f\).
   • Proof: If \(x\) is any root, then \(a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0=0\). Applying the complex conjugate to this and using that \(\overline{u\cdot v}=\bar u \cdot \bar v\) gives \(\overline{a_n} \bar{x}^n+\overline{a_{n-1}}\bar{x}^{n-1}+\dots+\overline{a_1} \bar x+\overline{a_0}=0\). Since the coefficients \(a_j\) are real, we have that \(\overline{a_j}=a_j\), so that \(a_n \bar x^n+a_{n-1}\bar x^{n-1}+\dots+a_1 \bar x+a_0=0\). This shows that the complex conjugate \(\bar x\) is a root of \(f\) as well.

Example \(\PageIndex{3}\)

Find the roots of the polynomial and sketch its graph including all roots.

1. \(f(x)=x^3+2x^2-14x-3\)
2. \(f(x)=x^4-7x^3+11x^2-7x+10\)

Solution

1. To find a root, we first graph the function \(f(x)=x^3+2x^2-14x-3\) with the calculator. The graph and the table suggest that we have a root at \(x=3\).

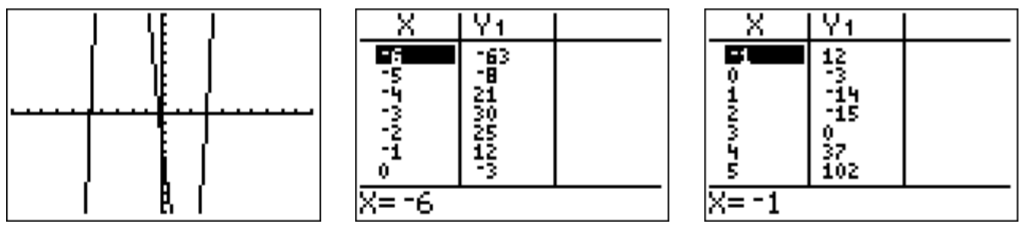
Therefore we divide \(f(x)\) by \((x-3)\). We obtain:

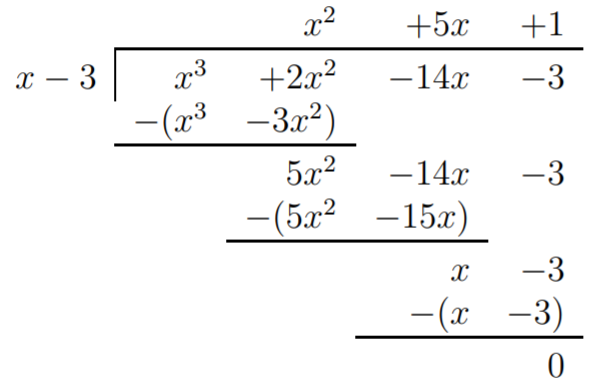
This shows that \(f(x)=(x-3)(x^2+5x+1)\). To find the roots of \(f\), we also have to find the roots of the second factor \(x^2+5x+1\), i.e., the solutions to \(x^2+5x+1=0\). The quadratic formula gives:

\[x=\dfrac{-5\pm\sqrt{5^2-4\cdot 1 \cdot 1}}{2\cdot 1}=\cfrac{-5\pm\sqrt{21}}{2} \nonumber \]

The roots are therefore:

\[x=3, \quad\quad x=\dfrac{-5+\sqrt{21}}{2}\approx -0.2, \quad\quad x=\dfrac{-5-\sqrt{21}}{2}\approx -4.8 \nonumber \]

We put these roots together with the graph in an appropriate window.

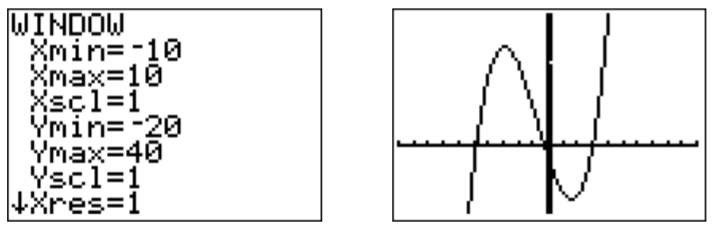
The graph including the roots is displayed below.

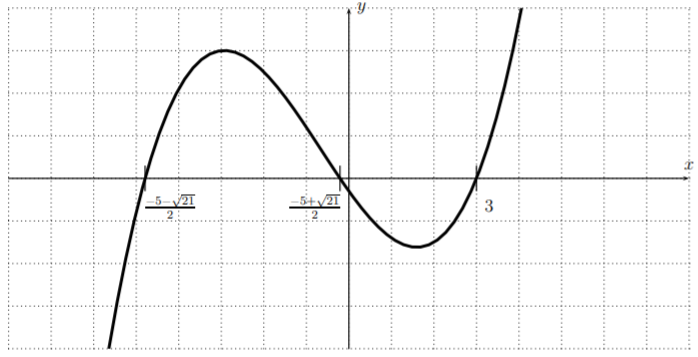
2. The graph of \(f(x)=x^4-7x^3+11x^2-7x+10\) in an appropriate window suggests the roots \(x=2\) and \(x=5\).

Dividing \(f(x)\) by \((x-2)(x-5)=x^2-7x+10\) gives:

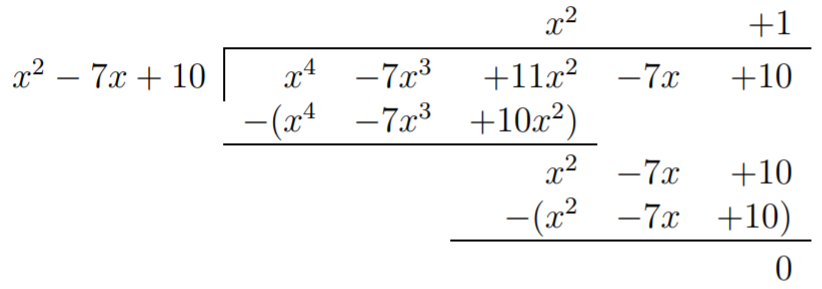
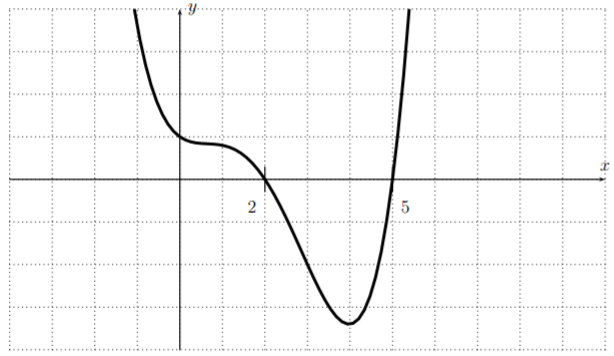
Since the roots of \(x^2+1\) are all complex, we see that the only roots of \(f\) are \(x=2\) and \(x=5\). The graph including its roots is displayed below.

Example \(\PageIndex{4}\)

Find a polynomial \(f\) with the following properties.

1. \(f\) has degree \(3\), the roots of \(f\) are precisely \(4\), \(5\), \(6\), and the leading coefficient of \(f\) is \(7\)
2. \(f\) has degree \(3\) with real coefficients, \(f\) has roots \(3i\), \(-5\) (and possibly other roots as well), and \(f(0)=90\)
3. \(f\) has degree \(4\) with complex coefficients, \(f\) has roots \(i+1\), \(2i\), \(3\)
4. \(f\) has degree \(5\) with real coefficients, the leading coefficient is 1, and the roots are determined by its graph:

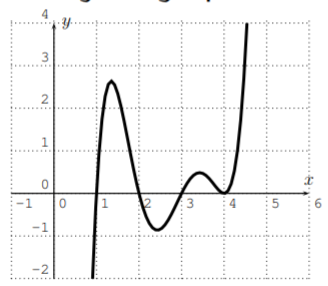
Solution

1. In general a polynomial \(f\) of degree \(3\) is of the form \(f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot (x-c_3)\). Identifying the roots and the leading coefficient, we obtain the polynomial \[f(x)=7 \cdot (x-4)\cdot (x-5)\cdot (x-6) \nonumber \]
2. A polynomial \(f\) of degree \(3\) is of the form \(f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot (x-c_3)\). Roots of \(f\) are \(3i\) and \(-5\), and since the coefficients of \(f\) are real it follows from General Polynomial Observation(4), that the complex conjugate \(-3i\) is also a root of \(f\). Therefore, \(f(x)=m\cdot (x+5)\cdot (x-3i)\cdot (x+3i)\). To identify \(m\), we use the last condition \(f(0)=90\). \[90 = m\cdot (0+5)\cdot (0-3i)\cdot (0+3i)=m\cdot 5\cdot (-9)i^2=m\cdot 5\cdot 9=45 m \nonumber \] Dividing by \(45\), we obtain \(m=2\), so that \[f(x)=2\cdot (x+5)\cdot (x-3i)\cdot (x+3i)=2\cdot (x+5)\cdot (x^2+9) \nonumber \] which clearly has real coefficients.
3. Since \(f\) is of degree \(4\) it can be written as \(f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot (x-c_3)\cdot (x-c_4)\). Three of the roots are identified as \(i+1\), \(2i\), and \(3\): \[f(x)=m\cdot (x-(1+i))\cdot (x-2i)\cdot (x-3)\cdot (x-c_4) \nonumber \] However, we have no further information on the fourth root \(c_4\) or the leading coefficient \(m\). (Note that General Polynomial Observation(4) cannot be used here, since we are not assuming that the polynomial has real coefficients. Indeed it cannot have real coefficients since that would mean we would have also the complex conjugates of \(1+i\) and \(2i\) in addition to the three that we are given, giving us a total of 5 roots which cannot be accommodated by a polynomial of degree 4.) We can therefore choose any number for these remaining variables. For example, a possible solution of the problem is given by choosing \(m=3\) and \(c_4=2\), for which we obtain: \[f(x)=3\cdot (x-(1+i))\cdot (x-2i)\cdot (x-3)\cdot (x-2) \nonumber \]
4. \(f\) is of degree \(5\), and we know that the leading coefficient is \(1\). The graph is zero at \(x=1, 2, 3\), and \(4\), so that the roots are \(1\), \(2\), \(3\), and \(4\). Moreover, since the graph just touches the root \(x=4\), this must be a multiple root, that is, it must occur more than once (see Section 9.3 for a discussion of multiple roots and their graphical consequences). We obtain the following solution: \[f(x)=(x-1)(x-2)(x-3)(x-4)^2 \nonumber \] Note that the root \(x=4\) is a root of multiplicity \(2\).

Note that to see that a polynomial has real coefficients, it may be necessary to multiply factors like \((x-(2+3i))(x-(2-3i))\). We suggest a way of doing this for which we use the fact that \(a^2-b^2=(a+b)(a-b)\). We have \[(x-(2+3i))(x-(2-3i))=((x-2)-3i)((x-2)+3i)=(x-2)^2+9 \nonumber \] which clearly has real coefficients.