12.2: Rational inequalities and absolute value inequalities

Last updated
Save as PDF

Page ID: 49025

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Rational inequalities are solved with the same three-step process that was used to solve the polynomial and absolute value inequalities before (see page ). That is, in step 1, we find the solution of the corresponding equality, and then, in step 2, we use sample points of the graph to determine the intervals of the solution. Finally, in step 3, we check the endpoints of each interval.

Example $\PageIndex{1}$

Solve for $x$.

$\dfrac{x^2-5x+6}{x^2-5x}\geq 0$
$\dfrac{5}{x-2}\leq 3$
$\dfrac{4}{x+5}<\dfrac{3}{x-3}$
$|2x-3|>7$

Solution

Here is the graph of $\dfrac{x^2-5x+6}{x^2-5x}$ in the standard window.

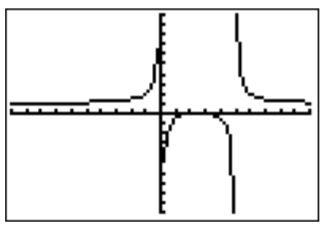
$clipboard_ebd87149b27b30be501fe8bec32454d45.png$

Factoring numerator and denominator, we can determine vertical asymptotes, holes, and $x$-intercepts.

\[\dfrac{x^2-5x+6}{x^2-5x}=\dfrac{(x-2)(x-3)}{x(x-5)} \nonumber \]

The vertical asymptotes are at $x=0$ and $x=5$, the $x$-intercepts are at $x=2$ and $x=3$. Since for large $x$, the fraction reduces to $\dfrac{x^2}{x^2}=1$, we see that the horizontal asymptote is at $y=1$. Thus, $\dfrac{x^2-5x+6}{x^2-5x}\geq 0$ for $x< 0$ and $x>5$. To see where the graph is $\geq 0$ between $0$ and $5$, we zoom into the graph:

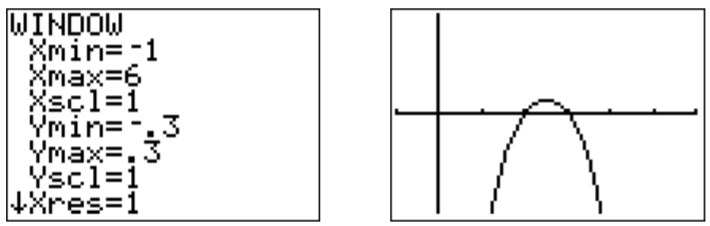
$clipboard_ef3c93b76af25649a789bcf3ecc2db5c3.png$

Combining all of the above information, we obtain the solution set:

\[\text{solution set}=(-\infty,0)\cup[2,3]\cup(5,\infty) \nonumber \]

Notice that the $x-$coordinate of the $x-$intercepts are $x=2$ and $x=3$ are included in the solution set, whereas the values $x=0$ and $x=5$ associated with the vertical asymptotes are not included since the fraction is not defined for $x=0$ and $x=5$.

To find the numbers $x$ where $\dfrac{5}{x-2}\leq 3$, we can graph the two functions on the right and left of the inequality.

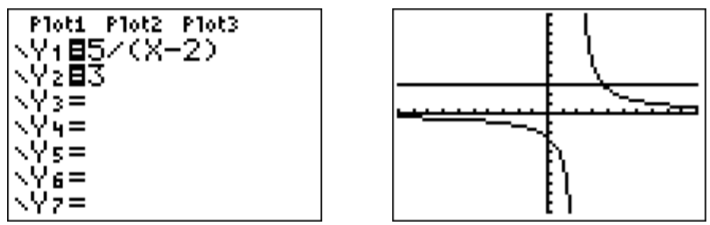
$clipboard_ee97d1a806312249ad4747db4cb49e7dc.png$

However, this can sometimes be confusing, and we recommend rewriting the inequality so that one side becomes zero. Then, we graph the function on the other side of the new inequality.

\[\begin{aligned} \dfrac{5}{x-2}\leq 3 &\implies \quad \dfrac{5}{x-2}-3\leq 0 \implies \quad \dfrac{5-3(x-2)}{x-2}\leq 0\\ & \implies \quad \dfrac{5-3x+6}{x-2}\leq 0 \implies \quad \dfrac{11-3x}{x-2}\leq 0\end{aligned} \nonumber \]

Therefore, we graph the function $f(x)=\dfrac{11-3x}{x-2}$.

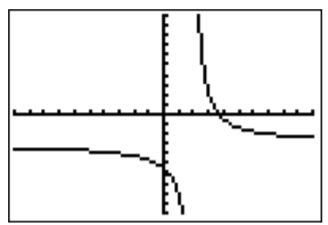
$clipboard_e40ddd7ed22046aa88a318b3cbd3ba9d1.png$

The vertical asymptote is $x=2$, and the $x$-intercept found thus

\[11-3x=0\implies \quad 11=3x \implies \quad x=\dfrac {11}{3} \nonumber \]

This together with the graph and the fact that $f$ is undefined at $2$ and $f(\dfrac{11}{2})=0$ gives the following solution set:

\[\text{solution set}=\Big(-\infty,2\Big)\cup \Big[\dfrac{11}{3},\infty\Big) \nonumber \]

We want to find those numbers $x$ for which $\dfrac{4}{x+5}<\frac{3}{x-3}$. One way to do this is given by graphing both functions $f_1(x)=\dfrac{4}{x+5}$ and $f_2(x)=\dfrac{3}{x-3}$, and by trying to determine where $f_1(x)<f_2(x)$. However this can sometimes be quite confusing, as the two graphs for $f_1$ and $f_2$ show below.

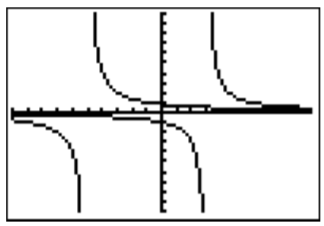
$clipboard_e0a6517e31b3e2b9580e4ce4e082b79a3.png$

As before, we recommend rewriting the inequality so that one side of the inequality becomes zero:

\[\begin{aligned} \dfrac{4}{x+5}<\dfrac{3}{x-3} & \implies \dfrac{4}{x+5}-\dfrac{3}{x-3} <0 \implies \quad \dfrac{4(x-3)-3(x+5)}{(x+5)(x-3)} <0 \\ & \implies \dfrac{4x-12-3x-15}{(x+5)(x-3)} <0 \implies \quad \dfrac{x-27}{(x+5)(x-3)}<0 \end{aligned} \nonumber \]

We therefore graph the function $f(x)=\dfrac{x-27}{(x+5)(x-3)}$.

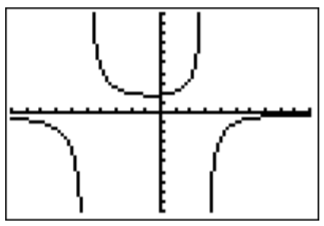
$clipboard_e52075872a51dc9e11d7661dec0ebf9d2.png$

The vertical asymptotes of $f(x)=\dfrac{x-27}{(x+5)(x-3)}$ are $x=-5$ and $x=3$. The $x$-intercept is $(27,0)$. We see from the graph that $f(x)<0$ for $x<-5$. To see the graph at $x>3$, we zoom to the $x$-intercept at $x=27$.

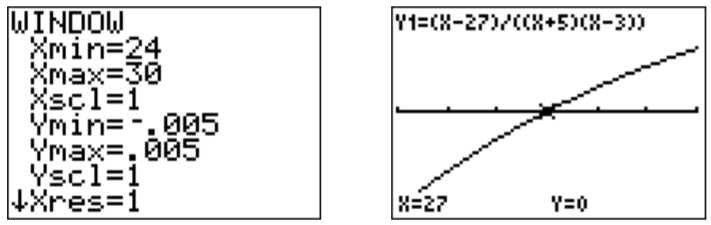
$clipboard_eb5d31816def294b8d857bf5b9ba3d608.png$

Therefore, the solution set is

\[\text{solution set}=\{x| x<-5,\text{ or } 3<x<27\}=(-\infty,-5)\cup (3,27) \nonumber \]

(The $x$-intercept $x=27$ is not included in the solution set since the original equation had a “$<$” and not “$\leq$” sign.)

To analyze $|2x-3|>7$, we graph the function $f(x)=|2x-3|-7$.

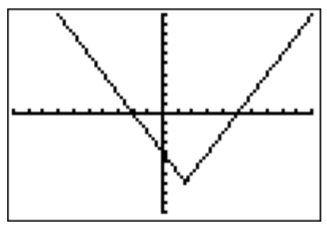
$clipboard_efc9dcd19d74a0fe7428de6f50bcb0dbd.png$

To see where $f(x)>0$, we find the zeros of $f(x)$.

\[|2x-3|-7=0 \implies \quad |2x-3|=7 \implies \quad 2x-3=\pm 7 \nonumber \]

\[\begin{aligned}
& \Longrightarrow 2 x-3=7 \\
(\text { add } 3) & \Longrightarrow 2 x=10 \\
(\text { divide by } 2) & \Longrightarrow x=5
\end{aligned} \quad \begin{aligned}
& \Longrightarrow 2 x-3=-7 \\
(\text { add } 3) & \Longrightarrow 2 x=-4 \\
(\text { divide by } 2) & \Longrightarrow x=-2
\end{aligned} \nonumber \]

\[\text{solution set}=(-\infty,-2)\cup(5,\infty) \nonumber \]

Search

Text Color

Text Size

Margin Size

Font Type