16.1: Half-life

Recall from definition Rate of Growth on page that a function with rate of growth $r$ is an exponential function $f(x)=c\cdot b^x$ with base $b=1+r$. There is also another important way of determining the base of an exponential function, which is given by the notion of half-life. We start with a motivating example. Consider the function $f(x)=200\cdot \left(\dfrac 1 2\right)^{\frac x 7}$. We calculate the function values $f(x)$, for $x=0$, $7$, $14$, $21$, and $28$.

$$\begin{aligned} f(0)&=200\cdot \left(\dfrac 1 2\right)^{\frac 0 7}= 200 \cdot 1=200\\ f(7)&=200\cdot \left(\dfrac 1 2\right)^{\frac 7 7}= 200 \cdot \dfrac 1 2=100\\ f(14)&=200\cdot \left(\dfrac 1 2\right)^{\frac {14} 7}= 200 \cdot \dfrac 1 4=50\\ f(21)&=200\cdot \left(\dfrac 1 2\right)^{\frac {21} 7}= 200 \cdot \dfrac 1 8=25\\ f(28)&=200\cdot \left(\dfrac 1 2\right)^{\frac {28} 7}= 200 \cdot \dfrac 1 {16}=12.5\\\end{aligned} \nonumber$$

From this calculation, we can see how the function values of $f$ behave: starting from $f(0)=200$, the function takes half of its value whenever $x$ is increased by $7$. For this reason, we say that $f$ has a half-life of $7$. (The general definition will be given below.) The graph of the function is displayed below.

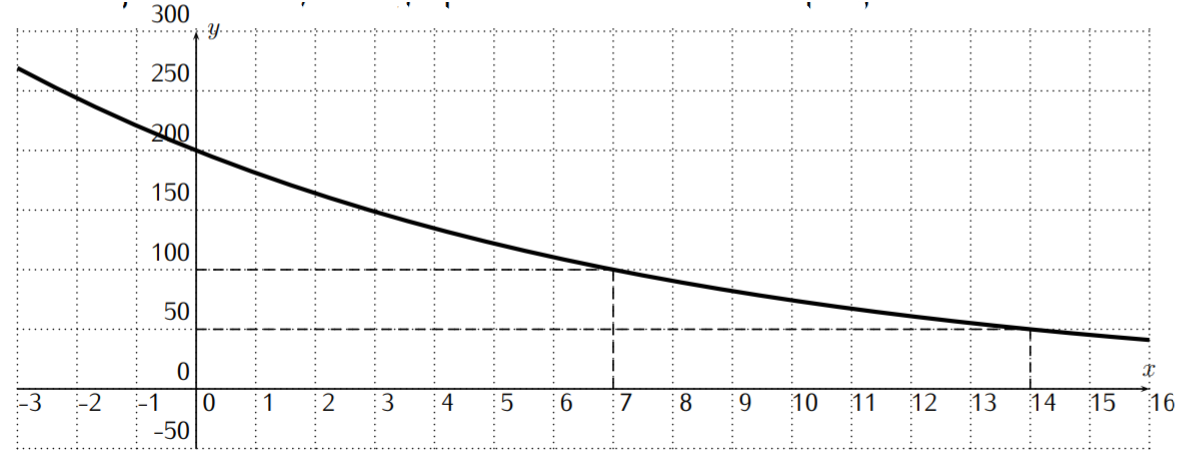
We collect the ideas that are displayed in the above example in the definition and observation below.

Definition: Half-Life

Let $f$ be an exponential function $f(x)=c\cdot b^x$ with a domain of all real numbers, $D=\mathbb{R}$. Then we say that $f$ has a half-life of $h$, if the base is given by

$$\label{half-life-base} \boxed{\,\, b=\left(\dfrac 1 2\right)^{\frac 1 h} \,\,}$$

Note that we can also write $h$ in terms of $b$. Converting $\ref{half-life-base}$ into a logarithmic equation gives $\dfrac 1 h = \log_{\frac 1 2} (b)=\dfrac{\log b}{\log \frac 1 2}$, so that $h=\dfrac{\log \frac 1 2}{\log{b}}=\log_b\left(\dfrac 1 2\right)$.

Let $f$ be the exponential function given for some real constants $c>0$ and half-life $h>0$, that is

$$f(x)=c\cdot \left(\left(\dfrac 1 2\right)^{\frac 1 h}\right)^x=c\cdot \left(\dfrac 1 2 \right)^{\frac x h} \nonumber$$

Then we can calculate $f(x+h)$ as follows:

$$\begin{aligned} f(x+h) &= c\cdot \left(\dfrac 1 2\right)^{\frac {x+h} h}=c\cdot \left(\dfrac 1 2\right)^{\frac x h+\frac h h}=c\cdot \left(\dfrac 1 2\right)^{\frac {x} h +1} \\ &=& c\cdot \left(\dfrac 1 2\right)^{\frac {x} h}\cdot \left(\dfrac 1 2\right)^1=\dfrac 1 2 \cdot f(x) \end{aligned} \nonumber$$

To summarize, $f$ has the following property:

$$\boxed{f(x+h)=\dfrac 1 2 f(x)} \quad\quad \text{for all }x \in \mathbb{R}.$$

The above equation shows that, whenever we add an amount of $h$ to an input $x$, the effect on $f$ is that the function value decreases by half its previous value. This is also displayed in the graph below.

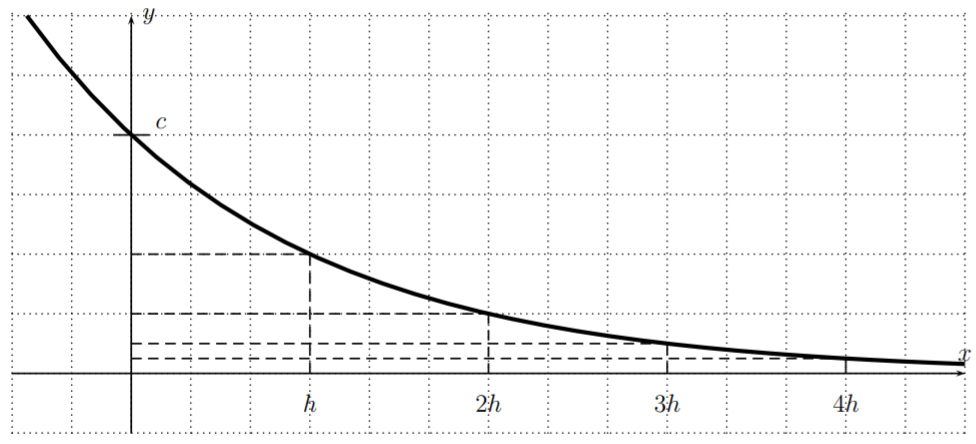
We will sometimes use a different letter for the input variable. In particular, the function $f(x)=c\cdot \left(\dfrac 1 2\right)^{\frac x h}$ is the same as the function $f(t)=c\cdot \left(\dfrac 1 2\right)^{\frac t h}$.

Example $\PageIndex{1}$

Many radioactive isotopes decay with well-known half-lives.

1. Chromium-51 has a half-life of $27.7$ days¹. How much of $3$ grams of chromium-51 will remain after $90$ days?
2. An isotope decays within $20$ hours from $5$ grams to $2.17$ grams. Find the half-life of the isotope.

Solution

1. We use the above formula $y=c\cdot \left(\dfrac 1 2\right)^{\frac t h}$, where $c=3$ grams is the initial amount of chromium-51, $h=27.7$ days is the half-life of chromium-51, and $t=90$ days is time that the isotope decayed. Substituting these numbers into the formula for $y$, we obtain:

$$y=3\cdot \left(\dfrac 1 2\right)^{\frac {90}{27.7}}\approx 0.316 \nonumber$$

Therefore, after $90$ days, $0.316$ grams of the chromium-51 is remaining.

2. We have an initial amount of $c=5$ grams and a remaining amount of $y=2.17$ grams after $t=20$ hours. The half-life can be obtained as follows.

$$\begin{aligned} 2.17&=5\cdot \left(\dfrac 1 2\right)^{\frac {20} {h}}\\ \implies 0.434&= \left(\dfrac 1 2\right)^{\frac {20} {h}} \quad \text{($\div 5$)}\\ \implies \ln(0.434)&= \ln\left(0.5^{\frac {20} h}\right) \quad \text{(apply $\ln$)}\\ \implies \ln(0.434)&= \dfrac {20} h\cdot \ln\left(0.5\right)\\ \implies h&=\dfrac{{20} \cdot \ln(0.5)}{\ln(0.434)} \quad \left(\times \dfrac{h}{\ln(0.434)}\right)\\ \implies t &\approx 16.6 \end{aligned} \nonumber$$

Therefore, the half-life of the isotope is approximately $16.6$ hours.

An important isotope is the radioisotope carbon-14. It decays with a half-life of $5730$ years with an accuracy of $\pm 40$ years. For definiteness we will take $5730$ years as the half-life of carbon-14.

$$\boxed{\text{The half-life of carbon-14 is $5730$ years.}}$$

One can use the knowledge of the half-life of carbon-14 in dating organic materials via the so called carbon dating method. Carbon-14 is produced by a plant during the process of photosynthesis at a fixed level until the plant dies. Therefore by measuring the remaining amount of carbon-14 in a dead plant one can determine the date when the plant died. Furthermore, since humans and animals consume plants, the same argument can be applied to determine their (approximate) dates of death.

Example $\PageIndex{2}$

1. A dead tree trunk has $86\%$ of its original carbon-14. (Approximately) how many years ago did the tree die?
2. A dead animal at an archeological site has lost $41.3\%$ of its carbon-14. When did the animal die?

Solution

1. Using the function $y=c\cdot \left(\dfrac 1 2\right)^{\frac t h}$, where $c$ is the amount of carbon-14 that was produced by the tree until it died, $y$ is the remaining amount to date, $t$ is the time that has passed since the tree has died, and $h$ is the half-life of carbon-14. Since $86\%$ of the carbon-14 is left, we have $y=86\%\cdot c$. Substituting the half-life $h=5730$ of carbon-14, we can solve for $t$.

$$\begin{aligned} 0.86\cdot c&=c\cdot \left(\dfrac 1 2\right)^{\frac t {5730}}\\ \implies 0.86&= \left(\dfrac 1 2\right)^{\frac t {5730}} \quad \text{($\div c$)}\\ \implies \ln(0.86)&= \ln\left(0.5^{\frac t {5730}}\right) \quad \text{(apply $\ln$)}\\ \ln(0.86)&= \dfrac t {5730}\cdot \ln\left(0.5\right)\\ \dfrac{5730}{\ln(0.5)}\cdot \ln(0.86)&=t \quad \left(\times \dfrac{5730}{\ln(0.5)}\right)\\ \implies t & \approx 1247 \end{aligned} \nonumber$$

Therefore, the tree died approximately $1247$ years ago.

2. Since $41.3\%$ of the carbon-14 is gone, $100\%-41.3\%=58.7\%$ is remaining. Using $y=c\cdot \left(\dfrac 1 2\right)^{\frac{t}{h}}$ with $y=58.7\%\cdot c$ and $h=5730$, we obtain

$$\begin{aligned} 0.587\cdot c&=c\cdot \left(\dfrac 1 2\right)^{\frac t {5730}}\\ \implies 0.587&= \left(\dfrac 1 2\right)^{\frac t {5730}} \quad \text{($\div c$)}\\ \implies \ln(0.587)&= \ln\left(0.5^{\dfrac t {5730}}\right) \quad \text{(apply $\ln$)}\\ \implies \ln(0.587)&= \dfrac t {5730}\cdot \ln\left(0.5\right)\\ \dfrac{5730}{\ln(0.5)}\cdot \ln(0.587)&=t \quad \left(\times \dfrac{5730}{\ln(0.5)} \right)\\ t &\approx 4404 \end{aligned} \nonumber$$

The animal died $4404$ years ago.

References

1. Half-lives are taken from: https://en.Wikipedia.org/wiki/List_o...fe#100_seconds