18.1: Addition and subtraction of angles
- Page ID
- 49066
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the previous section we found exact values of the trigonometric functions for specific angles of \(0, \dfrac{\pi}{3}, \dfrac{\pi}{4}, \dfrac{\pi}{6}\) plus possibly any multiple of \(\dfrac{\pi}{2}\). Using these values, we can find many other values of trigonometric functions via the following addition and subtraction of angles formulas, which we state now.
For any angles \(\alpha\) and \(\beta\), we have:
\[\begin{aligned}
\sin (\alpha+\beta) &=\sin \alpha \cos \beta+\cos \alpha \sin \beta \\
\sin (\alpha-\beta) &=\sin \alpha \cos \beta-\cos \alpha \sin \beta \\
\cos (\alpha+\beta) &=\cos \alpha \cos \beta-\sin \alpha \sin \beta \\
\cos (\alpha-\beta) &=\cos \alpha \cos \beta+\sin \alpha \sin \beta \\
\tan (\alpha+\beta) &=\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\
\tan (\alpha-\beta) &=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}
\end{aligned} \nonumber \]
- Proof
-
We start with the proof of the formulas for \(\sin(\alpha+\beta)\) and \(\cos(\alpha+\beta)\) when \(\alpha\) and \(\beta\) are angles between \(0\) and \(\dfrac \pi 2=90^\circ\). We prove the addition formulas (for \(\alpha,\beta\in \left (0,\dfrac \pi 2\right)\)) in a quite elementary way, and then show that the addition formulas also hold for arbitrary angles \(\alpha\) and \(\beta\).
To find \(\sin(\alpha+\beta)\), consider the following setup.
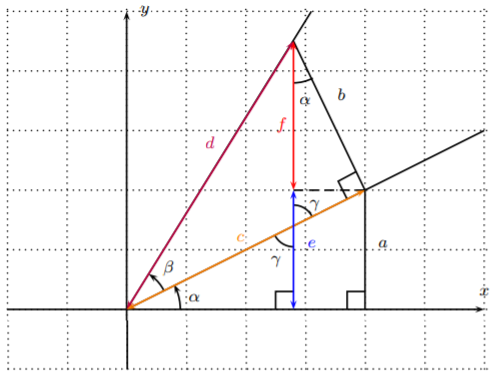
Note, that there are vertically opposite angles, labelled by \(\gamma\), which are therefore equal. These angles are angles in two right triangles, with the third angle being \(\alpha\). We therefore see that the angle \(\alpha\) appears again as the angle among the sides \(b\) and \(f\). With this, we can now calculate \(\sin(\alpha+\beta)\).
\[\begin{aligned} \sin(\alpha+\beta)&=\dfrac{\text{opposite}}{\text{hypotenuse}}=\dfrac{e+f}{d}=\dfrac{e}{d}+\dfrac{f}{d}=\dfrac{a}{d}+\dfrac{f}{d}=\dfrac{a}{c}\cdot \dfrac{c}{d}+\dfrac{f}{b}\cdot \dfrac{b}{d}\\ &=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)\end{aligned} \nonumber \]
The above figure displays the situation when \(\alpha+\beta\leq \dfrac \pi 2\). There is a similar figure for \(\dfrac \pi 2< \alpha+\beta<\pi\). (We recommend as an exercise to draw the corresponding figure for the case of \(\dfrac \pi 2< \alpha+\beta<\pi\).)
Next, we prove the addition formula for \(\cos(\alpha+\beta)\). The following figure depicts the relevant objects.
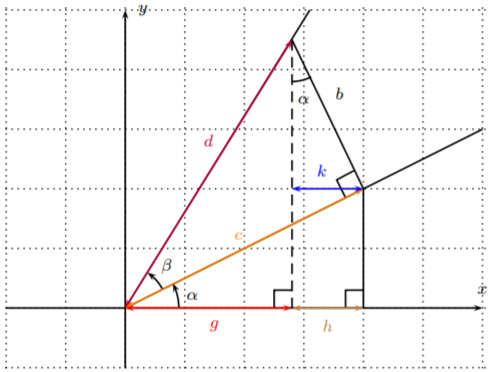
We calculate \(\cos(\alpha+\beta)\) as follows.
\[\begin{aligned} \cos(\alpha+\beta)&=\dfrac{\text{adjacent}}{\text{hypotenuse}}=\dfrac{g}{d}=\dfrac{g+h}{d}-\dfrac{h}{d}=\dfrac{g+h}{d}-\dfrac{k}{d}=\dfrac{g+h}{c}\cdot \dfrac{c}{d}-\dfrac{k}{b}\cdot \dfrac{b}{d}\\ &=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\end{aligned} \nonumber \]
Again, there is a corresponding figure when the angle \(\alpha+\beta\) is greater than \(\dfrac \pi 2\). (We encourage the student to check the addition formula for this situation as well.)
We therefore have proved the addition formulas for \(\sin(\alpha+\beta)\) and \(\cos(\alpha+\beta)\) when \(\alpha\) and \(\beta\) are angles between \(0\) and \(\dfrac \pi 2\), which we will now extend to all angles \(\alpha\) and \(\beta\). First, note that the addition formulas are trivially true when \(\alpha\) or \(\beta\) are \(0\). (Check this!) Now, by observing that \(\sin(x)\) and \(\cos(x)\) can be converted to each other via shifts of \(\dfrac \pi 2\), (or, alternatively, by using the identities [EQU:basic-trig-eqns-wrt-pi] and [EQ:cos=sin+pi2]), we obtain, that
\[\begin{aligned} \sin\left (x+\dfrac \pi 2 \right)=\,\,\,\,\,\cos x, && \cos\left (x+\dfrac \pi 2 \right) = -\sin(x), \\ \sin\left (x-\dfrac \pi 2\right)=-\cos x, && \cos\left(x-\dfrac \pi 2 \right) = \,\,\,\,\,\sin(x). \end{aligned} \nonumber \]
With this, we extend the addition identities for \(\alpha\) by \(\pm \dfrac \pi 2\) as follows:
\[\begin{aligned} \sin\left(\left(\alpha+\dfrac \pi 2\right)+\beta\right)&= \sin\left(\alpha+\beta+\dfrac \pi 2\right)=\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta) \\ &= \sin\left(\alpha+\dfrac \pi 2\right)\cos(\beta)+\cos\left(\alpha+\dfrac \pi 2\right)\sin(\beta) \\ \sin\left(\left(\alpha-\dfrac \pi 2\right)+\beta\right)&= \sin\left(\alpha+\beta-\dfrac \pi 2\right)=-\cos(\alpha+\beta)=-\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta) \\ &= \sin\left(\alpha-\dfrac \pi 2\right)\cos(\beta)+\cos\left(\alpha-\dfrac \pi 2\right)\sin(\beta) \\ \cos\left(\left(\alpha+\dfrac \pi 2\right)+\beta\right)&= \cos\left(\alpha+\beta+\dfrac \pi 2\right)=-\sin(\alpha+\beta)=-\sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta) \\ &= \cos\left(\alpha+\dfrac \pi 2\right)\cos(\beta)-\sin\left(\alpha+\dfrac \pi 2\right)\sin(\beta) \\ \cos\left(\left(\alpha-\dfrac \pi 2\right)+\beta\right)&= \cos\left(\alpha+\beta-\dfrac \pi 2\right)=\sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta) \\ &= \cos\left(\alpha-\dfrac \pi 2\right)\cos(\beta)-\sin\left(\alpha-\dfrac \pi 2\right)\sin(\beta)\end{aligned} \nonumber \]
There are similar proofs to extend the identities for \(\beta\). An induction argument shows the validity of the addition formulas for arbitrary angles \(\alpha\) and \(\beta\).
The remaining formulas now follow via the use of trigonometric identities.
\[\tan(\alpha+\beta)=\dfrac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\dfrac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}=\dfrac{\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\frac{\cos\alpha\cos\beta-\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}=\dfrac{\frac{\sin\alpha}{\cos\alpha}+\frac{\sin\beta}{\cos\beta}}{1-\frac{\sin\alpha}{\cos\alpha}\frac{\sin\beta}{\cos\beta}} \nonumber \]
This shows that \(\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\). For the relations with \(\alpha-\beta\), we use the fact that \(\sin\) and \(\tan\) are odd functions, whereas \(\cos\) is an even function, see identities [EQ:sin-odd-cos-even] and [EQ:tan-odd].
\[\begin{aligned} \sin(\alpha-\beta)&=\sin(\alpha+(-\beta))=\sin(\alpha)\cos(-\beta)+\cos(\alpha)\sin(-\beta) =\sin\alpha\cos\beta-\cos\alpha\sin\beta \\ \cos(\alpha-\beta)&=\cos(\alpha+(-\beta))=\cos(\alpha)\cos(-\beta)-\sin(\alpha)\sin(-\beta)= \cos\alpha\cos\beta+\sin\alpha\sin\beta \\ \tan(\alpha-\beta)&=\tan(\alpha+(-\beta))=\dfrac{\tan(\alpha)+\tan(-\beta)}{1-\tan(\alpha)\tan(-\beta)}=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{aligned} \nonumber \]
This completes the proof of the proposition.
Before giving examples of the above proposition, we recall the elementary function values of the \(\sin\), \(\cos\), and \(\tan\) from the previous section:
\[\begin{array}{c||c|c|c|c|c|c}
x & 0=0^{\circ} & \dfrac{\pi}{6}=30^{\circ} & \dfrac{\pi}{4}=45^{\circ} & \dfrac{\pi}{3}=60^{\circ} & \dfrac{\pi}{2}=90^{\circ} & \pi=180^{\circ} \\
\hline \hline \sin (x) & 0 & \dfrac{1}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & 1 & 0 \\
\hline \cos (x) & 1 & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 & -1 \\
\hline \tan (x) & 0 & \dfrac{\sqrt{3}}{3} & 1 & \sqrt{3} & \text { undef. } & 0
\end{array} \nonumber \]
Find the exact values of the trigonometric functions.
- \(\cos\left(\dfrac{\pi}{12}\right)\)
- \(\tan\left(\dfrac{5\pi}{12}\right)\)
- \(\cos\left(\dfrac{11\pi}{12}\right)\)
Solution
- The key is to realize the angle \(\dfrac{\pi}{12}\) as a sum or difference of angles with known trigonometric function values. Note, that \(\dfrac{\pi}{3}-\dfrac{\pi}{4}=\dfrac{4\pi-3\pi}{12}=\dfrac{\pi}{12}\), so that
\[\begin{aligned}
\cos\left(\dfrac{\pi}{12}\right) &= \cos\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)\\
&= \cos\dfrac{\pi}{3}\cos\dfrac{\pi}{4}+\sin\dfrac{\pi}{3}\sin\dfrac{\pi}{4}\\
&= \dfrac{1}{2}\cdot \dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{2}}{2}\\
&= \dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4}\\
&= \dfrac{\sqrt{2}+\sqrt{6}}{4}
\end{aligned} \nonumber \]
We remark that the last expression is in the simplest form and cannot be simplified any further.
- Again we can write the angle \(\dfrac{5\pi}{12}\) as a sum involving only special angles given in the table above: \(\dfrac{5\pi}{12}=\dfrac{2\pi}{12}+\dfrac{3\pi}{12}=\dfrac{\pi}{6}+\dfrac{\pi}{4}\). Therefore,
\[\begin{aligned}
\tan\left(\dfrac{5\pi}{12}\right)&= \tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)\\
&= \dfrac{\tan\frac{\pi}{6}+\tan\frac{\pi}{4}}{1-\tan\frac{\pi}{6}\tan\frac{\pi}{4}}\\
&= \dfrac{\frac{\sqrt{3}}{3}+1}{1-\frac{\sqrt{3}}{3}\cdot 1} \\
&= \dfrac{\frac{\sqrt{3}+3}{3}}{\frac{3-\sqrt{3}}{3}}\\
&= \dfrac{\sqrt{3}+3}{3}\cdot \dfrac{3}{3-\sqrt{3}}\\
&= \dfrac{\sqrt{3}+3}{3-\sqrt{3}} \\
&\approx 3.732
\end{aligned} \nonumber \]
Here, we may simplify the last expression further by rationalizing the denominator. This is done by multiplying \((3+\sqrt{3})\) to numerator and denominator.
\[\begin{aligned}
\tan\left(\dfrac{5\pi}{12}\right)&= \dfrac{(\sqrt{3}+3)\cdot (3+\sqrt{3})}{(3-\sqrt{3})\cdot (3+\sqrt{3})}\\
&= \dfrac{3\sqrt{3}+\sqrt{3}^2+9+3\sqrt{3}}{3^2-\sqrt{3}^2} \\
&= \dfrac{3+9+6\sqrt{3}}{9-3}\\
&= \dfrac{12+6\sqrt{3}}{6}\\
&= 2+\sqrt{3}\\
&\approx 3.732
\end{aligned} \nonumber \]
- Again we need to write the angle \(\dfrac{11\pi}{12}\) as a sum or difference of the above angles. In fact, we can do so in at least two different ways: \(\dfrac{11\pi}{12}=\dfrac{6\pi}{12}+\dfrac{5\pi}{12}\) and also \(\dfrac{11\pi}{12}=\dfrac{12\pi}{12}-\dfrac{\pi}{12}=\pi-\dfrac{\pi}{12}\). In either case, we first need to calculate some other trigonometric functions, namely those for either \(\dfrac{5\pi}{12}\) or \(\dfrac{\pi}{12}\). We choose the second solution, and using part (a), we have
\[\cos\left(\dfrac{\pi}{12}\right) = \dfrac{\sqrt{2}+\sqrt{6}}{4}\nonumber \]
and
\[\begin{aligned}
\sin\left(\dfrac{\pi}{12}\right)&= \sin\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)\\
&=\sin\dfrac{\pi}{3}\cos\dfrac{\pi}{4}-\cos\dfrac{\pi}{3}\sin\dfrac{\pi}{4} \\
&= \dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\cdot \dfrac{\sqrt{2}}{2}\\
&=\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\
&=\dfrac{\sqrt{6}-\sqrt{2}}{4}
\end{aligned} \nonumber \]
With this, we have
\[\begin{aligned}
\cos\left(\dfrac{11\pi}{12}\right) &= \cos\left(\pi-\dfrac{\pi}{12}\right)\\
&=\cos\pi\cos\dfrac{\pi}{12}+\sin\pi\sin\dfrac{\pi}{12} \\
&= (-1)\cdot \dfrac{\sqrt{2}+\sqrt{6}}{4}+0\cdot \dfrac{\sqrt{6}-\sqrt{2}}{4}\\
&=\dfrac{-(\sqrt{2}+\sqrt{6})}{4}\\
&\approx 0.9569
\end{aligned} \nonumber \]
Generalizing the previous example, we can obtain any multiple of \(\dfrac{\pi}{12}\) as a sum or difference of known angles coming from the \(30^\circ-60^\circ-90^\circ\) and \(45^\circ-45^\circ-90^\circ\) triangles.
Starting from the angles \(\dfrac{\pi}{6}=\dfrac{2\pi}{12}\), \(\dfrac{\pi}{4}=\dfrac{3\pi}{12}\), \(\dfrac{\pi}{3}=\dfrac{4\pi}{12}\), and \(\dfrac{\pi}{2}=\dfrac{6\pi}{12}\), we obtain multiples of the angle \(\dfrac{\pi}{12}\) by addition and subtraction, such as:
\[\begin{aligned}
\dfrac{\pi}{12}&=\dfrac{4 \pi}{12}-\dfrac{3 \pi}{12},\\
\dfrac{5 \pi}{12}&=\dfrac{2 \pi}{12}+\dfrac{3 \pi}{12},\\
\dfrac{7 \pi}{12}&=\dfrac{4 \pi}{12}+\dfrac{3 \pi}{12},\\
\dfrac{8 \pi}{12}&=\dfrac{4 \pi}{12}+\dfrac{4 \pi}{12},\\
\dfrac{9 \pi}{12}&=\dfrac{6 \pi}{12}+\dfrac{3 \pi}{12},\\
\dfrac{10 \pi}{12}&=\dfrac{6 \pi}{12}+\dfrac{4 \pi}{12},\\
\dfrac{11 \pi}{12}&=\dfrac{6 \pi}{12}+\dfrac{5 \pi}{12}=\dfrac{12 \pi}{12}-\dfrac{\pi}{12}
\end{aligned} \nonumber \]
Here, the trigonometric function values of the last fraction is obtained from the previously obtained trigonometric values, as in part (c) of example \(\PageIndex{1}\) above. Higher multiples of \(\dfrac{\pi}{12}\) can be obtained from the above list by adding multiples of \(\pi\) to it. Note also that in many instances there are several ways of writing an angle as a sum or difference. For example: \(\dfrac{8\pi}{12}=\dfrac{4\pi}{12}+\dfrac{4\pi}{12}=\dfrac{6\pi}{12}+\dfrac{2\pi}{12}=\dfrac{12\pi}{12}-\dfrac{4\pi}{12}\)
Using proposition [PROP:trig-add-subt-formulas] we can prove other related trigonometric identities with the addition and subtraction formulas. We rewrite \(\cos\left(x+\dfrac{\pi}{2}\right)\) by using the subtraction formula.
Solution
\[\cos\left(x+\dfrac{\pi}{2}\right) = \cos x\cdot \cos\dfrac{\pi}{2}-\sin x\cdot \sin\dfrac{\pi}{2} = \cos x\cdot 0+\sin x\cdot 1=\sin(x) \nonumber \]


