19.1: The functions of arcsin, arccos, and arctan

The inverse trigonometric functions are the inverse functions of the $y=\sin x$, $y=\cos x$, and $y=\tan x$ functions restricted to appropriate domains. In this section we give a precise definition of these functions.

The Inverse Tangent Function

We start with the inverse to the tangent function $y=\tan(x)$. Recall that the graph of $y=\tan(x)$ is the following:

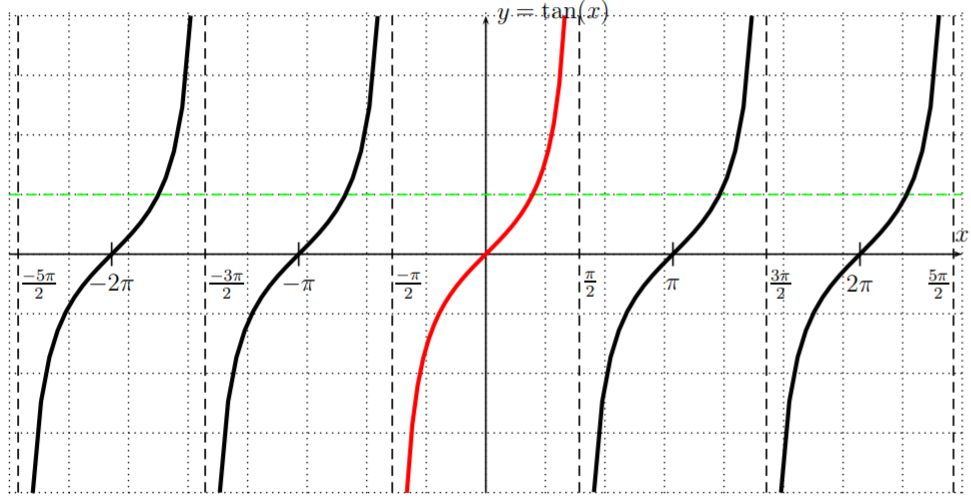
It has vertical asymptotes at $x=\pm\dfrac{\pi}{2}, \pm\dfrac{3\pi}{2}, \pm\dfrac{5\pi}{2}, \dots$. Note, that $y=\tan(x)$ is not a one-to-one function in the sense of defintion [DEF:1-to-1] on page . (For example, the horizontal line $y=1$ intersects the graph at $x=\dfrac{\pi}{4}$, $x=\dfrac{\pi}{4}\pm\pi$, $x=\dfrac{\pi}{4}\pm2\pi$, etc.) However, when we restrict the function to the domain $D=(\dfrac{-\pi}{2},\dfrac{\pi}{2})$ the restricted function is one-to-one, and, for this restricted function, we may take its inverse function.

Definition: Inverse Tangent or Arctangent

The inverse of the function $y=\tan(x)$ with restricted domain $D=(\dfrac{-\pi}{2},\dfrac{\pi}{2})$ and range $R=\mathbb{R}$ is called the inverse tangent or arctangent function. It is denoted by

$$y=\tan^{-1}(x) \quad \text{ or } \quad y= \arctan(x) \quad \iff \quad \tan(y)=x, \quad y\in\left(-\dfrac{\pi}2,\dfrac{\pi}{2}\right) \nonumber$$

The arctangent reverses the input and output of the tangent function, so that the arctangent has domain $D=\mathbb{R}$ and range $R=\left(\dfrac{-\pi}{2},\dfrac{\pi}{2}\right)$. The graph is displayed below.

Warning

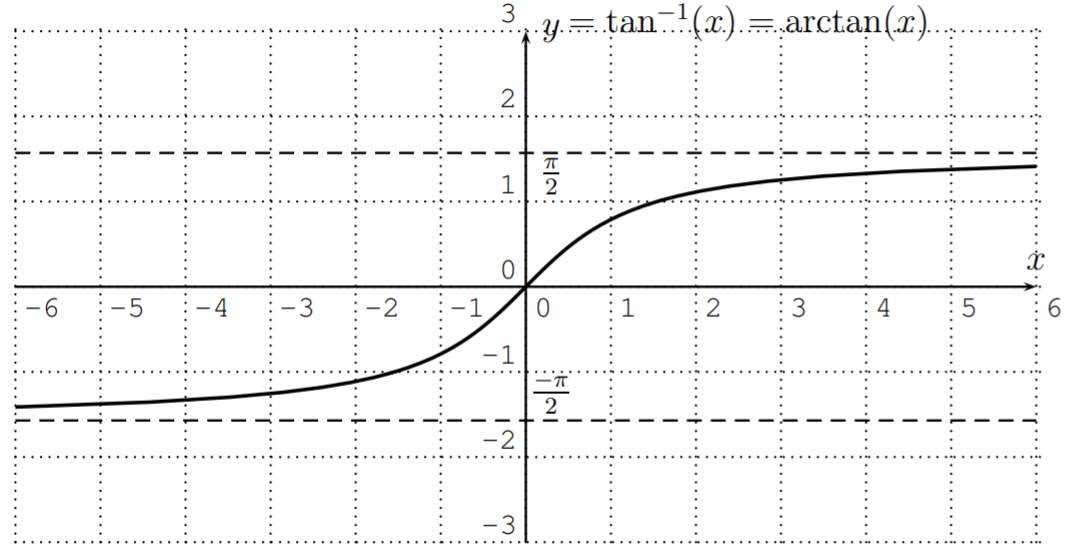
The notation of $\tan^{-1}(x)$ and $\tan^2(x)$ is slightly inconsistent, since the exponentiation symbol is used above in two different ways. In fact, $\tan^{-1}(x)=\arctan(x)$ refers to the inverse function of the $\tan(x)$ function. However, when we write $\tan^2(x)$, we mean

$$\tan^2(x)=(\tan(x))^2=\tan(x)\cdot \tan(x) \nonumber$$

Therefore, $\tan^{-1}(x)$ is the inverse function of $\tan(x)$ with respect to the composition operation, whereas $\tan^2(x)$ is the square with respect to the usual product in $\mathbb{R}$. Note also that the inverse function of the tangent with respect to the product in $\mathbb{R}$ is $y=\dfrac{1}{\tan(x)}=\cot(x)$, which is the cotangent.

Observation: Inverse Tangent Function

The inverse tangent function is an odd function:

$$\label{EQU:tan-1(-x)} \boxed{\tan^{-1}(-x)=-\tan^{-1}(x)} \nonumber$$

This can be seen by observing that the tangent $y=\tan(x)$ is an odd function (that is $\tan(-x)=-\tan(x)$), or directly from the symmetry of the graph with respect to the origin $(0,0)$.

The next example calculates function values of the inverse tangent function.

Example $\PageIndex{1}$

Recall the exact values of the tangent function from section 17.1:

$$\begin{array}{c||c|c|c|c|c} x & 0=0^{\circ} & \dfrac{\pi}{6}=30^{\circ} & \dfrac{\pi}{4}=45^{\circ} & \dfrac{\pi}{3}=60^{\circ} & \dfrac{\pi}{2}=90^{\circ} \\ \hline \hline \tan (x) & 0 & \dfrac{\sqrt{3}}{3} & 1 & \sqrt{3} & \text { undef. } \end{array} \nonumber$$

Solution

From this, we can deduce function values by reversing inputs and outputs, such as:

$$\begin{aligned} \tan\Big(\dfrac{\pi}{6}\Big)=\dfrac{\sqrt{3}}{3} &\implies & \tan^{-1}\Big(\dfrac{\sqrt{3}}{3} \Big)=\dfrac{\pi}{6} \\ \tan\Big(\dfrac{\pi}{4}\Big)=1 &\implies & \tan^{-1}\big(1 \big)=\dfrac{\pi}{4} \end{aligned} \nonumber$$

Also, since $\tan^{-1}(-x)=-\tan^{-1}(x)$, we obtain the inverse tangent of negative numbers.

$$\begin{aligned} \tan^{-1}(-\sqrt{3})&=&-\tan^{-1}(\sqrt{3})=-\dfrac{\pi}{3} \\ \tan^{-1}(-1)&=&-\tan^{-1}(1)=-\dfrac{\pi}{4} \end{aligned} \nonumber$$

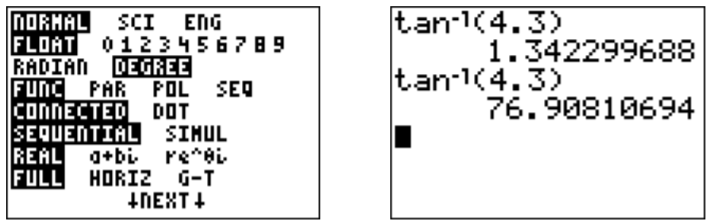
We may calculate the inverse tangent of specific values with the calculator using the $\boxed {\text{2nd}}$ and $\boxed {\text{tan}}$ keys. For example, $\tan^{-1}(4.3)\approx 1.34$.

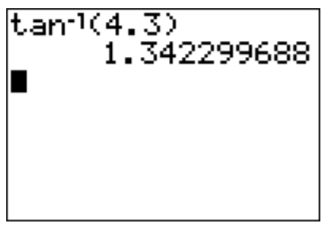
Note, that the answer differs, when changing the mode from radians to degree, since $\tan^{-1}(4.3) \approx 76.9^\circ \approx 1.34$.

The function $y=\sin^{-1}(x)$

Next, we define the inverse sine function. For this, we again first recall the graph of the $y=\sin(x)$ function, and note that it is also not one-to-one.

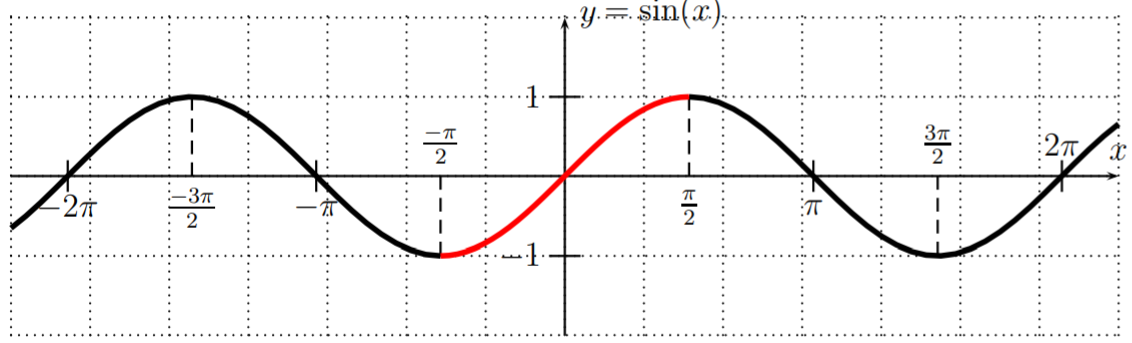
However, when restricting the sine to the domain $\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]$, the restricted function is one-to-one. Note furthermore, that when restricting the domain to $\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]$, the range is $[-1,1]$, and therefore we cannot extend this to a larger domain in a way such that the function remains a one-to-one function. We use the domain $\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]$ to define the inverse sine function.

Definition: Inverse Sine or Arcsine

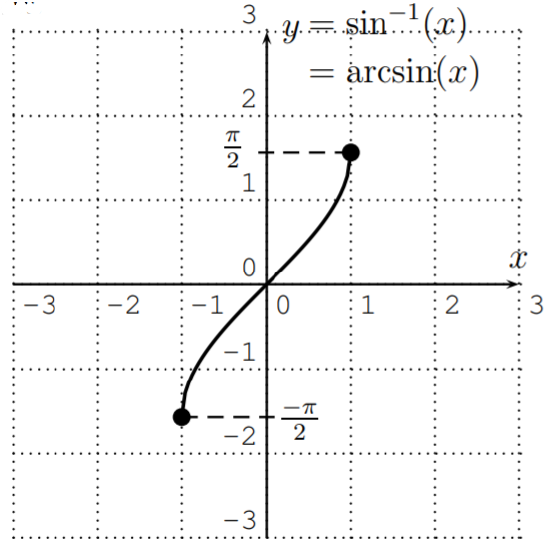
The inverse of the function $y=\sin(x)$ with restricted domain $D=\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]$ and range $R=[-1,1]$ is called the inverse sine or arcsine function. It is denoted by

$$y=\sin^{-1}(x) \quad \text{ or } \quad y= \arcsin(x) \quad \iff \quad \sin(y)=x, \quad y\in\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right] \nonumber$$

The arcsine reverses the input and output of the sine function, so that the arcsine has domain $D=[-1,1]$ and range $R=\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]$. The graph of the arcsine is drawn below.

Observation: Inverse Tangent Function

The inverse sine function is odd:

$$\label{EQU:sin-1(-x)} \boxed{\sin^{-1}(-x)=-\sin^{-1}(x)} \nonumber$$

This can again be seen by observing that the sine $y=\sin(x)$ is an odd function (that is $\sin(-x)=-\sin(x)$), or alternatively directly from the symmetry of the graph with respect to the origin $(0,0)$.

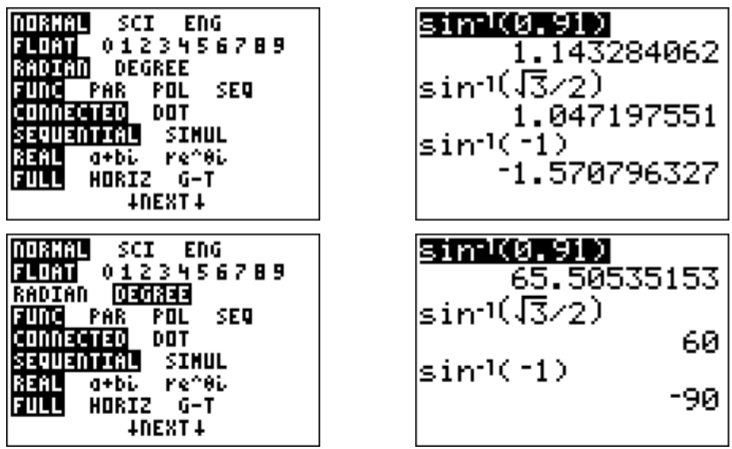
We now calculate specific function values of the inverse sine.

Example $\PageIndex{2}$

We first recall the known values of the sine.

$$\begin{array}{c||c|c|c|c|c} x & 0=0^{\circ} & \dfrac{\pi}{6}=30^{\circ} & \dfrac{\pi}{4}=45^{\circ} & \dfrac{\pi}{3}=60^{\circ} & \dfrac{\pi}{2}=90^{\circ} \\ \hline \hline \sin (x) & 0 & \dfrac{1}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & 1 \end{array} \nonumber$$

Solution

These values together with the fact that the inverse sine is odd, that is $\sin^{-1}(-x)=-\sin^{-1}(x)$, provides us with examples of its function values.

$$\begin{aligned} \sin^{-1}\Big(\dfrac{\sqrt{2}}{2}\Big) &= \dfrac{\pi}{4}\\\sin^{-1}(1) &=\dfrac{\pi}{2}\\ \sin^{-1}(0) &= 0\\\sin^{-1}\Big(\dfrac{-1}{2}\Big) &=-\sin^{-1}\Big(\dfrac{1}{2}\Big)=-\dfrac{\pi}{6}\end{aligned} \nonumber$$

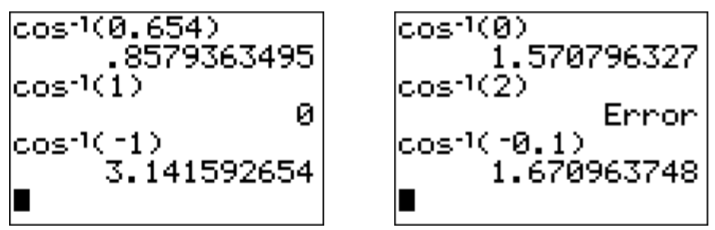
Note, that the domain of $y=\sin^{-1}(x)$ is $D=[-1,1]$, so that input numbers that are not in this interval give undefined outputs of the inverse sine:

$$\sin^{-1}(3) \text{ is undefined} \nonumber$$

Input values that are not in the above table may be found with the calculator via the $\boxed {\text{2nd}}$$\boxed {\text{sin}}$ keys. We point out, that the output values depend on wether the calculator is set to radian or degree mode. (Recall that the $\boxed {\text{mode}}$ may be changed via the key).

The function $y=\cos^{-1}(x)$

Finally, we define the inverse cosine. Recall the graph of $y=\cos(x)$, and note again that the function is not one-to-one.

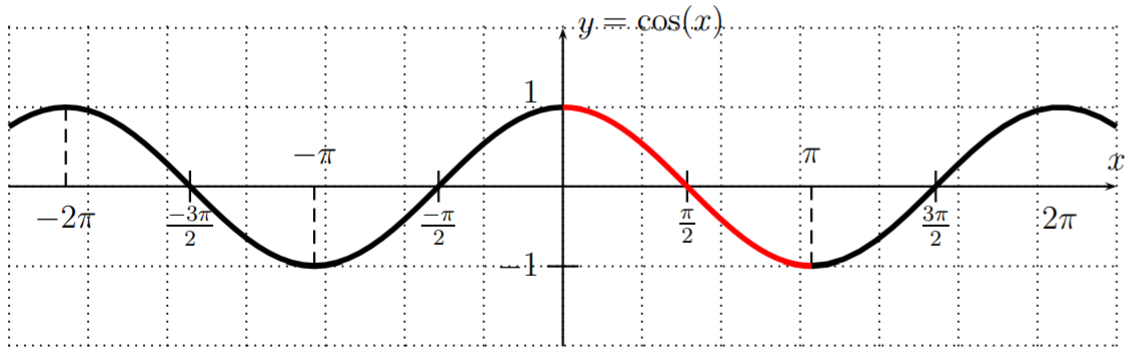
In this case, the way to restrict the cosine to a one-to-one function is not as clear as in the previous cases for the sine and tangent. By convention, the cosine is restricted to the domain $[0,\pi]$. This provides a function that is one-to-one, which is used to define the inverse cosine.

Definition: Inverse Cosine or Arccosine

The inverse of the function $y=\cos(x)$ with restricted domain $D=[0,\pi]$ and range $R=[-1,1]$ is called the inverse cosine or arccosine function. It is denoted by

$$y=\cos^{-1}(x) \quad \text{ or } \quad y= \arccos(x) \quad \iff \quad \cos(y)=x,\quad y\in [0,\pi] \nonumber$$

The arccosine reverses the input and output of the cosine function, so that the arccosine has domain $D=[-1,1]$ and range $R=[0,\pi]$. The graph of the arccosine is drawn below.

Observation: Inverse Cosine

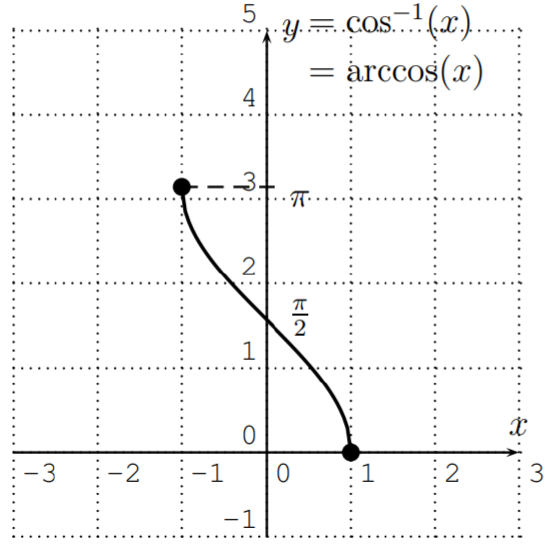
The inverse cosine function is neither even nor odd. That is, the function $\cos^{-1}(-x)$ cannot be computed by simply taking $\pm\cos^{-1}(x)$. But it does have some symmetry given algebraically by the more complicated relation

$$\label{EQU:cos-1(-x)} \boxed{\cos^{-1}(-x)=\pi-\cos^{-1}(x)} \nonumber$$

Proof

We can see that if we shift the graph down by $\dfrac{\pi}{2}$ the resulting function is odd. That is to say the function with the rule $\cos^{-1}(x)-\dfrac{\pi}{2}$ is odd:

$$\cos^{-1}(-x)-\dfrac{\pi}{2}=-(\cos^{-1}(x)-\dfrac{\pi}{2}) \nonumber$$

which yields $\ref{EQU:cos-1(-x)}$ upon distributing and adding $\dfrac{\pi}{2}$.

Another, more formal approach is as follows. The bottom right relation of [EQU:basic-trig-eqns-wrt-pi] on page states, that we have the relation $\cos(\pi-y)=-\cos(y)$ for all $y$. Let $-1\leq x\leq 1$, and denote by $y=\cos^{-1}(x)$. That is $y$ is the number $0\leq y\leq \pi$ with $\cos(y)=x$. Then we have

$-x=-\cos(y)=\cos(\pi-y)$ (by equation 17.1.2)

Applying $\cos^{-1}$ to both sides gives:

$$\cos^{-1}(-x)=\cos^{-1}(\cos(\pi-y))=\pi-y \nonumber$$

The last equality follows, since $\cos$ and $\cos^{-1}$ are inverse to each other, and $0\leq y\leq \pi$, so that $0\leq \pi-y\leq \pi$ are also in the range of the $\cos^{-1}$. Rewriting $y=\cos^{-1}(x)$ gives the wanted result:

$$\cos^{-1}(-x)=\pi-\cos^{-1}(x) \nonumber$$

This is the equation $\ref{EQU:cos-1(-x)}$ which we wanted to prove.

We now calculate specific function values of the inverse cosine.

Example $\PageIndex{3}$

We first recall the known values of the cosine.

$$\begin{array}{c||c|c|c|c|c} x & 0=0^{\circ} & \dfrac{\pi}{6}=30^{\circ} & \dfrac{\pi}{4}=45^{\circ} & \dfrac{\pi}{3}=60^{\circ} & \dfrac{\pi}{2}=90^{\circ} \\ \hline \hline \cos (x) & 1 & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 \end{array} \nonumber$$

Solution

Here are some examples for function values of the inverse cosine.

$$\cos^{-1}\Big(\dfrac{\sqrt{3}}{2}\Big)=\dfrac{\pi}{6}, \quad\quad \cos^{-1}(1)=0,\quad\quad \cos^{-1}(0) =\dfrac{\pi}{2} \nonumber$$

Negative inputs to the arccosine can be calculated with equation $\ref{EQU:cos-1(-x)}$, that is $\cos^{-1}(-x)=\pi-\cos^{-1}(x)$, or by going back to the unit circle definition.

$$\begin{aligned} \cos^{-1}\Big(-\dfrac{1}{2}\Big)&=\pi-\cos^{-1}\Big(\dfrac{1}{2}\Big)=\pi-\dfrac{\pi}{3}=\dfrac{3\pi-\pi}{3}=\dfrac{2\pi}{3}\\ \cos^{-1}(-1)&=\pi-\cos^{-1}(1)=\pi-0=\pi\end{aligned} \nonumber$$

Furthermore, the domain of $y=\cos^{-1}(x)$ is $D=[-1,1]$, so that input numbers not in this interval give undefined outputs of the inverse cosine.

$$\cos^{-1}(17) \text{ is undefined} \nonumber$$

Other input values can be obtained with the calculator by pressing the $\boxed {\text{2nd}}$$\boxed {\text{cos}}$ keys. For example, we obtain the following function values (here using radian measure).