3.2: Technology and Right Triangle Trigonometry

Suggested Prerequisite Topics

This section is designed assuming you understand the following topics from Algebra.

• Unit analysis and conversion
• Inverse Functions
  • Basic definition
  • notation of an inverse

Learning Objectives

• Use a calculator to approximate the value of a trigonometric function.
• Perform addition and subtraction on angles expressed in DMS.
• Convert between DMS form and DD form.
• Use a calculator to approximate an acute angle given the value of a trigonometric function.

Using a Calculator to Compute the Values of Trigonometric Functions

The trigonometric values for non-special angles were originally collected into tables and are available on scientific calculators (and other, more recent, technology). For example, let's find the sine of \(50^{\circ}\).

Note: Change to Degree Mode

Before evaluating any trigonometric function, ensure your technology is set to the correct "mode." In Trigonometry, the two standard modes are degree mode and radian mode. At this point, we will only be working with angles measured in degrees, so you must only concern yourself with degree mode. If using a scientific or graphing calculator, refer to your instruction manual on setting the calculator to degree mode. The scientific calculator in Desmos is set to degree mode by default, so you do not have to make any adjustments if using that technology; however, the graphing calculator in Desmos defaults to radian mode. To change Desmos' graphing calculator to degree mode, open the "Graph Settings" and select "Degrees."

Example \( \PageIndex{ 1 } \)

Approximate \( \sin\left( 50^{ \circ } \right) \).

Scientific and Graphing Calculators

Press the \( \mathrm{SIN} \) button. Your calculator will display\[\sin (\nonumber \]with an open parenthesis as the prompt to enter an angle. Type \(50\) and press \( \mathrm{ENTER} \) (since your calculator should already be in degree mode, it will interpret the \( 50 \) as \( 50^{ \circ } \)). The calculator returns \(0.7660444431\) (please verify).

Desmos

Using the scientific calculator in Desmos, type \( \mathrm{sin(} 50 \mathrm{)} \) and hit \( \mathrm{ENTER} \) (since the scientific calculator in Desmos defaults to degree mode, it will interpret the \( 50 \) as \( 50^{ \circ } \)). Desmos returns \(0.7660444431\) (please verify).

It is important to note that the values returned by the technology used in Example \( \PageIndex{ 1 } \) are not exact values; it turns out that the sine of \(50^{\circ}\) is an irrational number, and your calculator shows as many digits as its display will allow (not all sine values are as "nice" as the sine of \(30^{\circ}\)). Unless otherwise instructed, we round to four decimal places, so we write\[\sin \left(50^{\circ}\right) \approx 0.7660.\nonumber\]Take note of using the approximation sign, \( \approx \), instead of the equal sign - this is important!

Checkpoint \( \PageIndex{ 1 } \)

1. Use a calculator to complete the table, rounding answers to four decimal places.

   \(\theta\)	\(0^{\circ}\)	\(10^{\circ}\)	\(20^{\circ}\)	\(30^{\circ}\)	\(40^{\circ}\)	\(50^{\circ}\)	\(60^{\circ}\)	\(70^{\circ}\)	\(80^{\circ}\)	\(89^{\circ}\)
   \(\tan\left( \theta\right)\)

2. What do you notice about the values of \(\tan\left( \theta\right)\) as \(\theta\) increases from \(0^{\circ}\) to \(89^{\circ}\)? If the values of \(\tan \left(\theta\right)\) are plotted against the values of \(\theta\), will the graph be a straight line? Why or why not?

Answers

1. \(\theta\)	\(0^{\circ}\)	\(10^{\circ}\)	\(20^{\circ}\)	\(30^{\circ}\)	\(40^{\circ}\)	\(50^{\circ}\)	\(60^{\circ}\)	\(70^{\circ}\)	\(80^{\circ}\)	\(90^{\circ}\)
   \(\tan \left(\theta\right)\)	0	0.1763	0.3640	0.5774	0.8391	1.1918	1.7321	2.7475	5.6713	57.2900

2. The values of \(\tan\left( \theta\right)\) increase seemingly without bound as \(\theta\) increases from \(0^{\circ}\) to \(89^{\circ}\). The graph will not be a line because the slopes between successive points are not constant.

Example \(\PageIndex{2}\)

Use technology to compute the value of each trigonometric function.

1. \( \cos\left( 23.7^{ \circ } \right) \)
2. \( \tan\left( 72.13^{ \circ } \right) \)
3. \( \sin^2\left( 10^{ \circ } \right) \)

Solutions

1. \( \cos\left( 23.7^{ \circ } \right) \approx 0.9156625933 \approx 0.9157 \)
2. \( \tan\left( 72.13^{ \circ } \right) \approx 3.101611189 \approx 3.1016 \)
3. To compute \( \sin^2\left( 10^{ \circ } \right) \), we need to recall that\[ \sin^2\left( 10^{ \circ } \right) = \left[ \sin\left( 10^{ \circ } \right) \right]^2. \nonumber \]Therefore, we start by getting the approximation \( \sin\left( 10^{ \circ } \right) \approx 0.1736481777 \). Using as many of these digits as possible, we then square the result to get\[ \sin^2\left( 10^{ \circ } \right) \approx \left( 0.1736481777 \right)^2 \approx 0.03015368961 \approx 0.0304. \nonumber \]

Caution: Save Rounding for the Final Answer

Example \( \PageIndex{ 2c } \) demonstrates a significant point that bears repeating - rounding is for display purposes only! Never round a result and then use that rounded result for other computations.

For example, had we rounded our approximation of \( \sin\left( 10^{ \circ } \right) \) to be 0.1736 and then squared, we would have incorrectly stated \( \sin^2\left( 10^{ \circ } \right) \approx 0.0301 \). While the difference between this result and the more accurate result of \( 0.0304 \) may seem insignificant, these rounding errors can propagate in such a way as to make massive differences between answers.

Checkpoint \( \PageIndex{ 2 } \)

1. Use a calculator to complete the table. Round the values of sine and cosine to four decimal places.

   \(\theta\)	\(0^{\circ}\)	\(10^{\circ}\)	\(20^{\circ}\)	\(30^{\circ}\)	\(40^{\circ}\)	\(50^{\circ}\)	\(60^{\circ}\)	\(70^{\circ}\)	\(80^{\circ}\)	\(90^{\circ}\)
   \(\sin\left( \theta\right)\)
   \(\cos\left( \theta\right)\)

2. Is there a pattern to the values of sine and cosine? Why this is true? (Hint: If one (non-right) angle of a right triangle measures \(x\) degrees, how big is the other angle? Sketch the triangle and label each angle's opposite and adjacent sides.)

Answers

1. \(\theta\)	\(0^{\circ}\)	\(10^{\circ}\)	\(20^{\circ}\)	\(30^{\circ}\)	\(40^{\circ}\)	\(50^{\circ}\)	\(60^{\circ}\)	\(70^{\circ}\)	\(80^{\circ}\)	\(90^{\circ}\)
   \(\sin \left(\theta\right)\)	0	0.1737	0.3420	0.5	0.6428	0.7660	0.8660	0.9397	0.9848	1
   \(\cos \left(\theta\right)\)	1	0.9849	0.9397	0.8660	0.7660	0.6428	0.5	0.3420	0.1737	0

2. The cosine of \(\theta\) is equal to the sine of the complement of \(\theta\), or \(\cos \left(\theta\right) = \sin(90 − \theta)\). This result confirms the Cofunction Identity from the previous section.

Now that we have access to technology to approximate the value of trigonometric functions at non-special angles, we can revisit simplifying and evaluating trigonometric expressions.

Example \( \PageIndex{ 3} \)

Simplify, and evaluate for \(z=40^{\circ}\).\[3 \sin \left(z\right)-\sin \left(z\right) \tan \left(z\right)+3 \sin \left(z\right)\nonumber \]

Solution

We can combine like terms to get\[6 \sin \left(z\right)-\sin \left(z\right) \tan \left(z\right)\nonumber \]Because \(40^{\circ}\) is not one of the angles for which we know exact trig values, we use a calculator to evaluate the expression. It is very important to make sure we save any rounding until the very end of the computation. Therefore, we enter the following keystrokes into our calculator (or other technology):\[ 6 \quad \times \quad \mathrm{SIN} \quad 40 \quad \mathrm{)} \quad \mathrm{-} \quad \mathrm{SIN} \quad 40 \quad \mathrm{)} \quad \times \quad \mathrm{TAN} \quad 40 \quad \mathrm{ENTER} \nonumber \]Doing so, we get approximately 3.3174.

Checkpoint \( \PageIndex{ 3 } \)

Simplify, and evaluate for \(x=25^{\circ}, y=70^{\circ}\).\[3 \cos \left(x\right)+\cos \left(y\right)-2 \cos \left(y\right)+\cos \left(x\right)\nonumber \]

Answer

\(3.2832\)

Unlike the fundamental trigonometric functions, calculators do not have keys for the cosecant, secant, and cotangent functions. Instead, we calculate their values as reciprocals.

Example \( \PageIndex{ 4 } \)

Use technology to approximate \(\sec \left(47^{\circ}\right)\) to three decimal places.

Solution

Enter\[1 \div \cos 47 ) \text { ENTER } \nonumber \]to obtain \(\sec \left(47^{\circ}\right) \approx 1.466\). Or we can calculate \(\cos \left(47^{\circ}\right)\) first, and then use the reciprocal key:\[\cos 47 ) \text{ ENTER } x^{-1} \text{ ENTER } \nonumber \]

Checkpoint \( \PageIndex{ 4 } \)

Use technology to approximate \(\csc \left(82^{\circ}\right)\) to three decimal places.

Answer

1.010

Small Angles: Degrees, Minutes, and Seconds

The traditional angular measurement system we have covered is called the Decimal Degree (DD) system. Decimal Degrees offer simplicity and ease of use, making them a preferred choice for everyday applications like GPS navigation. However, it’s essential to recognize that they are not a one-size-fits-all solution. In scenarios where precision is paramount, such as offshore navigation or land surveying, a slightly modified Degree-Minute-Second (DMS) system shines.

The DMS system divides degrees into smaller units called minutes and seconds. One minute is \(\frac{1}{60}\) of a degree, and 1 second is \(\frac{1}{60}\) of a minute, or \(\frac{1}{3600}\) of a degree. We use the following notation for minutes and seconds.

Definition: Minutes and Seconds

• One minute: \(\quad 1^{\prime}=\dfrac{1^{\circ}}{60}\)
• One second: \(\quad 1^{\prime \prime}=\dfrac{1^{\prime}}{60}=\dfrac{1^{\circ}}{3600}\)

To convert a measure of \(42.125^{\circ}\) to the DMS system, we start by noting that \(42.125^{\circ} = 42^{\circ} + 0.125^{\circ}\). Converting the partial amount of degrees to minutes, we find \(0.125^{\circ} \left( \frac{60^{\prime}}{1^{\circ}} \right) = 7.5^{\prime} = 7^{\prime} + 0.5^{\prime}\). Converting the partial amount of minutes to seconds gives \(0.5^{\prime} \left(\frac{60^{\prime\prime}}{1^{\prime}} \right) = 30^{\prime\prime}\). Putting it all together yields\[\begin{array}{rcl}
42.125^{\circ} & = & 42^{\circ} + 0.125^{\circ} \\
& = & 42^{\circ} + 7.5^{\prime} \\
& = & 42^{\circ} + 7^{\prime} + 0.5^{\prime} \\
& = & 42^{\circ} + 7^{\prime} + 30^{\prime\prime} \\
& = & 42^{\circ}\, 7^{\prime}\, 30^{\prime\prime} \\
\end{array}\nonumber\]

On the other hand, to convert \(117^{\circ}\,15^{\prime}\,45^{\prime\prime}\) to decimal degrees, we first compute \(15^{\prime} \left(\frac{1^{\circ}}{60^{\prime}}\right) = \frac{1}{4}^{\circ}\) and \(45^{\prime\prime} \left(\frac{1^{\circ}}{3600^{\prime\prime}}\right) = \frac{1}{80}^{\circ}\). Then we find\[\begin{array}{rcl}
117^{\circ}\,15^{\prime}\,45^{\prime\prime} & = & 117^{\circ} + 15^{\prime} + 45^{\prime\prime} \\
& = & 117^{\circ} + \frac{1}{4}^{\circ} + \frac{1}{80}^{\circ} \\
& = & \frac{9381}{80}^{\circ} \\
& = & 117.2625^{\circ} \\
\end{array}\nonumber\]

Example \( \PageIndex{5} \)

Let \(\alpha = 111.371^{\circ}\) and \(\beta = 37^{\circ} \, 28^{\prime} \, 17^{\prime\prime}\).

1. Convert \(\alpha\) to the DMS system. Round your answer to the nearest second.
2. Convert \(\beta\) to Decimal Degrees. Round your answer to the nearest thousandth of a degree.
3. Sketch \(\alpha\) and \(\beta\).
4. Find a supplementary angle for \(\alpha\).
5. Find a complementary angle for \(\beta\).

Solutions

1. To convert \(\alpha\) to the DMS system, we start with \(111.371^{\circ} = 111^{\circ} + 0.371^{\circ}\). Next we convert \(0.371^{\circ} \left(\frac{60^{\prime}}{1^{\circ}}\right) = 22.26^{\prime}\). Writing \(22.26^{\prime} = 22^{\prime}+ 0.26^{\prime}\), we convert \(0.26^{\prime} \left( \frac{60^{\prime\prime}}{1^{\prime}} \right) = 15.6^{\prime\prime}\). Hence,\[\begin{array}{rcl}
   111.371^{\circ} & = & 111^{\circ} + 0.371^{\circ} \\
   & = & 111^{\circ} + 22.26^{\prime} \\
   & = & 111^{\circ} + 22^{\prime} + 0.26^{\prime} \\
   & = & 111^{\circ} + 22^{\prime} + 15.6^{\prime\prime} \\
   & = & 111^{\circ}\,22^{\prime}\,15.6^{\prime\prime} \\
   \end{array}\nonumber\]Rounding to seconds, we obtain \(\alpha \approx 111^{\circ} \, 22^{\prime} \, 16^{\prime\prime}\).
2. To convert \(\beta\) to decimal degrees, we convert \(28^{\prime} \left(\frac{1^{\circ}}{60^{\prime}}\right) = \frac{7}{15}^{\circ}\) and \(17^{\prime\prime}\left(\frac{1^{\circ}}{3600^{\prime}}\right) = \frac{17}{3600}^{\circ}\). Putting it all together, we have\[\begin{array}{rcl}
   37^{\circ}\,28^{\prime}\,17^{\prime\prime} & = & 37^{\circ} + 28^{\prime} + 17^{\prime\prime} \\
   & = & 37^{\circ} + \dfrac{7}{15}^{\circ} + \dfrac{17}{3600}^{\circ} \\
   & = & \dfrac{134897}{3600}^{\circ} \\
   & \approx & 37.471^{\circ} \\
   \end{array}\nonumber\]
3. To sketch \(\alpha\), we first note that \(90^{\circ} < \alpha < 180^{\circ}\). If we divide this range in half, we get \(90^{\circ} < \alpha < 135^{\circ}\), and once more, we have \(90^{\circ} < \alpha < 112.5^{\circ}\). This gives us a pretty good estimate for \(\alpha\), as shown below. Proceeding similarly for \(\beta\), we find \(0^{\circ} < \beta < 90^{\circ}\), then \(0^{\circ} < \beta < 45^{\circ}\), \(22.5^{\circ} < \beta < 45^{\circ}\), and lastly, \(33.75^{\circ} < \beta < 45^{\circ}\).

   

4. To find a supplementary angle for \(\alpha\), we seek an angle \(\theta\) so that \(\alpha + \theta = 180^{\circ}\). We get \(\theta = 180^{\circ} - \alpha = 180^{\circ} - 111.371^{\circ} = 68.629^{\circ}\).
5. To find a complementary angle for \(\beta\), we seek an angle \(\gamma\) so that \(\beta + \gamma = 90^{\circ}\). We get \(\gamma = 90^{\circ} - \beta = 90^{\circ} - 37^{\circ}\,28^{\prime}\,17^{\prime\prime}\). While we could reach for the calculator to obtain an approximate answer, let's do something more mathematically engaging. We first rewrite \(90^{\circ} = 90^{\circ} \, 0^{\prime} \, 0^{\prime\prime} = 89^{\circ} \, 60^{\prime} \, 0^{\prime\prime} = 89^{\circ}\,59^{\prime}\,60^{\prime\prime}\). In essence, we are "borrowing" \(1^{\circ} = 60^{\prime}\) from the degree place, and then "borrowing" \(1^{\prime} = 60^{\prime\prime}\) from the minutes place. This yields, \(\gamma = 90^{\circ} - 37^{\circ}\,28^{\prime}\,17^{\prime\prime} = 89^{\circ}\,59^{\prime} \, 60^{\prime\prime} - 37^{\circ} \, 28^{\prime} \, 17^{\prime\prime} = 52^{\circ} \, 31^{\prime} \, 43^{\prime\prime}\).

Checkpoint \(\PageIndex{5}\)

1. Convert \( 10^{ \circ }\, 45^{\prime} \) to DD.
2. Convert \( 27.25^{ \circ } \) to DMS.

Answers

1. \( 10.75^{ \circ } \)
2. \( 27^{ \circ }\,15^{\prime} \)

Calculator Note

Most scientific and graphing calculators have keys to enter angles in DMS format. You may also have keys or commands that let you convert from one format to another. Consult your calculator’s manual to see how this is done with your particular model.

Some argue that DMS coordinates belong to a bygone era, overshadowed by the convenience of Decimal Degrees and digital mapping tools. However, this couldn’t be further from the truth. DMS coordinates remain a cornerstone in various industries, including maritime, aviation, surveying, and astronomy, where precision and tradition go hand in hand. These coordinates have stood the test of time, adapting to modern technology while retaining their significance.

Another misconception is that DMS coordinates have limited utility, primarily confined to specialized fields. While DMS coordinates are prevalent in aviation, maritime, and surveying, they also have broader applications in geocaching, emergency services, and outdoor recreational activities. Their precision and familiarity make them a versatile choice in various contexts.

Sometimes, you need to add or subtract angles in the DMS system.

Example \(\PageIndex{6}\)

Perform the arithmetic.

1. \( 23^{ \circ }\, 16^{\prime}\, 47^{\prime\prime} + 17^{ \circ }\, 50^{\prime}\, 24^{\prime\prime} \)
2. \( 23^{ \circ }\, 16^{\prime}\, 47^{\prime\prime} - 17^{ \circ }\, 50^{\prime}\, 24^{\prime\prime} \)

Solutions

1. When adding angles in the DMS system, it is best to perform the arithmetic as we did in elementary school. This is because we will be "carrying" between measures (i.e., carrying \( 60^{\prime\prime} \) to \( 1^{\prime} \), and \( 60^{\prime} \) to \( 1^{ \circ } \)).\[ \begin{array}{rclcr}
   \begin{array}{cccc}
   & 23^{ \circ } & 16^{\prime} & 47^{\prime\prime} \\
   + & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & & & 71^{\prime\prime} \\
   \end{array} & \implies & \begin{array}{cccc}
   & & 1^{\prime} & \\
   & 23^{ \circ } & 16^{\prime} & 47^{\prime\prime} \\
   + & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & & & 11^{\prime\prime} \\
   \end{array} & \quad & (\text{Carrying the }60^{\prime\prime} \text{ to }1^{\prime}) \\
   & \implies & \begin{array}{cccc}
   & & 1^{\prime} & \\
   & 23^{ \circ } & 16^{\prime} & 47^{\prime\prime} \\
   + & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & & 67^{\prime} & 11^{\prime\prime} \\
   \end{array} & \quad & \\
   & \implies & \begin{array}{cccc}
   & 1^{ \circ } & 1^{\prime} & \\
   & 23^{ \circ } & 16^{\prime} & 47^{\prime\prime} \\
   + & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & & 7^{\prime} & 11^{\prime\prime} \\
   \end{array} & \quad & (\text{Carrying the }60^{\prime} \text{ to }1^{\circ}) \\
   & \implies & \begin{array}{cccc}
   & 1^{ \circ } & 1^{\prime} & \\
   & 23^{ \circ } & 16^{\prime} & 47^{\prime\prime} \\
   + & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & 41^{ \circ } & 7^{\prime} & 11^{\prime\prime} \\
   \end{array} & \quad & \\
   \end{array} \nonumber \]Therefore, the sum is \( 41^{ \circ } \, 7^{\prime} \, 11^{\prime\prime} \).
2. When subtracting angles in the DMS system, it is best to perform the arithmetic like we did in elementary school. This is because we will be "borrowing" between measures (i.e., borrowing \( 1^{\prime} \) to \( 60^{\prime\prime} \), and \( 1^{\circ} \) to \( 60^{ \prime } \)).\[ \begin{array}{rclcr}
   \begin{array}{cccc}
   & 23^{ \circ } & 16^{\prime} & 47^{\prime\prime} \\
   - & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & & & 23^{\prime\prime} \\
   \end{array} & \implies & \begin{array}{cccc}
   & 22^{ \circ } & 76^{\prime} & 47^{\prime\prime} \\
   - & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & & & 23^{\prime\prime} \\
   \end{array} & \quad & (\text{Borrowing the }1^{\circ} \text{ to }60^{\prime}) \\
   & \implies & \begin{array}{cccc}
   & 22^{ \circ } & 76^{\prime} & 47^{\prime\prime} \\
   - & 17^{ \circ } & 50^{\prime} & 24^{\prime\prime} \\
   \hline & 5^{ \circ } & 26^{\prime} & 23^{\prime\prime} \\
   \end{array} & \quad & \\
   \end{array} \nonumber \]Therefore, the difference is \( 5^{ \circ } \, 26^{\prime} \, 23^{\prime\prime} \).

Checkpoint \(\PageIndex{6}\)

1. Add \( 53^{ \circ } \, 34^{\prime} \, 12^{\prime\prime} \) and \( 10^{ \circ } \, 25^{\prime} \, 55^{\prime\prime} \).
2. Subtract \( 23^{ \circ } \, 12^{\prime} \) from \( 77^{ \circ } \).

Answers

1. \( 64^{ \circ } \, 0^{\prime} \, 7^{\prime\prime} \)
2. \( 53^{ \circ }\,48^{\prime} \)

Computing the value of a trigonometric function where the angle has been given in the DMS system is as simple as first converting the angle to the DD system.

Example \(\PageIndex{7}\)

Evaluate \( \cot\left( 10^{ \circ }\, 45^{\prime} \right) \).

Solution

In Checkpoint \( \PageIndex{ 5} \), you found \( 10^{ \circ }\, 45^{\prime} = 10.75^{ \circ } \). Thus,\[ \cot\left( 10^{ \circ }\, 45^{\prime} \right) = \cot\left( 10.75^{ \circ } \right) = \dfrac{1}{\tan\left( 10.75^{ \circ } \right)} \approx 5.2672. \nonumber \]

Checkpoint \(\PageIndex{7}\)

Evaluate \( \sec\left( 23^{ \circ }\, 16^{\prime}\, 47^{\prime\prime} \right) \).

Answer

\( \approx 1.0886 \)

Finding an Acute Angle Using a Calculator

While watching her niece at the playground, Nhat wonders how steep the slide is. She takes out her measuring tape and finds the slide to be 77 inches high over a horizontal distance of 136 inches, as shown below.

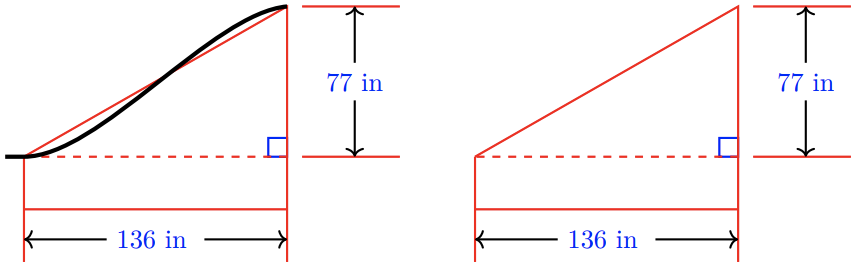
Nhat knows that one way to describe the steepness of an incline is to calculate its slope, which, in this case, is\[\dfrac{\Delta y}{\Delta x} = \dfrac{77}{136} \approx 0.5662.\nonumber \]However, she wants to know what angle the slide makes with the horizontal. Thinking about it for a moment, she realizes that the slope she had just calculated is also the tangent of the angle she wants (can you see this from the figures above?). This begs the question: If we know the tangent of an angle, can we find the angle? The answer is yes!

Locate the key labeled \(\mathrm{TAN}^{−1}\) on your calculator; it is probably the second function above the \(\mathrm{TAN}\) key. Enter\[ \mathrm{2nd} \quad \mathrm{TAN} \quad 0.5662 \nonumber \]to find that\[\tan ^{-1} \left( 0.5662 \right) \approx 29.5185^{\circ}.\nonumber \]This means that \(29.5185^{\circ}\) is the approximate angle whose tangent is \(0.5662\). We read the notation, \( \tan^{-1}\left( 0.5662 \right) \approx 29.5185^{\circ} \) as "inverse tangent of \(0.5662\) is approximately \(29.5185\) degrees."

Note: Use Degree Mode

Until later in this course, you should make sure your calculator is set to "degree" mode. If you do not do this, your answers, while correct in a different angular measure system, will be incorrect.

Caution: Do Not Use Rounded Values for Calculations

Before describing the inverse tangent, we must note the flaw in our work. We approximated the value of the fraction, \( \frac{77}{136} \), and then used that approximation to approximate the angle - this is very bad form. In truth, we should not have approximated \( \frac{77}{136} \), but instead just computed\[ \tan^{-1}\left( \dfrac{77}{136} \right) \approx 29.5175^{ \circ }. \nonumber \]Do you see that the returned angle from the inverse tangent is slightly different from our calculations using the rounded approximation of the fraction?

The moral of the story is that, whenever possible, do not use rounded or approximate values to get yet another approximation - this leads to a propagation of rounding errors.

When we find \(\tan ^{-1}\) of a number, we find an angle whose tangent is that number. Similarly, \(\sin ^{-1}\) and \(\cos ^{-1}\) are read as "inverse sine" and "inverse cosine." They find an angle with the given sine or cosine.

Example \( \PageIndex{ 8} \)

Find the angle whose sine is \(0.6834\).

Solution

Enter \[ \mathrm{2nd} \quad \mathrm{SIN} \quad 0.6834\nonumber \]into your calculator to find\[\sin ^{-1} \left(0.6834\right) \approx 43.11^{\circ}. \nonumber \]So \(43.11^{\circ}\) is the angle whose sine is approximately \(0.6834\). Alternatively, we can say that\[\sin \left(43.11^{\circ}\right) \approx 0.6834. \nonumber \]You can check the last equation on your calculator.

Note: Equivalent Statements

In Example \( \PageIndex{ 8} \), the two equations\[\sin \left(43.11^{\circ} \right) \approx 0.6834 \quad \text { and } \quad \sin ^{-1}\left( 0.6834\right) \approx 43.11^{\circ}\nonumber \]say the same thing in different ways.

Caution: Inverse Trigonometric Functions are NOT Reciprocals

The notation \(\sin ^{-1} \left(x\right)\) does not mean \(\frac{1}{\sin\left( x\right)}\)!

We indeed use negative exponents to indicate reciprocals of numbers, for example, \(a^{-1}=\frac{1}{a}\) and \(3^{-1}=\frac{1}{3}\). However, "sin" by itself is not a variable.

• \(\sin ^{-1} \left(x\right)\) means "the angle whose sine is \(x\)"
• \(\frac{1}{\sin \left(x\right)}\) means "the reciprocal of the sine of angle \(x\)"

(You may recall that \(f^{-1}(x)\) denotes the inverse function for \(f(x)\). We will study trigonometric functions in Chapter 4.)

Checkpoint \( \PageIndex{ 8} \)

Write the following fact in two different ways: \(68^{\circ}\) is the angle whose cosine is \(0.3746\).

Answer

\(\cos \left(68^{\circ}\right)=0.3746\) or \(\cos ^{-1}\left(0.3746\right)=68^{\circ}\)

Note: Inputs and Outputs of Inverse Trigonometric Functions

Without going into too much detail (yet), it is essential to note that an inverse trigonometric function's input (a.k.a., the argument) is a ratio. The output is an angle.

Example \(\PageIndex{9}\)

Find the acute angle for which the equation is true. Round answers to the nearest tenth.

1. \( \cos\left( \beta \right) = 0.28 \)
2. \( \tan\left( \kappa \right) = 1.93 \)

Solutions

1. We use the following button sequence:\[ \mathrm{2nd} \quad \mathrm{COS} \quad 0.28 \quad \mathrm{ENTER}. \nonumber \]This returns \( 73.73979529 \). Hence, \( \beta \approx 73.7^{ \circ } \).
2. Using the sequence\[ \mathrm{2nd} \quad \mathrm{TAN} \quad 1.93 \quad \mathrm{ENTER}, \nonumber \]we get \( 62.60975803 \). Hence, \( \kappa \approx 62.6^{ \circ } \).

Checkpoint \(\PageIndex{9}\)

Find the acute angle for which \( \tan\left( \theta \right) = 1.23 \). Round your answer to the nearest tenth.

Answer

\( \theta \approx 50.9^{ \circ } \)

Finding acute angles is slightly more complex when the equation involves the cosecant, secant, or cotangent. A good rule of thumb is to rewrite the equation in terms of the fundamental trigonometric functions using the Reciprocal Identities.

Example \(\PageIndex{10}\)

Suppose \( x \) is an acute angle within a right triangle. Solve each equation. Round answers to two decimal places.

1. \( \sec\left( x \right) = 8.104 \)
2. \( 3 \cot\left( x \right) - 2 = 7 \)

Solutions

1. We first rewrite the equation as\[\dfrac{1}{\cos\left( x \right)} = 8.104 \implies \cos\left( x \right) = \dfrac{1}{8.104} \nonumber \]We then enter\[ \mathrm{2nd} \quad \mathrm{COS} \quad 1 \quad \div \quad 8.104\nonumber \]into the calculator to find\[\cos ^{-1} \left( \frac{1}{8.104}\right) \approx 82.91^{\circ}. \nonumber \]Therefore, the solution to \( \sec\left( x \right) = 8.104 \) is \( x \approx 82.91^{\circ} \).
2. The equation handed to us needs to be simplified into the form \( \cot\left( \text{angle} \right) = \text{number} \) before we can find the angle.\[\begin{array}{rrcl}
   & 3 \cot\left( x \right) - 2 & = & 7 \\
   \implies & 3 \cot \left( x \right) & = & 9 \\
   \implies & \cot \left( x \right) & = & 3 \\
   \end{array} \nonumber \]We now rewrite the cotangent as the tangent using the Reciprocal Identities.\[ \cot\left( x \right) = 3 \implies \dfrac{1}{\tan\left( x \right)} = 3 \implies \tan\left( x \right) = \dfrac{1}{3} \nonumber \]Finally, we grab our technology and enter\[ \mathrm{2nd} \quad \mathrm{TAN} \quad 1 \quad \div \quad 3\nonumber \]into the calculator to find\[\tan ^{-1} \left(\frac{1}{3}\right) \approx 18.43^{\circ} \nonumber \]Therefore, the solution to \( 3 \cot\left( x \right) - 2 = 7 \) is \( x \approx 18.43^{\circ} \).

Checkpoint \(\PageIndex{10}\)

Let \( \omega \) be an acute angle within a right triangle. Solve \( 2 \csc\left( \omega \right) + 3 = 11 \). Round the answer to two decimal places.

Answer

\(\omega \approx 14.48^{\circ}\)

Activity: Trigonometric Ratios

1. Using Ratios and Proportions
   Two related quantities or variables are proportional if their ratio is always the same.
   1. 1. On any given day, the cost of filling up your car’s gas tank is proportional to the number of gallons of gas you buy. For each purchase below, compute the ratio\[\dfrac{\text { total cost of gasoline }}{\text { number of gallons }} \nonumber\]

         Gallons of Gas Purchased	Total Cost	\(\dfrac{\text { Dollars }}{\text { Gallon }}\)
         5	$14.45
         12	$34.68
         18	$52.02

      2. Write an equation that you can solve to answer the question: How much does 21 gallons of gas cost? Use the ratio \(\frac{\text { Dollars }}{\text { Gallon }}\) in your equation.
      3. Write an equation that you can solve to answer the question: How many gallons of gas can you buy for \(\$ 46.24\)? Use the ratio \(\frac{\text { Dollars }}{\text { Gallon }}\) in your equation.
   2. A recipe for coffee cake calls for \(\frac{3}{4}\) cup of sugar and \(1 \frac{3}{4}\) cup of flour.
      1. What is the ratio of sugar to flour? Write your answer as a common fraction, then give a decimal approximation rounded to four places.
         
         
         For parts (b) and (c) below, write an equation that you can solve to answer the question. Use the ratio \(\frac{\text { Amount of sugar }}{\text { Amount of flour }}\) your equation.
      2. How much sugar should you use if you use 4 cups of flour? Compute your answer in two ways: write the ratio as a common fraction and then write the ratio as a decimal approximation. Are your answers the same?
      3. How much flour should you use if you use 4 cups of sugar? Compute your answer in two ways: write the ratio as a common fraction and then write the ratio as a decimal approximation. Are your answers the same?
   3. You are making a scale model of the Eiffel Tower, which is 324 meters tall and 125 meters wide at its base.

      

      1. Compute the ratio of the base width to the tower's height. Round your answer to four decimal places.
         
         Use your ratio to write equations and answer the questions below:
      2. If the base of your model is 8 inches wide, how tall should the model be?
      3. If you make a larger model that is 5 feet tall, how wide will the base be?
2. Similar Triangles
   1. Recall that two triangles are similar if their corresponding sides are proportional. The corresponding angles of similar triangles are equal.
      1. What is the ratio of the two given sides in each triangle? Are the corresponding sides of the three triangles proportional? How do we know that \(\alpha = \beta = \gamma\)?

         

      2. Find the hypotenuse of each right triangle.
      3. Use the sides of the appropriate triangle to compute \(\sin \alpha, \sin \beta\), and \(\sin \gamma\). Round your answers to four decimal places. Does the sine of an angle depend on the lengths of its sides?
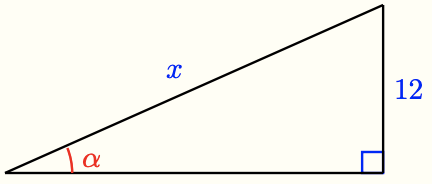
      4. How do you know that the triangle below is similar to the three triangles in part (a)? Write an equation using the ratio from part (c) to find \(x\).

         

   2. In the three right triangles below, the angle \(\theta\) is the same size.

      

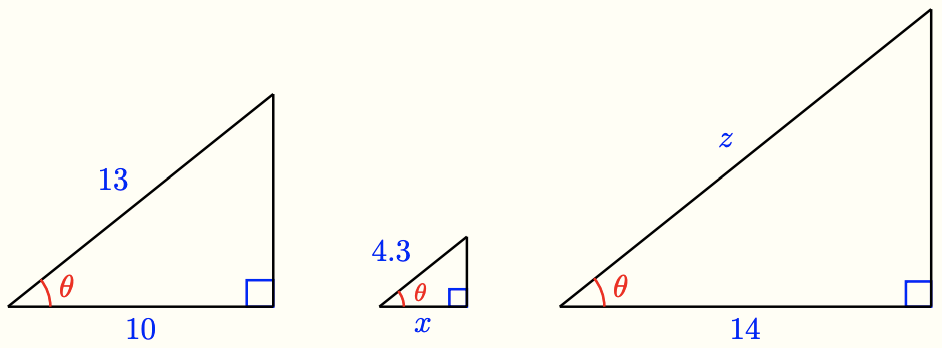
      1. Use the first triangle to calculate \(\cos \theta\). Round your answer to four decimal places.
      2. In the second triangle, explain why \(\frac{x}{4.3} = \frac{10}{13}\). Write an equation using your answer to part (a) and solve it to find \(x\).
      3. Write and solve an equation to find \(z\) in the third triangle.
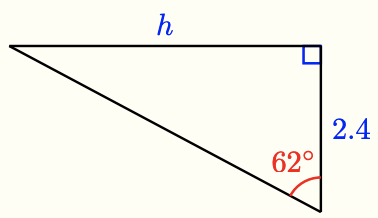
   3. 1. Use your calculator to find the value of \(\frac{h}{2.4}\). (Hint: Which trigonometric ratio should you use?) What is the length of side \(h\)?

         

      2. What is the value of \(\frac{6}{w}\) for the triangle below? Write an equation and solve for \(w\).

         

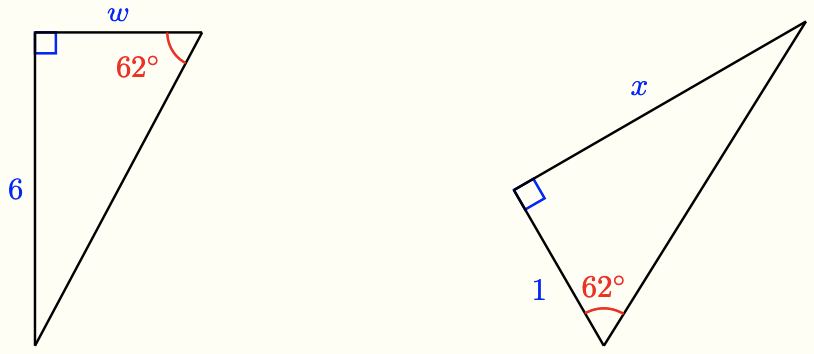
      3. Write an equation and solve it to find \(x\) in the triangle above.

Activity: Obtuse Angles

An obtuse angle has measure between \(90^{\circ}\) and \(180^{\circ}\), exclusively. In this activity, we will investigate the trigonometric functions of an obtuse angle.

1. Draw an angle \(\theta\) in standard position with the point \(P(6,4)\) on its terminal side.
2. Find \(r\), the distance from the origin to \(P\).
3. Calculate all six trigonometric functions of \(\theta\). Give both exact answers and decimal approximations rounded to four places.
4. Use the inverse cosine key on your calculator to find \(\theta\). Use your calculator to verify the values of \(\sin \left(\theta\right), \cos \left(\theta\right)\), and \(\tan \left(\theta\right)\) that you found in part (c).
5. Draw another angle \(\phi\) in standard position with the point \(Q(-6,4)\) on its terminal side. Explain why \(\phi\) is the supplement of \(\theta\). (Hint: Consider the right triangles formed by drawing vertical lines from \(P\) and \(Q\)).
6. Can you use the right triangle definition of the trigonometric functions to compute the sine and cosine of \(\phi\)? Why or why not?
7. Calculate all six trigonometric functions of \( \phi \). How are these trigonometric values of \(\phi\) related to the trigonometric values of \(\theta\)?
8. Explain why \(\theta\) and \(\phi\) have the same sine but different cosines.
9. Use the inverse cosine key on your calculator to find \(\phi\). Use your calculator to verify the values of \(\sin \left(\phi\right), \cos \left(\phi\right)\), and \(\tan \left(\phi\right)\) that you found in part (g).
10. Compute \(180^{\circ}-\phi\). What answer should you expect to get?

---

Skills Refresher

Review the following skills you will need for this section.

Skills Refresher

For Problems 1 - 4, write two more ratios equivalent to the given fraction.

1. \(\dfrac{10}{4}\)

2. \(\dfrac{6}{8}\)

3. \(0.6\)

4. \(1.5\)

For Problems 5 - 8, compute the slope of the line.

5.  

   

6.  

   

7.  

   

8.  

   

For Problems 9 - 10, solve.

9. \(\dfrac{12}{x} = 48\)

10. \(\dfrac{60}{x} = 80\)

Answers

(Many answers are possible for 1-4.)

1. \(\dfrac{5}{2}, \dfrac{20}{8}\)

2. \(\dfrac{3}{4}, \dfrac{12}{16}\)

3. \(\dfrac{3}{5}, \dfrac{12}{20}\)

4. \(\dfrac{6}{4}, \dfrac{12}{8}\)

5. \(\dfrac{2}{5}\)

6. \(\dfrac{-8}{5}\)

7. \(\dfrac{-6}{5}\)

8. \(\dfrac{1}{2}\)

9. \(\dfrac{1}{4}\)

10. \(\dfrac{3}{4}\)

---

Homework

Vocabulary Check

1. Calculators and other technology have two modes that deal with the values of trigonometric functions - ___ mode and ___ mode. At this point, we only use ___ mode.

Concept Check

2. Explain how you would convert an angle given in Decimal Degrees (DD) to Degrees-Minutes-Seconds (DMS).

3. Does your calculator give you the exact decimal values for the trigonometric ratios of acute angles?

4. \( 1^{ \circ } \) is equal to ___ minutes(s).

5. \( 1^{ \circ } \) is equal to ___ second(s).

6. \( 1^{\prime} \) is equal to ___ degree(s).

7. \( 1^{\prime} \) is equal to ___ seconds(s).

8. \( 1^{\prime\prime} \) is equal to ___ degree(s).

9. \( 1^{\prime\prime} \) is equal to ___ minutes(s).

10. The \( \mathrm{SIN} \), \( \mathrm{COS} \), and \( \mathrm{TAN} \) keys on a calculator (or other technology) returns\[ \text{the value of the trigonometric function} \qquad \text{an angle} \nonumber \](circle one) when you input\[ \text{the value of the trigonometric function} \qquad \text{an angle} \nonumber \](circle one).

11. The \( \mathrm{SIN}^{-1} \), \( \mathrm{COS}^{-1} \), and \( \mathrm{TAN}^{-1} \) keys on a calculator (or other technology) returns\[ \text{the value of the trigonometric function} \qquad \text{an angle} \nonumber \](circle one) when you input\[ \text{the value of the trigonometric function} \qquad \text{an angle} \nonumber \](circle one).

12. Min and Paige try to approximate \( 2.1 \tan\left( 37^{ \circ } \right) \). Min types the following into her calculator\[ 2.1 \quad \times \quad \mathrm{TAN} \quad 37 \quad \mathrm{ENTER}, \nonumber \]and the calculator returns approximately 1.5825; however, Paige types\[ \mathrm{TAN} \quad 37 \quad \times \quad 2.1 \quad \mathrm{ENTER} \nonumber \]into her calculator and gets an approximation of 4.5864. They each have their calculators set to Degree Mode, so that's not the issue. Who has the wrong approximation? If she cannot change the order of what she types into her calculator, but can add or remove a button press, what can she do to fix her error?

True or False? For Problems 13 - 14, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

13. \( \cot^{-1}\left( \theta \right) = \dfrac{1}{\cot\left( \theta \right)} = \tan\left( \theta \right)\).

14. \( \cos^{-1}\left( \theta \right) = \sin\left( \theta \right) \)

Basic Skills

For Problems 15 - 22, evaluate. Round answers to 3 decimal places.

15. \(\sin \left(53^{\circ}\right)\)

16. \(\cos \left(18^{\circ}\right)\)

17. \(\tan \left(5^{\circ}\right)\)

18. \(\sin \left(85^{\circ}\right)\)

19. \(\csc \left(27^{\circ}\right)\)

20. \(\sec \left(8^{\circ}\right)\)

21. \(\cot \left(65^{\circ}\right)\)

22. \(\csc \left(11^{\circ}\right)\)

23.  

    1. Fill in the table for values of \(\tan \theta\). Round your answers to four decimal places.

       \(\theta\)	\(0^{\circ}\)	\(10^{\circ}\)	\(20^{\circ}\)	\(30^{\circ}\)	\(40^{\circ}\)	\(50^{\circ}\)	\(60^{\circ}\)	\(70^{\circ}\)	\(80^{\circ}\)
       \(\tan \theta\)

    2. Fill in the table for values of \(\tan \theta\). Round your answers to three decimal places.

       \(\theta\)	\(81^{\circ}\)	\(82^{\circ}\)	\(83^{\circ}\)	\(84^{\circ}\)	\(85^{\circ}\)	\(86^{\circ}\)	\(87^{\circ}\)	\(88^{\circ}\)	\(89^{\circ}\)
       \(\tan \theta\)

    3. What happens to \(\tan \theta\) as \(\theta\) increases?

    4. What value does your calculator give for \(\tan 90^{\circ}\)? Why?

24.  

    1. Use your calculator to fill in a table of values for \(\cos \theta\), rounded to hundredths.

       \(\theta\)	\(0^{\circ}\)	\(15^{\circ}\)	\(30^{\circ}\)	\(45^{\circ}\)	\(60^{\circ}\)	\(75^{\circ}\)	\(90^{\circ}\)
       \(\cos \theta\)

    2. If you plotted the points in your table, would they lie on a straight line? Why or why not?

25.  

    1. Use your calculator to complete the table. Rounded your answers to hundredths

       \(\theta\)	\(14^{\circ}\)	\(22^{\circ}\)	\(35^{\circ}\)	\(42^{\circ}\)	\(58^{\circ}\)	\(78^{\circ}\)
       \(\tan \theta\)

    2. Use the values of \(\tan \theta\) to sketch all the angles listed in the table. Locate the vertex of each angle at the origin, and the initial side along the positive \(x\)-axis.

       

For Problems 26 - 31, evaluate the expressions using a calculator.

26.  

    1. \(\sin (10^{\circ} + 40^{\circ})\)

    2. \(\sin 10^{\circ} + \sin 40^{\circ}\)

    3. \(\sin 10^{\circ} \cos 40^{\circ} + \cos 10^{\circ} \sin 40^{\circ}\)

27.  

    1. \(\cos \left(20^{\circ}+50^{\circ}\right)\)

    2. \(\cos 20^{\circ}+\cos 50^{\circ}\)

    3. \(\cos 20^{\circ} \cos 50^{\circ}-\sin 20^{\circ} \sin 50^{\circ}\)

28.  

    1. \(\cos \left(2 \cdot 24^{\circ}\right)\)

    2. \(2 \cos 24^{\circ}\)

    3. \(2 \cos ^2\left(24^{\circ}\right)-1\)

29.  

    1. \(\cos \left(3 \cdot 19^{\circ}\right)\)

    2. \(3 \cos 19^{\circ}\)

    3. \(4 \cos ^3\left(19^{\circ}\right)-3 \cos 19^{\circ}\)

30.  

    1. \(\cos ^2\left(17^{\circ}\right)+\sin ^2\left(17^{\circ}\right)\)

    2. \(\sec ^2\left(86^{\circ}\right)-\tan ^2\left(86^{\circ}\right)\)

    3. \(\csc ^2\left(32.1^{\circ}\right)-\cot ^2\left(32.1^{\circ}\right)\)

31.  

    1. \(\sin ^2\left(25^{\circ}\right)+\cos^2\left(25^{\circ}\right)\)

    2. \(\dfrac{1}{\cos ^2\left(80^{\circ}\right)}-\tan^2\left(80^{\circ}\right)\)

    3. \(\dfrac{1}{\sin ^2\left(8^{\circ}\right)}-\cot^2\left(8^{\circ}\right)\)

For Problems 32 - 39, convert the angles into the DMS system. Round each of your answers to the nearest second.

32. \(18.9^{ \circ }\)

33. \(6.78^{ \circ }\)

34. \(55.17^{ \circ }\)

35. \(31.425^{ \circ }\)

36. \(70.214^{ \circ }\)

37. \(159.84^{ \circ }\)

38. \(220.43^{ \circ }\)

39. \(116.323^{ \circ }\)

For Problems 40 - 45, convert the angles into decimal degrees. Round each of your answers to three decimal places.

40. \(25^{\circ} \, 15^{\prime}\)

41. \(13^{\circ} \, 50^{\prime}\)

42. \(89^{\circ} \, 12^{\prime} \, 9^{\prime\prime}\)

43. \(32^{\circ} \, 10^{\prime} \, 12^{\prime\prime}\)

44. \(502^{\circ} \, 35^{\prime\prime}\)

45. \(237^{\circ} \, 58^{\prime} \, 43^{\prime\prime}\)

For Problems 46 - 48, find the complement of the given angle.

46. \(27^{\circ} \, 45^{\prime} \, 24^{\prime\prime}\)

47. \(88^{\circ} \, 10^{\prime} \, 36^{\prime\prime}\)

48. \(2^{\circ} \, 27^{\prime} \, 13^{\prime\prime}\)

For Problems 49 - 51, find the supplement of the given angle.

49. \(27^{\circ} \, 45^{\prime} \, 24^{\prime\prime}\)

50. \(88^{\circ} \, 10^{\prime} \, 36^{\prime\prime}\)

51. \(113^{\circ} \, 7^{\prime\prime}\)

For Problems 52 - 55, perform the arithmetic.

52. \(88^{\circ} \, 10^{\prime} \, 36^{\prime\prime} - 27^{\circ} \, 45^{\prime} \, 24^{\prime\prime}\)

53. \(88^{\circ} \, 10^{\prime} \, 36^{\prime\prime} + 27^{\circ} \, 45^{\prime} \, 24^{\prime\prime}\)

54. \(113^{\circ} \, 7^{\prime\prime} - 2^{\circ} \, 27^{\prime} \, 13^{\prime\prime}\)

55. \(113^{\circ} \, 7^{\prime\prime} + 2^{\circ} \, 27^{\prime} \, 13^{\prime\prime}\)

For Problems 56 - 63, evaluate the trigonometric function.

56. \( \sin\left( 27^{\circ} \, 45^{\prime} \, 24^{\prime\prime} \right) \)

57. \( \cos\left( 55^{\circ} \, 12^{\prime} \right) \)

58. \( \tan\left( 32^{\circ} \, 10^{\prime} \, 40^{\prime\prime} \right) \)

59. \( \csc\left( 7^{\circ} \, 7^{\prime} \, 50^{\prime\prime} \right) \)

60. \( \sec\left( 19^{\circ} \, 57^{\prime\prime} \right) \)

61. \( \cot\left( 27^{\circ} \, 55^{\prime} \right) \)

62. \( \sin\left( 5^{\circ} \, 55^{\prime} \right) \)

63. \( \tan\left( 89^{\circ} \, 40^{\prime} \, 1^{\prime\prime} \right) \)

For Problems 64 - 69, evaluate the expression.

64. \(\sin ^{-1} 0.2\)

65. \(\cos ^{-1} 0.8\)

66. \(\tan ^{-1} 1.5\)

67. \(\tan ^{-1} 2.5\)

68. \(\cos ^{-1} 0.2839\)

69. \(\sin ^{-1} 0.4127\)

70. Evaluate the expressions, and explain what each means.\[\sin ^{-1}(0.6), \quad\left(\sin 6^{\circ}\right)^{-1}\nonumber\]

71. Evaluate the expressions, and explain what each means.\[\cos ^{-1}(0.36), \quad\left(\cos 36^{\circ}\right)^{-1}\nonumber\]

Synthesis Questions

72. Here are two right triangles with a \(65^{\circ}\) angle.

    

    1. Measure the sides \(AB\) and \(BC\) with a ruler. Use the lengths to estimate \(\sin 65^{\circ}\).

    2. Measure the sides \(AD\) and \(DE\) with a ruler. Use the lengths to estimate \(\sin 65^{\circ}\).

    3. Use your calculator to look up \(\sin 65^{\circ}\). Compare your answers. How close were your estimates?

73. Use the figure in Problem 72 to calculate two estimates each for the cosine and tangent of \(65^{\circ}\). Compare your estimates to your calculator’s values for \(\cos 65^{\circ}\) and \(\tan 65^{\circ}\).

74. Here are two right triangles with a \(40^{\circ}\) angle.

    

    1. Measure the sides \(A B\) and \(A C\) with a ruler. Use the lengths to estimate \(\cos 40^{\circ}\).

    2. Measure the sides \(A D\) and \(A E\) with a ruler. Use the lengths to estimate \(\cos 40^{\circ}\).

    3. Use your calculator to look up \(\cos 40^{\circ}\). Compare your answers. How close were your estimates?

75. Use the figure in Problem 74 to calculate two estimates each for the cosine and tangent of \(40^{\circ}\). Compare your estimates to your calculator's values for \(\sin 40^{\circ}\) and \(\tan 40^{\circ}\).

For Problems 76 - 79, write two different equations for the statement.

76. The cosine of \(15^{\circ}\) is \(0.9659\).

77. The sine of \(70^{\circ}\) is \(0.9397\).

78. The angle whose tangent is \(3.1445\) is \(65^{\circ}\).

79. The angle whose cosine is \(0.0872\) is \(85^{\circ}\).

Applications

80. When a plane is tilted by an angle \(\theta\) from the horizontal, the time required for a ball starting from rest to roll a horizontal distance of \(l\) feet on the plane is\[t=\sqrt{\dfrac{l}{8} \csc (2 \theta)} \text { seconds } \nonumber \]

    

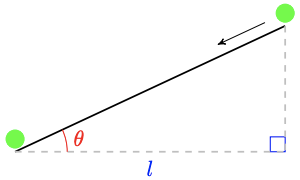
    1. How long, to the nearest 0.01 second, will it take the ball to roll 2 feet horizontally on a plane tilted by \(12^{\circ}\)?

    2. Solve the formula for \(l\) in terms of \(t\) and \(\theta\).

81. After a heavy rainfall, the depth, \(D\), of the runoff flow at a distance \(x\) feet from the watershed down a slope at angle \(\alpha\) is given by\[D=(k x)^{0.6}(\cot \left(\alpha\right))^{0.3} \text { inches } \nonumber \]where \(k\) is a constant determined by the surface roughness and the intensity of the runoff.

    1. How deep, to the nearest 0.01 inch, is the runoff 100 feet down a slope of \(10^{\circ}\) if \(k=0.0006\)?

    2. Solve the formula for \(x\) in terms of \(D\) and \(\alpha\).