24.2: Infinite Geometric Series

In some cases, it makes sense to add not only finitely many terms of a geometric sequence, but all infinitely many terms of the sequence! An informal and very intuitive infinite geometric series is exhibited in the next example.

Example $\PageIndex{1}$

Consider the geometric sequence $$1, \dfrac 1 2, \dfrac 1 4, \dfrac 1 8, \dfrac 1 {16}, \dots \nonumber$$

Solution

Here, the common ratio is $r=\dfrac 1 2$, and the first term is $a_1=1$, so that the formula for $a_n$ is $a_n=\left(\dfrac 1 2\right)^{n-1}$. We are interested in summing all infinitely many terms of this sequence:

$$1+ \dfrac 1 2+ \dfrac 1 4+ \dfrac 1 8+\dfrac 1 {16}+ \dots \nonumber$$

We add these terms one by one, and picture these sums on the number line:

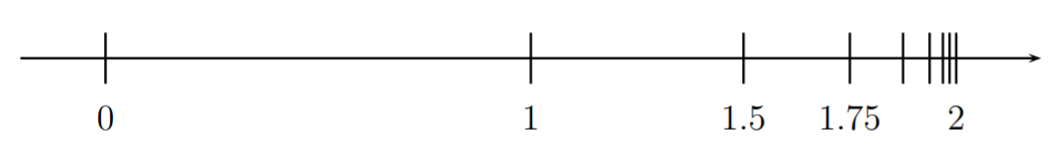
$$\begin{aligned} 1&= 1\\ 1+\dfrac 1 2&= 1.5\\ 1+\dfrac 1 2+\dfrac 1 4&= 1.75\\ 1+\dfrac 1 2+\dfrac 1 4+\dfrac 1 8 &= 1.875\\ 1+\dfrac 1 2+\dfrac 1 4+\dfrac 1 8+\dfrac 1 {16} &= 1.9375\end{aligned} \nonumber$$

We see that adding each term takes the sum closer and closer to the number $2$. More precisely, adding a term $a_n$ to the partial sum $a_1+\dots+a_{n-1}$ cuts the distance between $2$ and $a_1+\dots+a_{n-1}$ in half. For this reason we can, in fact, get arbitrarily close to $2$, so that it is reasonable to expect that

$$1+ \dfrac 1 2+ \dfrac 1 4+ \dfrac 1 8+\dfrac 1 {16}+ \dots =2 \nonumber$$

In the next definition and observation, this equation will be justified and made more precise. We start by providing the definition of an infinite series.

Definition: Infinite Series

An infinite series is given by the

$$\sum_{i=1}^\infty a_i = a_1+a_2+a_3+\dots$$

To be more precise, the infinite sum is defined as the limit $\sum\limits_{i=1}^\infty a_i := \lim\limits_{k\to \infty} \bigg(\sum\limits_{i=1}^k a_i\bigg)$. Therefore, an infinite sum is defined, precisely when this limit exists.

Observation: Infinite Geometric Series

Let $\{a_n\}$ be a geometric sequence with $a_n=a_1\cdot r^{n-1}$. Then the infinite geometric series is defined whenever $-1<r<1$. In this case, we have:

$$\label{EQU:inf-geo-series} \boxed{ \sum_{i=1}^\infty a_i = a_1\cdot \dfrac{1}{1-r} }$$

Proof

Informally, this follows from the formula $\sum_{i=1}^k a_i = a_1\cdot \dfrac{1-r^{k}}{1-r}$ and the fact that $r^k$ approaches zero when $k$ increases without bound.

More formally, the proof uses the notion of limits, and goes as follows:

$$\sum_{i=1}^\infty a_i = \lim_{k\to \infty}\bigg( \sum_{i=1}^k a_i \bigg) = \lim_{k\to \infty}\bigg( a_1\cdot \frac{1-r^{k}}{1-r}\bigg) = a_1\cdot \frac{1-\lim\limits_{k\to\infty } (r^{k})}{1-r} = a_1\cdot \dfrac{1}{1-r} \nonumber$$

Example $\PageIndex{2}$

Find the value of the infinite geometric series.

1. $\sum_{j=1}^\infty a_j$, for $a_j=5\cdot \left(\dfrac 1 3\right)^{j-1}$
2. $\sum_{n=1}^\infty 3\cdot \left(0.71\right)^n$
3. $500-100+20-4+\dots$
4. $3+6+12+24+48+\dots$

Solution

1. We use formula $\ref{EQU:inf-geo-series}$ for the geometric series $a_n=5\cdot \left(\dfrac 1 3\right)^{n-1}$, that is $a_1=5\cdot \left(\dfrac 1 3\right)^{1-1}=5\cdot \left(\dfrac 1 3\right)^{0}=5\cdot 1 =5$ and $r=\dfrac 1 3$. Therefore,

$$\sum_{j=1}^\infty a_j=a_1\cdot \dfrac {1}{1-r}=5\cdot \dfrac {1}{1-\frac 1 3}=5\cdot \dfrac 1 {\frac{3-1}{3}}=5\cdot \dfrac 1 {\frac 2 3}=5\cdot \dfrac 3 2 =\dfrac {15} 2 \nonumber$$

2. In this case, $a_n=3\cdot (0.71)^n$, so that $a_1=3\cdot 0.71^1=3\cdot 0.71=2.13$ and $r=0.71$. Using again formula $\ref{EQU:inf-geo-series}$, we can find the infinite geometric series as

$$\sum_{n=1}^\infty 3\cdot \left(0.71\right)^n=a_1\cdot \dfrac{1}{1-r}=2.13\cdot \dfrac 1 {1-0.71}=2.13\cdot \dfrac 1 {0.29}=\dfrac {2.13}{0.29}=\dfrac{213}{29} \nonumber$$

In the last step we simplified the fraction by multiplying both numerator and denominator by $100$, which had the effect of eliminating the decimals.

3. Our first task is to identify the given sequence as an infinite geometric sequence:

$$\{a_n\} \text{ is given by } 500, -100, 20, -4, \dots \nonumber$$

Notice that the first term is $500$, and each consecutive term is given by dividing by $-5$, or in other words, by multiplying by the common ratio $r=-\dfrac 1 5$. Therefore, this is an infinite geometric series, which can be evaluated as

$$\begin{aligned} 500-100+20-4+\dots &= \sum_{n=1}^\infty a_n\\&=a_1\cdot \dfrac 1 {1-r}\\&=500\cdot \dfrac 1 {1-\left(-\frac 1 5\right)} \\ &= 500 \cdot \dfrac{1}{1+\frac 1 5} \\&=\dfrac {500}{\frac {1+5}{5}}\\&=\dfrac{500}{\frac 6 5}\\&=500\cdot \dfrac 5 6 \\ &= \dfrac {2500}{6} \\&= \dfrac{1250}{3}\end{aligned} \nonumber$$

4. We want to evaluate the infinite series $3+6+12+24+48+\dots$. The sequence $3, 6, 12, 24, 48, \dots$ is a geometric sequence, with $a_1=3$ and common ratio $r=2$. Since $r\geq 1$, we see that formula $\ref{EQU:inf-geo-series}$ cannot be applied, as $\ref{EQU:inf-geo-series}$ only applies to $-1<r<1$. However, since we add larger and larger terms, the series gets larger than any possible bound, so that the whole sum becomes infinite.

$$3+6+12+24+48+\dots=\infty \nonumber$$

Example $\PageIndex{3}$

The fraction $0.55555\dots$ may be written as:

$$0.55555\dots = 0.5+0.05+0.005+0.0005+0.00005+\dots \nonumber$$

Noting that the sequence

$$0.5,\underset{\times 0.1}{\hookrightarrow } 0.05, \underset{\times 0.1}{\hookrightarrow } 0.005, \underset{\times 0.1}{\hookrightarrow } 0.0005, \underset{\times 0.1}{\hookrightarrow } 0.00005, \dots \nonumber$$

is a geometric sequence with $a_1=0.5$ and $r=0.1$, we can calculate the infinite sum as:

$$0.55555\dots = \sum_{i=1}^\infty 0.5 \cdot \left(0.1\right)^{i-1}= 0.5\cdot \dfrac{1}{1-0.1} = 0.5 \cdot\dfrac{1}{0.9}=\dfrac{0.5}{0.9}=\dfrac 5 9 \nonumber$$

Here we multiplied numerator and denominator by $10$ in the last step in order to eliminate the decimals.