Skip to main content
Mathematics LibreTexts

25.1: The Binomial Theorem

  1. Last updated
  2. Save as PDF
  • Page ID
    54484

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Recall the well-known binomial formula:

    \[\boxed{(a+b)^2=a^2+2ab+b^2} \nonumber \]

    \[\text{(since, using ``FOIL,'' we have: } (a+b)^2=(a+b)\cdot (a+b) = a^2+ab+ab+b^2=a^2+2ab+b^2 \text{)} \nonumber \]

    In this section we generalize this to find similar expressions for \((a+b)^n\) for any natural number \(n\). This is the content of the (generalized) binomial theorem below. Before we can state the theorem, we need to define the notion of a factorial and combinations.

    Definition: \(n\) factorial

    For a natural number \(n=1,2,3,\dots\), we define \(n!\) to be the number

    \[\boxed{n! = 1\cdot 2\cdot 3\cdot \dots \cdot n}\]

    The number \(n!\) is called \(n\) factorial.

    To make the formulas below work nicely, we also define \(0!\) to be \(0!=1\).

    It is easy to calculate some examples of factorials.

    Example \(\PageIndex{1}\)

    1. \(4!\)
    2. \(7!\)
    3. \(2!\)

    Solution

    1. \(4 !=1 \cdot 2 \cdot 3 \cdot 4=24\)
    2. \(7 !=1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7=5040\)
    3. \(2 !=1 \cdot 2=2\)

    To calculate factorials with the calculator, we have to use the MATH menu (press \(\boxed{\text{math}}\)), then move to the PRB menu (press \(\boxed{\triangleleft}\)), and use the fourth item (press \(\boxed{\text{4}}\)).

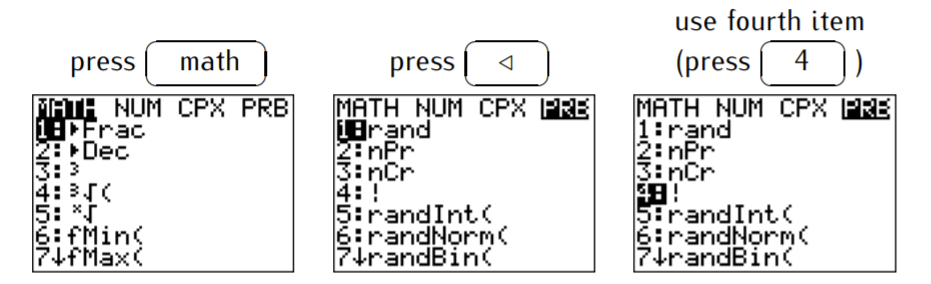
    clipboard_ea9eb3b7bc8b8dd7ccb17cc739dc4921c.png

    For example, we can calculate \(12!=479001600\) by entering \(12\) and the factorial symbol as described above.

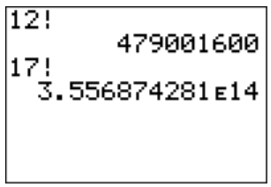
    clipboard_e1f1163298382709468376a9a87ee3548.png

    Note that the factorial becomes very large even for relatively small integers. For example \(17!\approx 3.557\cdot 10^{14}\) as shown above. The next concept that we introduce is that of the binomial coefficient.

    Definition: Binomial Coefficient

    Let \(n=0,1,2,\dots\) and \(r=0,1,2,\dots,n\) be natural numbers or zero, so that \(0\leq r\leq n\). Then we define the binomial coefficient as

    \[\binom{n}{r} = \dfrac{n!}{r!\cdot (n-r)!} \nonumber \]

    The binomial coefficient is also written as \({ }_{n} C_{r}=\dbinom{n}{r}\), and we read them as “\(n\)-choose-\(r\).”

    Note

    • The binomial coefficient \(\dbinom{n}{r}\) should not be confused with the fraction \(\left(\dfrac{n}{r}\right)\).
    • A subset of the set \(\{1,2, \dots, n\}\) with \(r\) elements is called an \(r\)-combination. The binomial coefficient can be interpreted as counting the number of distinct \(r\)-combinations. More precisely, there are exactly \(\dbinom{n}{r}\) distinct \(r\)-combinations of the set \(\{1,\dots, n\}\).

    Example \(\PageIndex{2}\)

    Calculate the binomial coefficients.

    1. \(\dbinom{6}{4}\)
    2. \(\dbinom{8}{5}\)
    3. \(\dbinom{25}{23}\)
    4. \(\dbinom{7}{1}\)
    5. \(\dbinom{11}{11}\)
    6. \(\dbinom{11}{0}\)

    Solution

    1. Many binomial coefficients may be calculated by hand, such as:

    \[\dbinom{6}{4}=\dfrac{6!}{4!(6-4)!}= \dfrac{6!}{4!2!}=\dfrac{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6}{1\cdot 2\cdot 3\cdot 4\cdot 1\cdot 2}=\dfrac{5\cdot 6}{2}=15 \nonumber \]

    1. Again, we can calculate this by hand

    \[\dbinom{8}{5}=\dfrac{8!}{5!3!}=\dfrac{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7 \cdot 8}{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 1\cdot 2 \cdot 3}=\dfrac{6\cdot 7\cdot 8}{1\cdot 2\cdot 3}=7\cdot 8 = 56 \nonumber \]

    However, we can also use the calculator to find the answer. Using the MATH and (press \(\boxed{\text{math}}\)) PRB menus (press \boxed{\triangleleft}\)) as above, we use the third item (press \(\boxed{\text{3}}\)). The answer is obtained by pressing the following sequence of keys:

    \[\begin{array}{|c|c|c|c|}
    \hline 8 & \text { math } & \triangleleft & 3 & 5 & \text { enter } \\
    \hline
    \end{array} \nonumber \]

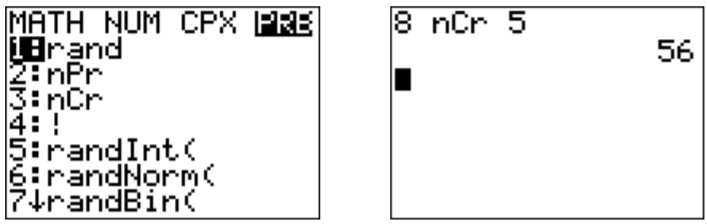
    clipboard_eda469eeb18704e6a502d049f004f3b4a.png

    We also calculate the remaining binomial coefficients (c)-(f), which can also be confirmed with the calculator.

    1. \(\dbinom{25}{23}=\dfrac{25 !}{23 ! \cdot 2 !}=\dfrac{23 ! \cdot 24 \cdot 25}{23 ! \cdot 1 \cdot 2}=\dfrac{24 \cdot 25}{2}=300\)
    2. \(\dbinom{1}{7} = \dfrac{7 !}{1 ! \cdot 6 !}=\dfrac{6 ! \cdot 7}{1 \cdot 6 !}=\dfrac{7}{1}=7\)
    3. \(\dbinom{11}{11} = \dfrac{11 !}{11 ! \cdot 0 !}=\dfrac{1}{1 \cdot 1}=1\)
    4. \(\dbinom{11}{0} = \dfrac{11 !}{0 ! \cdot 11 !}=\dfrac{1}{1 \cdot 1}=1\)

    Note that in the last two equations we needed to use the fact that \(0!=1\).

    We state some useful facts about the binomial coefficient, that can already be seen in the previous example.

    Observation: Binomial Coefficient

    For all \(n=0,1,2,\dots\) and \(r=0, 1, 2, \dots, n\), we have:

    \[\boxed{\dbinom{n}{n-r}=\dbinom{n}{r}} \quad\quad \boxed{\dbinom{n}{0}=\dbinom{n}{n}=1} \quad\quad \boxed{\dbinom{n}{1}=\dbinom{n}{n-1}=n} \nonumber \]

    Proof

    We have:

    \[\begin{aligned} \dbinom{n}{n-r}&=\dfrac{n!}{(n-r)!\cdot (n-(n-r))!}=\dfrac{n!}{(n-r)!\cdot r!}=\dbinom{n}{r} \\ \dbinom{n}{0}&=\dbinom{n}{n}=\dfrac{n!}{0!\cdot n!}=\dfrac{1}{1}=1\\ \dbinom{n}{1}&=\dbinom{n}{n-1}=\dfrac{n!}{1!\cdot (n-1)!}=\dfrac{n}{1}=n\end{aligned} \nonumber \]

    Note

    • We can obtain all binomial coefficients \(\dbinom{n}{r}\) for fixed \(n\) from the calculator by using the function and table menus.

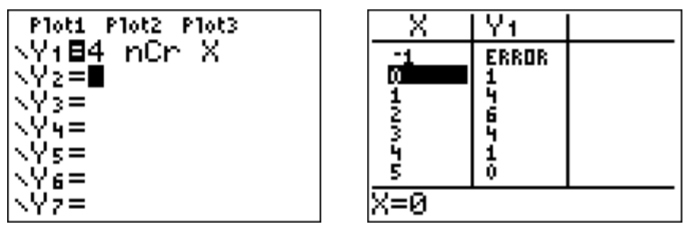
    clipboard_ef9016828d697a33dd4b966d274a3aa90.png

    • The binomial coefficients are found in what is known as Pascal’s triangle. For this, calculate the lowest binomial coefficients and write them in a triangular arrangement:

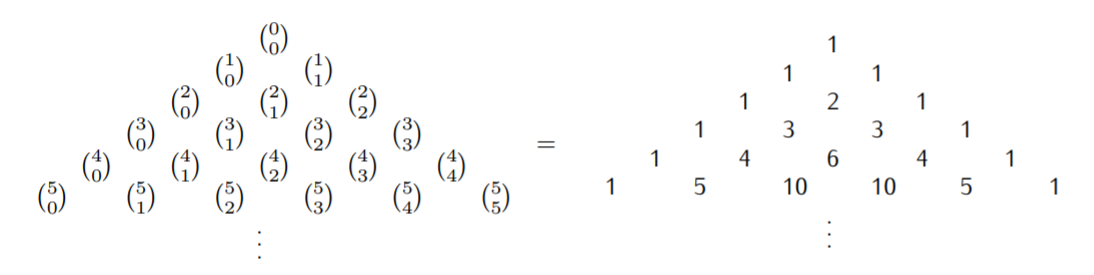
    clipboard_e68beb6035b928031da4c3018e9ca3a3f.png

    The triangle on the right is known as Pascal’s triangle. Each entry in the triangle is obtained by adding the two entries right above it.

    The binomial coefficients appear in the expressions for \((a+b)^n\) as we will see in the next example. We now calculate some simple examples.

    Example \(\PageIndex{3}\)

    \[\begin{aligned} (a+b)^3 &= (a+b)\cdot (a+b)\cdot (a+b)\\ &= (a^2+2ab+b^2)\cdot (a+b)\\ &= a^3+2a^2b+ab^2+a^2b+2ab^2+b^3\\ &= a^3+3a^2b+3ab^2+b^3\end{aligned} \nonumber \]

    Note that the coefficients \(1, 3, 3\), and \(1\) in front of \(a^3, a^2b, ab^2\), and \(b^3\), respectively, are precisely the binomial coefficients \(\dbinom 3 0, \dbinom 3 1, \dbinom 3 2\), and \(\dbinom 3 3\).

    We also calculate the fourth power.

    \[\begin{aligned} (a+b)^4 &= (a+b)\cdot (a+b)\cdot (a+b)\cdot (a+b)\\ &= (a^3+3a^2b+3ab^2+b^3)\cdot (a+b)\\ &= a^4+3a^3b+3a^2b^2+ab^3+a^3b+3a^2b^2+3ab^3+b^4\\ &= a^4+4a^3b+6a^2b^2+4ab^3+b^4\end{aligned} \nonumber \]

    Again, the numbers \(1, 4, 6, 4\), and \(1\) are precisely the binomial coefficients \(\dbinom 4 0, \dbinom 4 1, \dbinom 4 2, \dbinom 4 3\), and \(\dbinom 4 4\).

    We are now ready to state the general binomial theorem.

    Binomial Theorem

    The \(n\)th power \((a+b)^n\) can be expanded as:

    \[(a+b)^n= \dbinom{n}{0} a^n+\dbinom{n}{1} a^{n-1}b^1+\dbinom{n}{2} a^{n-2}b^2+\dots +\dbinom{n}{n-1} a^{1}b^{n-1}+\dbinom{n}{n}b^n \nonumber \]

    Using the summation symbol, we may write this in short:

    \[\boxed{(a+b)^n=\sum_{r=0}^n \dbinom{n}{r} \cdot a^{n-r} \cdot b^{r}} \]

    Example \(\PageIndex{4}\)

    Expand \((a+b)^5\).

    Solution

    \[\begin{aligned} (a+b)^5 &=\dbinom{5}{0} a^5+\dbinom{5}{1} a^{4}b^1+\dbinom{5}{2} a^{3}b^2 +\dbinom{5}{3} a^{2}b^{3}+\dbinom{5}{4} a^1b^{4}+\dbinom{5}{5}b^5 \\ &= a^5+5 a^4b+10 a^3b^2+10 a^2b^3+5ab^4+b^5\end{aligned} \nonumber \]

    This page titled 25.1: The Binomial Theorem is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Thomas Tradler and Holly Carley (New York City College of Technology at CUNY Academic Works) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.