26.3: A.3- Graphing more than one function

Last updated
Save as PDF

Page ID: 54490

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Let us suppose that you want to graph three functions: $y=\sin(360x)$, $y=x$ and $y=x-\dfrac{x^3}{6}$. You would first move the cursor (using the arrow keys) to ’Y1’ enter $\boxed{\sin}$$\boxed{\text{3}}$$\boxed{\text{6}}$$\boxed{\text{0}}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\text{)}}$$\boxed{\text{enter}}$. Note that if you need to clear the field you can use the clear button. Then you would move the cursor to the ’Y2’ position and enter $\boxed{\text{X,T,}\theta,n}$$\boxed{\text{enter}}$. Finally you would move the cursor to the ’Y3’ position and enter $\boxed{\text{X,T,}\theta,n}$$\boxed{\text{-}}$$\boxed{\text{X,T,}\theta,n}$$\boxed{\wedge}$$\boxed{\text{3}}$$\boxed{\triangleright}$$\boxed{\div}$$\boxed{\text{6}}$$\boxed{\text{enter}}$. To graph these functions press $\boxed{\text{graph}}$. The three graphs will be drawn one after the other.

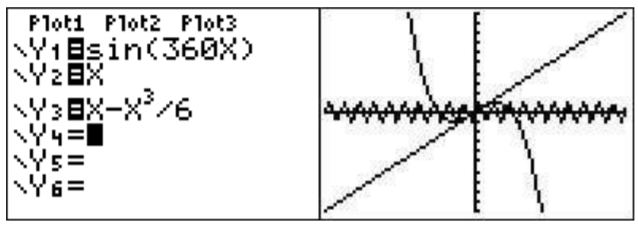
$clipboard_e820e0391876d891ce404a82393169527.png$

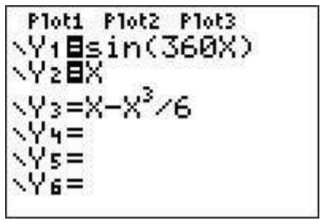
If you would like to just graph the first two but do not want to erase the work you put in to enter the third function, you can move back to the screen and toggle the third function off (or on) by moving the cursor to the ’=’ sign after Y3 and press $\boxed{\text{enter}}$. This equal sign should now be unhighlighted.

$clipboard_e6d85cbfcf1925c3360df1c5bc0199c2f.png$

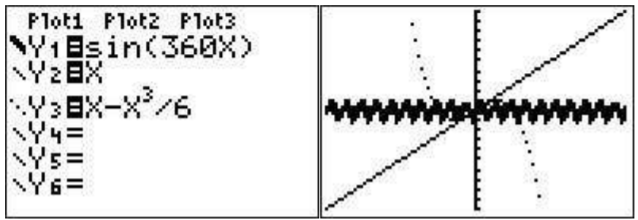
You may also want to have the calculator distinguish between the graphs by the type of line. Let us suppose you want Y1 bold, Y2 normal, and Y3 dashed. Look at the ’to the left of Y1. This is what indicates the type of line. Press $\boxed{\text{enter}}$ until the line type you want is displayed. Move the cursor down and do the same for Y2 and then for Y3.

$clipboard_edd6306cd708d95a1dec4009ea442e3a0.png$

With the help of the Calc menu ($\boxed{\text{2nd}}$$\boxed{\text{trace}}$) you can find the minima of a function, the maxima of a function, intersections of functions, and other similar things. We will describe the intersection feature in detail.

Intersection of functions

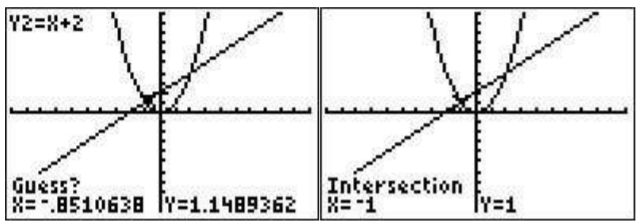
When solving equations graphically, you will want to find the intersection of functions. For example graph $y=x^2$ and $y=x+2$ on the same screen (zoom standard).

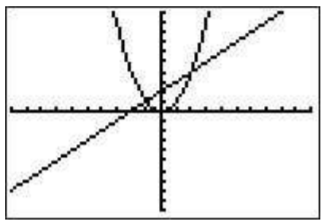
$clipboard_e4ea9a144768b93172ec72c4228b29d5b.png$

To find the left most intersection of the two functions first press $\boxed{\text{2nd}}$$\boxed{\text{trace}}$$\boxed{\text{5}}$. The calculator shows you the graphing screen and will ask you which is the first curve. Move the cursor (using the arrow keys) until it is on the first curve and press $\boxed{\text{enter}}$. It will ask you which is the second curve. Move the cursor to the second curve and press $\boxed{\text{enter}}$.

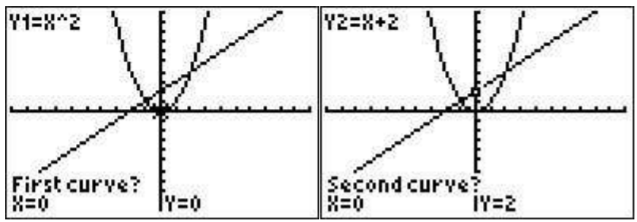
$clipboard_e006e2a5f3f9802a0355d2219161b6f79.png$

It will ask you for a guess. Move the cursor to near the intersection point you want to know and press $\boxed{\text{enter}}$. The intersection will then be displayed.

$clipboard_ee50b290f5131734545bf85d9f5336390.png$