27.2: Review of polynomials and rational functions
- Page ID
- 68483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Divide the polynomials: \(\dfrac{2x^3+x^2-9x-8}{2x+3}\)
- Answer
-
\(x^{2}-x-3+\dfrac{1}{2 x+3}\)
Find the remainder when dividing \(x^3+3x^2-5x+7\) by \(x+2\).
- Answer
-
\(21\)
Which of the following is a factor of \(x^{400}-2x^{99}+1\): \[x-1, \quad x+1, \quad x-0 \nonumber \]
- Answer
-
\(x − 1\) is a factor, \(x + 1\) is not a factor, \(x − 0\) is not a factor
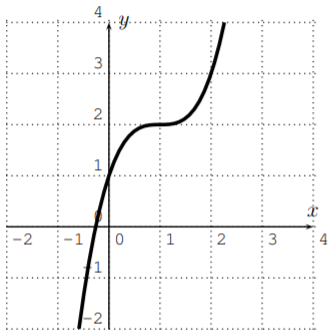
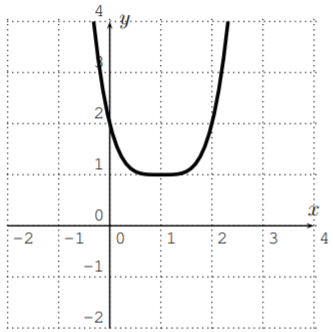
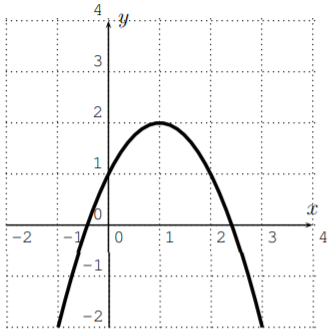
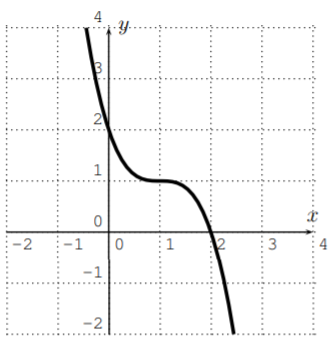
Identify the polynomial with its graph.
- \(f(x)=-x^{2}+2 x+1\) graph: _______________
- \(f(x)=-x^{3}+3 x^{2}-3 x+2\) graph: _______________
- \(f(x)=x^{3}-3 x^{2}+3 x+1\) graph: _______________
- \(f(x)=x^{4}-4 x^{3}+6 x^{2}-4 x+2\) graph: _______________
- Answer
-
- \(\leftrightarrow \text { iii) }\)
- \(\leftrightarrow \text { iv) }\)
- \(\leftrightarrow \mathrm{i})\)
- \(\leftrightarrow \text { ii) }\)
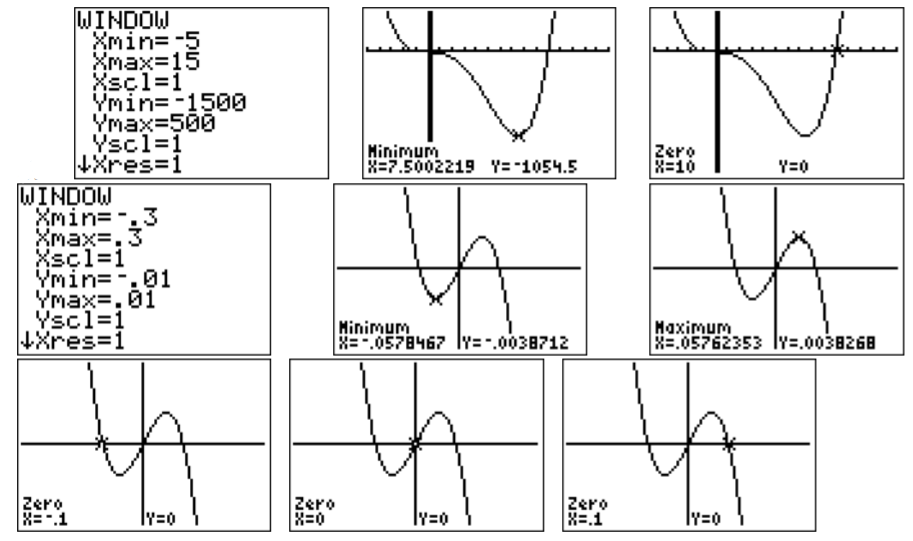
Sketch the graph of the function: \[f(x)=x^4-10x^3-0.01x^2+0.1x \nonumber \]
- What is your viewing window?
- Find all roots, all maxima and all minima of the graph with the calculator.
- Answer
-
Find all roots of \(f(x)=x^3+6x^2+5x-12\).
Use this information to factor \(f(x)\) completely.
- Answer
-
\(f(x)=(x-1)(x+3)(x+4)\)
Find a polynomial of degree \(3\) whose roots are \(0\), \(1\), and \(3\), and so that \(f(2)=10\).
- Answer
-
\(f(x)=(-5) \cdot x(x-1)(x-3)\)
Find a polynomial of degree \(4\) with real coefficients, whose roots include \(-2\), \(5\), and \(3-2i\).
- Answer
-
\(f(x)=(x+2)(x-5)(x-(3-2 i))(x-(3+2 i))\) (other correct answers are possible, depending on the choice of the first coefficient)
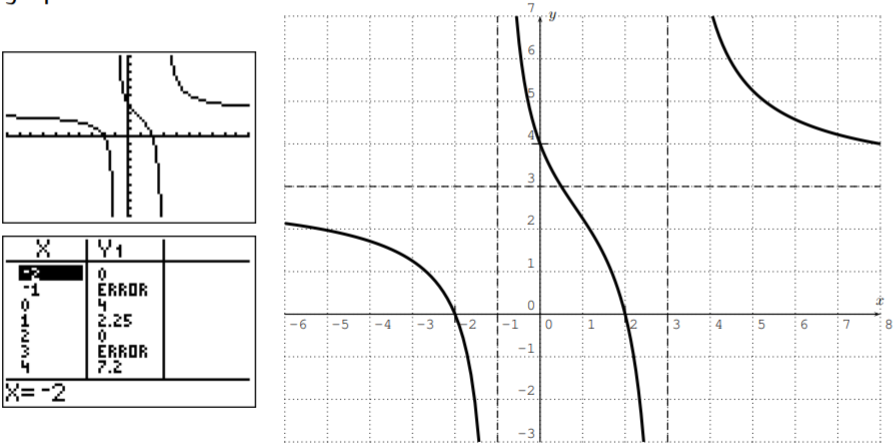
Let \(f(x)=\dfrac{3x^2-12}{x^2-2x-3}\). Sketch the graph of \(f\). Include all vertical and horizontal asymptotes, all holes, and all \(x\)- and \(y\)-intercepts.
- Answer
-
\(f(x)=\dfrac{3(x-2)(x+2)}{(x-3)(x+1)}\) has domain \(D=\mathbb{R}-\{-1,3\}\), horizontal asympt. \(y = 3\), vertical asympt. \(x = −1\) and \(x = 3\), no removable discont., \(x\)-intercepts at \(x = −2\) and \(x = 2\) and \(x = 3\), \(y\)-intercept at \(y = 4\), graph:
Solve for \(x\):
- \(x^4+2x< 2x^3+x^2\)
- \(x^2+3x\geq 7\)
- \(\dfrac{x+1}{x+4}\leq 2\)
- Answer
-
- \((-1,0) \cup(1,2)\)
- \(\left(-\infty, \dfrac{-3-\sqrt{37}}{2}\right] \cup\left[\dfrac{-3+\sqrt{37}}{2}, \infty\right)\)
- \((-\infty,-7] \cup(-4, \infty)\)