7.2: Solving Equations

Introduction

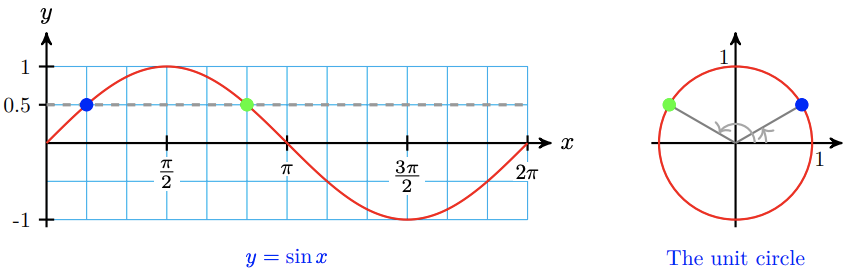
We have seen that an equation of the form \(\sin \theta=k\) (for \(-1<k<1\)) always has two solutions between 0 and \(2 \pi\). For example, the figure below illustrates that \(x=\frac{\pi}{6}\) and \(x=\frac{5 \pi}{6}\) are solutions of the equation \(\sin x=0.5\). These two solutions correspond to the two points on the unit circle where \(y=0.5\).

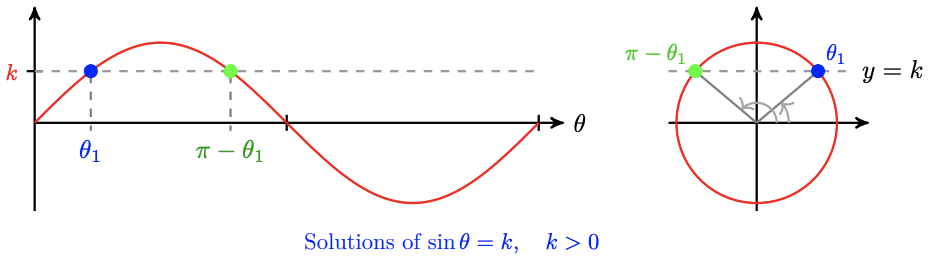
The calculator gives us only one of these solutions, but we can use reference angles to find the other solution. In fact, if we use a calculator to find one solution as \(\theta_1=\sin ^{-1} k\), then the other solution is \(\theta_2=\pi-\theta_1\). You can see this by considering the symmetry of the sine graph, or of the unit circle, as shown below.

This relationship between the two solutions still holds if \(k\) is negative, because the calculator returns a negative angle for \(\theta_1=\sin ^{-1} k\). See the figure below.

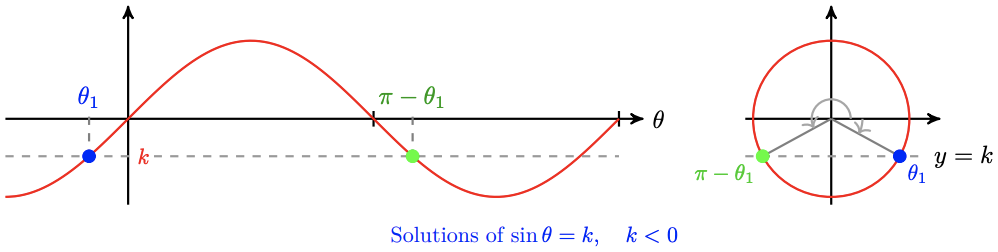
Note 7.25 Why is \(\pi-\theta\) greater than \(\theta\) in the figure above? Think about negative numbers: if \(\theta\) is a negative number, then \(\pi-\theta\) is greater than \(\theta\). For example, if \(\theta=\frac{-\pi}{4}\), then

\(\pi-\theta=\pi-\dfrac{-\pi}{4}=\pi+\dfrac{\pi}{4}=\dfrac{5 \pi}{4}\)

Activity 7.3 Solving Equations.

1 Solutions of \(\sin x=k, k>0\)

a Use your calculator to graph \(y=\sin x\) and \(y=0.6\) in the window

\(\mathrm{Xmin}=0, \quad \mathrm{X} \max =2 \pi, \quad \mathrm{Ymin}=-1.5, \quad \mathrm{Ymax}=1.5\)

b Use the Trace and intersect features to find the smallest solution to \(\sin x=0.6\), accurate to two decimal places.

c Look at the graph, and by symmetry write an expression for the second solution.

Hint: What is the \(x\)-coordinate of the first \(x\)-intercept of \(\sin x\)?

2 Solutions of \(\sin x=k, k<0\)

a Use your calculator to graph \(y=\sin x\) and \(y=-0.6\) in the window

\(\mathrm{Xmin}=0, \quad \mathrm{X} \max =2 \pi, \quad Y \min =-1.5, \quad \mathrm{Ymax}=1.5\)

b On your graph, locate the solution to \(\sin x=-0.6\) given by \(\sin ^{-1}(-0.6)\).

c Can you write an expression for the second solution similar to the expression you wrote in part (1c)?

3 Solutions of \(\sin n x=k, k<0\)

a Use your calculator to graph \(y=\sin x\) and \(y=0.6\) in the window

\(\mathrm{X} \min =0, \quad \mathrm{X} \max =2 \pi, \quad \mathrm{Ymin}=-1.5, \quad \mathrm{Ymax}=1.5\)

b How many solutions are there to the equation \(\sin 2 x=0.6\)?

c Look at the first two solutions. How are they related to the solutions of \(y= \sin x=0.6\) that you found in part (1)? Test your conjecture by using the Trace and intersect features.

d If you know the first two solutions of \(\sin 2 x=0.6\), how can you find the other solutions? Hint: What is the period of \(y=\sin 2 x\)?

4 Solutions of \(\cos n x=k\)

a Repeat part (1) for \(y=\cos x\) and \(y=0.6\).

b Repeat part (2) for \(y=\cos x\) and \(y=-0.6\).

c Repeat part (3) for \(y=\cos 2 x\) and \(y=0.6\).

Example 7.26

Solve \(\sin \theta=-0.58\) for \(0 \leq \theta<2 \pi\).

Answer

The calculator gives us the solution

\(\sin ^{-1}(-0.58)=-0.6187\)

However, because this solution is not between 0 and \(2 \pi\), we find a coterminal angle,

\(\theta_1=\sin ^{-1}(-0.58)+2 \pi=-0.6187+2 \pi=5.6645\)

for the solution in the fourth quadrant. The second quadrant solution is

\(\theta_2=\pi-\sin ^{-1}(-0.58)=\pi+0.6187=3.7603\)

To four decimal places, the desired solutions are 3.7603 and 5.6645.

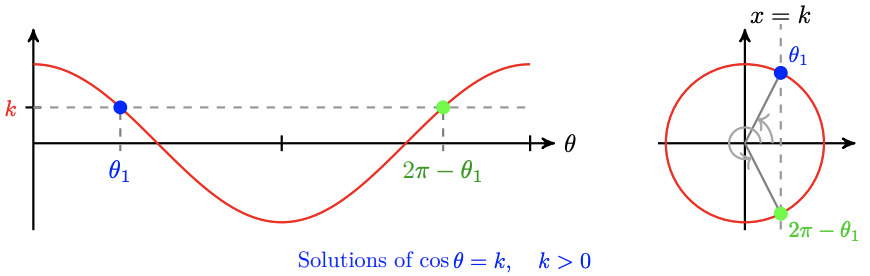
A similar method applies to equations of the form \(\cos \theta=k\). The two solutions between 0 and \(2 \pi\) are \(\theta_1=\cos ^{-1}(k)\) and \(\theta_2=2 \pi-\cos ^{-1}(k)\). Once again, you can see this by considering the symmetry of the cosine graph, or of the unit circle, as shown below

The relationship between the two solutions still holds if \(k\) is negative. See the figure below.

Checkpoint 7.27

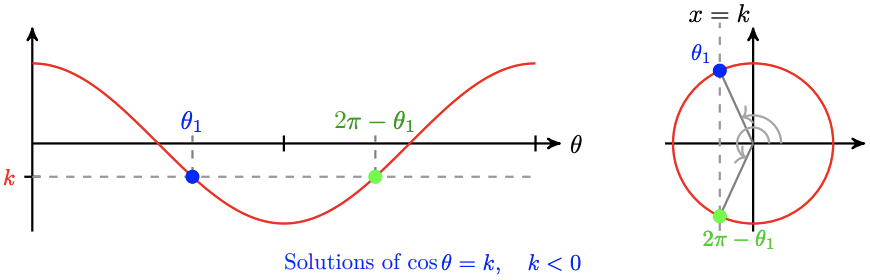
Solve \(\cos \theta=-0.36\) for \(0 \leq \theta<2 \pi\).

Answer

1.9391, 4.3441

Equations of the form \(\tan \theta=k\) are generally easier to solve, because there is only one solution in each cycle of the graph. Each solution differs from the previous one by \(\pi\), as shown below.

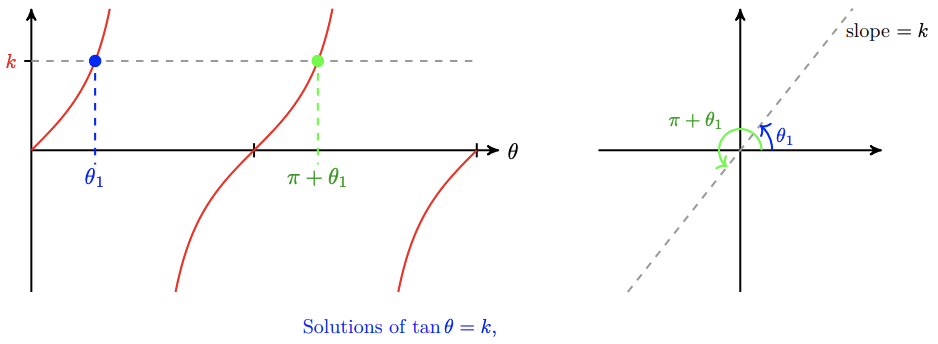
For example, to solve the equation \(\tan \theta=-2.4\) for \(0 \leq \theta<2 \pi\), we first calculate

\(\tan ^{-1}(-2.4)=-1.1760\)

Because this angle is not between 0 and \(2 \pi\), we add \(\pi\) to find the next two solutions:

\begin{aligned}
& \theta_1=-1.1760+\pi=1.9656 \\
& \theta_2=1.9656+\pi=5.1072
\end{aligned}

We summarize these observations for the three trigonometric functions as follows.

Solutions of Trigonometric Equations.

1 The equation \(\cos \theta=k, \quad-1<k<1\), has two solutions between 0 and \(2 \pi\):

\(\theta_1=\cos ^{-1}(k) \text { and } \theta_2=2 \pi-\theta_1\)

2 The equation \(\sin \theta=k, \quad-1<k<1\), has two solutions between 0 and \(2 \pi\):

If \(k>0: \quad \theta_1=\sin ^{-1}(k)\) and \(\theta_2=\pi-\theta_1\)

If \(k<0: \quad \theta_1=\sin ^{-1}(k)+2 \pi\) and \(\theta_2=\pi-\sin ^{-1}(k)\)

3 The equation \(\tan \theta=k\), has two solutions between 0 and \(2 \pi\):

If \(k>0: \theta_1=\tan ^{-1}(k)\) and \(\theta_2=\pi+\theta_1\)

If \(k<0: \quad \theta_1=\tan ^{-1}(k)+\pi\) and \(\theta_2=\pi+\theta_1\)

Multiple Solutions

If \(n\) is an integer, what can we say about the solutions of the equation

\(\sin n x=k ?\)

For example, how many solutions are there for the equation \(\sin 2 x=0.5\)? The figure below shows that this equation has four solutions between 0 and \(2 \pi\). The graph of \(y=\sin 2 x\) completes two cycles between 0 and \(2 \pi\), and each cycle produces two solutions, for a total of four.

Example 7.28

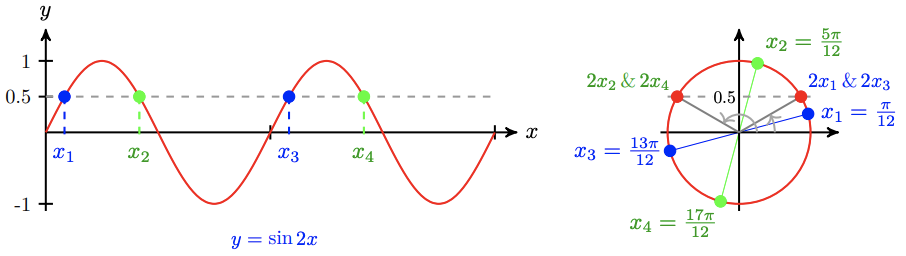
Find all solutions of \(\sin 2 x=0.5\) between 0 and \(2 \pi\).

Answer

We begin as usual, by taking the inverse sine of each side of the equation, to get

\(2 x=\sin ^{-1}(0.5)\)

There are two values of \(2 x\) between 0 and \(2 \pi\) with \(\sin 2 x=0.5\) namely \(2 x=\frac{\pi}{6}\) and \(2 x= \pi-\frac{\pi}{6}=\frac{5 \pi}{6}\). Solving these equations for \(x\) yields \(x=\frac{\pi}{12}\) and \(x=\frac{5 \pi}{12}\).

But these are only two of the four solutions! The graph of \(y=\sin 2 x\) completes two cycles between 0 and \(2 \pi\), each of length \(\pi\). We must add \(\pi\) to each of the first two solutions to find the solutions in the second cycle. These two solutions are

\(\dfrac{\pi}{12}+\pi=\dfrac{13 \pi}{12} \text { and } \dfrac{5 \pi}{12}+\pi=\dfrac{17 \pi}{12}\)

Note that the solutions in the second cycle are still less than \(2 \pi\), so they must be included in the set of all solutions between 0 and \(2 \pi\). The four solutions are \(\frac{\pi}{12}, \frac{5 \pi}{12}, \frac{13 \pi}{12}\) and \(\frac{17 \pi}{12}\).

Checkpoint 7.29

a Sketch a graph of \(y=\cos 2 x\) for \(0 \leq \theta \leq 2 \pi\).

b Find exact values for all solutions of \(\cos 2 x=\frac{-\sqrt{2}}{2}\) between 0 and \(2 \pi\).

Answer

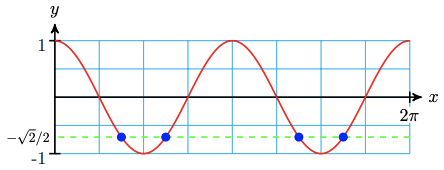
b \(\dfrac{3 \pi}{8}, \dfrac{5 \pi}{8}, \dfrac{11 \pi}{8}, \dfrac{13 \pi}{8}\)

As we observed earlier, equations involving the tangent function are easier to solve, because there is only one solution in each cycle of the graph. Once we have found one solution, we can find all the others by adding multiples of the period.

Example 7.30

Find all solutions of \(\tan 2 t=-1\) between 0 and \(2 \pi\).

Answer

We expect to find four solutions between 0 and \(2 \pi\). The first angle \(2 t\) between 0 and \(2 \pi\) whose tangent is 1 is \(2 t=\frac{3 \pi}{4}\), so the first solution is \(t_1=\frac{3 \pi}{8}\). Now, the period of the graph of \(y=\tan 2 t\) is \(\frac{\pi}{2}\), as shown below.

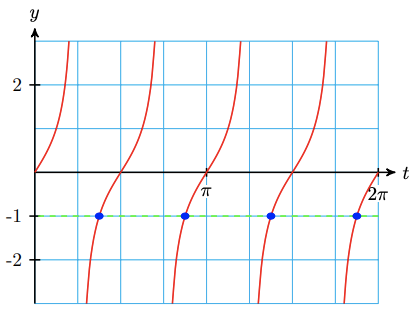
There is one solution in each cycle, so we add multiples of \(\frac{\pi}{2}\) to \(t_1\) to find the other solutions.

\begin{aligned}
t_2 & =\dfrac{3 \pi}{8}+\dfrac{\pi}{2}=\dfrac{7 \pi}{8} \\
t_3 & =\dfrac{7 \pi}{8}+\dfrac{\pi}{2}=\dfrac{11 \pi}{8} \\
t_4 & =\dfrac{11 \pi}{8}+\dfrac{\pi}{2}=\dfrac{15 \pi}{8}
\end{aligned}

The four solutions are \(\frac{3 \pi}{8}, \frac{7 \pi}{8}, \frac{11 \pi}{8}\) and \(\frac{15 \pi}{8}\).

Checkpoint 7.31

Find all solutions of \(\tan 2 x=\sqrt{3}\) between 0 and \(2 \pi\).

Answer

\(\dfrac{\pi}{6}, \dfrac{2 \pi}{3}, \dfrac{7 \pi}{6}, \dfrac{5 \pi}{3}\)

The larger the value of \(n\), the more cycles the graph completes between 0 and \(2 \pi\), and the more solutions we find. Thus, for \(-1<k<1\), there are \(\operatorname{six}\) solutions of \(\sin 3 x=k\) between 0 and \(2 \pi\), eight solutions of \(\sin 4 x=k\), and so on. (See the figure below.)

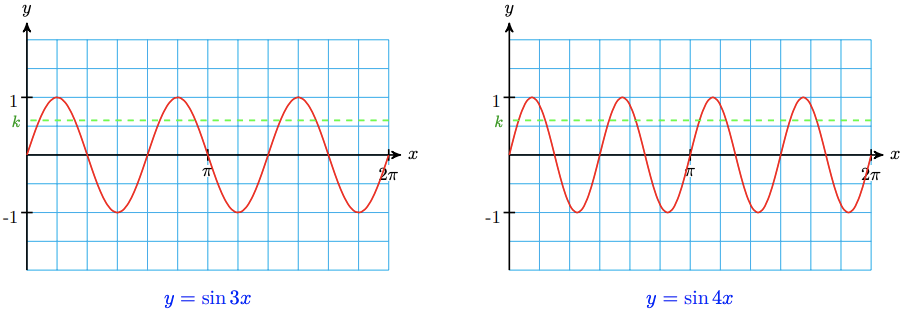
Using a Calculator for Multiple Solutions

Of course, if \(k\) is not one of the special values, we'll need a calculator to help us solve the equation.

Example 7.32

Solve \(1+4 \cos 2 x=2\) for \(0 \leq x \leq 2 \pi\).

Answer

We first solve for the trig ratio, \(\cos 2 x\)

\begin{aligned}
1+4 \cos 2 x & =2 \quad \quad &&\text{Subtract 1 from both sides.}\\
4 \cos 2 x & =1 &&\text{Divide both sides by 4.}\\
\cos 2 x & =0.25
\end{aligned}

Next, we use a calculator to find two solutions of \(\cos 2 x=0.25\). The solutions of this equation, rounded to three decimal places, are

\(\begin{array}{lll}
2 x=1.318 \quad \quad & \text { and } \quad \quad& 2 x=4.965 \\
x_1=0.659 & & x_2=2.483
\end{array}\)

Finally, because the period of the function \(f(x)=\cos 2 x\) is \(\pi\), we can find the other two solutions by adding \(\pi\) to the first two solutions, to get

\begin{aligned}
& x_3=0.659+\pi=3.801 \\
& x_4=2.483+\pi=5.624
\end{aligned}

To two decimal places, the four solutions are 0.66, 2.48, 3.80, and 5.62

Checkpoint 7.33

Solve \(5-2 \sin 3 x=3.7\) for \(0 \leq x \leq 2 \pi\).

Answer

0.24, 1.86, 2.33, 2,95, 4.43, 6.06

Using a Substitution

For more complicated equations, it can be helpful to use a substitution, in order to reduce the equation to the form \(\sin \theta=k\) (or \(\cos \theta=k\) or \(\tan \theta=k\)). We want our substitution to replace the input of the sine function by a single variable. For example, in the next example, we substitute \(\theta\) for the angle \(2 x+1.5\), so that the equation \(\sin (2 x+1.5)=-0.3\) becomes \(\sin \theta=-0.3\).

Example 7.34

Use a substitution to solve \(\sin (2 x+1.5)=-0.3\) for \(0 \leq x \leq 2 \pi\).

Answer

We expect to find four solutions. Let \(\theta=2 x+1.5\), and use a calculator to find two solutions of \(\sin \theta=-0.3\). The solutions, rounded to three decimal places, are

\(\theta_1=\sin ^{-1}(-0.3)=-0.3047 \text { and } \theta_2=\pi-\sin ^{-1}(-0.3)=3.4463\)

Because \(\theta\) is not between 0 and \(2 \pi\), we find a coterminal angle,

\(\theta_1=\sin ^{-1}(-0.3)+2 \pi=5.9785\)

Next we replace \(\theta\) by \(2 x+1.5\) to find two of the solutions of the original equation:

\begin{aligned}
& 2 x+1.5=3.4463 \quad \quad \text { and } \quad \quad &&2 x+1.5=5.9785 \\
& x_1=0.9731 && x_2=2.2392 \\
\end{aligned}

Finally, because the period of the function \(f(x)=\sin (2 x+1.5)\) is \(\pi\), we find the other two solutions by adding \(\pi\) to the first two solutions, to get

\begin{aligned}
x_3 &= 0.9731 + \pi = 4.1147 \\
x_4 &=2.2392 + \pi = 5.3808
\end{aligned}

Rounded to hundredths, the four solutions are 0.97, 2.24, 4.11, and 5.38.

Checkpoint 7.35

Use a substitution to solve \(4 \cos (3 x-0.5)=-3.2\) for \(0 \leq x \leq 2 \pi\).

Answer

1.00, 1.43, 3.09, 3.52, 5.19, 5.62

Here is our strategy for solving trigonometric equations by using a substitution.

Using a Substitution to Solve Trigonometric Equations.

To solve the equation \(\sin (B x+C)=k\) or \(\cos (B x+C)=k\):

1 Substitute \(\theta=B x+C\), and find two solutions for \(\sin \theta=k\) or \(\cos \theta=k\).

2 Replace \(\theta\) by \(B x+C\) in each solution, and solve for \(x\).

3 Find the other solutions by adding multiples of \(\frac{2 \pi}{B}\) to the first two solutions.

To solve the equation \(\tan (B x+C)=k\):

1 Substitute \(\theta=B x+C\), and find one solution for \(\tan \theta=k\).

2 Replace \(\theta\) by \(B x+C\) and solve for \(x\).

3 Find the other solutions by adding multiples of \(\frac{\pi}{B}\) to the first solution.

Example 7.36

Find all solutions between 0 and \(2 \pi\) to \(5+0.4 \tan (3 x-0.5)=4.5\).

Answer

The graph of \(f(x)=5+0.4 \tan (3 x-0.5)\) completes six cycles between 0 and \(2 \pi\), so we expect to find six solutions, as illustrated below. We'll use the substitution \(\theta=3 x-0.5\) to reduce the equation to \(5+0.4 \tan \theta)=4.5\). Next, we isolate the trig ratio. Subtract 5 from both sides of the equation, then divide by 0.4.

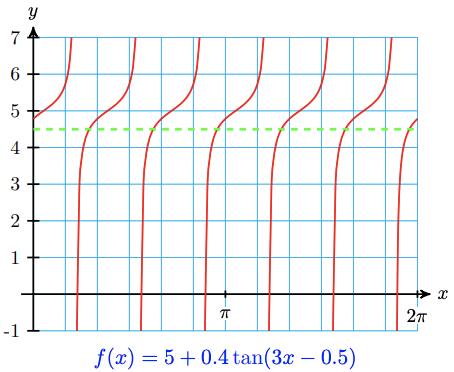
\begin{aligned}
0.4 \tan \theta &= -0.5 \\
\tan \theta &= -1.25
\end{aligned}

Now we can solve for \(\theta\).

\(\theta=\tan ^{-1}(-1.25)=-0.8960\)

Replacing \(\theta\) by \(3x - 0.5\), we find the first solution.

\begin{aligned}
3 x-0.5 & =-0.8960 \\
3 x & =-0.3960 \\
x & =-0.1320
\end{aligned}

This value of \(x\) is not between 0 and \(2\pi\), but because the period of \(f(x)\) is \(\frac{\pi}{3}\), we can add \(\frac{\pi}{3} \approx 1.0472\) to any solution to find another solution.

\begin{aligned}
& x_1=-0.1320+1.0472=0.9152 \\
& x_2=0.9152+1.0472=1.9624 \\
& x_3=1.9624+1.0472=3.0096 \\
& x_4=3.0096+1.0472=4.0568 \\
& x_5=4.0568+1.0472=5.1040 \\
& x_6=5.1040+1.0472=6.1512
\end{aligned}

We stop here, because the next solution is greater than \(2 \pi\). Rounded to two decimal places, the six solutions are 0.92, 1.96, 3.01, 4.06, 5.10, and 6.15.

Checkpoint 7.37

a Graph \(y=2-4 \tan 3(x+0.2) \quad\) from \(x=0\) to \(x=2 \pi\).

b Find all solutions of \(2-4 \tan 3(x+0.2)=5\) between 0 and \(2 \pi\). Round your answers to two decimal places.

Answer

a

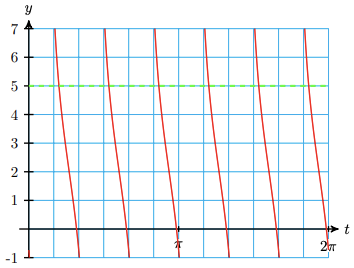
b 0.63, 1.68, 2.73, 3.77, 4.82, 5.87

Applications

Trigonometric equations often arise in the study of periodic models.

Example 7.38

A piston is pumping vertically at a rate of 1000 cycles per second. The distance between its lowest and highest position is 16 centimeters.

a Suppose the piston is at its midline position at \(t=0\) and moving downwards. Find a formula for the sinusoidal function \(h(t)\) that gives the piston's height.

b Use the formula to find the first two times the piston is 14 centimeters above its lowest position.

Answer

a Because the piston starts at its midline and moves down, we will write \(h(y)\) as a sine function:

\(h(t)=-A \sin (B t)+k\)

The amplitude is \(A=\frac{16}{2}=8\), and the midline is \(k=8\). The period is \(\frac{1}{1000}\), so \(\frac{B}{1000}=2 \pi\), and \(B=2000 \pi\).

Thus

\(h(t)=-8 \sin (2000 \pi t)+8\)

The graph is shown below.

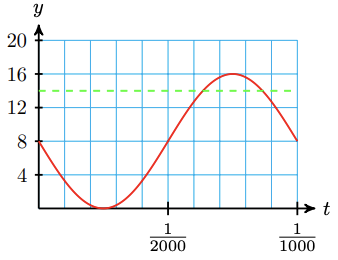
b With \(h(t)=14\), we have

\begin{aligned}
-8 \sin (2000 \pi t)+8 & =14 \quad \quad &&\text{Subtract 8 from both sides.}\\
-8 \sin (2000 \pi t) & =6 &&\text{Divide both sides by -8.}\\
\sin (2000 \pi t) & =\dfrac{-3}{4}
\end{aligned}

We use the substitution \(\theta=2000 \pi t\) and find two positive solutions of the equation \(\sin \theta=\frac{-3}{4}\).

\(\theta=\sin ^{-1}\left(\dfrac{-3}{4}\right) 2 \pi=5.4351 \text { and } \theta=\pi-\sin ^{-1}\left(\dfrac{-3}{4}\right)=3.9897\)

Replace \(\theta\) by \(2000 \pi t\), and solve each equation for \(t\):

\begin{aligned}
& 2000 \pi t=5.4351 \quad \text { and } \quad &&2000 \pi t=3.9897 \\
& t=0.000865 && t=0.000635\\
\end{aligned}

Thus, the first two times the piston is at a height of 14 centimeters are approximately \(t=0.000865\) and \(t=0.000635\) seconds.

Checkpoint 7.39

A lever on an oil well is pumping vertically at a rate of 10 cycles per minute. The distance between its lowest position at the ground and its highest position is 1.8 meters.

a Suppose the lever is at its midline position at \(t=0\) and moving downwards. Find a formula for the sinusoidal function \(h(t)\) that gives the lever's height.

b Find the first two times that lever is 1 meter above its lowest position.

Answer

a \(h(t)=-0.9 \sin (20 \pi t)+0.9\)

b 0.0518 minutes and 0.9823 minutes

Review the following skills you will need for this section.

Algebra Refresher 7.4

Solve.

1 \((2x - 6)^2 = 4\)

2 \(\sqrt{2x-6} = 4\)

3 \(\dfrac{1}{2x-6} = 4\)

4 \(|2x-6| = 4\)

5 \(\log 2x-6 = 4\)

6 \(2^{2x-6} = 4\)

Algebra Refresher Answers

1 2, 4

2 11

3 \(\dfrac{25}{8}\)

4 1, 5

5 5003

6 4

Section 7.3 Summary

Concepts

Solutions of Trigonometric Equations.

1

1 The equation \(\cos \theta = k, \quad -1 < k < 1\), has two solutions between 0 and \(2\pi\):

\(\theta_1=\cos ^{-1}(k)\) and \(\theta_2=2 \pi-\theta_1\)

2 The equation \(\sin \theta=k, \quad-1<k<1\), has two solutions between 0 and \(2 \pi\):

If \(k>0: \theta_1=\sin ^{-1}(k)\) and \(\theta_2=\pi-\theta_1\)

If \(k<0: \quad \theta_1=\sin ^{-1}(k)+2 \pi\) and \(\theta_2=\pi-\sin ^{-1}(k)\)

3 The equation \(\tan \theta=k\), has two solutions between 0 and \(2 \pi\):

If \(k>0: \quad \theta_1=\tan ^{-1}(k)\) and \(\theta_2=\pi+\theta_1\)

If \(k<0: \theta_1=\tan ^{-1}(k)+\pi\) and \(\theta_2=\pi+\theta_1\)

2 If \(n\) is a positive integer, the equations \(\sin n \theta=k\) and \(\cos n \theta=k\) each have \(2 n\) solutions between 0 and \(2 \pi\), for \(-1<k<1\).

3 The equation \(\tan n \theta=k\) has one solution in each cycle of the graph.

4 For more complicated equations, it can be helpful to use a substitution to replace the input of the trig function by a single variable.

Using a Substitution to Solve Trigonometric Equations.

5 To solve the equation \(\sin (B x+C)=k\) or \(\cos (B x+C)=k\):

1 Substitute \(\theta=B x+C\), and find two solutions for \(\sin \theta=k\) or \(\cos \theta=k\).

2 Replace \(\theta\) by \(B x+C\) in each solution, and solve for \(x\).

3 Find the other solutions by adding multiples of \(\frac{2 \pi}{B}\) to the first two solutions.

To solve the equation \(\tan (B x+C)=k\):

1 Substitute \(\theta=B x+C\), and find one solution for \(\tan \theta=k\).

2 Replace \(\theta\) by \(B x+C\) and solve for \(x\).

3 Find the other solutions by adding multiples of \(\frac{\pi}{B}\) to the first solution.

Study Questions

1 If \(x=0.68\) is one solution of the equation \(\cos x=c\), what is other? Illustrate on a unit circle.

2 If \(t=2.45\) is one solution of the equation \(\sin t=k\), what is the other? Illustrate on a unit circle.

3 If \(\theta=1.73\) is one solution of the equation \(\tan \theta=C\), what is the other?

4 Explain why the equation \(\cos n x=k, \quad 0<k<1\), has \(2 n\) solutions between 0 and \(2 \pi\).

Skills

1 Find exact solutions to equations of the form \(\sin n x=k\) #1-10

2 Find all solutions between 0 and \(2 \pi\) #11-16

3 Use a substitution to solve trigonometric equations #17-28

4 Write expressions for exact solutions #29-42

5 Solve problems involving trigonometric models #43-46

Homework 7-3

For Problems 1–10,

a Use a graph to estimate all solutions between 0 and \(2 \pi\).

b Give exact values for the solutions between 0 and \(2 \pi\).

1. \(\sin 4 x=-1\)

2. \(\cos 3 t=0\)

3. \(5 \tan 2 q=0\)

4. \(6 \sin 4 w=-3 \sqrt{2}\)

5. \(4 \cos 3 \phi=-2\)

6. \(\sqrt{3} \tan 2 \alpha=3\)

7. \(2 \sin 2 \beta=1\)

8. \(-6 \cos 2 \theta=6\)

9. \(3 \tan 3 w=\sqrt{3}\)

10. \(2 \tan 3 u=-2\)

For Problems 11-20, find all solutions between 0 and \(2 \pi\). Round your answers to three decimal places.

11. \(9 \cos 2 \theta+1=6\)

12. \(7 \cos 2 t-3=2\)

13. \(8 \tan 4 t+1=-11\)

14. \(3=3 \tan 4 x+4\)

15. \(5 \sin 3 \theta-3=-4\)

16. \(150 \sin 3 s=27\)

17. \(6 \cos 2 r+2=3\)

18. \(2-8 \cos 3 t=-4\)

19. \(\dfrac{5}{7} \tan \pi x+11=11\)

20. \(2 \tan 2 \pi \beta+5=3\)

For Problems 21-28, use a substitution to find exact values for all solutions between 0 and \(2 \pi\).

21. \(2-\tan \left(2 x-\dfrac{\pi}{3}\right)=2\)

22. \(2 \cos \left(3 t+\dfrac{\pi}{4}\right)=\sqrt{3}\)

23. \(6 \cos \left(3 \theta-\dfrac{\pi}{2}\right)=-3 \sqrt{2}\)

24. \(8 \sin \left(2 \theta-\dfrac{\pi}{6}\right)=-4\)

25. \(7 \sin \left(\dfrac{\phi}{2}+\dfrac{3 \pi}{4}\right)+3=-4\)

26. \(3 \tan \left(\dfrac{w}{2}+\dfrac{\pi}{4}\right)+4=1\)

27. \(160 \sin (\pi \phi-1)+10=90\)

28. \(200 \sin \left(\dfrac{t}{\pi}+6\right)-10=-110\)

For Problems 29-42, use a substitution to find all solutions between 0 and \(2 \pi\). Round your answers to hundredths.

29. \(16 \cos (3 t-1)+4=-8\)

30. \(3-5 \cos (2 \phi-1)=6\)

31. \(23-24 \tan (\pi x+2)=17\)

32. \(14 \tan (\pi \beta-4)+31=10\)

33. \(120 \sin \left(\dfrac{\pi}{3}(t-0.2)\right)+21=-3\)

34. \(9 \sin \left(\dfrac{\pi}{2}(t-1)\right)+5=-1\)

35. \(5 \sin \left(3 w-\dfrac{\pi}{3}\right)+1=4\)

36. \(8 \tan \left(4 t-\dfrac{\pi}{3}\right)-24=1\)

37. \(16 \cos \left(\dfrac{\pi}{2}(t+0.3)\right)-7=5\)

38. \(5 \cos \left(\dfrac{\pi}{4}\left(t+\dfrac{1}{4}\right)\right)+3=2\)

39. \(6 \tan \left(\dfrac{\pi}{3}(\theta-1)\right)+4=5\)

40. \(1.5 \sin \left(\dfrac{\pi}{2}(\alpha+0.1)\right)+0.4=0.1\)

41. \(5-3 \cos \left(\dfrac{\pi}{6}(w+0.1)\right)=4\)

42. \(0.34 \cos (2 \pi(\alpha-0.2))=0.085\)

43. The population of deer in Marquette County over the course of a typical year can be approximated by a sinusoidal function. The population reached a maximum of 50,000 deer on September 1, and a minimum of 42,000 deer on March 1.

a Write a formula for the function \(P(t)\) that gives the deer population on the first of each month, where \(t=0\) is September 1.

b When is the deer population 45,000? Give exact expressions and approximations rounded to two decimal places.

c Graph your function over one period, and label the points that correspond to a deer population of 45,000. Is the population greater or less than 45,000 between the two solutions?

44. The percent of the moon visible from earth is a sinusoidal function ranging from \(0 \%\) to \(100 \%\), with a period of 29.5 days.

a Write a formula for the function \(f(t)\) that gives the percent of the moon that is visible, if a new moon (\(0 \%\) visible) occurs at \(t=0\) days.

b When is \(25 \%\) of the moon visible? Give approximations rounded to two decimal places.

c Graph your function over one period, and label the points that correspond to a quarter moon. Is more or less than \(25 \%\) of the moon visible between the two solutions you found in part (b)?

45. A Ferris wheel has a diameter of 20 meters and completes one revolution every 60 seconds. Delbert is at the lowest position of the Ferris wheel, 1 meter above ground, when \(t=0\) seconds.

a Write a formula for the function \(h(t)\) that gives Delbert's altitude in meters after \(t\) seconds.

b When is Delbert at an altitude of 18 meters during his first revolution? Give exact expressions and approximations rounded to two decimal places.

c Graph your function over one period, labeling the points that correspond to an altitude of 18 meters. Is Delbert above or below 18 meters between the two solutions you found in part (b)?

46. High tides occur every 12.2 hours at Point Lookout. The depth of the water at the end of David’s dock is 2.6 meters at high tide and 1.8 meters at low tide.

a Write a formula for the function \(d(t)\) that gives the depth of the water \(t\) hours after last night’s high tide.

b When is the water at the end of the dock 2 meters deep? Give exact approximations rounded to two decimal places.

c Graph your function over one period, labeling the points that correspond to a depth of 2 meters. Is the water depth greater or less than 2 meters between the two solutions you found in part (b)?