9.5: Brokerage
( \newcommand{\kernel}{\mathrm{null}\,}\)
Burt's approach to understanding how the way that an actor is embedded in its neighborhood is very useful in understanding power, influence, and dependency effects. We'll examine some similar ideas in the chapter on centrality. Burt's underlying approach is that of the rational individual actor who may be attempting to maximize profit or advantage by modifying the way in which they are embedded. The perspective is decidedly "neo-classical".
Fernandez and Gould also examined the ways in which actor's embedding might constrain their behavior. These authors, though, took a quite different approach; they focus on the roles that ego plays in connecting groups. That is, Fernandez and Gould's "brokerage" notions examine ego's relations with its neighborhood from the perspective of ego acting as an agent in relations among groups (though, as a practical matter, the groups in brokerage analysis can be individuals).
To examine the brokerage roles played by a given actor, we find every instance where that actor lies on the directed path between two others. So, each actor may have many opportunities to act as a "broker". For each one of the instances where ego is a "broker", we examine which kinds of actors are involved. That is, what are the group memberships of each of the three actors? There are five possible combinations.
In Figure 9.9, the ego who is "brokering" (node B), and both the source and destination nodes (A and C) are all members of the same group. In this case, B is acting as a "coordinator" of actors within the same group as itself.
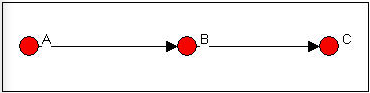
Figure 9.9: Ego B as "coordinator"
In Figure 9.10, ego B is brokering a relation between two members of the same group, but is not itself a member of that group. This is called a "consulting" brokerage role.

Figure 9.10: Ego B as "consultant"
In Figure 9.11, ego B is acting as a gatekeeper. B is a member of a group who is at its boundary, and controls access of outsiders (A) to the group.
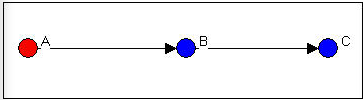
Figure 9.11: Ego B as "gatekeeper"
In Figure 9.12, ego B is in the same group as A, and acts as the contact point or representative of the red group to the blue.
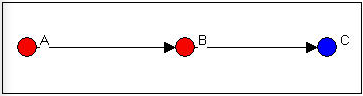
Figure 9.12: Ego B as "representative"
Lastly, in Figure 9.13, ego B is brokering a relation between two groups, and is not part of either. This relation is called acting as a "liaison".
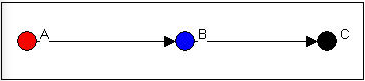
Figure 9.13: Ego B as "liaison"
To examine brokerage, you need to create an attribute file that identifies which actor is part of which group. You can select one of the attributes from a user-created attribute file, or use output files from other UCINET routines that store descriptors of nodes as attributes. As an example, we've taken the Knoke information exchange network, and classified each of the organizations as either a general governmental organization (coded 1), a private non-welfare organization (coded 2), or an organizational specialist (coded 3). Figure 9.14 shows the attribute (or partition) as we created it using the UCINET spreadsheet editor.
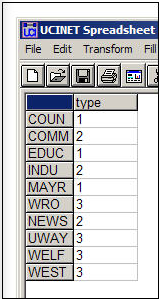
Figure 9.14: Partition vector for Knoke information exchange
Using the network dataset and the attribute vector we just created, we can run Network>Ego Networks>Brokerage, as shown in Figure 9.15.
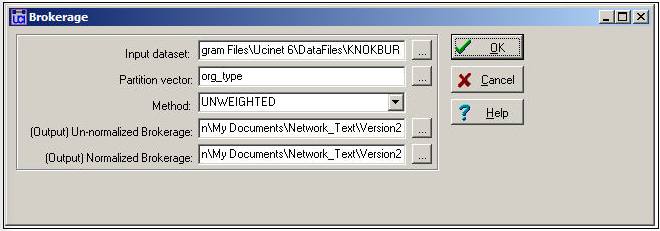
Figure 9.15: Network>Ego Networks>Brokerage dialog box for Knoke information exchange
The option "unweighted" needs a little explanation. Suppose that actor B was brokering a relation between actors A and C, and was acting as a "liaison". In the unweighted approach, this would count as one such relation for actor B. But, suppose that there was some other actor D who also was acting as a liaison between A and C. In the "weighted" approach, both B and D would get 1/2 of the credit for this role; in the unweighted approach, both B and D would get full credit. Generally, if we are interested in ego's relations, the unweighted approach would be used. If we were more interested in group relations, a weighted approach might be a better choice.
The output produced by Network>Ego Networks>Brokerage is quite extensive. We'll break it up into a few parts and discuss them separately. The first piece of the output (Figure 9.16) is a census of the number of times that each actor serves in each of the five roles.
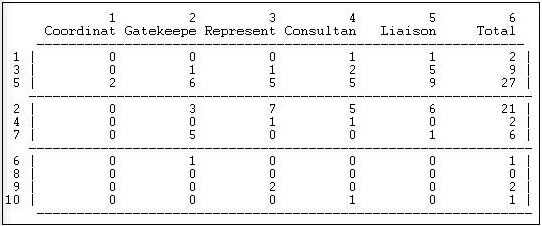
Figure 9.16: Unnormalized brokerage scores for Knoke information network
The actors have been grouped together into "partitions" for presentation; actors 1, 3, and 5, for example, form the first type of organization. Each row counts the raw number of times that each actor plays each of the five roles in the whole graph. Two actors (5 and 2) are the main sources of interconnection among the three organizational populations. Organizations in the third population (6, 8, 9, 10), the welfare specialists, have overall low rates of brokerage. Organizations in the first population (1, 3, 5), the government organizations, seem to be more heavily involved in liaison than other roles. Organizations in the second population (2, 4, 7), non-governmental generalists, play more diverse roles. Overall, there is very little coordination within each of the populations.
We might also be interested in how frequently each actor is involved in relations among and within each of the groups. Figure 9.17 shows these results for the first two nodes.
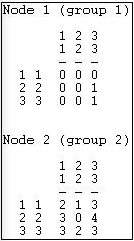
Figure 9.17: Group-to-group brokerage map
We see that actor 1 (who is in group 1) plays no role in connections from group 1 to itself or the other groups (i.e. the zero entries in the first row of the matrix). Actor 1 does, however, act a a "liaison" in making a connection from group 2 to group 3. Actor 1 also acts as a "consultant" in connecting a member of group 3 to another member of group 3. The very active actor 2 does not broker relations within group 2, but is heavily involved in ties in both directions of all three groups to one another, and relations among members of groups 1 and 3.
These two descriptive maps can be quite useful in characterizing the "role" that each ego is playing in the relations among groups by way of their inclusion in its local neighborhood. These roles may help us to understand how each ego may have opportunities and constraints in access to the resources of the social capital of groups as well as individuals. The overall maps also inform us about the degree and form of cohesion within and between the groups.
There may be some danger of "over-interpreting" the information about individuals' brokerage roles as representing meaningful acts of "agency". In any population in which there are connections, partitioning will produce brokerage - even if the partitions are not meaningful, or even completely random. Can we have any confidence that the patterns we are seeing in real data are actually different from a random result?
In Figure 9.18, we see the number of relations of each type that would be expected by pure random processes. We ask: What if actors were assigned to groups as we specify, and each actor has the same number of ties to other actors that we actually observe; but, the ties are distributed at random across the available actors? What if the pattern of roles was generated entirely by the number of groups of various sizes, rather than representing efforts by the actors to deliberately construct their neighborhoods to deal with the constraints and opportunities of group relations?
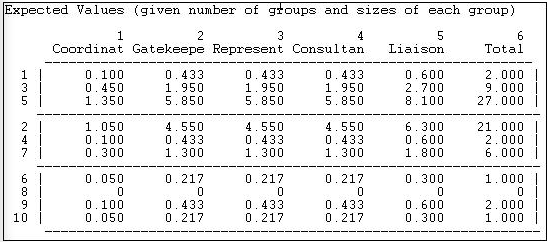
Figure 9.18: Expected values under random assignment
If we examine the actual brokerage relative to this random expectation, we can get a better sense of which parts of which actors' roles are "significant". That is, occur much more frequently that we would expect in a world characterized by groups, but random relations among them.
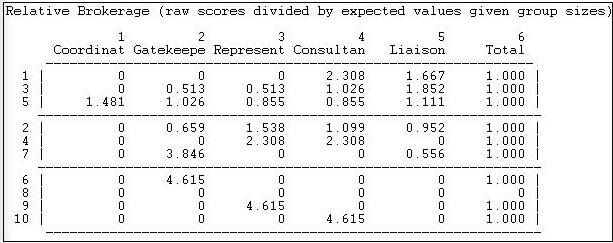
Figure 9.19: Normalized brokerage scores
The normalized brokerage scores in this example need to be treated with a little caution. As with most "statistical" approaches, larger samples (more actors) produce more stable and meaningful results. Since our network does not contain large numbers of relations, and does not have high density, there are many cases where the expected number of relations is small, and finding no such relations empirically is not surprising. Both actor 2 and actor 5, who do broker many relations, do not have profiles that differ greatly from what we would expect by chance. The lack of large deviations from expected values suggests that we might want to have a good bit of caution in interpreting our seemingly interesting descriptive data as being highly "significant".


