13: Pendulum Dynamics
- Page ID
- 93759
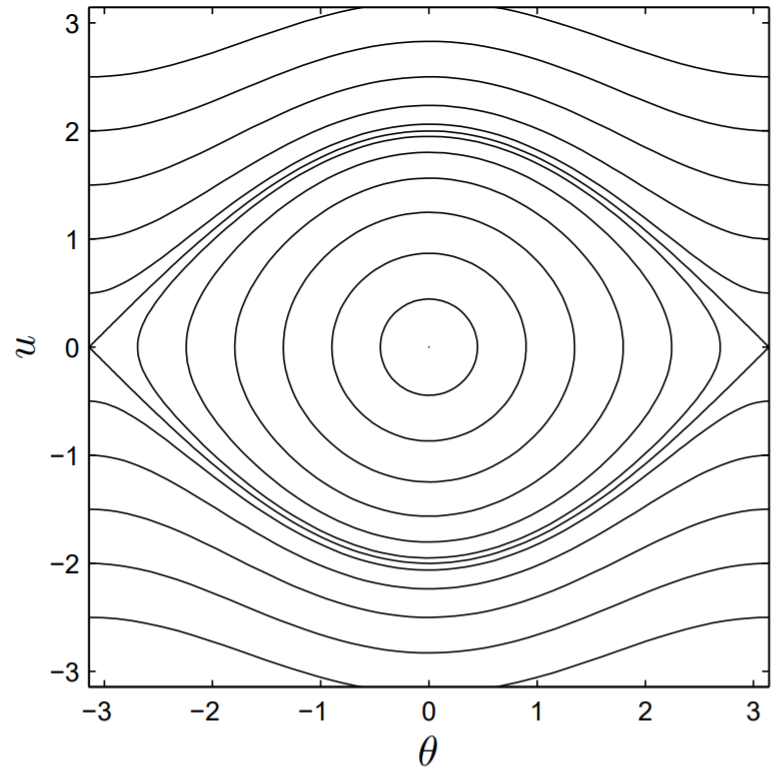
The undriven pendulum has only a two dimensional space, forming a phase plane where it is easy to visualize the phase portraits. The phase portrait of the small amplitude simple pendulum is particularly easy to draw. The dimensionless form of the simple pendulum equation is
\[\ddot{\theta}+\theta=0, \nonumber \]
and the solutions for \(\theta=\theta(t)\) and \(u=\dot{\theta}(t)\) are given by
\[\theta(t)=\theta_{m} \cos (t+\varphi), \quad u(t)=-\theta_{m} \sin (t+\varphi) \nonumber \]
The phase portrait in the \(\theta-u\) phase plane consists of concentric circles, with clockwise motion along these circles, as seen in the small diameter circles of Fig. 13.1. As the amplitude increases, the approximation \(\sin \theta \approx \theta\) loses validity, and the relevant dimensionless equation becomes
\[\ddot{\theta}+\sin \theta=0 . \nonumber \]
Beyond the small diameter circles of Fig. 13.1, one observes that the connected lines become elongated in \(u\) as the amplitude increases, implying the pendulum is slowed down when the amplitude becomes large (i.e., the period of the pendulum is lengthened). Eventually, a final closed curve is drawn, called the separatrix, that separates the pendulum’s motion from periodic to rotary, the latter motion corresponding to a pendulum that swings over the top in a circular motion. Exactly on the separatrix trajectory, the pendulum comes to rest at the angle \(\pi\), or \(180^{\circ}\), which is an unstable fixed point of the pendulum.
The simple pendulum is a conservative system, exhibiting a conservation law for energy, and this implies a conservation of phase space area (or volume). If one evolves over time a given initial area of the phase space of Fig. 13.1, the area of this phase space will be conserved. When the pendulum is damped, however, the area of this phase space will shrink to zero.
Basin of attraction of the undriven pendulum
We consider the damped, undriven pendulum with governing equation
\[\ddot{\theta}+\frac{1}{q} \dot{\theta}+\sin \theta=0 \nonumber \]
and the stable fixed point given by \((\theta, \dot{\theta})=(0,0)\). How can we determine the basin of attraction of this fixed point? Of course, with \(\dot{\theta}=0\), only the values \(-\pi<\theta<\pi\) will lie in the basin of attraction. But we also need to compute the basin of attraction for nonzero initial values of \(\dot{\theta}\).
As is often the case, to devise a numerical algorithm it is best to appeal directly to the physics. We want to find the borderline of initial conditions between either the attractive fixed points \((0,0)\) and \((2 \pi, 0)\), or the attractive fixed points \((0,0)\) and \((-2 \pi, 0)\). The initial conditions just on the border result in the pendulum reaching either the unstable fixed points \((\pi, 0)\) or \((-\pi, 0)\). A small
perturbation from \((\pi, 0)\) will result in one of the attractive points \((0,0)\) or \((2 \pi, 0) ;\) from \((-\pi, 0)\), one of the attractive points \((0,0)\) or \((-2 \pi, 0)\).
The algorithm then initializes the calculation at either the unstable fixed point \((\pi, 0)\) or \((-\pi, 0)\), with a small perturbation in either the position or velocity that results in the final attracting point being \((0,0)\). We can call these values final conditions because the differential equations are then integrated backward in time to determine all possible initial conditions that can result in these final conditions. You can convince yourself that the four final conditions that should be used are the two pairs \((\pi,-\epsilon),(\pi-\epsilon, 0)\), and \((-\pi, \epsilon),(-\pi+\epsilon, 0)\), with \(\epsilon\) very small. The first of each pair corresponds to the immediately previous motion being rotary, and the second of each pair corresponds to the immediately previous motion being oscillatory.
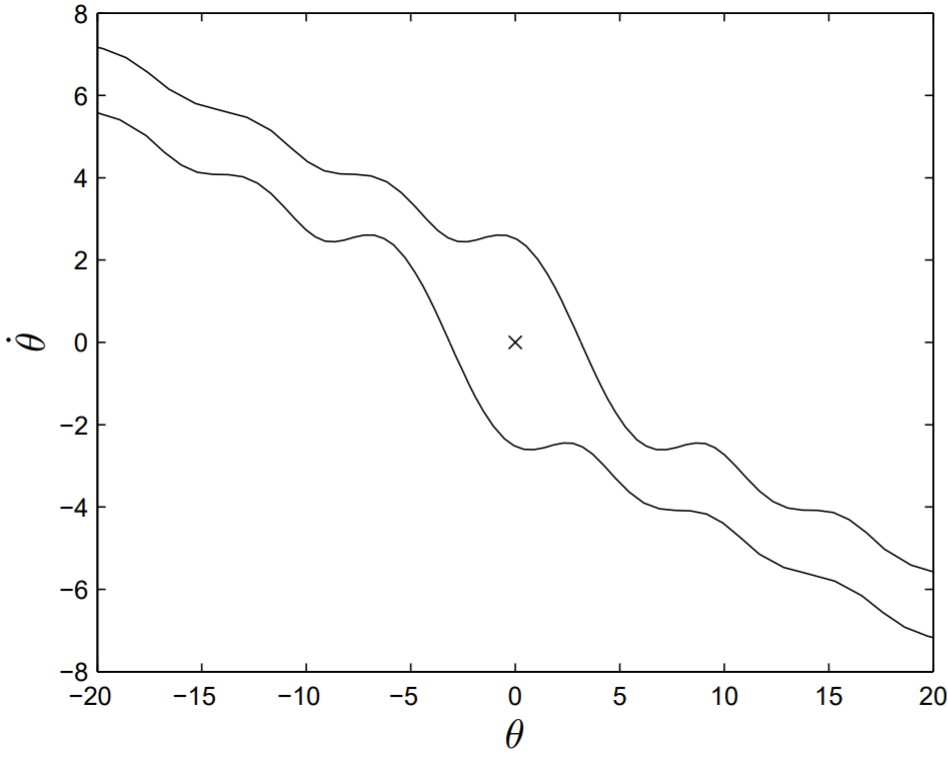
A graph of the basins of attraction of \((0,0)\) for \(q=4\), corresponding to an underdamped pendulum (critical damping is \(q=1 / 2\) ) is shown in Fig. 13.2. The attracting fixed point is marked by an ’ \(x\) ’, and the region inside the two curved lines is the basin of attraction.
Spontaneous symmetry-breaking bifurcation
An interesting supercritical pitchfork bifurcation occurs in the pendulum equations, where at the bifurcation point one stable limit cycle splits into two. The single limit cycle displays a symmetry that is no longer respected individually by the two new limit cycles. This type of pitchfork bifurcation is a manifestation of what is called spontaneous symmetry breaking.
The pendulum equation \((11.14)\), written again here, is given by
\[\ddot{\theta}+\frac{1}{q} \dot{\theta}+\sin \theta=f \cos \omega t . \nonumber \]
Using \(\sin (-\theta)=-\sin \theta\) and \(\cos (\omega t-\pi)=-\cos \omega t\), the pendulum equation can be seen to be invariant under the transformation
\[\theta \rightarrow-\theta, \quad t \rightarrow t-\pi / \omega \nonumber \]
with the physical interpretation that the equations of motion make no distinction between the right and left sides of the vertical, a consequence of the symmetry of both the pendulum and the external force.
Consider again the asymptotic small amplitude solution given by \((11.10)\), which in dimensionless variables is
\[\theta(t)=\frac{f}{\sqrt{\left(1-\omega^{2}\right)^{2}+(\omega / q)^{2}}} \cos (\omega t+\phi), \nonumber \]
with
\[\tan \phi=\frac{\omega / q}{\omega^{2}-1} \nonumber \]
We can observe that this solution is also invariant under \((13.6)\) : the small amplitude solution obeys \(\theta(t)=-\theta(t-\pi / \omega) .\) We say that this solution is symmetric, meaning it obeys the same symmetry as the governing equations; that is, the motion of the small amplitude pendulum is symmetrical about the vertical.
also satisfies (13.5) by the following calculation:
\[\begin{aligned} \ddot{\theta}_{2}(t)+\frac{1}{q} \dot{\theta}_{2}(t)+\sin \left(\theta_{2}(t)\right) &=-\ddot{\theta}_{1}(t-\pi / \omega)-\frac{1}{q} \dot{\theta}_{1}(t-\pi / \omega)-\sin \left(\theta_{1}(t-\pi / \omega)\right) \\ &=-f \cos (\omega t-\pi) \\ &=f \cos \omega t \end{aligned} \nonumber \]
If the two solutions \(\theta_{1}(t)\) and \(\theta_{2}(t)\) are equal, then we say that this solution is symmetric. Here, we are considering asymptotic solutions that are independent of the initial conditions, since the initial conditions themselves can also break the symmetry. However, if \(\theta_{1}(t)\) and \(\theta_{2}(t)\) are not equal, we say that these solutions are asymmetric, and that spontaneous symmetry breaking has occurred. Evidently, spontaneous symmetry breaking is a decidedly nonlinear phenomena. After symmetry breaking occurs, the asymmetric solutions must occur in pairs, and the bifurcation point looks like a pitchfork bifurcation, and can be super- or sub-critical. Any subsequent bifurcation that occurs to one of the asymmetric solutions must also be mirrored by the other.
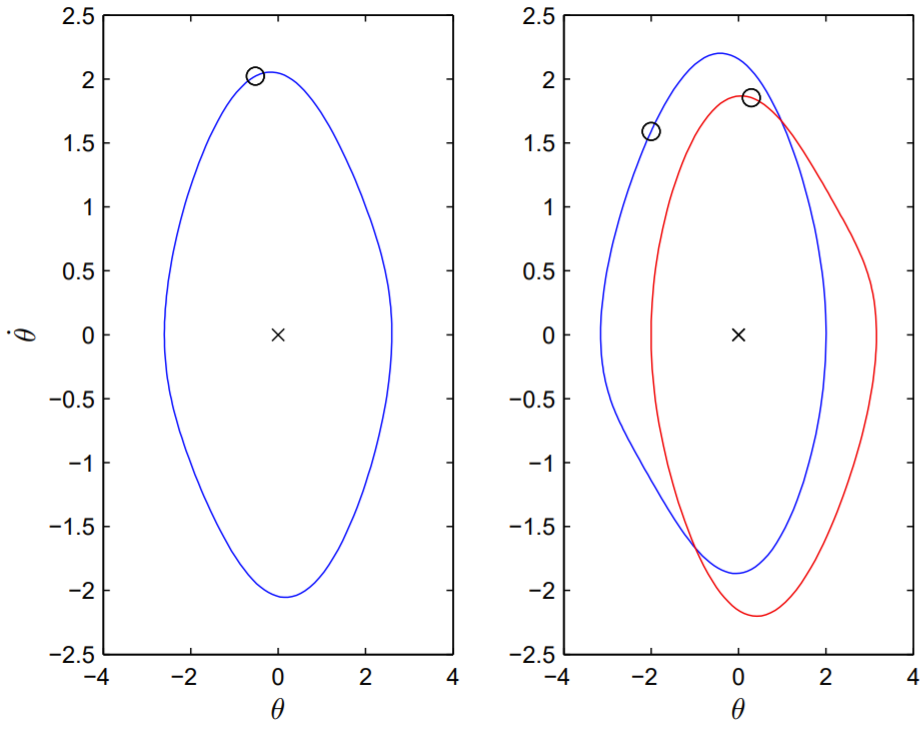
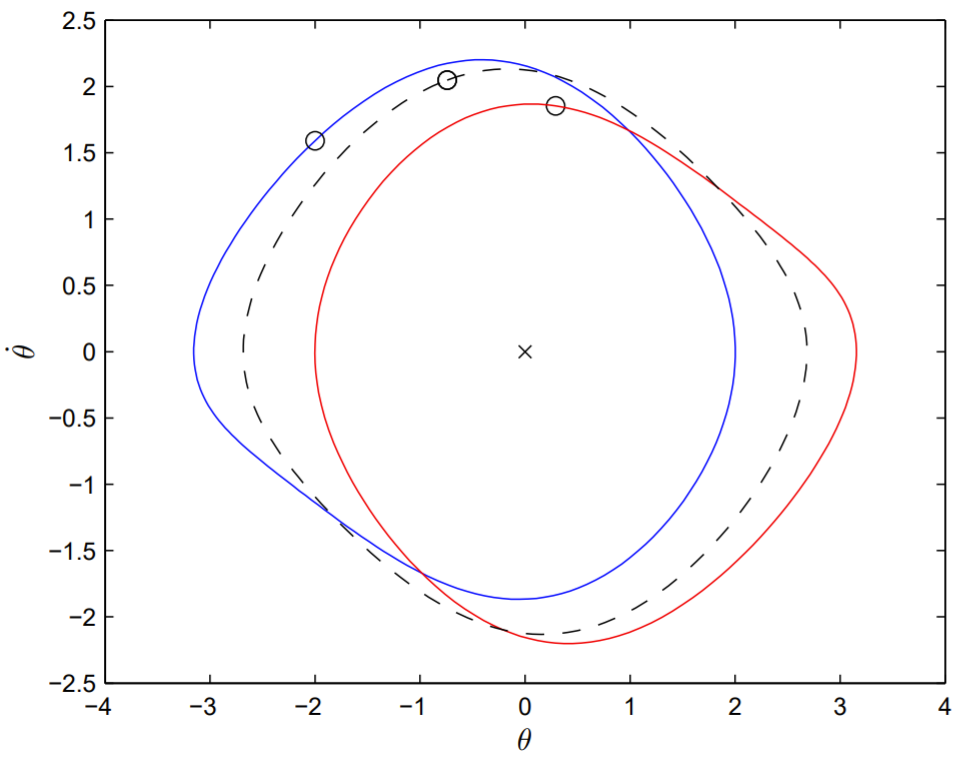
Spontaneous symmetry breaking occurs in the pendulum dynamics at the dimensionless parameter values \(f=1.5, \omega=2 / 3\), and approximately \(q=1.246 .\) For \(q\) just less than \(1.246\), the single stable asymptotic solution for \(\theta=\theta(t)\) is symmetric, and for \(q\) just greater than \(1.246\), there exists a pair of stable asymptotic solutions that are asymmetric.
By projecting the phase-space trajectory onto the \(\theta-\dot{\theta}\) plane, in Fig. \(13.3\) we display both the symmetric solution when \(q=1.24\) and the two asymmetric solutions when \(q=1.30\). To explicitly observe the symmetry of the solutions, we mark the value of \((\theta, \theta)\) at the time \(t=\) \(n 2 \pi / \omega\), with \(n\) a positive integer (equivalent to the time \(t=0)\), and the value of \((-\theta,-\dot{\theta})\) at the time \(t=n 2 \pi / \omega+\pi / \omega\) (equivalent to the time \(t=\pi / \omega\) ). For a symmetric solution, these two points mark the same point on the trajectory, and for asymmetric solutions they mark points on different trajectories. Notice that after the occurrence of symmetry breaking, one of the asymptotic solutions undergoes an oscillation centered to the right of the vertical, and the other, centered to the left.
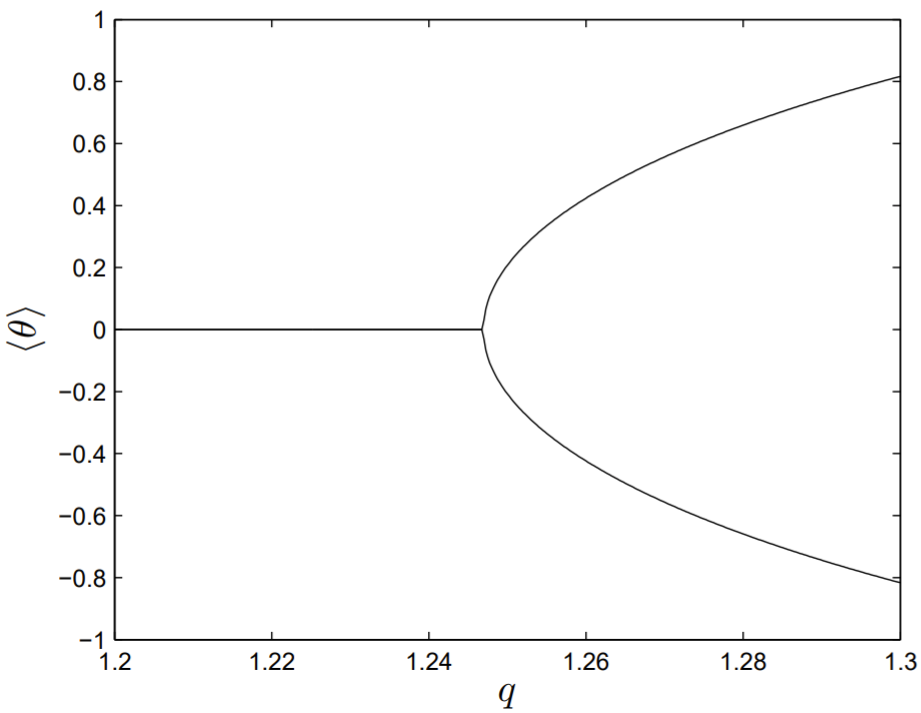
We can graph a bifurcation diagram associated with the symmetry breaking of the solutions. We fix \(f=1.5\) and \(\omega=2 / 3\) and vary \(q\) across the bifurcation point \(q=1.246\). We need to distinguish the symmetric from the asymmetric limit cycles, and one method is to compute the average value of \(\theta(t)\) over one period of oscillation; that is,
\[\langle\theta\rangle=\frac{1}{T} \int_{0}^{T} \theta d t \nonumber \]
where \(T=2 \pi / \omega .\) For the symmetric solution, \(\langle\theta\rangle=0\), whereas \(\langle\theta\rangle\) takes on both positive and negative values after symmetry breaking occurs. In Fig. 13.4, we plot the value of \(\langle\theta\rangle\) versus \(q\). At a value of approximately \(q=1.246\), spontaneous symmetry breaking occurs and the stable symmetric limit cycle splits into two asymmetric limit cycles, in what is evidently a supercritical pitchfork bifurcation.
The symmetric limit cycle still exists after the bifurcation point, and though unstable, can also be computed. To compute the unstable cycle, one could determine the values of \(\theta\) and \(\dot{\theta}\) at \(t=0\) that lie on this cycle, and then integrate over one period (over which the instability doesn’t have sufficient time to develop). The problem of determining the correct initial conditions can be cast as a problem in multidimensional root-finding. The key idea is that a symmetric limit cycle satisfies \(\theta(t)=-\theta(t-\pi / \omega)\). We therefore determine the solution vector of initial conditions \((\theta(0), \theta(0))\) that satisfies the two equations
\[\begin{aligned} &\theta(0)+\theta(\pi / \omega)=0 \\ &\dot{\theta}(0)+\dot{\theta}(\pi / \omega)=0 \end{aligned} \nonumber \]
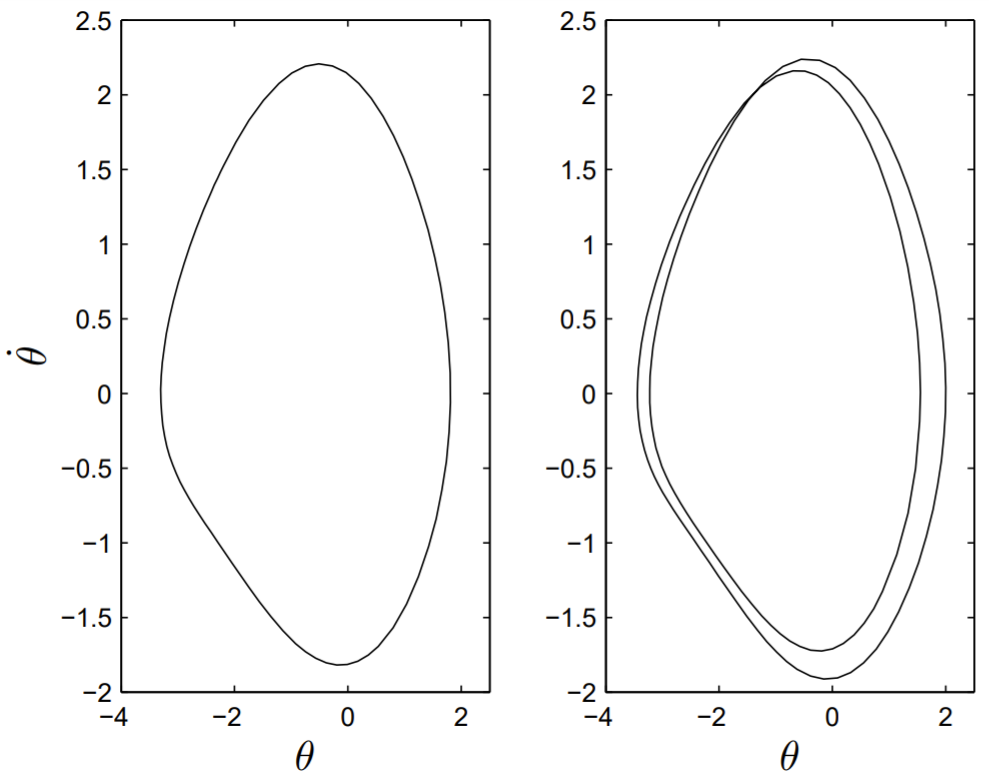
where \(\theta(\pi / \omega)\) and \(\dot{\theta}(\pi / \omega)\) are determined by integrating from \(t=0\) the differential equations using ode \(45 . \mathrm{m}\) with the initial conditions \((\theta(0), \dot{\theta}(0))\). Root-finding can be done using either a two-dimensional version of the secant rule or, more simply, the built-in MATLAB function fsolve.m. Convergence to the roots is robust, and an initial guess for the roots can be taken, for instance, as \((\theta(0), \dot{\theta}(0))=(0,0)\). A plot of the two stable asymmetric limit cycles, and the unstable symmetric limit cycle when \(f=1.5, \omega=2 / 3\) and \(q=1.3\) is shown in Fig. 13.5.
Period-doubling bifurcations
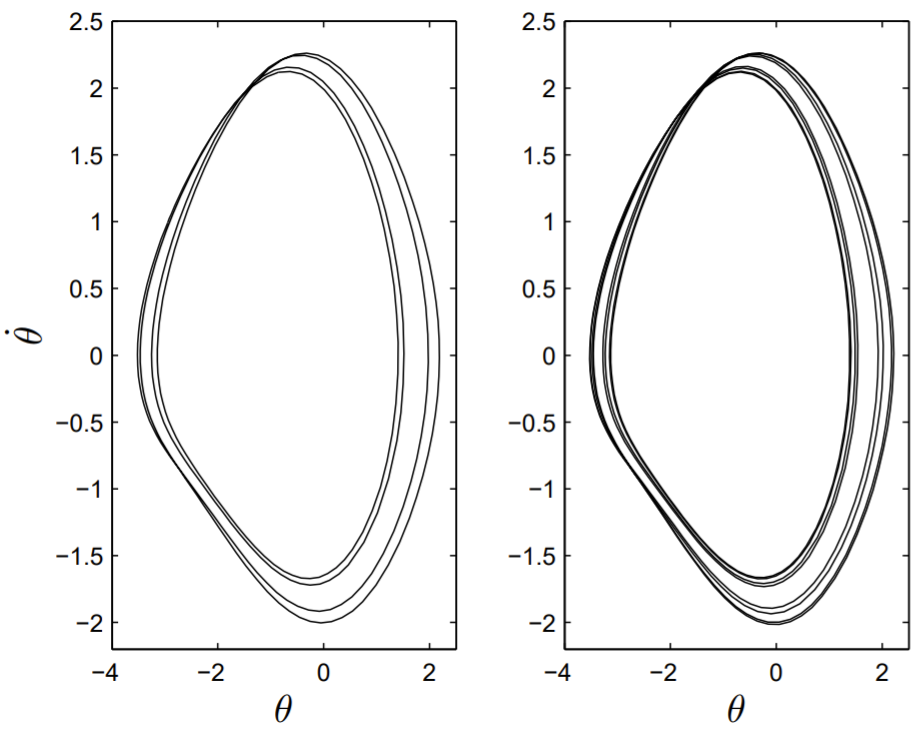
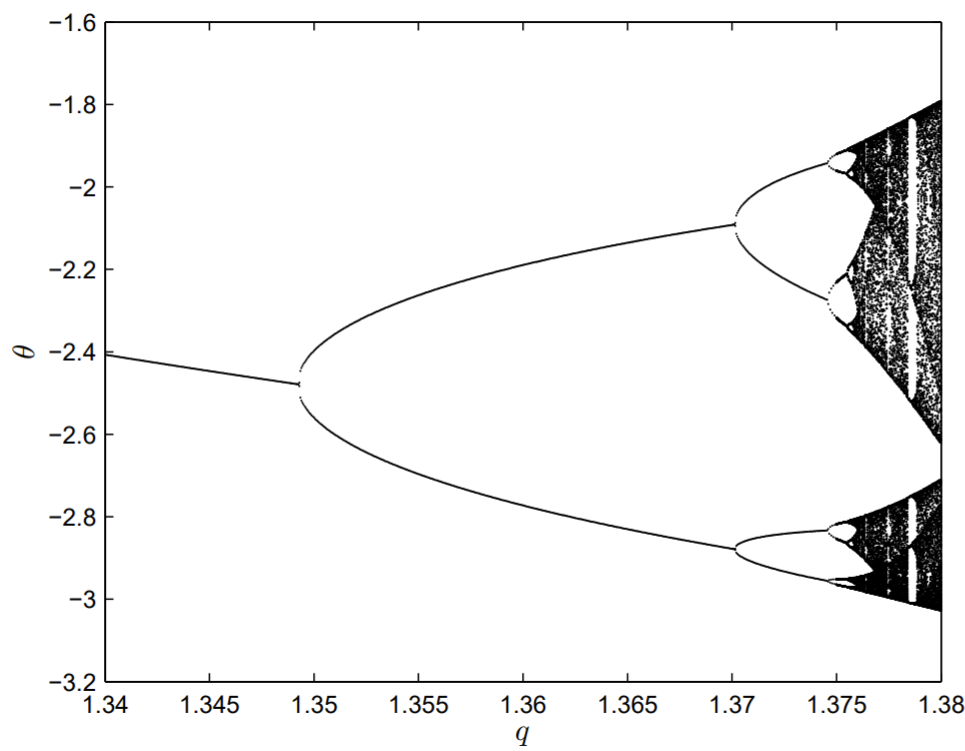
The period-doubling bifurcations continue with increasing \(q\). The second doubling from period two to period four occurs at approximately \(q=1.370\) and the third doubling from period four to period eight occurs at approximately \(q=1.375\). The \(\theta-\dot{\theta}\) phase-space projections for period four and period eight are shown in Fig. 13.8.
A bifurcation diagram can be plotted that illustrates these period-doubling bifurcations. We use a Poincaré section to plot the value of \(\theta\) at the times corresponding to \(2 \pi n / \omega\), with \(n\) an integer. The control parameter for the bifurcation is \(q\), and in Fig. 13.9, we plot the bifurcation diagram for \(1.34<q<1.38\). In general, the angle \(\theta\) should be mapped into the interval \(-\pi<\) \(\theta<\pi\), but for these parameter values there is no rotary motion. Period-doubling bifurcations are observed, and eventually the pendulum becomes aperiodic. Additional windows of periodicity in the aperiodic regions of \(q\) are also apparent.
The aperiodic behavior of the pendulum observed in Fig. \(13.9\) corresponds to a chaotic pendulum. If only the pendulum exhibited the period-doubling route to chaos, then the results shown in Fig. 13.9, though interesting, would be of lesser importance. But in fact many other nonlinear systems also exhibit this route to chaos, and there are some universal features of Fig. \(13.9\), first discovered by Feigenbaum in 1975. One of these features is now called the Feigenbaum constant, \(\delta\)
Note that for the pendulum, we can already compute
\[\delta_{1}=\frac{1.370-1.348}{1.375-1.370}=4.400 \nonumber \]
The meaning of \(\delta\) can be better elucidated by writing
\[q_{n+2}-q_{n+1}=\frac{q_{n+1}-q_{n}}{\delta_{n}} \nonumber \]
and by continuing to iterate this equation, we obtain
\[q_{n+2}-q_{n+1}=\frac{q_{2}-q_{1}}{\delta_{1} \delta_{2} \cdots \delta_{n}} . \nonumber \]
With all the \(\delta_{n}\) ’s approximately equal to \(\delta\), we then have the scaling
\[q_{n+2}-q_{n+1} \propto \delta^{-n} \nonumber \]
A \(\delta\) larger than one would then insure that the bifurcations occur increasingly closer together, so that an infinite period (and chaos) is eventually attained. The value of \(\delta\) can be computed to high accuracy and has been found to be
\[\delta=4.669201609102990 \ldots, \nonumber \]
and our value of \(\delta_{1}=4.4\) is a rough approximation.
Period doubling in the logistic map
Feigenbaum originally discovered the period-doubling route to chaos by studying a simple onedimensional map. A one-dimensional map with a single control parameter \(\mu\) can be written as
\[x_{n+1}=f_{\mu}\left(x_{n}\right) \nonumber \]
where \(f_{\mu}(x)\) is some specified function. A one-dimensional map is iterated, starting with some initial value \(x_{0}\), to obtain the sequence \(x_{1}, x_{2}, x_{3}, \ldots .\) If the sequence converges to \(x_{*}\), then \(x_{*}\) is a stable fixed point of the map.
The specific one-dimensional map we will study here is the logistic map, with
\[f_{\mu}(x)=\mu x(1-x) \nonumber \]
The logistic map is perhaps the simplest nonlinear equation that exhibits the period-doubling route to chaos. To constrain the values of \(x_{n}\) to lie between zero and unity, we assume that \(0<\mu<4\) and that \(0<x_{0}<1\).
A period-1 cycle for the logistic map corresponds to a stable fixed point. Stable fixed points are solutions of the equation \(x=f_{\mu}(x)\), or
\[x=\mu x(1-x) . \nonumber \]
The two solutions are given by \(x_{*}=0\) and \(x_{*}=1-1 / \mu\). The first fixed point \(x_{*}=0\) must be stable for \(0<\mu<1\), being the only fixed point lying between zero and one that exists in this range. To determine the stability of the second fixed point, we make use of the linear stability analysis discussed in \(\S 12.1\).
For a one-dimensional map, \(x_{*}\) is a stable fixed point of \((13.17)\) if \(\left|f_{\mu}^{\prime}\left(x_{*}\right)\right|<1 .\) For the logistic map given by (13.18), \(f_{\mu}^{\prime}(0)=\mu\) so that \(x_{*}=0\) is stable for \(0<\mu<1\) as we have already surmised, and for the second fixed point
\[f_{\mu}^{\prime}(1-1 / \mu)=2-\mu . \nonumber \]
Therefore, we find that \(x_{*}=1-1 / \mu\) is stable for \(1<\mu<3\).
What happens when \(\mu\) becomes larger than three? We will now show that the first perioddoubling bifurcation occurs at \(\mu=3\). Because of the simplicity of the logistic map, we can determine explicitly the period-2 cycle. Consider the following composite map:
\[g_{\mu}(x)=f_{\mu}\left(f_{\mu}(x)\right) \nonumber \]
Fixed points of this map will consist of both period-1 cycles and period-2 cycles of the original map (13.18). If \(x=x_{*}\) is a fixed point of the composite map (13.21), then \(x_{*}\) satisfies the equation
\[x=g_{\mu}(x) \nonumber \]
A period-2 cycle of the map \(f_{\mu}(x)\) necessarily corresponds to two distinct fixed points of the composite map (13.21). We denote these two fixed points by \(x_{0}\) and \(x_{1}\), which satisfy
\[x_{1}=f_{\mu}\left(x_{0}\right), \quad x_{0}=f_{\mu}\left(x_{1}\right) . \nonumber \]
We will call \(x_{0}, x_{1}\) the orbit of the period-2 cycle, with the later generalization of calling \(x_{0}, x_{1}\), \(\ldots, x_{2^{n}}-1\) the orbit of the period \(-2^{n}\) cycle.
The period-2 cycle can now be determined analytically by solving
\[\begin{aligned} x &=f_{\mu}\left(f_{\mu}(x)\right) \\ &=f_{\mu}(\mu x(1-x)) \\ &=\mu(\mu x(1-x))(1-\mu x(1-x)) \end{aligned} \nonumber \]
which is a quartic equation for \(x\). Two solutions corresponding to period-1 cycles are known: \(x_{*}=0\) and \(x_{*}=1-1 / \mu\). Factoring out these two solutions, the second by using long division, results in the quadratic equation given by
\[\mu^{2} x^{2}-\mu(\mu+1) x+(\mu+1)=0 . \nonumber \]
The period-2 cycle, then, corresponds to the two roots of this quadratic equation; that is,
\[x_{0}=\frac{1}{2 \mu}((\mu+1)+\sqrt{(\mu+1)(\mu-3)}), \quad x_{1}=\frac{1}{2 \mu}((\mu+1)-\sqrt{(\mu+1)(\mu-3)}) . \nonumber \]
These roots are valid solutions for \(\mu \geq 3\). Exactly at \(\mu=3\), the period-2 cycle satisfies \(x_{0}=x_{1}=\) \(2 / 3\), which coincides with the value of the period-1 cycle \(x_{*}=1-1 / \mu=2 / 3 .\) At \(\mu=3\), then, we expect the fixed point of the composite map corresponding to a period-1 cycle to go unstable via a supercritical pitchfork bifurcation to a pair of stable fixed points, corresponding to a period-2 cycle.
When does this period-2 cycle become unstable? At \(\mu=3\) and \(x_{*}=2 / 3\), we have
\[\begin{aligned} f_{\mu}^{\prime}\left(x_{*}\right) &=\mu\left(1-2 x_{*}\right) \\ &=-1, \end{aligned} \nonumber \]
so that the period-1 cycle becomes unstable when the derivative of the map function attains the value of \(-1\), and it is reasonable to expect that the period-2 cycle also becomes unstable when
\[g_{\mu}^{\prime}\left(x_{0}\right)=-1, \quad g_{\mu}^{\prime}\left(x_{1}\right)=-1 . \nonumber \]
Now,
\[\begin{aligned} g_{\mu}^{\prime}\left(x_{0}\right) &=f_{\mu}^{\prime}\left(f_{\mu}\left(x_{0}\right)\right) f_{\mu}^{\prime}\left(x_{0}\right) \\ &=f_{\mu}^{\prime}\left(x_{1}\right) f_{\mu}^{\prime}\left(x_{0}\right), \end{aligned} \nonumber \]
and
\[\begin{aligned} g_{\mu}^{\prime}\left(x_{1}\right) &=f_{\mu}^{\prime}\left(f_{\mu}\left(x_{1}\right)\right) f_{\mu}^{\prime}\left(x_{1}\right) \\ &=f_{\mu}^{\prime}\left(x_{0}\right) f_{\mu}^{\prime}\left(x_{1}\right) . \end{aligned} \nonumber \]
The two equations of \((13.26)\) are therefore identical, and the period-2 cycle will go unstable at the value of \(\mu\) satisfying
\[f_{\mu}^{\prime}\left(x_{0}\right) f_{\mu}^{\prime}\left(x_{1}\right)=-1 \nonumber \]
where \(x_{0}\) and \(x_{1}\) are given by (13.25).
The equation for \(\mu\), then, is given by
\[\mu^{2}\left(1-2 x_{0}\right)\left(1-2 x_{1}\right)=-1 \nonumber \]
Or
\[\mu^{2}\left(1-2\left(x_{0}+x_{1}\right)+4 x_{0} x_{1}\right)+1=0 \nonumber \]
Now, from (13.25),
\[x_{0}+x_{1}=\frac{\mu+1}{\mu}, \quad x_{0} x_{1}=\frac{\mu+1}{\mu^{2}} . \nonumber \]
Substitution of (13.30) into (13.29) results, after simplification, in the quadratic equation
\[\mu^{2}-2 \mu-5=0, \nonumber \]
with the only positive solution given by
\[\begin{aligned} \mu &=1+\sqrt{6} \\ & \approx 3.449490 . \end{aligned} \nonumber \]
We therefore expect the period-2 cycle to bifurcate to a period-4 cycle at \(\mu \approx 3.449490\).
CHAPTER 13. PENDULUM DYNAMICS
| \(n\) | \(\mu_{n}\) |
|---|---|
| 1 | 3 |
| 2 | \(3.449490 \ldots\) |
| 3 | \(3.544090 \ldots\) |
| 4 | \(3.564407 \ldots\) |
| 5 | \(3.568759 \ldots\) |
| 6 | \(3.569692 \ldots\) |
| 7 | \(3.569891 \ldots\) |
| 8 | \(3.569934 \ldots\) |
Table 13.1: The first eight values of \(\mu_{n}\) at which period-doubling bifurcations occur.
If we define \(\mu_{n}\) to be the value of \(\mu\) at which the period-2 \(^{n-1}\) cycle bifurcates to a period-2 \(^{n}\) cycle, then we have determined analytically that \(\mu_{1}=3\) and \(\mu_{2}=1+\sqrt{6}\). We list in Table 13.1, the first eight approximate values of \(\mu_{n}\), computed numerically.
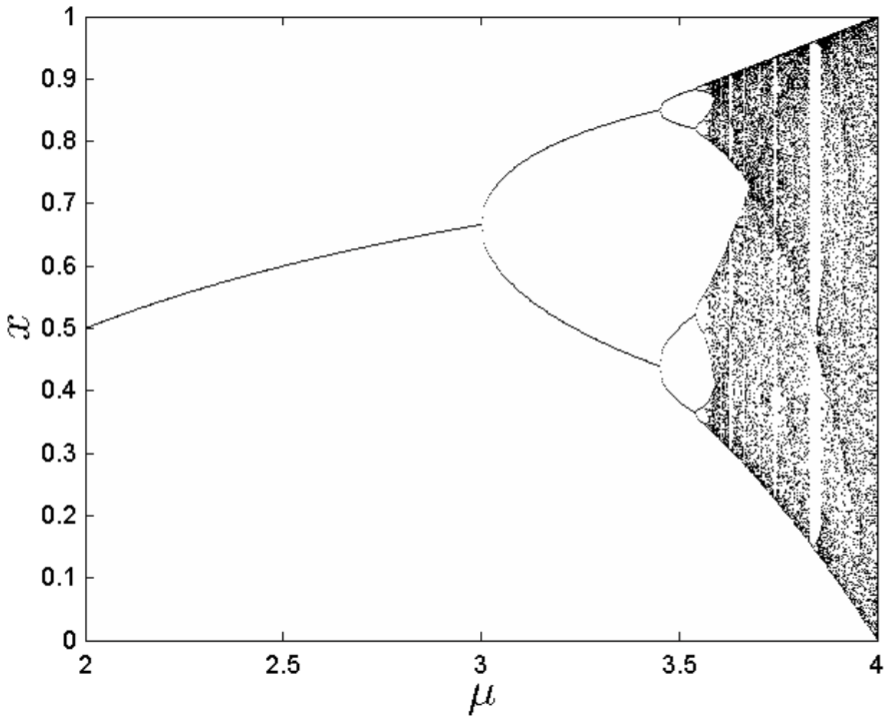
We can compute a bifurcation diagram for the logistic map. For \(2<\mu<4\), we plot the iterates from the map, discarding initial transients. The bifurcation diagram is shown in Fig. 13.10. Notice the uncanny similarity between the bifurcation diagram for the logistic map, and the one we have previously computed for the damped, driven pendulum equation, Fig. \(13.9 .\) Also note that the computation of Fig. 13.10, being on the order of seconds, is substantially faster than that of Fig. 13.9, which took about an hour, because a one-dimensional map is much faster to compute than the Poincaré section of a pair of coupled first-order differential equations.
Computation of the Feigenbaum constant
Period doubling in the logistic map enables an accurate computation of the Feigenbaum constant \(\delta\), defined as
\[\delta=\lim _{n \rightarrow \infty} \delta_{n} \nonumber \]
where
\[\delta_{n}=\frac{\mu_{n+1}-\mu_{n}}{\mu_{n+2}-\mu_{n+1}} \nonumber \]
Table \(13.1\) lists the known first eight values of \(\mu_{n}\) at the bifurcation points. These values, and those at even larger values of \(n\), are in fact very difficult to compute with high precision because of the slow convergence of the iterates at the bifurcation points. Rather, we will instead compute the values of \(\mu\) at what are called superstable cycles. This now well-known method for computing \(\delta\) was first described by Keith Briggs (1989).
Recall that for the general one-dimensional map
\[x_{n+1}=f_{\mu}\left(x_{n}\right), \nonumber \]
a perturbation \(\epsilon_{n}\) to a fixed point \(x_{*}\) decays as
\[\epsilon_{n+1}=f_{\mu}^{\prime}\left(x_{*}\right) \epsilon_{n} . \nonumber \]
At a so-called superstable fixed point, however, \(f_{\mu}^{\prime}\left(x_{*}\right)=0\) and the perturbation decays very much faster as
\[\epsilon_{n+1}=\frac{1}{2} f_{\mu}^{\prime \prime}\left(x_{*}\right) \epsilon_{n}^{2} . \nonumber \]
What are the superstable fixed points of the logistic map? Now, the values \(x_{i}\) that are in the orbit of a period \(-2^{n}\) cycle are fixed points of the composite map
\[x_{n+1}=g_{\mu}\left(x_{n}\right), \nonumber \]
where \(g_{u}=f_{u} \circ f_{u} \circ \cdots \circ f_{u}\), where the composition is repeated \(2^{n}\) times. The orbit of a superstable cycle, then, consists of superstable fixed points of \((13.37)\). If the period- \(2^{n}\) cycle has orbit \(x_{0}, x_{1}, \ldots, x_{2^{n}-1}\), we have \(f_{\mu}\left(x_{0}\right)=x_{1}, f_{\mu}\left(x_{1}\right)=x_{2}, \ldots, f_{\mu}\left(x_{2^{n}-1}\right)=x_{0}\), and by the chain rule,
\[g_{\mu}^{\prime}\left(x_{i}\right)=f_{\mu}^{\prime}\left(x_{0}\right) f_{\mu}^{\prime}\left(x_{1}\right) \cdots f_{\mu}^{\prime}\left(x_{2^{n}-1}\right), \nonumber \]
for all \(x_{i}\) in the orbit of the period- \(2^{n}\) cycle. With
\[f_{\mu}^{\prime}(x)=\mu(1-2 x) \nonumber \]
we have \(g_{\mu}^{\prime}(x)=0\) for \(x=1 / 2\). Therefore, if \(x_{0}=1 / 2\), say, is in the orbit of a period- \(2^{n}\) cycle, then this cycle is superstable. At the bifurcation point creating a period-2 \(^{n}\) cycle, the cycle has marginal stability and \(g_{\mu}^{\prime}\left(x_{0}\right)=1 .\) As \(\mu\) increases, \(g_{\mu}^{\prime}\left(x_{0}\right)\) decreases, and eventually the period-2 \(^{n}\) cycle loses stability when \(g_{\mu}^{\prime}\left(x_{0}\right)=-1\). At some intermediate value of \(\mu\), then, there exists a value of \(x_{0}\) with \(g_{\mu}^{\prime}\left(x_{0}\right)=0\), and here we may assign \(x_{0}=1 / 2 .\) Therefore, every period- \(2^{n}\) cycle contains a value of \(\mu\) for which \(x_{0}=1 / 2\) is in the orbit of the cycle.
Accordingly, we define \(m_{n}\) to be the value of \(\mu\) at which \(x_{0}=1 / 2\) is in the orbit of the period- \(2^{n}\) cycle. We can modify the definition of the Feigenbaum constant (13.33) to be
\[\delta_{n}=\frac{m_{n+1}-m_{n}}{m_{n+2}-m_{n+1}} . \nonumber \]
Though the values of \(\delta_{n}\) computed from (13.33) and (13.40) will differ slightly, the values as \(n \rightarrow \infty\) should be the same.
We can easily determine the first two values of \(m_{n}\). For the period-1 cycle, we have
\[\frac{1}{2}=m_{0} \frac{1}{2}\left(1-\frac{1}{2}\right) \nonumber \]
or \(m_{0}=2\), as confirmed from Fig. 13.10. To determine \(m_{1}\), we make use of the period-2 cycle given by \((13.21)\), and Fig. \((13.10)\), which shows that the smaller root passes through \(x_{0}=1 / 2\). Therefore,
\[\frac{1}{2}=\frac{1}{2 m_{1}}\left(\left(m_{1}+1\right)-\sqrt{\left(m_{1}+1\right)\left(m_{1}-3\right)}\right) ; \nonumber \]
and solving for \(m_{1}\), we obtain the quadratic equation
\[m_{1}^{2}-2 m_{1}-4=0 \nonumber \]
with solution \(m_{1}=1+\sqrt{5} \approx 3.2361\). Further values of \(m_{n}\) will be computed numerically.
To determine \(m_{n}\), we need to solve the equation \(G(\mu)=0\), where
\[G(\mu)=g_{\mu}(1 / 2)-\frac{1}{2} \nonumber \]
and where as before, \(g_{\mu}(x)\) is the composition of \(f_{\mu}(x)\) repeated \(2^{n}\) times. The roots of (13.44) are given by \(m_{0}, m_{1}, \ldots m_{n}\), so that the desired root is the largest one.
We shall use Newton’s method, \(\S 2.2\), to solve (13.44). To implement Newton’s method, we need to compute both \(G(\mu)\) and \(G^{\prime}(\mu)\). Define \(N=2^{n}\). Then using the logistic map
\[x_{n+1}=\mu x_{n}\left(1-x_{n}\right), \nonumber \]
and iterating with \(x_{0}=1 / 2\), we obtain \(x_{1}, x_{2}, \ldots, x_{N} .\) This orbit is superstable if \(x_{N}=1 / 2\). Therefore, we have
\[G(\mu)=x_{N}-1 / 2 \nonumber \]
Moreover,
\[G^{\prime}(\mu)=x_{N^{\prime}}^{\prime} \nonumber \]
where the derivative is with respect to \(\mu\). From (13.45), we have
\[\begin{aligned} x_{n+1}^{\prime} &=x_{n}\left(1-x_{n}\right)+\mu x_{n}^{\prime}\left(1-x_{n}\right)-\mu x_{n} x_{n}^{\prime} \\ &=x_{n}\left(1-x_{n}\right)+\mu x_{n}^{\prime}\left(1-2 x_{n}\right) . \end{aligned} \nonumber \]
Since we always choose \(x_{0}=1 / 2\), independent of \(\mu\), we have as a starting value \(x_{0}^{\prime}=0 .\) Therefore, to compute both \(x_{N}\) and \(x_{N^{\prime}}^{\prime}\) we iterate \(2^{n}\) times the coupled map equations
\[\begin{aligned} &x_{n+1}=\mu x_{n}\left(1-x_{n}\right) \\ &x_{n+1}^{\prime}=x_{n}\left(1-x_{n}\right)+\mu x_{n}^{\prime}\left(1-2 x_{n}\right) \end{aligned} \nonumber \]
| \(n\) | \(m_{n}\) | \(\delta_{n}\) |
|---|---|---|
| 0 | 2 | \(4.7089430135405\) |
| 1 | \(1+\sqrt{5}\) | \(4.6807709980107\) |
| 2 | \(3.4985616993277\) | \(4.6629596111141\) |
| 3 | \(3.5546408627688\) | \(4.6684039259164\) |
| 4 | \(3.5666673798563\) | \(4.6689537409802\) |
| 5 | \(3.5692435316371\) | \(4.6691571813703\) |
| 6 | \(3.5697952937499\) | \(4.6691910014915\) |
| 7 | \(3.5699134654223\) | \(4.6691994819801\) |
| 8 | \(3.5699387742333\) | \(4.6692010884670\) |
| 9 | \(3.5699441946081\) | \(4.6692015881423\) |
| 10 | \(3.5699453554865\) | \(4.6692023902759\) |
| 11 | \(3.5699456041111\) | \(4.6691974782669\) |
| 12 | \(3.5699456573588\) | \(4.6693329633696\) |
| 13 | \(3.5699456687629\) | |
| 14 | \(3.5699456712052\) |
Table 13.2: The first fourteen values of \(m_{n}\), and estimates of the Feigenbaum delta.
with initial values \(x_{0}=1 / 2\) and \(x_{0}^{\prime}=0 .\) Newton’s method then solves for \(m_{n}\) by iterating
\[\mu^{(i+1)}=\mu^{(i)}-\frac{x_{N}-1 / 2}{x_{N}^{\prime}}, \nonumber \]
until convergence of \(\mu^{(i)}\) to \(m_{n}\). In double precision, we have been able to achieve a precision of about 14 digits, which we find can be obtained in fewer than 5 iterations of Newton’s method.
For Newton’s method to converge to \(m_{n}\), we need a good guess for \(\mu^{(0)} .\) We can use the previous best estimate for the Feigenbaum delta to predict \(m_{n}\). From \((13.40)\), we find
\[\mu^{(0)}=m_{n-1}+\frac{m_{n-1}-m_{n-2}}{\delta_{n-2}} . \nonumber \]
Although we can not compute \(\delta_{n-2}\) without knowing \(m_{n}\), we can nevertheless use the estimate \(\delta_{n-2} \approx \delta_{n-3} .\) The computation, then, starts with \(n=2\), and we can begin by taking \(\delta_{-1}=4.4\), so that, for example,
\[\begin{aligned} \mu^{(0)} &=3.2361+\frac{3.2361-2}{4.4} \\ &=3.5170 . \end{aligned} \nonumber \]
Using this algorithm, we have produced Table \(13.2\) for \(m_{n}\), with corresponding calculations of \(\delta_{n} .\) As the values of \(m_{n}\) converge, the corresponding values of \(\delta_{n}\) begin to lose precision. It would appear that our best estimate from the table is \(\delta \approx 4.66920\), compared to the known value of \(\delta=4.669201609102990 \ldots\), computed by a different algorithm capable of achieving higher precision.
Strange attractor of the chaotic pendulum
After the period-doubling cascade, the pendulum motion becomes chaotic. We choose parameter values \(q=4, f=1.5\), and \(\omega=2 / 3\) in the chaotic regime, and after discarding an initial transient of 256 forcing periods, compute a Poincaré section of the phase-space trajectory in the \(\theta-\dot{\theta}\) plane, sampling points every forcing period. The values of the periodic variable \(\theta\) are mapped onto the interval \(-\pi<\theta<\pi\). The full Poincaré section consisting of 50,000 points is shown in the top drawing of Fig. 13.11, and a blowup of the points within the drawn rectangle (from a sample of 200,000 points over the entire attractor) is shown in the bottom drawing.
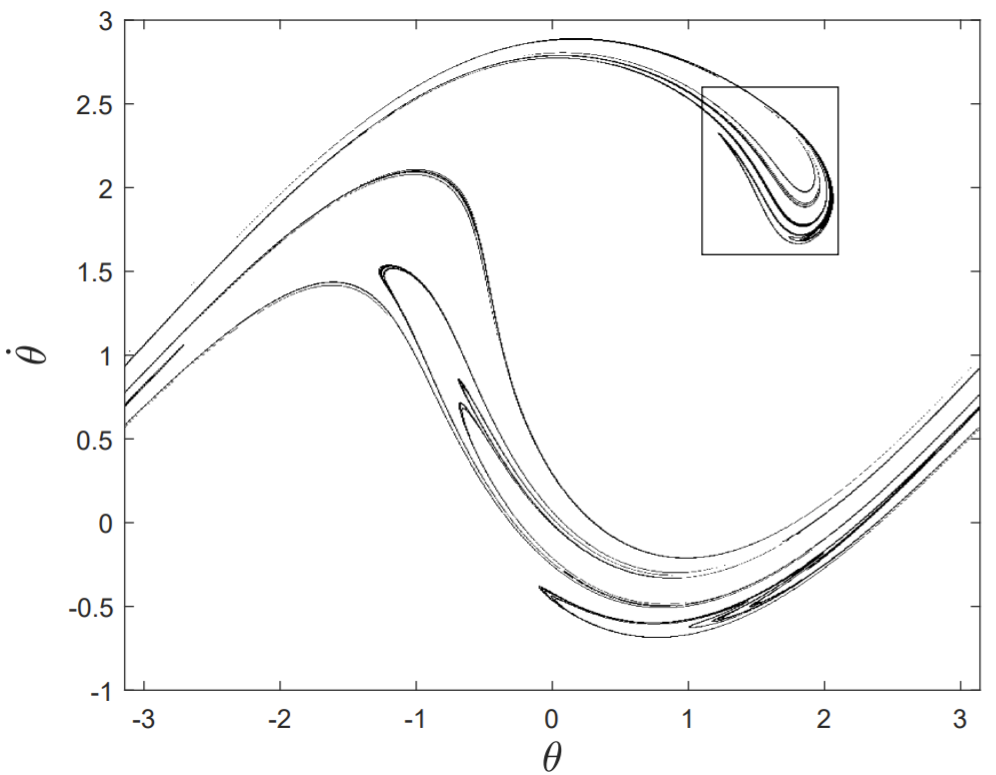
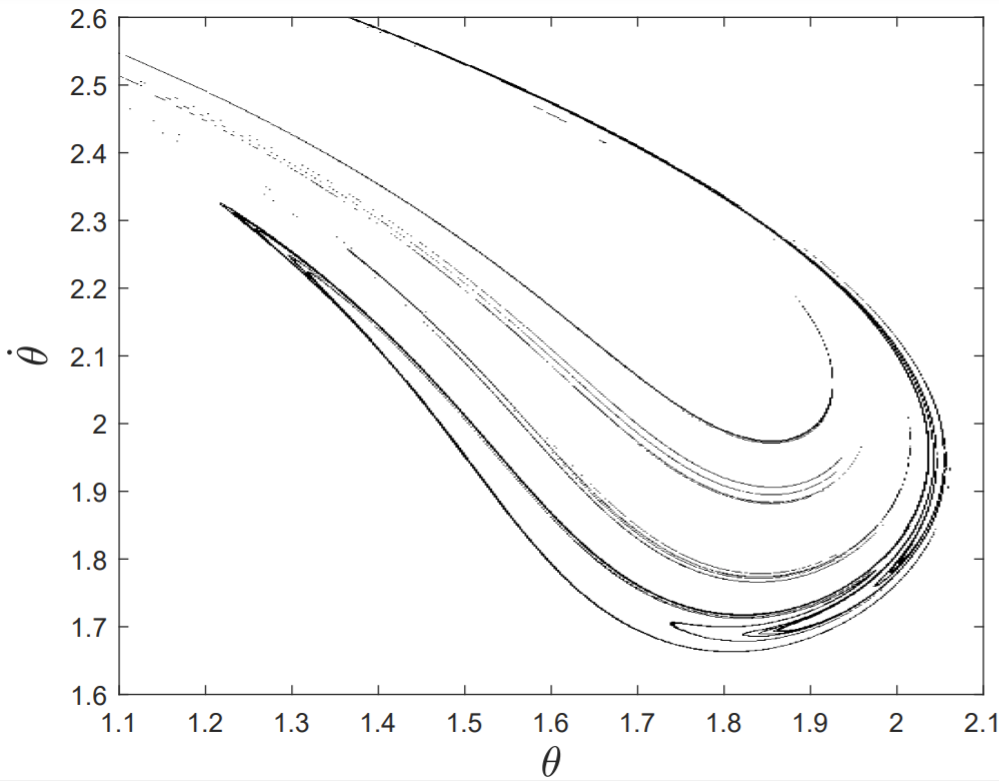
From Fig. 13.11, it appears that the Poincaré section has structure on all scales, which is reminiscent of the classical fractals discussed in \(\S 12.7\). The set of points shown in Fig. 13.11 is called a strange attractor, and will be seen to have a fractional correlation dimension.
Using the algorithm for computing a correlation dimension discussed in \(\S 12.7\), we draw a
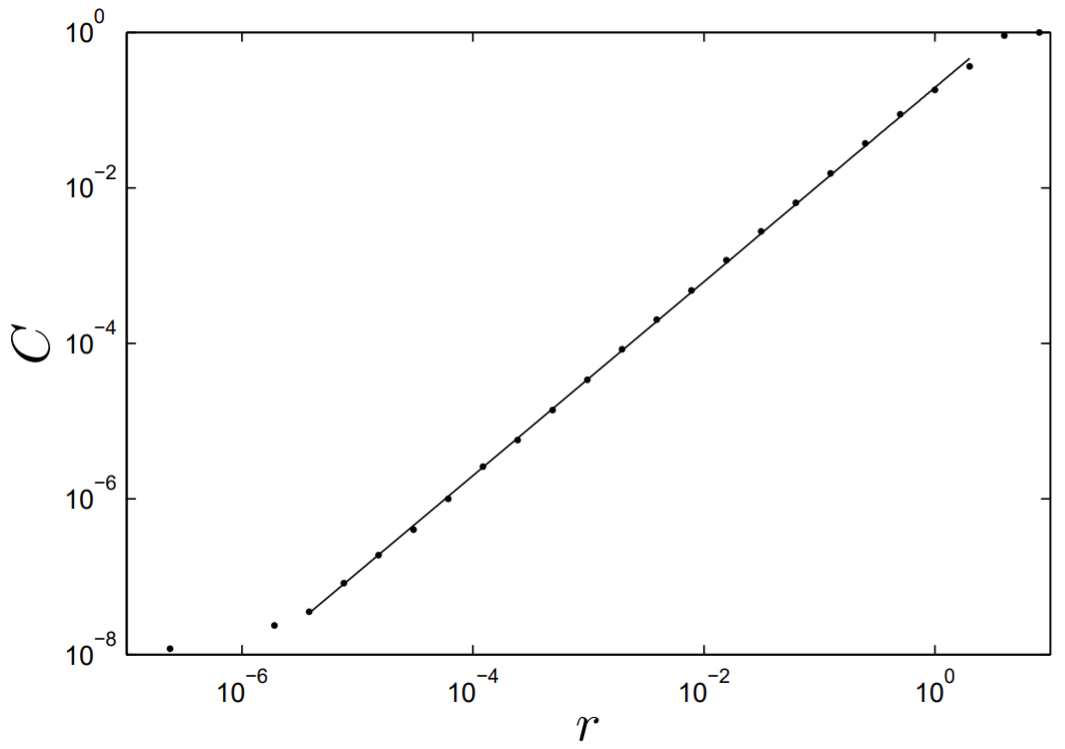
log-log plot of the correlation integral \(C(r)\) versus \(r\), shown in Fig. 13.12. A least-squares fit of a straight line to the middle region of the plot yields a correlation dimension for the Poincaré section of approximately \(D=1.25\).