Skip to main content
Mathematics LibreTexts

3.3: The Fundamental Dichotomy for Julia sets

  1. Last updated
  2. Save as PDF
  • Page ID
    101395

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Disconnected Julia sets

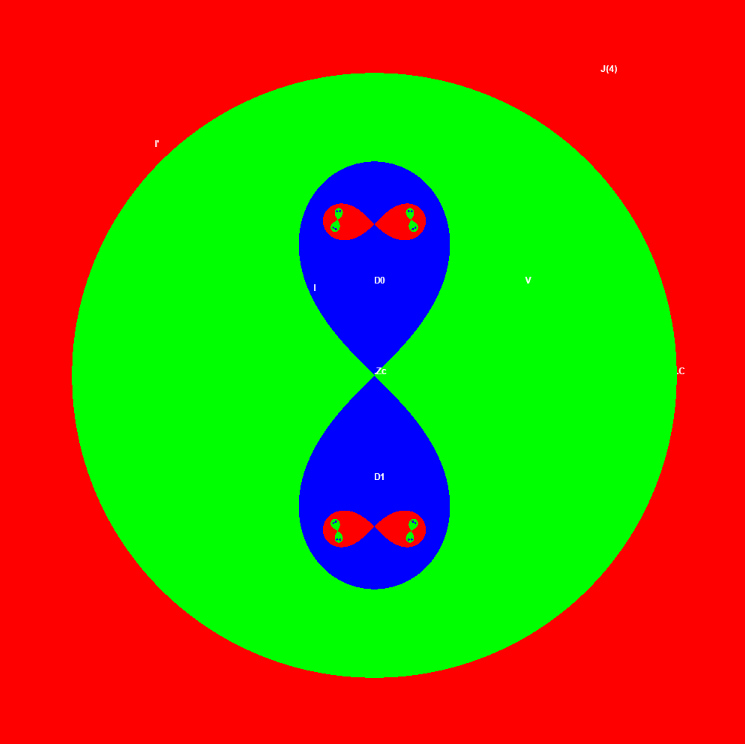
    3.3.1.png
    Figure \(\PageIndex{1}\)

    Let orbit of the critical point zc = 0 (and therefore the z = f(0) = c point) goes to infinity. Consider the Julia set J(4) as an example. We take a circle l', which goes through z = c = 4 . Each point of l' has two preimages ±(z - c)½ with the exeption of z = c, which has the only preimage zc. Therefore preimage of l' is the figure eight curve l. The two disks D0 , D1 are mapped by fc in one-to-one fashion onto the V disk (it contains both D0 , D1). The Julia set J(4) is contained inside D0 ∪ D1 and is divided by the l curve in two disconnected parts. As you can see in these pictures, one can proceed this process ad infinitum therefore the Julia set J(4) has infinitely many components.

    3.3.2.png
    Figure \(\PageIndex{2}\)

    Connected Julia sets

    3.3.3.png
    Figure \(\PageIndex{3}\)
     

    If the critical orbit does not escape to infinity, then J(c) is a connected set. You can see to the left, that f -1 maps l' curve into l one. l' never contains z = c value, therefore each point of l' has two different preimages ±(z - c)½ and l can not be a figure eight curve. In a similar way any closed curve outside the Julia set never is a figure eight curve and can not break the Julia set.

    The Fundamental Dichotomy

    1. If fcn(0)→∞ , the filled Julia set of fc is a Cantor set.
    2. Otherwise, the filled Julia set of fc is a connected set.

    This page titled 3.3: The Fundamental Dichotomy for Julia sets is shared under a Public Domain license and was authored, remixed, and/or curated by via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.