1.8: Surfaces
- Page ID
- 601
Cylinders
Let C be a curve, then we define a cylinder to be the set of all lines through C and perpendicular to the plane that C lies in.
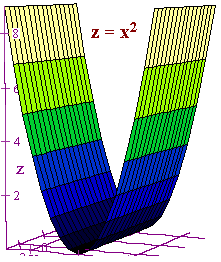
We can tell that an equation is a cylinder is it is missing one of the variables.
Quadric Surfaces
Recall that the quadrics or conics are lines , hyperbolas, parabolas, circles, and ellipses. In three dimensions, we can combine any two of these and make a quadric surface. For example
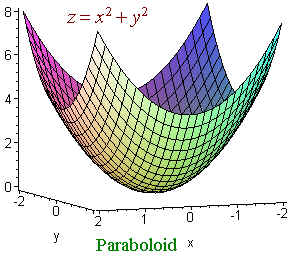
is a paraboloid since for constant z we get a circle and for constant x or y we get a parabola. We use the suffix -oid to mean ellipse or circle. We have:
\[\begin{align} \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2 } + \dfrac{z^2}{c^2} &=1 \;\;\; \text{is an ellipsoid,} \\ -\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2 } + \dfrac{z^2}{c^2} &=1 \;\;\; \text{is a hyperboloid of 2 sheets, while} \\ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2 } - \dfrac{z^2}{c^2} &=1 \;\;\; \text{is a hyperboloid of 1 sheet.} \end{align}\nonumber \]
Surface of Revolution
Let \(y = f(x)\) be a curve, then the equation of the surface of revolution abut the x-axis is
\[ y^2 + z^2 = f^2(x). \nonumber \]
Example \(\PageIndex{1}\)
Find the equation of the surface that is formed when the curve
\[ y = \sin x\nonumber \]
with
\[ 0 \le x < \dfrac{\pi}{2} \nonumber \]
is revolved around the y-axis.
Solution
This uses a different formula since this time the curve is revolved around the y-axis.
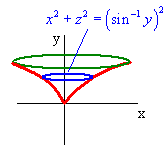
The circular cross section has radius \(\sin^{-1}y\) and the circle is perpendicular to the y-axis. Hence the equation is
\[ x^2 + z^2 = (\sin^{-1} y)^2. \nonumber \]
Cylindrical Coordinates
We can extend polar coordinates to three dimensions by
\[ x = r\, \cos\, q, \nonumber \]
\[ y = r\, \sin\, q,\nonumber \]
\[ z = z.\nonumber \]
Example \(\PageIndex{2}\)
We can write \((1,1,3)\) in cylindrical coordinates. We find
\[ r = \sqrt{1^2 + 1^2} = sqrt{2} \nonumber \]
and
\[ \theta = \tan^{-1} \left(\dfrac{1}{1} \right) = \dfrac{\pi}{4} \nonumber \]
so that the cylindrical coordinates are
\[ ( \sqrt{2}, \frac{\pi}{4},3).\nonumber \]
Spherical Coordinates
An alternate coordinate system works on a distance and two angle method called spherical coordinates. We let \(r\) denote the distance from the point to the origin, \(\theta\) represent the same \(\theta\) as in cylindrical coordinates, and \(\phi\) denote the angle from the positive z-axis to the point.
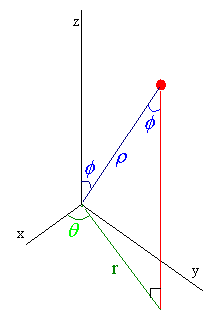
The picture tells us that
\[ r = r \sin \phi\nonumber \]
and that
\[ z = r \cos \phi .\nonumber \]
From this we can find
- \(x = r\cos \theta = r \sin \phi \cos \theta \),
- \(y = r \sin \theta = r \sin \phi \sin \theta \),
- \(z = r \cos \phi \).
Immediately we see that
\[ x^2 + y^2 + z^2 = r^2. \nonumber \]
We use spherical coordinates whenever the problem involves a distance from a source.
Example \(\PageIndex{3}\)
Convert the surface
\[ z = x^2 + y^2 \nonumber \]
to an equation in spherical coordinates.
Solution
We add \(z^2\) to both sides
\[ z + z^2 = x^2 + y^2 + z^2. \nonumber \]
Now it is easier to convert
\[ r\, \cos \phi + r^2 \, \cos^2 \phi = r^2. \nonumber \]
Divide by \(r\) to get
\[ \cos \phi + r\, \cos^2 \phi = r .\nonumber \]
Now solve for \(r\).
\[ r = \dfrac{\cos \phi }{1 - \cos^2 \phi } = \dfrac{\cos \phi }{\sin^2 \phi } = \csc \phi \; \cot \phi .\nonumber \]
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


