5.5: Definite Integral Intro Exercises

T

5.2: The Definite Integral

In the following exercises, express the limits as integrals.

60) \(\displaystyle \lim_{n→∞}\sum_{i=1}^n(x^∗_i)Δx\) over \(\displaystyle [1,3]\)

61) \(\displaystyle \lim_{n→∞}\sum_{i=1}^n(5(x^∗_i)^2−3(x^∗_i)^3)Δx\) over \(\displaystyle [0,2]\)

Answer:

\(\displaystyle ∫^2_0(5x^2−3x^3)dx\)

62) \(\displaystyle \lim_{n→∞}\sum_{i=1}^nsin^2(2πx^∗_i)Δx\) over \(\displaystyle [0,1]\)

63) \(\displaystyle \lim_{n→∞}\sum_{i=1}^ncos^2(2πx^∗_i)Δx\) over \(\displaystyle [0,1]\)

Answer:

\(\displaystyle ∫^1_0cos^2(2πx)dx\)

In the following exercises, given \(\displaystyle L_n\) or \(\displaystyle R_n\) as indicated, express their limits as \(\displaystyle n→∞\) as definite integrals, identifying the correct intervals.

64) \(\displaystyle L_n=\frac{1}{n}\sum_{i=1}^n\frac{i−1}{n}\)

65) \(\displaystyle R_n=\frac{1}{n}\sum_{i=1}^n\frac{i}{n}\)

Answer:

\(\displaystyle f_{ave}= \frac{45}{28}\)

Solution: \(\displaystyle ∫^1_0xdx\)

66) \(\displaystyle Ln=\frac{2}{n}\sum_{i=1}^n(1+2\frac{i−1}{n})\)

67) \(\displaystyle R_n=\frac{3}{n}\sum_{i=1}^n(3+3\frac{i}{n})\)

Solution: \(\displaystyle ∫^6_3xdx\)

68) \(\displaystyle L_n=\frac{2π}{n}\sum_{i=1}^n2π\frac{i−1}{n}cos(2π\frac{i−1}{n})\)

69 \(\displaystyle R_n=\frac{1}{n}\sum_{i=1}^n(1+\frac{i}{n})log((1+\frac{i}{n})^2)\)

Solution: \(\displaystyle ∫^2_1xlog(x^2)dx\)

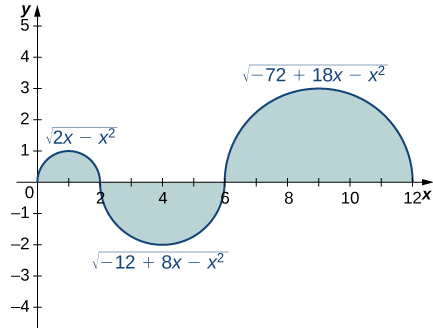
In the following exercises, evaluate the integrals of the functions graphed using the formulas for areas of triangles and circles, and subtracting the areas below the x-axis.

70)

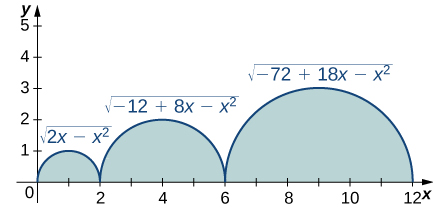
71)

Solution: \(\displaystyle 1+2⋅2+3⋅3=14\)

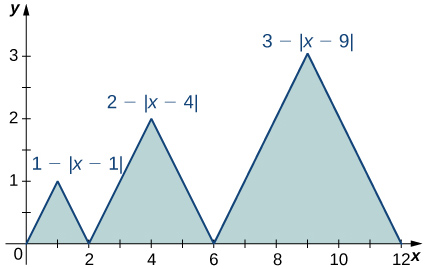
72)

73)

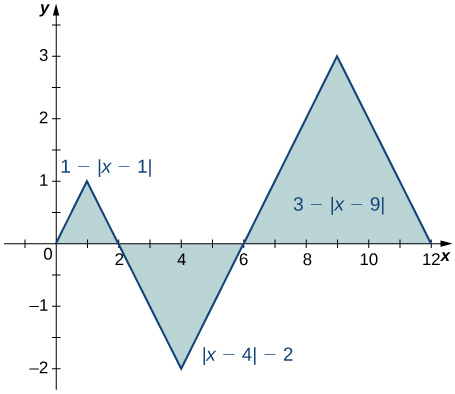
Solution: \(\displaystyle 1−4+9=6\)

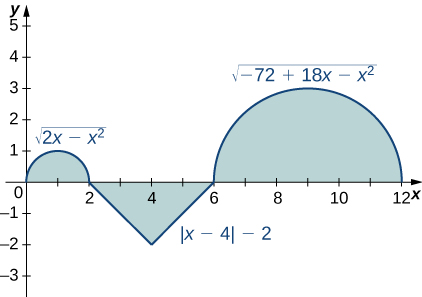
74)

75)

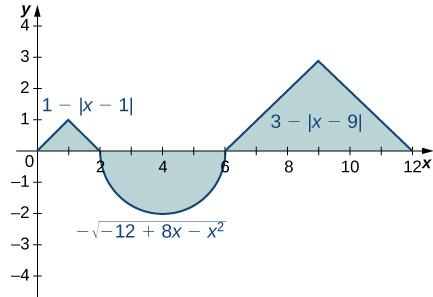
Solution: \(\displaystyle 1−2π+9=10−2π\)

In the following exercises, evaluate the integral using area formulas.

76) \(\displaystyle ∫^3_0(3−x)dx\)

77) \(\displaystyle ∫^3_2(3−x)dx\)

Answer:

The integral is the area of the triangle, \(\displaystyle \dfrac{1}{2}\)

78) \(\displaystyle ∫^3_{−3}(3−|x|)dx\)

79) \(\displaystyle ∫^6_0(3−|x−3|)dx\)

Solution: The integral is the area of the triangle, \(\displaystyle 9.\)

80) \(\displaystyle ∫^2_{−2}\sqrt{4−x^2}dx\)

81) \(\displaystyle ∫^5_1\sqrt{4−(x−3)^2}dx\)

Soluti0n: The integral is the area \(\displaystyle \frac{1}{2}πr^2=2π.\)

82) \(\displaystyle ∫^{12}_0\sqrt{36−(x−6)^2}dx\)

83) \(\displaystyle ∫^3_{−2}(3−|x|)dx\)

Solution: The integral is the area of the “big” triangle less the “missing” triangle, \(\displaystyle 9−\frac{1}{2}.\)

In the following exercises, use averages of values at the left (L) and right (R) endpoints to compute the integrals of the piecewise linear functions with graphs that pass through the given list of points over the indicated intervals.

84) \(\displaystyle {(0,0),(2,1),(4,3),(5,0),(6,0),(8,3)}\) over \(\displaystyle [0,8]\)

85) \(\displaystyle {(0,2),(1,0),(3,5),(5,5),(6,2),(8,0)}\) over \(\displaystyle [0,8]\)

Solution: \(\displaystyle L=2+0+10+5+4=21,R=0+10+10+2+0=22,\dfrac{L+R}{2}=21.5\)

86) \(\displaystyle {(−4,−4),(−2,0),(0,−2),(3,3),(4,3)}\) over \(\displaystyle [−4,4]\)

87) \(\displaystyle {(−4,0),(−2,2),(0,0),(1,2),(3,2),(4,0)}\) over \(\displaystyle [−4,4]\)

Solution: \(\displaystyle L=0+4+0+4+2=10,R=4+0+2+4+0=10,\dfrac{L+R}{2}=10\)

Suppose that \(\displaystyle ∫^4_0f(x)dx=5\) and \(\displaystyle ∫^2_0f(x)dx=−3\), and \(\displaystyle ∫^4_0g(x)dx=−1\) and \(\displaystyle ∫^2_0g(x)dx=2\). In the following exercises, compute the integrals.

88) \(\displaystyle ∫^4_0(f(x)+g(x))dx\)

89) \(\displaystyle ∫^4_2(f(x)+g(x))dx\)

Answer:

\(\displaystyle ∫^4_2f(x)dx+∫^4_2g(x)dx=8−3=5\)

90) \(\displaystyle ∫^2_0(f(x)−g(x))dx\)

91) \(\displaystyle ∫^4_2(f(x)−g(x))dx\)

Answer:

\(\displaystyle ∫^4_2f(x)dx−∫^4_2g(x)dx=8+3=11\)

92) \(\displaystyle ∫^2_0(3f(x)−4g(x))dx\)

93) \(\displaystyle ∫^4_2(4f(x)−3g(x))dx\)

Answer:

\(\displaystyle 4∫^4_2f(x)dx−3∫^4_2g(x)dx=32+9=41\)

In the following exercises, use the identity \(\displaystyle ∫^A_{−A}f(x)dx=∫^0_{−A}f(x)dx+∫^A_0f(x)dx\) to compute the integrals.

94) \(\displaystyle ∫^π_{−π}\frac{sint}{1+t^2}dt\) (Hint: \(\displaystyle sin(−t)=−sin(t))\)

95) \(\displaystyle ∫^{\sqrt{π}}_\sqrt{−π}\frac{t}{1+cost}dt\)

Solution: The integrand is odd; the integral is zero.

96) \(\displaystyle ∫^3_1(2−x)dx\) (Hint: Look at the graph of f.)

97) \(\displaystyle ∫^4_2(x−3)^3dx\) (Hint: Look at the graph of f.)

Solution: The integrand is antisymmetric with respect to \(\displaystyle x=3.\) The integral is zero.

In the following exercises, given that \(\displaystyle ∫^1_0xdx=\frac{1}{2},∫^1_0x^2dx=\frac{1}{3},\) and \(\displaystyle ∫^1_0x^3dx=\frac{1}{4}\), compute the integrals.

98) \(\displaystyle ∫^1_0(1+x+x^2+x^3)dx\)

99) \(\displaystyle ∫^1_0(1−x+x^2−x^3)dx\)

Answer:

\(\displaystyle 1−\frac{1}{2}+\frac{1}{3}−\frac{1}{4}=\frac{7}{12}\)

100) \(\displaystyle ∫^1_0(1−x)^2dx\)

101) \(\displaystyle ∫^1_0(1−2x)^3dx\)

Solution: \(\displaystyle ∫^1_0(1−2x+4x^2−8x^3)dx=1−1+\frac{4}{3}−2=−\frac{2}{3}\)

102) \(\displaystyle ∫^1_0(6x−\frac{4}{3}x^2)dx\)

103) \(\displaystyle ∫^1_0(7−5x^3)dx\)

Solution: \(\displaystyle 7−\frac{5}{4}=\frac{23}{4}\)

In the following exercises, use the comparison theorem.

104) Show that \(\displaystyle ∫^3_0(x^2−6x+9)dx≥0.\)

105) Show that \(\displaystyle ∫^3_{−2}(x−3)(x+2)dx≤0.\)

Solution: The integrand is negative over \(\displaystyle [−2,3].\)

106) Show that \(\displaystyle ∫^1_0\sqrt{1+x^3}dx≤∫^1_0\sqrt{1+x^2}dx\).

107) Show that \(\displaystyle ∫^2_1\sqrt{1+x}dx≤∫^2_1\sqrt{1+x^2}dx.\)

Solution: \(\displaystyle x≤x^2\) over \(\displaystyle [1,2]\), so \(\displaystyle \sqrt{1+x}≤\sqrt{1+x^2}\) over \(\displaystyle [1,2].\)

108) Show that \(\displaystyle ∫^{π/2}_0sintdt≥\frac{π}{4})\) (Hint: \(\displaystyle sint≥\frac{2t}{π}\) over \(\displaystyle [0,\frac{π}{2}])\)

109) Show that \(\displaystyle ∫^{π/4}_{−π/4}costdt≥π\sqrt{2}/4\).

Solution: \(\displaystyle cos(t)≥\dfrac{\sqrt{2}}{2}\). Multiply by the length of the interval to get the inequality.

In the following exercises, approximate the average value using Riemann sums \(\displaystyle L_{100}\) and \(\displaystyle R_{100}\). How does your answer compare with the exact given answer?

116) [T] \(\displaystyle y=ln(x)\) over the interval \(\displaystyle [1,4]\); the exact solution is \(\displaystyle \frac{ln(256)}{3}−1.\)

117) [T] \(\displaystyle y=e^{x/2}\) over the interval \(\displaystyle [0,1]\); the exact solution is \(\displaystyle 2(\sqrt{e}−1).\)

5olution: \(\displaystyle L_{100}=1.294,R_{100}=1.301;\) the exact average is between these values.

118) [T] \(\displaystyle y=tanx\) over the interval \(\displaystyle [0,\frac{π}{4}]\); the exact solution is \(\displaystyle \frac{2ln(2)}{π}\).

119) [T] \(\displaystyle y=\frac{x+1}{\sqrt{4−x^2}}\) over the interval \(\displaystyle [−1,1]\); the exact solution is \(\displaystyle \frac{π}{6}\).

Solution: \(\displaystyle L_{100}×(\frac{1}{2})=0.5178,R_{100}×(\frac{1}{2})=0.5294\)

In the following exercises, compute the average value using the left Riemann sums \(\displaystyle L_N\) for \(\displaystyle N=1,10,100\). How does the accuracy compare with the given exact value?

120) [T] \(\displaystyle y=x^2−4\) over the interval \(\displaystyle [0,2]\); the exact solution is \(\displaystyle −\frac{8}{3}\).

121) [T] \(\displaystyle y=xe^{x^2}\) over the interval \(\displaystyle [0,2]\); the exact solution is \(\displaystyle \frac{1}{4}(e^4−1).\)

Solution: \(\displaystyle L_1=0,L_{10}×(\frac{1}{2})=8.743493,L_{100}×(\frac{1}{2})=12.861728.\) The exact answer \(\displaystyle ≈26.799,\) so \(\displaystyle L_{100}\) is not accurate.

122) [T] \(\displaystyle y=(\frac{1}{2})^x\) over the interval \(\displaystyle [0,4]\); the exact solution is \(\displaystyle \frac{15}{64ln(2)}\).

123) [T] \(\displaystyle y=xsin(x^2)\) over the interval \(\displaystyle [−π,0]\); the exact solution is \(\displaystyle \frac{cos(π^2)−1}{2π.}\)

Solution: \(\displaystyle L_1×(\frac{1}{π})=1.352,L_{10}×(\frac{1}{π})=−0.1837,L_{100}×(1π)=−0.2956.\) The exact answer \(\displaystyle ≈−0.303,\) so \(\displaystyle L_{100}\) is not accurate to first decimal.

124) Suppose that \(\displaystyle A=∫^{2π}_0sin^2tdt\) and \(\displaystyle B=∫^{2π}_0cos^2tdt.\) Show that \(\displaystyle A+B=2π\) and \(\displaystyle A=B.\)

125) Suppose that \(\displaystyle A=∫^{π/4}_{−π/4}sec^2tdt=π\) and \(\displaystyle B=∫^{π/4}_{−π/}4tan^2tdt.\) Show that \(\displaystyle A−B=\frac{π}{2}\).

Solution: Use \(\displaystyle tan^2θ+1=sec^2θ.\) Then, \(\displaystyle B−A=∫^{π/4}_{−π/4}1dx=\frac{π}{2}.\)

126) Show that the average value of \(\displaystyle sin^2t\) over \(\displaystyle [0,2π]\) is equal to \(\displaystyle 1/2\) Without further calculation, determine whether the average value of \(\displaystyle sin^2t\) over \(\displaystyle [0,π]\) is also equal to \(\displaystyle 1/2.\)

127) Show that the average value of \(\displaystyle cos^2t\) over \(\displaystyle [0,2π]\) is equal to \(\displaystyle 1/2\). Without further calculation, determine whether the average value of \(\displaystyle cos^2(t)\) over \(\displaystyle [0,π]\) is also equal to \(\displaystyle 1/2.\)

Solution: \(\displaystyle ∫^{2π}_0cos^2tdt=π,\) so divide by the length 2π of the interval. \(\displaystyle cos^2t\) has period π, so yes, it is true.

128) Explain why the graphs of a quadratic function (parabola) \(\displaystyle p(x)\) and a linear function ℓ(x) can intersect in at most two points. Suppose that \(\displaystyle p(a)=ℓ(a)\) and \(\displaystyle p(b)=ℓ(b)\), and that \(\displaystyle ∫^b_ap(t)dt>∫^b_aℓ(t)dt\). Explain why \(\displaystyle ∫^d_cp(t)>∫^d_cℓ(t)dt\) whenever \(\displaystyle a≤c<d≤b.\)

129) Suppose that parabola \(\displaystyle p(x)=ax^2+bx+c\) opens downward \(\displaystyle (a<0)\) and has a vertex of \(\displaystyle y=\frac{−b}{2a}>0\). For which interval \(\displaystyle [A,B]\) is \(\displaystyle ∫^B_A(ax^2+bx+c)dx\) as large as possible?

Solution: The integral is maximized when one uses the largest interval on which p is nonnegative. Thus, \(\displaystyle A=\frac{−b−\sqrt{b^2−4ac}}{2a}\) and \(\displaystyle B=\frac{−b+\sqrt{b^2−4ac}}{2a}.\)

130) Suppose \(\displaystyle [a,b]\) can be subdivided into subintervals \(\displaystyle a=a_0<a_1<a_2<⋯<a_N=b\) such that either \(\displaystyle f≥0\) over \(\displaystyle [a_{i−1},a_i]\) or \(\displaystyle f≤0\) over \(\displaystyle [a_{i−1},a_i]\). Set \(\displaystyle A_i=∫^{a_i}_{a_{i−1}}f(t)dt.\)

a. Explain why \(\displaystyle ∫^b_af(t)dt=A_1+A_2+⋯+A_N.\)

b. Then, explain why \(\displaystyle ∫^b_af(t)dt∣∣∣≤∫^b_a|f(t)|dt.\)

131) Suppose \(\displaystyle f\) and \(\displaystyle g\) are continuous functions such that \(\displaystyle ∫^d_cf(t)dt≤∫^d_cg(t)dt\) for every subinterval \(\displaystyle [c,d]\) of \(\displaystyle [a,b]\). Explain why \(\displaystyle f(x)≤g(x)\) for all values of x.

Solution: If \(\displaystyle f(t_0)>g(t_0)\) for some \(\displaystyle t_0∈[a,b]\), then since \(\displaystyle f−g\) is continuous, there is an interval containing \(\displaystyle t_0\) such that \(\displaystyle f(t)>g(t)\) over the interval \(\displaystyle [c,d]\), and then \(\displaystyle ∫^d_df(t)dt>∫^d_cg(t)d\)over this interval.

132) Suppose the average value of \(\displaystyle f\) over \(\displaystyle [a,b]\) is 1 and the average value of f over [b,c] is 1 where \(\displaystyle a<c<b\). Show that the average value of \(\displaystyle f\) over \(\displaystyle [a,c]\) is also 1.

133) Suppose that \(\displaystyle [a,b]\) can be partitioned. taking \(\displaystyle a=a_0<a_1<⋯<a_N=b\) such that the average value of \(\displaystyle f\) over each subinterval \(\displaystyle [a_{i−1},a_i]=1\) is equal to 1 for each \(\displaystyle i=1,…,N\). Explain why the average value of f over \(\displaystyle [a,b]\) is also equal to 1.

Solution: The integral of f over an interval is the same as the integral of the average of f over that interval. Thus, \(\displaystyle ∫^b_af(t)dt=∫^{a_1}_{a_0}f(t)dt+∫^{a_2}_a{1_f}(t)dt+⋯+∫^{a_N}_{a_{N+1}}f(t)dt=∫^{a_1}_{a_0}1dt+∫^{a_2}_{a_1}1dt+⋯+∫^{a_N}_{a_{N+1}}1dt\)

\(\displaystyle =(a_1−a_0)+(a_2−a_1)+⋯+(a_N−a_{N−1})=a_N−a_0=b−a\).

Dividing through by \(\displaystyle b−a\) gives the desired identity.

134) Suppose that for each i such that \(\displaystyle 1≤i≤N\) one has \(\displaystyle ∫^i_{i−1}f(t)dt=i\). Show that \(\displaystyle ∫^N_0f(t)dt=\frac{N(N+1)}{2}.\)

135) Suppose that for each i such that \(\displaystyle 1≤i≤N\) one has \(\displaystyle ∫^i_{i−1}f(t)dt=i^2\). Show that \(\displaystyle ∫^N_0f(t)dt=\frac{N(N+1)(2N+1)}{6}\).

Solution: \(\displaystyle ∫^N_0f(t)dt=\sum_{i=1}^N∫^i_{i−1}f(t)dt=\sum_{i=1}^Ni^2=\frac{N(N+1)(2N+1)}{6}\)

136) [T] Compute the left and right Riemann sums \(\displaystyle L_{10}\) and \(\displaystyle R_{10}\) and their average \(\displaystyle \frac{L_{10}+R_{10}}{2}\) for \(\displaystyle f(t)=t^2\)over \(\displaystyle [0,1]\). Given that \(\displaystyle ∫^1_0t^2dt=1/3\), to how many decimal places is \(\displaystyle \frac{L_{10}+R_{10}}{2}\) accurate?

137) [T] Compute the left and right Riemann sums, \(\displaystyle L_10\) and \(\displaystyle R_{10}\), and their average \(\displaystyle \frac{L_{10}+R_{10}}{2}\) for \(\displaystyle f(t)=(4−t^2)\) over \(\displaystyle [1,2]\). Given that \(\displaystyle ∫^2_1(4−t^2)dt=1.66\), to how many decimal places is \(\displaystyle \frac{L_{10}+R_{10}}{2}\) accurate?

Solution: \(\displaystyle L_{10}=1.815,R_{10}=1.515,\frac{L_{10}+R_{10}}{2}=1.665,\) so the estimate is accurate to two decimal places.

138) If \(\displaystyle ∫^5_1\sqrt{1+t^4}dt=41.7133...,\) what is \(\displaystyle ∫^5_1\sqrt{1+u^4}du?\)

139) Estimate \(\displaystyle ∫^1_0tdt\) using the left and right endpoint sums, each with a single rectangle. How does the average of these left and right endpoint sums compare with the actual value \(\displaystyle ∫^1_0tdt?\)

Solution: The average is \(\displaystyle 1/2,\) which is equal to the integral in this case.

140) Estimate \(\displaystyle ∫^1_0tdt\) by comparison with the area of a single rectangle with height equal to the value of t at the midpoint \(\displaystyle t=\frac{1}{2}\). How does this midpoint estimate compare with the actual value \(\displaystyle ∫^1_0tdt?\)

141) From the graph of \(\displaystyle sin(2πx)\) shown:

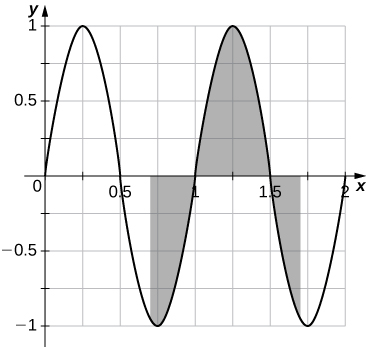
a. Explain why \(\displaystyle ∫^1_0sin(2πt)dt=0.\)

b. Explain why, in general, \(\displaystyle ∫^{a+1}_asin(2πt)dt=0\) for any value of a.

Answer:

a. The graph is antisymmetric with respect to \(\displaystyle t=\frac{1}{2}\) over \(\displaystyle [0,1]\), so the average value is zero.
b. For any value of a, the graph between \(\displaystyle [a,a+1]\) is a shift of the graph over \(\displaystyle [0,1]\), so the net areas above and below the axis do not change and the average remains zero.

142) If f is 1-periodic \(\displaystyle (f(t+1)=f(t))\), odd, and integrable over \(\displaystyle [0,1]\), is it always true that \(\displaystyle ∫^1_0f(t)dt=0?\)

143) If f is 1-periodic and \(\displaystyle ∫10f(t)dt=A,\) is it necessarily true that \(\displaystyle ∫^{1+a}_af(t)dt=A\) for all A?

Solution: Yes, the integral over any interval of length 1 is the same.

J5.2.1) not here yet