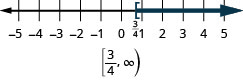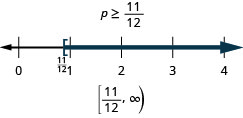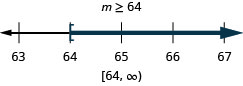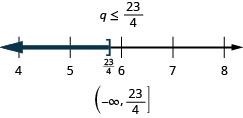2.6: Solve Linear Inequalities

Last updated
Save as PDF

Page ID: 33038

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

By the end of this section, you will be able to:

Graph inequalities on the number line
Solve linear inequalities
Translate words to an inequality and solve
Solve applications with linear inequalities

Graph Inequalities on the Number Line

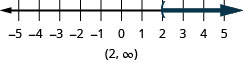
What number would make the inequality $x>3$ true? Are you thinking, "$x$ could be four"? That’s correct, but $x$ could be 6, too, or 37, or even 3.001. Any number greater than three is a solution to the inequality $x>3$. Thus the solution set to this inequality is an infinite set of numbers. We can show all the solutions to the inequality $x>3$ on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis or an open circle at three.

Interval Notation

We can also represent solutions sets for inequalities using interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket "[" when the set includes the endpoint and a parenthesis "(" to indicate that an endpoint is not included.

The conventions for sets written using interval notation are:

The smallest term (if there is one) from the interval is written first.
The largest term (if there is one) from the interval is written second, following a comma.
All real numbers between the smallest and largest term are included in the set.
Parentheses, "$($" or "$)$," are used to signify that an endpoint is not included, called exclusive.
Brackets, "$[$" or "$]$," are used to indicate that an endpoint is included, called inclusive.

In interval notation, we express the solution set for the inequality $x>3$ as $(3,\infty)$. There is no upper end to the solution to this inequality; the interval is unbounded. The symbol $\infty$ is read as “infinity.” It is not an actual number. Figure $\PageIndex{1}$ shows both the graph on the number line and, below it, the interval notation.

The figure shows the inquality, x is greater than 3, graphed on a number line from negative 5 to 5. There is shading that starts at 3 and extends to numbers to its right. The solution for the inequality is written in interval notation. It is the interval from 3 to infinity, not including 3. — Figure $\PageIndex{1}$: The inequality $x>3$ is graphed on this number line and written in interval notation.

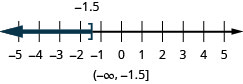
The inequality $x\leq 1$ means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at $x=1$. We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions (Figure $\PageIndex{2}$). There is no lower end to those numbers. We write $x\leq 1x\leq 1 $in interval notation as $(−\infty,1]$. The symbol $−\infty$ is read as “negative infinity.”

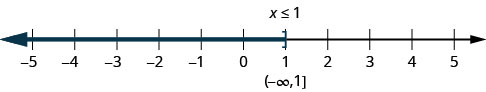
The figure shows the inquality, x is less than or equal to l, graphed on a number line from negative 5 to 5. There is shading that starts at 1 and extends to numbers to its left. The solution for the inequality is written in interval notation. It is the interval from negative infinity to one, including 1. — Figure $\PageIndex{2}$: The inequality $x\leq 1$ is graphed on this number line and written in interval notation.

Figure $\PageIndex{3}$ shows both the number line and interval notation.

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

$The figure shows that the solution of the inequality x is greater than a is indicated on a number line with a left parenthesis at a and shading to the right, and that the solution in interval notation is the interval from a to infinity enclosed in parentheses. It shows the solution of the inequality x is greater than or equal to a is indicated on a number line with an left bracket at a and shading to the right, and that the solution in interval notation is the interval a to infinity within a left bracket and right parenthesis. It shows that the solution of the inequality x is less than a is indicated on a number line with a right parenthesis at a and shading to the left, and that the solution in interval notation is the the interval negative infinity to a within parentheses. It shows that the solution of the inequality x is less than or equal to a is indicated on anumber line with a right bracket at a and shading to the left, and that the solution in interval notation is negative infinity to a within a left parenthesis and right bracket.$

The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals.

Example $\PageIndex{1}$

Graph each inequality on the number line and write in interval notation.

$x\geq −3$
$x<2.5$
$x\leq −\frac{3}{5}$

Answer

ⓐ

	$ x \geq -3 $
Shade to the right of $−3$, and put a bracket at $−3$.	$.$
Write in interval notation.	$ [-3, \infty) $

ⓑ

	$ x < 2.5 $
Shade to the left of 2.5 and put a parenthesis at 2.5.	$.$
Write in interval notation.	$ (-\infty, 2.5) $

ⓒ

	$ x \leq -\dfrac{3}{5} $
Shade to the left of $−\frac{3}{5}$, and put a bracket at $−\frac{3}{5}$.	$.$
Write in interval notation.	$ \bigg( -\infty, \dfrac{3}{5}\bigg] $

Example $\PageIndex{2}$

Graph each inequality on the number line and write in interval notation:

$x>2$
$x\leq −1.5$
$x\geq \frac{3}{4}$.

Answer

ⓐ

$The graph of the inequality x is greater than 2 is indicated on a number line with a left parenthesis at 2 and shading to the right. The solution in interval notation is the interval from 2 to infinity enclosed within parentheses.$

ⓑ

$The graph of the inequality x is less than or equal to negative 1.5 is indicated on a number line with a right bracket at negative 1.5 and shading to the left. The solution in interval notation is the interval from negative infinity to negative 1.5 enclosed within a left parenthesis and right bracket.$

ⓒ

$The graph of the inequality x is greater than or rqual to three-fourths is indicated on a number line with a left bracket at three-fourths and shading to the right. The solution in interval notation is the interval from three-fourths to infinity enclosed within a left bracket and left parentheses.$

Example $\PageIndex{3}$

Graph each inequality on the number line and write in interval notation:

$x\leq −4$
$x\geq 0.5$
$x<−\frac{2}{3}$.

Answer

ⓐ

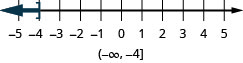
$The graph of the inequality x is less than or equal to negative 4 is indicated on a number line with a right bracket at negative 4 and shading to the left. The solution in interval notation is the interval from negative infinity to negative 4 enclosed within an left parenthesis and right bracket.$

ⓑ

$The graph of the inequality x is greater than or equal to 0.5 is indicated on a number line with a left bracket at 0.5 and shading to the right. The solution in interval notation is the interval from 0.5 to infinity enclosed within a left bracket and right parenthesis.$

ⓒ

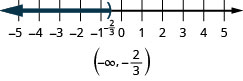
$The graph of the inequality x is less than negative two-thirds is indicated on a number line with a right parenthesis at negative two-thirds and shading to the left. The solution in interval notation is the interval from negative infinity to negative two-thirds enclosed within parentheses.$

What numbers are greater than two but less than five? Are you thinking say, $2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99$? We can represent all the numbers between two and five with the inequality $2<x<5$. We can show $2<x<5$ on the number line by shading all the numbers between two and five. Again, we use the parentheses to show the numbers two and five are not included. See Figure.

The graph of the inequality 2 is less than x which is less than 5 shows open circles a 2 and 5 and shading in between. — Figure $\PageIndex{3}$

Example $\PageIndex{4}$

Graph each inequality on the number line and write in interval notation.

ⓐ $−3<x<4$ ⓑ $−6\leq x<−1$ ⓒ $0\leq x\leq 2.5$

Answer

ⓐ

		$-3 < x < 4$
Shade between $−3$ and 4. Put a parentheses at $−3$ and 4.		$.$
Write in interval notation.		$ (-3,4) $

ⓑ

			$ -6 \leq x < -1 $
Shade between $−6$ and −1. Put a bracket at $−6$, and a parenthesis at −1.			$.$
Write in interval notation.			$ [-6,1) $

ⓒ

			$ 0 \leq x \leq 2.5 $
Shade between 0 and 2.5. Put a bracket at 0 and at 2.5.			$.$
Write in interval notation.			$ [0, 2.5] $

Example $\PageIndex{5}$

Graph each inequality on the number line and write in interval notation:

ⓐ $−2<x<1$ ⓑ $−5\leq x<−4$ ⓒ $1\leq x\leq 4.25$

Answer

ⓐ

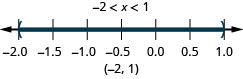
$Negative 2 is less x which is less than 1. There are open circles at negative 2 and 1 and shading between negative 2 and 1 on the number line. Put parentheses at negative 2 and 1. Write in interval notation.$

ⓑ

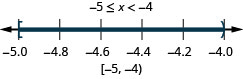
$Negative 5 is less than or equal to x which is less than negative 4. There is a closed circle at negative 6 and an open circle at negative 4 and shading between negative 5 and negative 4 on the number line. Put a bracket at negative 5 and a parenthesis at negative 4. Write in interval notation.$

ⓒ

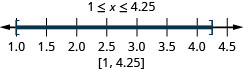
$1 is less than or equal to x which is less than 4.25. There is closed circle at 1 and a closed circle at 4.25 and shading between 1 and 4.25 on the number line. Put brackets at 1 and 4.25. Write in interval notation.$

Example $\PageIndex{6}$

Graph each inequality on the number line and write in interval notation:

ⓐ $−6<x<2$ ⓑ $−3\leq x< −1$ ⓒ $2.5\leq x\leq 6$

Answer

ⓐ

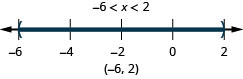
$Negative 6 is less than x which is less than 2. There is an open circle at negative 6 and an open circle at 2 and shading between negative 6 and 2 on the number line. Put parentheses at negative 6 and 2. Write in interval notation.$

ⓑ

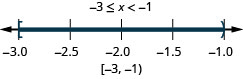
$Negative 3 is less than or equal to x which is less than negative 1. There is a closed circle at negative 3 and an open circle at negative 1 and shading between negative 3 and negative 1 on the number line. Put a bracket at negative 3 and a parenthesis at negative 1. Write in interval notation.$

ⓒ

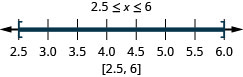
$2.5 is less than or equal to x which is less thanor equal to 6. There is a closed circle at 2.5 and a closed circle at 6 and shading between 2.5 and 6 on the number line. Put brackets at 2.5 and 6. Write in interval notation.$

Set-builder Notation

In the previous examples, we used interval notation to describe the solution set of an inequality. We can also describe the solution set in set-builder notation. For example, $\{x\;|\;10≤x<30\}$ describes the allowed values of $x$ in set-builder notation. The braces "$\{\}$" are read as “the set of,” and the vertical bar "$|$" is read as “such that,” so we would read$ \{x\;|\;10≤x<30\}$ as “the set of $x$-values such that 10 is less than or equal to $x$, and $x$ is less than 30.”

Figure $\PageIndex{4}$ compares inequality notation, set-builder notation, and interval notation.

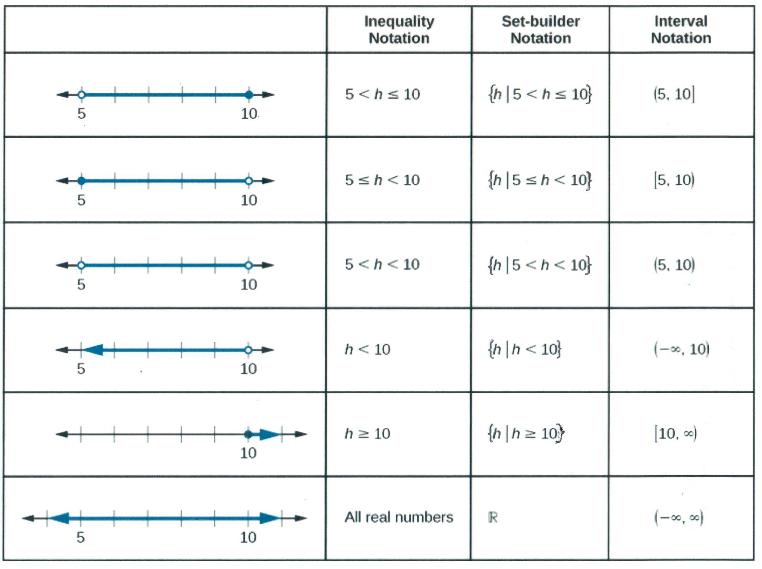
$clipboard_e29d19ab394e60c22f5cda847985a99e8.png$

Figure $\PageIndex{4}$: Summary of notations for inequalities, set-builder, and interval.

In set notation, there is a symbol $\cup$ to represent “or,” and we say we are taking the union of the two sets. We saw this in earlier examples, to combine two unconnected intervals. As another example, we can take the union of the sets$\{2,3,5\}$ and $\{4,5,6\}$: $\{2,3,5\} \cup \{4,6\} = \{2,3,4,5,6\}$. It is the set of all elements that belong to one or the other (or both) of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is

\[\{x\;|\; |x|≥3\}=\left(−\infty,−3\right]\cup\left[3,\infty\right)\]

Set-Builder Notation compared with Interval Notation

Set-builder notation is a method of specifying a set of elements that satisfy a certain condition. It takes the form$\{x|\text{ statement about } x\}$ which is read as “the set of all $x$ such that the statement about $x$ is true.” For example, we can write

\[\{x\;|\;4<x≤12\}, \nonumber\]

which is the set of all $x$ such that $x$ is greater than 4 and less than or equal to 12.

Interval notation is a way of describing sets that include all real numbers between a lower limit that may or may not be included and an upper limit that may or may not be included. The endpoint values are listed between brackets or parentheses. A square bracket indicates inclusion in the set, and a parenthesis indicates exclusion from the set. For example, the same set just given in set-builder notation can also be written in interval notation as

\[\left(4,12\right]. \nonumber\]

Solve Linear Inequalities

A linear inequality is much like a linear equation—but the equal sign is replaced with an inequality sign. A linear inequality is an inequality in one variable that can be written in one of the forms, $ax+b<c$, $ax+b\leq c$, $ax+b>c$, or $ax+b\geq c$.

LINEAR INEQUALITY

A linear inequality is an inequality in one variable that can be written in one of the following forms where $a, \, b,$ and $c$ are real numbers and $a≠0$:

\[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]

When we solved linear equations, we were able to use the properties of equality to add, subtract, multiply, or divide both sides and still keep the equality. Similar properties hold true for inequalities.

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality. For example:

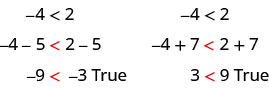
$Negative 4 is less than 2. Negative 4 minus 5 is less than 2 minus 5. Negative 9 is less than negative 3, which is true. Negative 4 is less than 2. Negative 4 plus 7 is less than 2 plus 7. 3 is less than 9, which is true.$

Notice that the inequality sign stayed the same.

This leads us to the Addition and Subtraction Properties of Inequality.

ADDITION AND SUBTRACTION PROPERTY OF INEQUALITY

For any numbers $a, \, b,$ and $c,$ if $a<b$, then

\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]

We can add or subtract the same quantity from both sides of an inequality and still keep the inequality

What happens to an inequality when we divide or multiply both sides by a constant?

Let’s first multiply and divide both sides by a positive number.

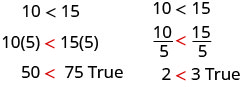
$10 is less than 15. 10 times 5 is less than 15 times 5. 50 is less than 75 is true. 10 is less than 15. 10 divided by 5 is less than 15 divided by 5. 2 is less than 3 is true.$

The inequality signs stayed the same.

Does the inequality stay the same when we divide or multiply by a negative number?

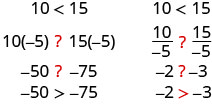
$10 is less than 15 10 times negative 5 is blank 15 times negative 5? Negative 50 is blank negative 75. Negative 50 is greater than negative 75. 10 is less than 15. 10 divided by negative 5 is blank 15 divided by negative 5. Negative 2 is blank negative 3. Negative 2 is blank negative 3.$

Notice that when we filled in the inequality signs, the inequality signs reversed their direction.

When we divide or multiply an inequality by a positive number, the inequality sign stays the same. When we divide or multiply an inequality by a negative number, the inequality sign reverses.

This gives us the Multiplication and Division Property of Inequality.

MULTIPLICATION AND DIVISION PROPERTY OF INEQUALITY

For any numbers $a, \, b,$ and $c,$

\[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]

When we divide or multiply an inequality by $a$:

positive number, the inequality stays the same.
negative number, the inequality reverses.

Sometimes when solving an inequality, as in the next example, the variable ends upon the right. We can rewrite the inequality in reverse to get the variable to the left.

\[x>a \text{ has the same meaning as } a<x \nonumber \]

Think about it as “If Xander is taller than Andy, then Andy is shorter than Xander.”

Example $\PageIndex{7}$

Solve each inequality. Graph the solution on the number line, and write the solution in interval notation.

ⓐ $x−\frac{3}{8}\leq \frac{3}{4}$ ⓑ $9y<54$ ⓒ $−15<\frac{3}{5}z$

Answer

ⓐ

	$.$
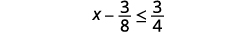
Add 3838 to both sides of the inequality.
Simplify.
Graph the solution on the number line.	$.$
Write the solution in interval notation.	$.$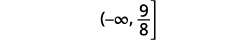

ⓑ

	$.$
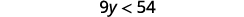
Divide both sides of the inequality by 9; since 9 is positive, the inequality stays the same.
Simplify.	$.$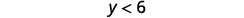
Graph the solution on the number line.	$.$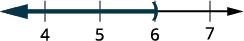
Write the solution in interval notation.	$.$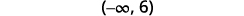

ⓒ

	$.$
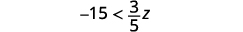
Multiply both sides of the inequality by $\frac{5}{3}$. Since $\frac{5}{3}$ is positive, the inequality stays the same.
Simplify.
Rewrite with the variable on the left.
Graph the solution on the number line.	$.$
Write the solution in interval notation.

Example $\PageIndex{8}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $p−\frac{3}{4}\geq \frac{1}{6}$ ⓑ $9c>72$ ⓒ $24\leq \frac{3}{8}m$

Answer

ⓐ

$p is less than eleven-twelfths. The solution on the number line has a right bracket at eleven-twelfths with shading to the right. The solution in interval notation is, eleven-twelfths to infinity within a bracket and parenthesis.$

ⓑ

c is less than 8. The solution on the number line has a left bracket at 8 with shading to the right. The solution in interval notation is, 8 to infinity within parentheses.

ⓒ

$m is greater than or equal to 8. The solution on the number line has a right bracket at 64 with shading to the right. The solution in interval notation is, 64 to infinity within a bracket and parentheses.$

Example $\PageIndex{9}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $r−\frac{1}{3}\leq \frac{7}{12}$ ⓑ $12d\leq 60$ ⓒ $−24<\frac{4}{3}n$

Answer

ⓐ

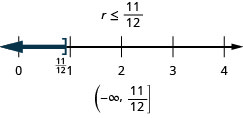
$r is less than or equal to eleven-twelfths. The solution on the number line has a left bracket at eleven-twelfths with shading to the left. The solution in interval notation is negative infinity to eleven-twelfths within a parenthesis and a bracket.$

ⓑ

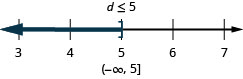
$c is less than or equal to 5. The solution on the number line has a right bracket at 5 with shading to the left. The solution in interval notation is negative infinity to 5 within a parentheses and a bracket.$

ⓒ

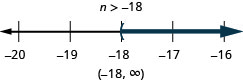
$n is greater than negative 18. The solution on the number line has a left parenthesis at negative 18 with shading to the right. The solution in interval notation is negative 18 to infinity within parentheses.$

Be careful when you multiply or divide by a negative number—remember to reverse the inequality sign.

Example $\PageIndex{10}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation.

ⓐ $−\frac{1}{3}m\geq \frac{6}{5}$ ⓑ $\frac{n}{−2} \geq 8$

Answer

ⓐ

	$.$
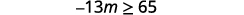
Divide both sides of the inequality by $−\frac{1}{3}$. Since $−\frac{1}{3}$ is a negative, the inequality reverses.	$.$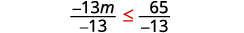
Simplify.	$.$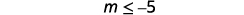
Graph the solution on the number line.	$.$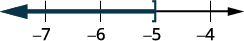
Write the solution in interval notation.	$.$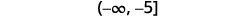

ⓑ

	$.$
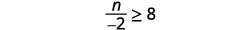
Multiply both sides of the inequality by $−2$. Since $−2$ is a negative, the inequality reverses.	$.$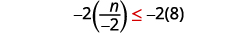
Simplify.	$.$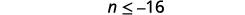
Graph the solution on the number line.	$.$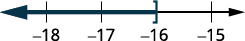
Write the solution in interval notation.	$.$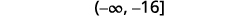

Example $\PageIndex{11}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $−8q<32$ ⓑ $\frac{k}{−12} \leq 15$.

Answer

ⓐ

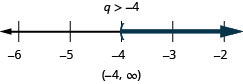
$q is greater than or equal to negative 4. The solution on the number line has a left parenthesis at negative 4 with shading to the right. The solution in interval notation is negative 4 to infinity within parentheses.$

ⓑ

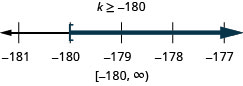
$k is greater than or equal to negative 180. The solution on the number line has a left bracket at negative 180 with shading to the right. The solution in interval notation is negative 180 to infinity within a bracket and a parenthesis.$

Example $\PageIndex{12}$

Solve each inequality, graph the solution on the number line, and write the solution in interval notation:

ⓐ $−7r\leq −70$ ⓑ $\frac{u}{−4}\geq −16$.

Answer

ⓐ

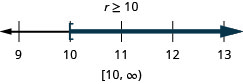
$r is greater than or equal to 10. The solution on the number line has a left bracket at 10 with shading to the right. The solution in interval notation is 10 to infinity within a bracket and parenthesis.$

ⓑ

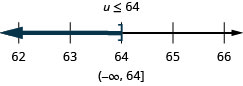
$u is less than or equal to 64. The solution on the number line has a right bracket at 64 with shading to the left. The solution in interval notation is negative infinity to 64 within parenthesis and a bracket.$

Most inequalities will take more than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, but make sure to pay close attention when we multiply or divide to isolate the variable.

Example $\PageIndex{13}$

Solve the inequality $6y\leq 11y+17$, graph the solution on the number line, and write the solution in interval notation.

Answer

	$.$
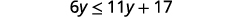
Subtract 11y11y from both sides to collect the variables on the left.	$.$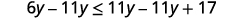
Simplify.	$.$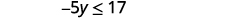
Divide both sides of the inequality by −5,−5, and reverse the inequality.
Simplify.	$.$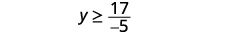
Graph the solution on the number line.	$.$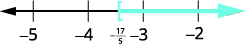
Write the solution in interval notation.	$.$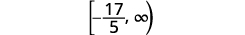

Example $\PageIndex{14}$

Solve the inequality, graph the solution on the number line, and write the solution in interval notation: $3q\geq 7q−23$.

Answer: $q is less than or equal to 23 divided by 4. The solution on the number line has a right bracket at 23 divided by 4 with shading to the left. The solution in interval notation is negative infinity to 23 divided by 4 within a parenthesis and a bracket.$

Example $\PageIndex{15}$

Solve the inequality, graph the solution on the number line, and write the solution in interval notation: $6x<10x+19$.

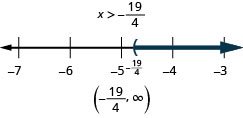
Answer: $x is greater than negative 19 divided by 4. The solution on the number line has a left parenthesis at negative 19 divided by 4 with shading to the right. The solution in interval notation is negative 19 divided by 4 to infinity within parentheses.$

When solving inequalities, it is usually easiest to collect the variables on the side where the coefficient of the variable is largest. This eliminates negative coefficients and so we don’t have to multiply or divide by a negative—which means we don’t have to remember to reverse the inequality sign.

Example $\PageIndex{16}$

Solve the inequality $8p+3(p−12)>7p−28$, graph the solution on the number line, and write the solution in interval notation.

Answer

	$8p+3(p−12)>7p−28$
Simplify each side as much as possible.
Distribute.	$8p+3p−36>7p−28$
Combine like terms.	$11p−36>7p−28$
Subtract $7p$ from both sides to collect the variables on the left, since $11>7$.	$11p−36−7p>7p−28−7p$
Simplify.	$4p−36>−28$
Add $36$ to both sides to collect the constants on the right.	$4p−36+36>−28+36$
Simplify.	$4p>8$
Divide both sides of the inequality by $4$; the inequality stays the same.	$\dfrac{4p}{4}>\dfrac{8}{4}$
Simplify.	$p>2$
Graph the solution on the number line.
Write the solution in interval notation.	$(2,\infty)$

Example $\PageIndex{17}$

Solve the inequality $9y+2(y+6)>5y−24$, graph the solution on the number line, and write the solution in interval notation.

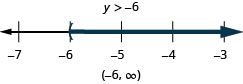
Answer: $y is greater than negative 6. The solution on the number line has a left parenthesis at negative 6 with shading to the right. The solution in interval notation is negative 6 to infinity within parentheses.$

Example $\PageIndex{18}$

Solve the inequality $6u+8(u−1)>10u+32$, graph the solution on the number line, and write the solution in interval notation.

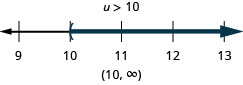
Answer: $u is greater than negative 10. The solution on the number line has a left parenthesis at 10 with shading to the right. The solution in interval notation is 10 to infinity within parentheses.$

Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, too. We recognize these forms when we are left with only constants as we solve the inequality. If the result is a true statement, we have an identity. If the result is a false statement, we have a contradiction.

Example $\PageIndex{19}$

Solve the inequality $8x−2(5−x)<4(x+9)+6x$, graph the solution on the number line, and write the solution in interval notation.

Answer

Simplify each side as much as possible.		$8x−2(5−x)<4(x+9)+6x$
Distribute.		$8x−10+2x<4x+36+6x$
Combine like terms.		$10x−10<10x+36$
Subtract ${\color{red}{10x}}$ from both sides to collect the variables on the left.		$10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}$
Simplify.		$−10<36$
The $x$'s are gone, and we have a true statement.		The inequality is an identity. The solution is all real numbers.
Graph the solution on the number line.		$.$
Write the solution in interval notation.		$(−\infty,\infty)$

Example $\PageIndex{20}$

Solve the inequality $4b−3(3−b)>5(b−6)+2b$, graph the solution on the number line, and write the solution in interval notation.

Answer

Example $\PageIndex{21}$

Solve the inequality $9h−7(2−h)<8(h+11)+8h$, graph the solution on the number line, and write the solution in interval notation.

Answer: $The inequality is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

We can clear fractions in inequalities much as we did in equations. Again, be careful with the signs when multiplying or dividing by a negative.

Example $\PageIndex{22}$

Solve the inequality $\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$, graph the solution on the number line, and write the solution in interval notation.

Answer

	$\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}$
Multiply both sides by the LCD, 24, to clear the fractions.	${\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)$
Simplify.	$ 8a - 3a > 5a + 18 $
Combine like terms.	$ 5a > 5a + 18$
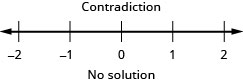
Subtract $5a$ from both sides to collect the variables on the left.	$ 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18$
Simplify.	$0 > 18 $
The statement is false.	The inequality is a contradiction. There is no solution.
Graph the solution on the number line.	$.$
Write the solution in interval notation.	There is no solution.

Example $\PageIndex{23}$

Solve the inequality $\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}$, graph the solution on the number line, and write the solution in interval notation.

Answer: $The inequality is a contradiction. So, there is no solution. As a result, there is no graph on the number line or interval notation.$

Example $\PageIndex{24}$

Solve the inequality $\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}$, graph the solution on the number line, and write the solution in interval notation.

Answer: $The inequality is a contradiction. So, there is no solution. As a result, there is no graph on the number line or interval notation.$

Translate to an Inequality and Solve

To translate English sentences into inequalities, we need to recognize the phrases that indicate the inequality. Some words are easy, like “more than” and “less than.” But others are not as obvious. Table shows some common phrases that indicate inequalities.

$>$	$\geq$	$<$	$\leq$
is greater than is more than is larger than exceeds	is greater than or equal to is at least is no less than is the minimum	is less than is smaller than has fewer than is lower than	is less than or equal to is at most is no more than is the maximum

Example $\PageIndex{25}$

Translate and solve. Then graph the solution on the number line, and write the solution in interval notation.

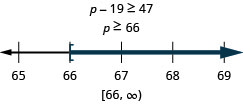
\[\text{Twenty-seven less than }x\text{ is at least }48.\nonumber\]

Answer

	$.$
Translate.	$x - 27 \geq 48$
Solve—add 27 to both sides.	$ x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}$
Simplify.	$x \geq 75$
Graph on the number line.	$.$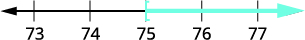
Write in interval notation.	$[75, \infty)$

Example $\PageIndex{26}$

Translate and solve. Then graph the solution on the number line, and write the solution in interval notation.

\[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]

Answer: $p minus 19 is greater than or equal to 47. Its solution is p is greater than or equal to 66. The solution on the number line has a left bracket at 66 with shading to the right. The solution in interval notation is 66 to infinity within a bracket and a parenthesis.$

Example $\PageIndex{27}$

Translate and solve. Then graph the solution on the number line, and write the solution in interval notation.

\[\text{Four more than }a\text{ is at most }15.\nonumber\]

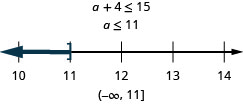
Answer: $a plus 4 is less than or equal to 15. Its solution is a is less than or equal to 11. The solution on the number line has a right bracket at 11with shading to the left. The solution in interval notation is negative infinity to 11 within a parenthesis and bracket.$

Solve Applications with Linear Inequalities

Many real-life situations require us to solve inequalities. The method we will use to solve applications with linear inequalities is very much like the one we used when we solved applications with equations.

We will read the problem and make sure all the words are understood. Next, we will identify what we are looking for and assign a variable to represent it. We will restate the problem in one sentence to make it easy to translate into an inequality. Then, we will solve the inequality.

Sometimes an application requires the solution to be a whole number, but the algebraic solution to the inequality is not a whole number. In that case, we must round the algebraic solution to a whole number. The context of the application will determine whether we round up or down.

Example $\PageIndex{28}$

Dawn won a mini-grant of $4,000 to buy tablet computers for her classroom. The tablets she would like to buy cost $254.12 each, including tax and delivery. What is the maximum number of tablets Dawn can buy?

Answer: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}\)

Example $\PageIndex{29}$

Angie has $20 to spend on juice boxes for her son’s preschool picnic. Each pack of juice boxes costs $2.63. What is the maximum number of packs she can buy?

Answer: Angie can buy 7 packs of juice.

Example $\PageIndex{30}$

Daniel wants to surprise his girlfriend with a birthday party at her favorite restaurant. It will cost $42.75 per person for dinner, including tip and tax. His budget for the party is $500. What is the maximum number of people Daniel can have at the party?

Answer: Daniel can have 11 people at the party.

Example $\PageIndex{31}$

Taleisha’s phone plan costs her $28.80 a month plus $0.20 per text message. How many text messages can she send/receive and keep her monthly phone bill no more than $50?

Answer: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)

Example $\PageIndex{32}$

Sergio and Lizeth have a very tight vacation budget. They plan to rent a car from a company that charges $75 a week plus $0.25 a mile. How many miles can they travel during the week and still keep within their $200 budget?

Answer: Sergio and Lizeth can travel no more than 500 miles.

Example $\PageIndex{33}$

Rameen’s heating bill is $5.42 per month plus $1.08 per therm. How many therms can Rameen use if he wants his heating bill to be a maximum of $87.50.

Answer: Rameen’s heating bill is $5.42 per month plus $1.08 per therm. How many therms can Rameen use if he wants his heating bill to be a maximum of $87.50.

Profit is the money that remains when the costs have been subtracted from the revenue. In the next example, we will find the number of jobs a small businesswoman needs to do every month in order to make a certain amount of profit.

Example $\PageIndex{34}$

Felicity has a calligraphy business. She charges $2.50 per wedding invitation. Her monthly expenses are $650. How many invitations must she write to earn a profit of at least $2,800 per month?

Answer: \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}\)

Example $\PageIndex{35}$

Caleb has a pet sitting business. He charges $32 per hour. His monthly expenses are $2,272. How many hours must he work in order to earn a profit of at least $800 per month?

Answer: Caleb must work at least 96 hours.

Example $\PageIndex{36}$

Elliot has a landscape maintenance business. His monthly expenses are $1,100. If he charges $60 per job, how many jobs must he do to earn a profit of at least $4,000 a month?

Answer: Elliot must work at least 85 jobs.

There are many situations in which several quantities contribute to the total expense. We must make sure to account for all the individual expenses when we solve problems like this.

Example $\PageIndex{37}$

Malik is planning a six-day summer vacation trip. He has $840 in savings, and he earns $45 per hour for tutoring. The trip will cost him $525 for airfare, $780 for food and sightseeing, and $95 per night for the hotel. How many hours must he tutor to have enough money to pay for the trip?

Answer: \(\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}\)

Example $\PageIndex{38}$

Brenda’s best friend is having a destination wedding and the event will last three days. Brenda has $500 in savings and can earn $15 an hour babysitting. She expects to pay $350 airfare, $375 for food and entertainment and $60 a night for her share of a hotel room. How many hours must she babysit to have enough money to pay for the trip?

Answer: Brenda must babysit at least 27 hours.

Example $\PageIndex{39}$

Josue wants to go on a 10-night road trip with friends next spring. It will cost him $180 for gas, $450 for food, and $49 per night to share a motel room. He has $520 in savings and can earn $30 per driveway shoveling snow. How many driveways must he shovel to have enough money to pay for the trip?

Answer: Josue must shovel at least 20 driveways.

Key Concepts

Inequalities, Number Lines, and Interval Notation
$x>a \quad x\geq a\quad x<a\quad x\leq a$
$The figure shows that the solution of the inequality x is greater than a is indicated on a number line with a left parenthesis at a and shading to the right, and that the solution in interval notation is the interval from a to infinity enclosed in parentheses. It shows the solution of the inequality x is greater than or equal to a is indicated on a number line with an left bracket at a and shading to the right, and that the solution in interval notation is the interval a to infinity within a left bracket and right parenthesis. It shows that the solution of the inequality x is less than a is indicated on a number line with a right parenthesis at a and shading to the left, and that the solution in interval notation is the the interval negative infinity to a within parentheses. It shows that the solution of the inequality x is less than or equal to a is indicated on anumber line with a right bracket at a and shading to the left, and that the solution in interval notation is negative infinity to a within a left parenthesis and right bracket.$
Linear Inequality
- A linear inequality is an inequality in one variable that can be written in one of the following forms where a, b, and care real numbers and $a\neq 0$:
  \[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]
Addition and Subtraction Property of Inequality
- For any numbers a, b, and c, if a<b,thena<b,then
  \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]
- We can add or subtract the same quantity from both sides of an inequality and still keep the inequality.
Multiplication and Division Property of Inequality
- For any numbers a, b, and c,
  $\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}$

Phrases that indicate inequalities

$>$	$\geq$	$<$	$\leq$
is greater than is more than is larger than exceeds	is greater than or equal to is at least is no less than is the minimum	is less than is smaller than has fewer than is lower than	is less than or equal to is at most is no more than is the maximum

	\( x \geq -3 \)
Shade to the right of \(−3\), and put a bracket at \(−3\).	$.$
Write in interval notation.	\( [-3, \infty) \)

	\( x \leq -\dfrac{3}{5} \)
Shade to the left of \(−\frac{3}{5}\), and put a bracket at \(−\frac{3}{5}\).	$.$
Write in interval notation.	\( \bigg( -\infty, \dfrac{3}{5}\bigg] \)

		\(-3 < x < 4\)
Shade between \(−3\) and 4. Put a parentheses at \(−3\) and 4.		$.$
Write in interval notation.		\( (-3,4) \)

			\( -6 \leq x < -1 \)
Shade between \(−6\) and −1. Put a bracket at \(−6\), and a parenthesis at −1.			$.$
Write in interval notation.			\( [-6,1) \)

	\(8p+3(p−12)>7p−28\)
Simplify each side as much as possible.
Distribute.	\(8p+3p−36>7p−28\)
Combine like terms.	\(11p−36>7p−28\)
Subtract \(7p\) from both sides to collect the variables on the left, since \(11>7\).	\(11p−36−7p>7p−28−7p\)
Simplify.	\(4p−36>−28\)
Add \(36\) to both sides to collect the constants on the right.	\(4p−36+36>−28+36\)
Simplify.	\(4p>8\)
Divide both sides of the inequality by \(4\); the inequality stays the same.	\(\dfrac{4p}{4}>\dfrac{8}{4}\)
Simplify.	\(p>2\)
Graph the solution on the number line.
Write the solution in interval notation.	\((2,\infty)\)

Search

Text Color

Text Size

Margin Size

Font Type

Interval Notation

Set-builder Notation

	\( x < 2.5 \)
Shade to the left of 2.5 and put a parenthesis at 2.5.	$.$
Write in interval notation.	\( (-\infty, 2.5) \)

			\( 0 \leq x \leq 2.5 \)
Shade between 0 and 2.5. Put a bracket at 0 and at 2.5.			$.$
Write in interval notation.			\( [0, 2.5] \)

	$.$
Divide both sides of the inequality by \(−\frac{1}{3}\). Since \(−\frac{1}{3}\) is a negative, the inequality reverses.	$.$
Simplify.	$.$
Graph the solution on the number line.	$.$
Write the solution in interval notation.	$.$

Simplify each side as much as possible.		\(8x−2(5−x)<4(x+9)+6x\)
Distribute.		\(8x−10+2x<4x+36+6x\)
Combine like terms.		\(10x−10<10x+36\)
Subtract \({\color{red}{10x}}\) from both sides to collect the variables on the left.		\(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\)
Simplify.		\(−10<36\)
The \(x\)'s are gone, and we have a true statement.		The inequality is an identity. The solution is all real numbers.
Graph the solution on the number line.		$.$
Write the solution in interval notation.		\((−\infty,\infty)\)

	\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)
Multiply both sides by the LCD, 24, to clear the fractions.	\({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\)
Simplify.	\( 8a - 3a > 5a + 18 \)
Combine like terms.	\( 5a > 5a + 18\)
Subtract \(5a\) from both sides to collect the variables on the left.	\( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\)
Simplify.	\(0 > 18 \)
The statement is false.	The inequality is a contradiction. There is no solution.
Graph the solution on the number line.	$.$
Write the solution in interval notation.	There is no solution.

	$.$
Translate.	\(x - 27 \geq 48\)
Solve—add 27 to both sides.	\( x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\)
Simplify.	\(x \geq 75\)
Graph on the number line.	$.$
Write in interval notation.	\([75, \infty)\)