Section 2.6E: Exercises
- Last updated
- Jan 17, 2020
- Save as PDF
- Page ID
- 33039
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Graph Inequalities on the Number Line
In the following exercises, graph each inequality on the number line and write in interval notation.
ⓐ x<−2
ⓑ x≥−3.5
ⓒ x≤23
ⓐ x>3
ⓑ x≤−0.5
ⓒ x≥13
- Answer
-
ⓐ

ⓑ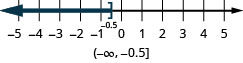
ⓒ

ⓐ x≥−4
ⓑ x<2.5
ⓒ x>−32
ⓐ x≤5
ⓑ x≥−1.5
ⓒ x<−73
- Answer
-
ⓐ

ⓑ
ⓒ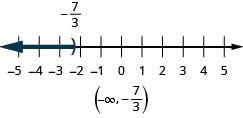
ⓐ −5<x<2
ⓑ −3≤x<−1
ⓒ 0≤x≤1.5
ⓐ −2<x<0
ⓑ −5≤x<−3
ⓒ 0≤x≤3.5
- Answer
-
ⓐ

ⓑ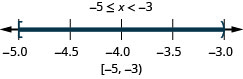
ⓒ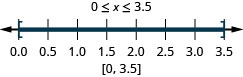
ⓐ −1<x<3
ⓑ −3<x≤−2
ⓒ −1.25≤x≤0
ⓐ −4<x<2
ⓑ −5<x≤−2
ⓒ −3.75≤x≤0
- Answer
-
ⓐ

ⓑ
ⓒ
Solve Linear Inequalities
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
ⓐ a+34≥710
ⓑ 8x>72
ⓒ 20>25h
ⓐ b+78≥16
ⓑ 6y<48
ⓒ 40<58k
- Answer
-
ⓐ
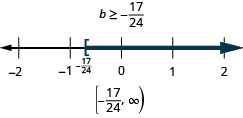
ⓑ
ⓒ
ⓐ f−1320<−512
ⓑ 9t≥−27
ⓒ 76j≥42
ⓐ g−1112<−518
ⓑ 7s<−28
ⓒ 94g≤36
- Answer
-
ⓐ
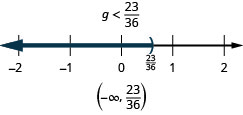
ⓑ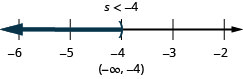
ⓒ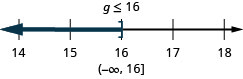
ⓐ −5u≥65
ⓑ a−3≤9
ⓐ −8v≤96
ⓑ b−10≥30
- Answer
-
ⓐ
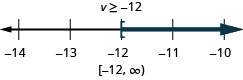
ⓑ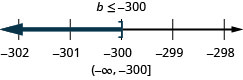
ⓐ −9c<126
ⓑ −25<p−5
ⓐ −7d>105
ⓑ −18>q−6
- Answer
-
ⓐ
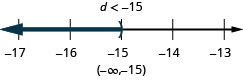
ⓑ
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
4v≥9v−40
5u≤8u−21
- Answer
-

13q<7q−29
9p>14p−18
- Answer
-

12x+3(x+7)>10x−24
9y+5(y+3)<4y−35
- Answer
-

6h−4(h−1)≤7h−11
4k−(k−2)≥7k−26
- Answer
-
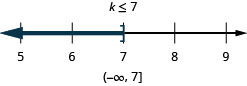
8m−2(14−m)≥7(m−4)+3m
6n−12(3−n)≤9(n−4)+9n
- Answer
-
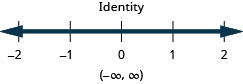
34b−13b<512b−12
9u+5(2u−5)≥12(u−1)+7u
- Answer
-
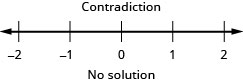
23g−12(g−14)≤16(g+42)
45h−23(h−9)≥115(2h+90)
- Answer
-
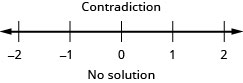
56a−14a>712a+23
12v+3(4v−1)≤19(v−2)+5v
- Answer
-

In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
15k≤−40
35k≥−77
- Answer
-

23p−2(6−5p)>3(11p−4)
18q−4(10−3q)<5(6q−8)
- Answer
-
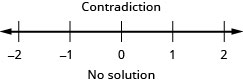
−94x≥−512
−218y≤−1528
- Answer
-
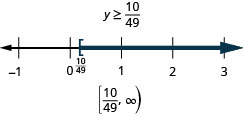
c+34<−99
d+29>−61
- Answer
-
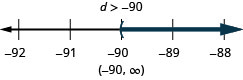
m18≥−4
n13≤−6
- Answer
-

Translate to an Inequality and Solve
In the following exercises, translate and solve. Then graph the solution on the number line and write the solution in interval notation.
Three more than h is no less than 25.
Six more than k exceeds 25.
- Answer
-

Ten less than w is at least 39.
Twelve less than x is no less than 21.
- Answer
-
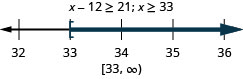
Negative five times r is no more than 95.
Negative two times s is lower than 56.
- Answer
-
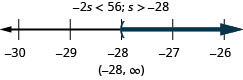
Nineteen less than b is at most −22.
Fifteen less than a is at least −7.
- Answer
-

Solve Applications with Linear Inequalities
In the following exercises, solve.
Alan is loading a pallet with boxes that each weighs 45 pounds. The pallet can safely support no more than 900 pounds. How many boxes can he safely load onto the pallet?
The elevator in Yehire’s apartment building has a sign that says the maximum weight is 2100 pounds. If the average weight of one person is 150 pounds, how many people can safely ride the elevator?
- Answer
-
A maximum of 14 people can safely ride in the elevator.
Andre is looking at apartments with three of his friends. They want the monthly rent to be no more than $2,360. If the roommates split the rent evenly among the four of them, what is the maximum rent each will pay?
Arleen got a $20 gift card for the coffee shop. Her favorite iced drink costs $3.79. What is the maximum number of drinks she can buy with the gift card?
- Answer
-
five drinks
Teegan likes to play golf. He has budgeted $60 next month for the driving range. It costs him $10.55 for a bucket of balls each time he goes. What is the maximum number of times he can go to the driving range next month?
Ryan charges his neighbors $17.50 to wash their car. How many cars must he wash next summer if his goal is to earn at least $1,500?
- Answer
-
86 cars
Keshad gets paid $2,400 per month plus 6% of his sales. His brother earns $3,300 per month. For what amount of total sales will Keshad’s monthly pay be higher than his brother’s monthly pay?
Kimuyen needs to earn $4,150 per month in order to pay all her expenses. Her job pays her $3,475 per month plus 4% of her total sales. What is the minimum Kimuyen’s total sales must be in order for her to pay all her expenses?
- Answer
-
$16,875
Andre has been offered an entry-level job. The company offered him $48,000 per year plus 3.5% of his total sales. Andre knows that the average pay for this job is $62,000. What would Andre’s total sales need to be for his pay to be at least as high as the average pay for this job?
Nataly is considering two job offers. The first job would pay her $83,000 per year. The second would pay her $66,500 plus 15% of her total sales. What would her total sales need to be for her salary on the second offer be higher than the first?
- Answer
-
$110,000
Jake’s water bill is $24.80 per month plus $2.20 per ccf (hundred cubic feet) of water. What is the maximum number of ccf Jake can use if he wants his bill to be no more than $60?
Kiyoshi’s phone plan costs $17.50 per month plus $0.15 per text message. What is the maximum number of text messages Kiyoshi can use so the phone bill is no more than $56.60?
- Answer
-
260 messages
Marlon’s TV plan costs $49.99 per month plus $5.49 per first-run movie. How many first-run movies can he watch if he wants to keep his monthly bill to be a maximum of $100?
Kellen wants to rent a banquet room in a restaurant for her cousin’s baby shower. The restaurant charges $350 for the banquet room plus $32.50 per person for lunch. How many people can Kellen have at the shower if she wants the maximum cost to be $1,500?
- Answer
-
35 people
Moshde runs a hairstyling business from her house. She charges $45 for a haircut and style. Her monthly expenses are $960. She wants to be able to put at least $1,200 per month into her savings account order to open her own salon. How many “cut & styles” must she do to save at least $1,200 per month?
Noe installs and configures software on home computers. He charges $125 per job. His monthly expenses are $1,600. How many jobs must he work in order to make a profit of at least $2,400?
- Answer
-
32 jobs
Katherine is a personal chef. She charges $115 per four-person meal. Her monthly expenses are $3,150. How many four-person meals must she sell in order to make a profit of at least $1,900?
Melissa makes necklaces and sells them online. She charges $88 per necklace. Her monthly expenses are $3,745. How many necklaces must she sell if she wants to make a profit of at least $1,650?
- Answer
-
62 necklaces
Five student government officers want to go to the state convention. It will cost them $110 for registration, $375 for transportation and food, and $42 per person for the hotel. There is $450 budgeted for the convention in the student government savings account. They can earn the rest of the money they need by having a car wash. If they charge $5 per car, how many cars must they wash in order to have enough money to pay for the trip?
Cesar is planning a four-day trip to visit his friend at a college in another state. It will cost him $198 for airfare, $56 for local transportation, and $45 per day for food. He has $189 in savings and can earn $35 for each lawn he mows. How many lawns must he mow to have enough money to pay for the trip?
- Answer
-
seven lawns
Alonzo works as a car detailer. He charges $175 per car. He is planning to move out of his parents’ house and rent his first apartment. He will need to pay $120 for application fees, $950 for security deposit, and first and last months’ rent at $1,140 per month. He has $1,810 in savings. How many cars must he detail to have enough money to rent the apartment?
Eun-Kyung works as a tutor and earns $60 per hour. She has $792 in savings. She is planning an anniversary party for her parents. She would like to invite 40 guests. The party will cost her $1,520 for food and drinks and $150 for the photographer. She will also have a favor for each of the guests, and each favor will cost $7.50. How many hours must she tutor to have enough money for the party?
- Answer
-
20 hours
Everyday Math
Maximum load on a stage In 2014, a high school stage collapsed in Fullerton, California, when 250 students got on stage for the finale of a musical production. Two dozen students were injured. The stage could support a maximum of 12,750 pounds. If the average weight of a student is assumed to be 140 pounds, what is the maximum number of students who could safely be on the stage?
Maximum weight on a boat In 2004, a water taxi sank in Baltimore harbor and five people drowned. The water taxi had a maximum capacity of 3,500 pounds (25 people with average weight 140 pounds). The average weight of the 25 people on the water taxi when it sank was 168 pounds per person. What should the maximum number of people of this weight have been?
- Answer
-
20 people
Wedding budget Adele and Walter found the perfect venue for their wedding reception. The cost is $9850 for up to 100 guests, plus $38 for each additional guest. How many guests can attend if Adele and Walter want the total cost to be no more than $12,500?
Shower budget Penny is planning a baby shower for her daughter-in-law. The restaurant charges $950 for up to 25 guests, plus $31.95 for each additional guest. How many guests can attend if Penny wants the total cost to be no more than $1,500?
- Answer
-
42 guests
Writing Exercises
Explain why it is necessary to reverse the inequality when solving −5x>10.
Explain why it is necessary to reverse the inequality when solving n−3<12.
- Answer
-
Answers will vary.
Find your last month’s phone bill and the hourly salary you are paid at your job. Calculate the number of hours of work it would take you to earn at least enough money to pay your phone bill by writing an appropriate inequality and then solving it. Do you feel this is an appropriate number of hours? Is this the appropriate phone plan for you?
Find out how many units you have left, after this term, to achieve your college goal and estimate the number of units you can take each term in college. Calculate the number of terms it will take you to achieve your college goal by writing an appropriate inequality and then solving it. Is this an acceptable number of terms until you meet your goal? What are some ways you could accelerate this process?
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?


