10.2 Polynomial and Radical Expressions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Polynomials
A term is a constant or the product of a constant and one or more variables. A monomial is an algebraic expression with one term. When it is of the form axn, where a is a constant, n is a whole number, and x is a variable, it is called a monomial in one variable.
A monomial, or two or more monomials combined by addition or subtraction, is a polynomial. Some polynomials have special names, based on the number of terms. A monomial is a polynomial with exactly one term. A binomial has exactly two terms, and a trinomial has exactly three terms. There are no special names for polynomials with more than three terms.
Definition: POLYNOMIALS
- polynomial—A monomial, or two or more algebraic terms combined by addition or subtraction
- monomial—A polynomial with exactly one term
- binomial—A polynomial with exactly two terms
- trinomial—A polynomial with exactly three terms
Every monomial, binomial, and trinomial is also a polynomial. They are just special members of the “family” of polynomials and so they have special names.
The degree of a polynomial and the degree of each of its terms are determined by the exponents of the variable. A monomial that is just a constant is a special case. The degree of a constant is 0.
Definition: DEGREE OF A POLYNOMIAL
- The degree of a term is the sum of the exponents of its variables.
- The degree of a constant is 0.
- The degree of a polynomial is the highest degree of all its terms.
Working with polynomials is easier when you list the terms in descending order of degrees. When a polynomial is written this way, it is said to be in standard form. Get in the habit of writing the term with the highest degree first.
Example 1
Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial. Then find the degree of each polynomial.
- 7y2−5y+3
- −2a4b2
- 3x5−4x3−6x2+x−8
- 2y−8xy3
- 15
- Solution
-
Polynomial Number of terms Type Degree of terms Degree of polynomial a. 7y2−5y+3 3 Trinomial 2, 1, 0 2 b. −2a4b2 1 Monomial 4 + 2 6 c. 3x5−4x3−6x2+x−8 5 Polynomial 5, 3, 2, 1, 0 5 d. 2y−8xy3 2 Binomial 1, 4 4 e. 15 1 Monomial 0 0
Adding and Subtracting Polynomials
We can think of adding and subtracting polynomials as just combining and simplifying two or more polynomials by combining like terms. Remember, like terms must have the same variables with the same exponent. Look for the like terms—those with the same variables and the same exponent. The Commutative Property of Addition allows us to rearrange the terms to put like terms together.
Example 2
Find the sum: (7y2−2y+9)+(4y2−8y−7).
Solution
Identify like terms.(7y2__−2y_+9)+(4y2__−8y_−7)Rewrite without the parentheses,rearranging to get the like terms together.7y2+4y2__−2y−8y_+9−7Combine like terms.11y2−10y+2
![]() 1
1
Find the sum: (7x2−4x+5)+(x2−7x+3)
- Answer
-
8x2−11x+8
Be careful with the signs as you distribute while subtracting the polynomials in the next example.
Example 3
Find the difference: (9w2−7w+5)−(2w2−4)
Solution
(9w2−7w+5)−(2w2−4)Distribute and identify like terms.9w2__−7w_+5−2w2__+4Rearrange the terms.9w2−2w2__−7w_+5+4Combine like terms.7w2−7w+9
![]() 2
2
Find the difference: (8x2+3x−19)−(7x2−14)
- Answer
-
x2+3x−5
When we add and subtract more than two polynomials, the process is the same. When more than one variable is present, make sure you are combining like terms!
Example 4
Simplify: (a3−a2b)−(ab2+b3)+(a2b+ab2)
Solution
(a3−a2b)−(ab2+b3)+(a2b+ab2)Distributea3−a2b−ab2−b3+a2b+ab2Rearrange the terms to put like terms together.a3−a2b+a2b−ab2+ab2−b3Combine like terms.a3−b3
![]() 3
3
Simplify: (x3−x2y)−(xy2−y3)+(x2y+xy2)
- Answer
-
x3+y3
Multiplying Polynomials
Multiplying a monomial by a monomial
We can use the properties of exponents to multiply monomials.
Example 5
Multiply:
- (3x2)(−4x3)
- (56x3y)(12xy2).
Solution
a.(3x2)(−4x3)Use the Commutative Property of Multiplication to rearrange the factors.3·(−4)·x2·x3Multiply.−12x5
b.(56x3y)(12xy2)Use the Commutative Property of Multiplication to rearrange the factors.56·12·x3·x·y·y2Multiply.10x4y3
![]() 4
4
Multiply:
- (5y7)(−7y4)
- (25a4b3)(15ab3)
- Answer a
-
−35y11
- Answer b
-
6a5b6
Multiplying a polynomial by a monomial
Multiplying a polynomial by a monomial is really just applying the Distributive Property of Multiplication.
Example 6
Multiply:
- −2y(4y2+3y−5)
- 3x3y(x2−8xy+y2).
- Solution a
-
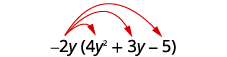
Distribute. 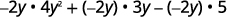
Multiply. 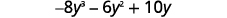
- Solution b
-
3x3y(x2−8xy+y2)Distribute.3x3y⋅x2+(3x3y)⋅(−8xy)+(3x3y)⋅y2Multiply.3x5y−24x4y2+3x3y3
![]() 5
5
Multiply:
- −3y(5y2+8y−7)
- 4x2y2(3x2−5xy+3y2)
- Answer a
-
−15y3−24y2+21y
- Answer b
-
12x4y2−20x3y3+12x2y4
Multiplying a binomial times a binomial
To multiply a binomial by a binomial, we use the Distributive Property of Multiplication twice, and then combine like terms.
Example 7
Multiply:
- (y+5)(y+8)
- (4y+3)(2y−5).
- Solution
-
ⓐ
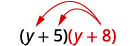
Distribute (y+8). 
Distribute again. 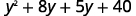
Combine like terms. 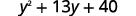
ⓑ
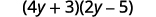
Distribute. 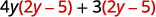
Distribute again. 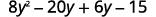
Combine like terms. 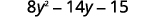
![]() 6
6
Multiply:
- (x+8)(x+9)
- (3c+4)(5c−2)
- Answer a
-
x2+17x+72
- Answer b
-
15c2+14c−8
Patterns
FOIL
If you multiply binomials often enough you may notice a pattern. Notice that the first term in the result is the product of the first terms in each binomial. The second and third terms are the product of multiplying the two outer terms and then the two inner terms. The last term results from multiplying the two last terms in each binomial.
We abbreviate “First, Outer, Inner, Last” as FOIL. The word FOIL is easy to remember and ensures we find all four products. If you are comfortable with the FOIL method, you save yourself one step, as you can see in the following comparison.
Multiply (x+3)(x+7).

NOTE: The FOIL method only applies to multiplying binomials, not other polynomials!
The square of a binomial
When a binomial is squared (multiplied by itself), the result always follows a very particular pattern; namely, the square of the first term added to twice the product of the two terms plus the square of the last term. We refer to the resulting trinomial as a perfect square trinomial. If you know the pattern, you can save yourself one step.
(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2 and(a−b)2=(a−b)(a−b)=a2−ab−ab+(−b)2=a2−2ab+b2
For example,
(2x+7)2=(2x)2+2(2x)(7)+72=4x2+28x+49 and(5y−4)2=(5y)2−2(5y)(4)+42=25y2−40y+16.
Multiplying a binomial by its conjugate
Given a binomial a+b, we refer to the related binomial a−b as its conjugate. Likewise, the conjugate of a−b is a+b. When a binomial is multiplied by its conjugate, we get another pattern, a binomial which is referred to as the difference of squares. Notice that the middle term always adds to zero and drops out; if you know this pattern, you can save yourself one step.
(a+b)(a−b)=a2+ab−ab−b2=a2−b2
For example,
(2x+7)(2x−7)=4x2−49.
Factoring Polynomials
Recall the definition of the greatest common factor (GCF) of two or more expressions, and the "official" way, shown below, to find the GCF. (If you have had a lot of practice with finding a GCF, you may save the "official" rubric for the most difficult cases.)
GREATEST COMMON FACTOR
The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of each of the expressions.
![]() FIND THE GREATEST COMMON FACTOR (GCF) OF TWO EXPRESSIONS.
FIND THE GREATEST COMMON FACTOR (GCF) OF TWO EXPRESSIONS.
- Factor each coefficient into primes. Write all variables with exponents in expanded form.
- List all factors—matching common factors in a column. In each column, circle the common factors.
- Bring down the common factors that all expressions share.
- Multiply the factors.
The next example will show us the steps to find the greatest common factor of three expressions.
Example 8
Find the greatest common factor of 21x3, 9x2, 15x.
- Solution
-
Factor each coefficient into primes and write the
variables with exponents in expanded form.
Circle the common factors in each column.
Bring down the common factors.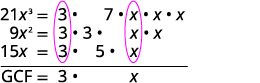
Multiply the factors. 
The GCF of 21x3, 9x2 and 15x is 3x.
![]() 7
7
Find the greatest common factor: 25m4, 35m3, 20m2.
- Answer
-
5m2
Factor the Greatest Common Factor
It is sometimes useful to represent a number as a product of factors; for example, 12 as 2·6 or 3·4. In algebra, it can also be useful to represent a polynomial in factored form. We will start with a polynomial written in standard form, such as 3x2+15x, and rewrite it in factored form as a product, 3x(x+5). To do this we apply the Distributive Property “in reverse.”
Recall the Distributive Property, which we write here once and then again “in reverse," just switching the sides of the equality.
DISTRIBUTIVE PROPERTY
If a, b, and c are real numbers, then
a(b+c)=ab+acandab+ac=a(b+c).
The form on the left is used to multiply. The form on the right is used to factor.
So how do you use the Distributive Property to factor a polynomial? You just find the GCF of all the terms and rewrite the polynomial as a product!
![]() FACTOR THE GREATEST COMMON FACTOR FROM A POLYNOMIAL.
FACTOR THE GREATEST COMMON FACTOR FROM A POLYNOMIAL.
- Find the GCF of all the terms of the polynomial.
- Rewrite each term as a product using the GCF.
- Use the “reverse” Distributive Property to factor the expression.
- Check by multiplying the factors.
FACTOR AS A NOUN AND A VERB
We use “factor” as both a noun and a verb:
Noun:7 is a factor of 14Verb:factor 3 from 3a+3
Example 9
Factor: 5x3−25x2.
- Solution
-
Find the GCF of 5x3 and 25x2. 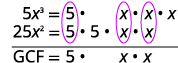
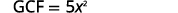
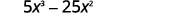
Rewrite each term. 
Factor the GCF. 
Check:
5x2(x−5)5x2·x−5x2·5
5x3−25x2✓
![]() 8
8
Factor: 2x3+12x2.
- Answer
-
2x2(x+6)
When the leading coefficient is negative, factor the negative out as part of the GCF.
Example 10
Factor: −4a3+36a2−8a.
- Solution
-
The leading coefficient is negative, so the GCF will be negative.
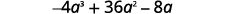
Rewrite each term using the GCF, −4a. 
Factor the GCF. 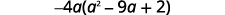
Check:
−4a(a2−9a+2)−4a·a2−(−4a)·9a+(−4a)·2
−4a3+36a2−8a✓
![]() 9
9
Factor: −4b3+16b2−8b.
- Answer
-
−4b(b2−4b+2)
![]() 10
10
Factor: −7a3+28a2−14a.
- Answer
-
−7a(a2−4a+2)
So far our greatest common factors have been monomials. In the next example, the greatest common factor is a binomial.
Example 11
Factor: 3y(y+7)−4(y+7).
- Solution
-
The GCF is the binomial y+7.
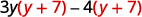
Factor the GCF, (y+7). 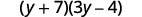
Check on your own by multiplying.
![]() 11
11
Factor: 4m(m+3)−7(m+3).
- Answer
-
(m+3)(4m−7)
![]() 12
12
Factor: 8n(n−4)+5(n−4).
- Answer
-
(n−4)(8n+5)
Factor by Grouping
Factoring by grouping is a technique that enables us to factor polynomials with four terms into a product of binomials. This involves an intermediate step where a common binomial factor will be factored out. For example,
x3−12x2+2x−8=3x3−12x2⏟+2x−8⏟Begin by grouping the first two terms and the last two terms=3x2(x−4)+2(x−4)Factor out the GCF of each grouping A common binomial factor appears=(x−4)(3x2+2)Factor out the common binomial
We can check by multiplying.
(x−4)(3x2+2)=3x3+2x−12x2−8✓
When factoring any polynomial expression, our first step should always be to check for a GCF. Look for the GCF of the coefficients, and then look for the GCF of the variables. Then if there are four terms in the polynomial, try factoring by grouping pairs.
![]() Can every four term polynomial be factored by grouping?
Can every four term polynomial be factored by grouping?
No. Some four term polynomials can be factored by starting with a different pairing of the four terms; however some four term polynomials simply cannot be factored with grouping by pairs. Sometimes four term polynomials can be factored by grouping three terms together first. Some can be factored by determining the possible rational zeros the polynomial might have (see Chapter 3.?). And then, there are some four term polynomials that simply are not factorable. These polynomials are said to be prime.
![]() Given a four term polynomial, factor it
Given a four term polynomial, factor it
- Determine if there are any factors common to all four terms. If so, factor the GCF from each of the four terms.
- Factor the GCF from the first two terms. Factor out the GCF from the last two terms. Sometimes the four terms can be rearranged in order for this to be possible to do.
- If both expressions from step 2 produced the same binomial factor, then factor out this common binomial GCF.
- Check by multiplying the factors.
Example 12: Factor by Grouping
Factor
- 24a4−18a3−20a+15
- xy−2x2y+x3−2y2
Solution
1.24a4−18a3−20a+15=24a4−18a3⏟group - 20a+15⏟group group=6a3(4a−3)+5(−4a+3)Binomial factors are different=6a3(4a−3)−5(4a−3)The binomial factors are the same=(4a−3)(6a3−5)Factor out the common binomial
2.xy−2x2y+x3−2y2=xy−2x2y⏟group + x3−2y2⏟group group=xy(1−2x)+1(x3−2y2)Binomial factors are different=x3−2x2y+xy−2y2change the order of the terms=x3−2x2y⏟group +xy−2y2⏟group group=x2(x−2y)+y(x−2y)The binomial factors are the same=(x−2y)(x2+y)Factor out the common binomial
Analysis. After factoring, we can check our work by multiplying. Use the distributive property to confirm that
24a4−18a3−20a+15=(4a−3)(6a3−5) and xy−2x2y+x3−2y2=(x−2y)(x2+y)
![]() 13
13
Factor x3−x2y−xy+y2
- Answer
- (x−y)(x2−y)
Factoring a Trinomial
There are several techniques we can try when we want to factor a polynomial with three terms. Choosing the right technique may depend on the degree of the polynomial, the value of the leading coefficient, and personal preference.
Factor a Trinomial with Leading Coefficient 1
Although we should always begin by looking for a GCF, pulling out the GCF is not the only way that polynomial expressions can be factored. The polynomial x2+5x+6 has a GCF of 1, but it can be written as the product of the factors (x+2) and (x+3).
To factor a trinomial of the form x2+bx+c, we would like to find two numbers whose product is c and whose sum is b. The trinomial x2+10x+16, for example, can be factored using the numbers 2 and 8 because the product of those numbers is 16 and their sum is 10. The trinomial can be rewritten as the product of (x+2) and (x+8). Here, we are using a Reverse FOIL technique.
FACTORING A SECOND DEGREE TRINOMIAL WITH LEADING COEFFICIENT 1
A trinomial of the form x2+bx+c can be written in factored form as (x+p)(x+q) where pq=c and p+q=b.
 Can every trinomial be factored as a product of binomials?
Can every trinomial be factored as a product of binomials?
No. Some polynomials cannot be factored. These polynomials are said to be prime.
![]() Given a trinomial in the form x2+bx+c, factor it
Given a trinomial in the form x2+bx+c, factor it
- List factor pairs of c.
- Find p and q, a pair of factors of c with a sum of b.
- Write the factored expression (x+p)(x+q).
- Check by multiplying.
Example 13: Factoring a Second Degree Trinomial with Leading Coefficient 1
Factor x2+2x−15.
Solution
We have a trinomial with leading coefficient a=1, b=2, and c=−15. We need to find two numbers with a product of −15 and a sum of 2. In Table 1, we list factor pairs until we find a pair with the desired sum.
| Factors of −15 | Sum of Factors |
|---|---|
| 1,−15 | −14 |
| −1,15 | 14 |
| 3,−5 | −2 |
| −3,5 | 2 |
Now that we have identified p and q as −3 and 5, write the factored form as (x−3)(x+5).
Analysis. We can check our work by multiplying. Use FOIL to confirm that (x−3)(x+5)=x2+2x−15.
 Does the order of the factors matter?
Does the order of the factors matter?
No. Multiplication is commutative, so the order of the factors does not matter. For example, (x−3)(x+5)=(x+5)(x−3).
![]() 14
14
Factor x2−7x+6.
- Answer
-
(x−6)(x−1)
Factor a Second Degree Trinomial with Leading Coefficient Not 1
Trinomials with leading coefficients other than 1 are somewhat more complicated to factor.
Remember to always check for a GCF first! Sometimes, after you factor the GCF, the leading coefficient of the trinomial becomes 1, the degree becomes 2, and you can factor it by the methods we’ve used so far. Let’s do an example to see how this works.
Example 14
Factor completely: 4x3+16x2−20x.
- Solution
-
Is there a greatest common factor?4x3+16x2−20xYes, GCF=4x. Factor it.4x(x2+4x−5)Binomial, trinomial, or more than three terms?It is a trinomial. So “reverse FOIL.”4x(x)(x)Use a table like the one shown to find two numbers that4x(x−1)(x+5)multiply to −5 and add to 4.
Factors of −5 Sum of factors −1,5
1,−5−1+5=4✓
1+(−5)=−4
Check:4x(x−1)(x+5)4x(x2+5x−x−5)4x(x2+4x−5)4x3+16x2−20x✓
![]() 15
15
Factor completely: 5x3+15x2−20x.
- Answer
-
5x(x−1)(x+4)
![]() 16
16
Factor completely: 6y3+18y2−60y.
- Answer
-
6y(y−2)(y+5)
What happens when the leading coefficient is not 1 and there is no GCF? Two different methods for factoring are Reverse FOIL and AC Grouping. The choice of which method to use is largely a matter of personal preference. In some cases, one approach may be more efficient than the other, but this is not really predictable beforehand. The Reverse FOIL Method is illustrated below; the AC grouping method will follow.
Reverse FOIL
Let’s factor the trinomial 3x2+5x+2.
From our earlier work, we expect this will factor into two binomials.
3x2+5x+2()()
We know the first terms of the binomial factors will multiply to give us 3x2. The only reasonable factors of 3x2 are 1x,3x. We can place them in the binomials. Note: Can you see why the factor pair 3,x2 could not possibly work, even though their product is 3x2?

Check: Does 1x·3x=3x2?
We know the last terms of the binomials will multiply to 2. Since this trinomial has all positive terms, we only need to consider positive factors. The only factors of 2 are 1, 2. But we now have two cases to consider as it will make a difference if we write 1, 2 or 2, 1.

Which factors are correct? To decide that, we multiply the inner and outer terms.

Since the middle term of the trinomial is 5x, the factors in the first case will work. Let’s use FOIL to check.
(x+1)(3x+2)3x2+2x+3x+23x2+5x+2✓
![]() Given a trinomial in the form ax2+bx+c, factor by Reverse FOIL.
Given a trinomial in the form ax2+bx+c, factor by Reverse FOIL.
Determine if there are any factors common to all three terms. If so, factor the GCF from each of the three terms. This GCF should be negative if the leading coefficient is negative. Start with ax2+bx+c where any GCF has been factored out.
- Find all the positive factor pairs, S and T, of the leading coefficient a.
Use these pairs to begin constructing possible templates for the final factored result: (Sx)(Tx). - Find all the factor pairs, s and t, of the coefficient c of the last term. Revise the template to look like: (Sxs)(Txt).
If the middle term b is positive and c is positive, the signs of s and t must both be positive.
If the middle term b is negative and c is positive, the signs of s and t must both be negative.
If c is negative, the signs of s and t must be opposites; one must be positive and the other negative. - Determine the signs for s and t so that the sum of the inner and outer products is equal to the coefficient of the middle term: sTx+Stx=bx.
- Check by multiplying.
Example 15
Factor completely using Reverse FOIL: 6b2−13b+5.
- Solution
-
Find the factors of the first term. 
Find the factors of the last term. Consider the signs.
Since the last term, 5, is positive, its factors must both be
positive or both be negative. The coefficient of the
middle term is negative, so we use the negative factors.
Consider all the combinations of factors.
6b2−13b+5 Possible factors Product (b−1)(6b−5) 6b2−11b+5 (b−5)(6b−1) 6b2−31b+5 (2b−1)(3b−5) 6b2−13b+5✓ (2b−5)(3b−1) 6b2−17b+5 The correct factors are those whose productis the original trinomial.(2b−1)(3b−5)Check by multiplying:(2b−1)(3b−5)6b2−10b−3b+56b2−13b+5✓
![]() 17
17
Factor completely using Reverse FOIL: 8x2−13x+3.
- Answer
-
(2x−3)(4x−1)
![]() 18
18
Factor completely using Reverse FOIL: 10y2−37y+7.
- Answer
-
(2y−7)(5y−1)
When we factor an expression, we always look for a greatest common factor first. If the expression does not have a greatest common factor, there cannot be one in its factors either. This may help us eliminate some of the possible factor combinations.
Example 16
Factor completely using Reverse FOIL: 18x2−37xy+15y2.
- Solution
-
The trinomial is already in descending order, and has no common factors. 
Find the factors of the first term. 
Find the factors of the last term. Consider the signs. Since 15 is positive and the coefficient of the middle term is negative, we use the negative factors.

Consider all the combinations of factors.

The correct factors are those whose product isthe original trinomial.(2x−3y)(9x−5y)Check by multiplying:(2x−3y)(9x−5y)18x2−10xy−27xy+15y218x2−37xy+15y2✓
![]() 19
19
Factor completely using Reverse FOIL 18x2−3xy−10y2.
- Answer
-
(3x+2y)(6x−5y)
Example 17
Factor completely using Reverse FOIL: −10y4−55y3−60y2.
- Answer
-

Notice the greatest common factor, so factor it first. 
Factor the trinomial. 
Consider all the combinations.

-
The correct factors are those whose productis the original trinomial. Remember to includethe factor −5y2.−5y2(y+4)(2y+3)Check by multiplying:−5y2(y+4)(2y+3)−5y2(2y2+8y+3y+12)−10y4−55y3−60y2✓
![]() 20
20
Factor completely using Reverse FOIL: 15n3−85n2+100n.
- Answer
-
5n(n−4)(3n−5)
![]() 21
21
Factor completely using Reverse FOIL: 56q3+320q2−96q.
- Answer
-
8q(q+6)(7q−2)
Factor using the AC Grouping Method
The other method for factoring trinomials with leading coefficients other than 1 is the AC Grouping Method. In this method, the middle x term is rewritten as two terms, and then the resulting four term expression is factored by grouping pairs. For example, the trinomial 2x2+5x+3 can be rewritten as 2x2+2x+3x+3. Now we can begin to factor by grouping, obtaining 2x(x+1)+3(x+1). The GCF of (x+1) is pulled out to finally obtain the factored expression (x+1)(2x+3).
![]() Given a trinomial in the form ax2+bx+c, factor by grouping.
Given a trinomial in the form ax2+bx+c, factor by grouping.
- List factor pairs of ac.
- Find p and q, a pair of factors of ac with a sum of b.
- Rewrite the original expression as ax2+px+qx+c.
- Factor the resulting four term expression using factoring by grouping.
Example 18: Factoring a Trinomial by Grouping
Factor 5x2+7x−6 by grouping.
Solution
We have a trinomial with a=5, b=7, and c=−6. First, determine ac=−30. We need to find two numbers with a product of −30 and a sum of 7. In the table below, we list factor pairs until we find a pair with the desired sum.
| Step 1. List Factors of −30 | Step 2. Find factor pair whose sum is 7 |
|---|---|
| 1,−30 | 1+ -30 = −29 ✗ |
| −1,30 | 1- + 30 = 29 ✗ |
| 2,−15 | 2 + -15 = −13 ✗ |
| −2,15 | -2 + 15 = 13 ✗ |
| 3,−10 | 3 + -10 = −7 ✗ |
| −3,10 | -3 + 10 = 7 ✓ |
Step 3. Rewrite 5x2+7x−6 as 5x2−3x+10x−6
Step 4. Factor by grouping.
x(5x−3)+2(5x−3) Factor out the GCF of each part
(5x−3)(x+2) Factor out the GCF of the expression.
Analysis. We can check our work by multiplying. Use FOIL to confirm that (5x−3)(x+2)=5x2+7x−6.
![]() Try It 22
Try It 22
Factor:
a. 2x2+9x+9
|
b. 6x2+x−1
|
Factor a Perfect Square Trinomial
A perfect square trinomial is a trinomial that can be written as the square of a binomial. Recall that when a binomial is squared, the result is the square of the first term added to twice the product of the two terms and the square of the last term.
(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2 and(a−b)2=(a−b)(a−b)=a2−ab−ab+b2=a2−2ab+b2
We can use these equations to factor any perfect square trinomial.
Perfect Square Trinomials
A perfect square trinomial can be written as the square of a binomial:
a2+2ab+b2=(a+b)2
a2−2ab+b2=(a−b)2
![]() Given a perfect square trinomial, factor it into the square of a binomial
Given a perfect square trinomial, factor it into the square of a binomial
- Confirm that the first term a2 and last term b2 are perfect squares.
- Confirm that the middle term is twice the product of ab.
- Write the factored form as (a+b)2 if the middle term is positive and (a−b)2 if the middle term is negative.
Example 19: Factoring a Perfect Square Trinomial
Factor 25x2+20x+4.
Solution
Notice that 25x2 and 4 are perfect squares because 25x2=(5x)2 and 4=22. Check to see if the middle term is twice the product of 5x and 2. The middle term is, indeed, twice the product: 2(5x)(2)=20x. Therefore, the trinomial is a perfect square trinomial and can be written as (5x+2)2.
![]() 23
23
Factor 49x2−14x+1.
- Answer
-
(7x−1)2
Quadratic form
Sometimes a trinomial does not appear to be in the ax2+bx+c form, but it follows a similar pattern, which is known as quadratic form. We can use a technique called factoring by substitution that will make it fit the ax2+bx+c form. It is standard to use u for the substitution.In ax2+bx+c, the middle term has a variable, x, and its square, x2, is the variable part of the first term. Look for this quadratic form pattern as you try to find a substitution.
Example 20
Factor by substitution: x4−4x2−5.
- Solution
-
The variable part of the middle term is x2 and its square, x4, is the variable part of the first term. (We know (x2)2=x4). If we let u=x2, we can put our trinomial in the ax2+bx+c form we need to factor it.

Rewrite the trinomial to prepare for the substitution. 
Let u=x2 and substitute. 
Factor the trinomial. 
Replace u with x2. 
Check:
(x2+1)(x2−5)x4−5x2+x2−5x4−4x2−5✓
![]() 24
24
Factor by substitution: h4+4h2−12.
- Answer
-
(h2−2)(h2+6)
![]() 25
25
Factor by substitution: y4−y2−20.
- Answer
-
(y2+4)(y2−5)
Factor a Difference of Squares
A difference of squares is a binomial consisting of a perfect square subtracted from a perfect square. Recall that when two binomials containing the same terms but opposite signs (conjugates) are multiplied together, the middle terms cancel each other out, and all that is left is a difference of squares. As usual, the order of the two factors does not matter, since multiplication is commutative.
(a−b)(a+b)=a2+ab−ab+b2=a2−b2 and(a+b)(a−b)=a2−ab+ab+b2=a2−b2
Difference of Squares
A difference of squares can be rewritten as the product of two binomial conjugates.
a2−b2=(a−b)(a+b)
![]() Given a difference of squares, factor it into binomials
Given a difference of squares, factor it into binomials
- Confirm that there are only two terms, both are perfect squares, and the second term is being subtracted from the first.
- Write the factored form as (a−b)(a+b).
Example 21: Factoring a Difference of Squares
Factor 9x^2−25.
Solution
Notice that 9x^2 and 25 are perfect squares because 9x^2={(3x)}^2 and 25=5^2, so if the formula is used, a =3x and b = 5 . The polynomial represents a difference of squares and can be rewritten as (3x−5)(3x+5).
![]() \PageIndex{26}
\PageIndex{26}
Factor 81y^2−100.
- Answer
-
(9y−10)(9y+10)
 Is there a formula to factor the sum of squares?
Is there a formula to factor the sum of squares?
No. A sum of squares is prime and cannot be factored if only real numbers are used.
When factoring, always check the resulting factors to see if any can be factored further.
Example \PageIndex{22}
Factor x^4 - 81y^4 completely .
Solution
First, identify what is being squared. To do this, recall the power rule for exponents, (x^{m})^{n}=x^{mn}. Thus, x ^ { 4 } - 81 y ^ { 4 } = \left( \color{Cerulean}{x ^ { 2} } \right) ^ { 2 } - \left(\color{Cerulean}{ 9 y ^ { 2} } \right) ^ { 2 }. Therefore, substitute a=x^{2} and b=9y^{2} into the formula for difference of squares.
x ^ { 4 } - 81 y ^ { 4 } = \left( x ^ { 2 } - 9 y ^ { 2 } \right) \left( x ^ { 2 } + 9 y ^ { 2 } \right)
At this point, notice that the factor (x^{2}−9y^{2}) is itself a difference of squares and thus can be further factored using a=x^{2} and b=3y. The factor (x^{2}+9y^{2}) is prime and cannot be factored using real numbers.
\begin{aligned} x ^ { 4 } - 81 y ^ { 4 } & =\left( x ^ { 2 } - 9 y ^ { 2 } \right) \left( x ^ { 2 } + 9 y ^ { 2 } \right) \\ & = ( x - 3 y )( x + 3 y ) \left( x ^ { 2 } + 9 y ^ { 2 } \right) \end{aligned}
Factor the Sum and Difference of Cubes
Now, we will look at two new special products: the sum and difference of cubes. Although the sum of squares cannot be factored, the sum of cubes can be factored into a binomial and a trinomial. Similarly, the sum of cubes can be factored into a binomial and a trinomial, but with different signs.
Sum and Difference of Cubes
The sum of two cubes can be factored as
a^3+b^3=(a+b)(a^2−ab+b^2) \nonumber
The difference of two cubes can be factored as
a^3−b^3=(a−b)(a^2+ab+b^2) \nonumber
The acronym SOAP can be used to remember the signs when factoring the sum or difference of cubes. The first letter of each word relates to the signs: Same Opposite AlwaysPositive. Consider the following example.
x^3−2^3=(x−2)(x^2+2x+4) \nonumber
The sign of the first 2 is the Same as the sign between x^3−2^3. The sign of the 2x term is Opposite the sign between x^3−2^3. And the sign of the last term, 4, is Always Positive.
![]() Given a sum of cubes or difference of cubes, factor it
Given a sum of cubes or difference of cubes, factor it
- Confirm both terms are cubes, a^3+b^3 or a^3−b^3. Identify a and b.
- For a sum of cubes, write the factored form as (a+b)(a^2−ab+b^2).
For a difference of cubes, write the factored form as (a−b)(a^2+ab+b^2).
Example \PageIndex{23}: Factoring a Sum of Cubes
Factor x^3+512.
Solution
Notice that x^3 and 512 are cubes because 8^3=512, so a = x and b = 8. Rewrite the sum of cubes as (x+8)(x^2−8x+64).
Analysis. After writing the sum of cubes this way, we might think we should check to see if the trinomial portion can be factored further. However, the second degree trinomial portion cannot be factored, so we do not need to check.
![]() \PageIndex{27}
\PageIndex{27}
Factor the sum of cubes: 216a^3+b^3.
- Answer
-
(6a+b)(36a^2−6ab+b^2)
Example \PageIndex{24}: Factoring a Difference of Cubes
Factor 8x^3−125.
Solution
Notice that 8x^3 and 125 are cubes because 8x^3=(2x)^3 and 125=5^3. Write the difference of cubes as (2x−5)(4x^2+10x+25).
Analysis. Just as with the sum of cubes, we will not be able to further factor the second degree trinomial portion.
![]() \PageIndex{28}
\PageIndex{28}
Factor the difference of cubes: 1000x^3−1
- Answer
-
(10x−1)(100x^2+10x+1)
If a binomial is both a difference of squares and a difference of cubes, then first factor it as a difference of squares. This will result in a more complete factorization.
Example \PageIndex{25}
Factor 64 x ^6 - y ^6 completely.
Solution
This binomial is both a difference of squares and a difference of cubes.
\begin{array} { l } { 64 x ^ { 6 } - y ^ { 6 } = \left( \color{Cerulean}{4 x ^ { 2} } \right) ^ { 3 } - \left( \color{Cerulean}{y ^ { 2} } \right) ^ { 3 } \quad\color{Cerulean} \text{ Difference of cubes } } \\ { 64 x ^ { 6 } - y ^ { 6 } = \left( \color{Cerulean}{8 x ^ { 3} } \right) ^ { 2 } - \left( \color{Cerulean}{y ^ { 3} } \right) ^ { 2 } \quad \color{Cerulean} \text{ Difference of squares } } \end{array}
When confronted with a binomial that is a difference of both squares and cubes, as this is, factor using difference of squares first.
\begin{align*} 64 x ^ 6 - y ^ 6 &= ( 8 x ^ 3 ) ^ 2 - (y ^ 3 ) ^ 2 && \qquad \text{Factor first as a difference of squares} \\ &= ( 8 x ^ 3 - y ^ 3 )( 8 x ^ 3 + y ^ 3 ) \\ &= \underbrace{ ( 8 x ^ 3 - y ^ 3 ) }_{ { ( 2x-y)(4x^2+2xy+y^2 ) } } \cdot \underbrace{ ( 8 x ^ 3 + y ^ 3 ) }_{ { ( 2x+y)(4x^2-2xy+y^2 ) } } && \qquad \text{Then factor a sum and difference of cubes} \\ &= ( 2x-y)(4x^2+2xy+y^2 )( 2x+y)(4x^2-2xy+y^2 ) && \\ \nonumber \end{align*}
All four factors are prime and the expression is completely factored.
![]() \PageIndex{29}
\PageIndex{29}
Factor: a ^ { 6 } b ^ { 6 } - 1
- Answer
-
( a b + 1 ) \left( a ^ { 2 } b ^ { 2 } - a b + 1 \right) ( a b - 1 ) \left( a ^ { 2 } b ^ { 2 } + a b + 1 \right)
![]() Challenge
Challenge
Refer to Example 25. You may wonder why we do not get the same result if we factor using a difference of squares first as opposed to using a difference of cubes first. You may be familiar with the unique factorization property of polynomials, even though this is not part of our precalculus curriculum. However, if you factor the polynomial in Example 25 using a difference of cubes first, the result is 64 x ^6 - y ^6 = (2x-y)(2x+y)(16x^4+4x^2+y^4) . (Try it!) Comparing the two different results, what can we conclude?
- Answer
-
16x^4+4x^2+y^4 = (4x^2+2xy+y^2 )(4x^2-2xy+y^2 )\quad The fourth degree trinomial on the left can be factored as a product of the two second trinomials on the right!
Factoring Summary
The following outlines a useful strategy for factoring polynomials.USE A GENERAL STRATEGY FOR FACTORING POLYNOMIALS.
- Is there a greatest common factor?
Factor it out. - Is the polynomial a binomial, trinomial, or are there more than three terms?
If it is a binomial:- Is it a sum?
Of squares? Sums of squares do not factor.
Of cubes? Use the sum of cubes pattern. - Is it a difference?
Of squares? Factor as the product of conjugates.
Of cubes? Use the difference of cubes pattern.
- Is it of the form x^2+bx+c? Reverse FOIL.
- Is it of the form ax^2+bx+c?
If a and c are squares, check if it fits the trinomial square pattern.
Use the Reverse FOIL or “ac” method.
- Use the grouping method.
- Is it a sum?
- Check.
Is it factored completely?
Do the factors multiply back to the original polynomial?
Remember, a polynomial is completely factored if, other than monomials, its factors are prime!
Example \PageIndex{26}
Factor completely: 7x^3−21x^2−70x.
Solution:
\begin{array} {ll} \text{1. Is there a GCF? Yes, }7x. \text{ Factor out the GCF.} & 7x(x^2−3x−10) \\ \text{2. In the parentheses, is a trinomial } & \\ \hspace{5mm}\text{with leading coefficient 1, so “Undo” FOIL.} &7x(x+2)(x−5) \\ \text{3. Is the expression factored completely? Yes. } & \text{Neither binomial can be factored.} \end{array}
\hspace{5mm}\text{Check. } \quad 7x(x+2)(x−5) \text{ = } 7x(x^2−5x+2x−10) \text{ = } 7x(x^2−3x−10) \text{ = } 7x^3−21x^2−70x\,\checkmark
Be careful when you are asked to factor a binomial, as there are several options!
Example \PageIndex{27}
Factor completely: 24y^2−150
Solution:
\begin{array} {ll} \text{1. Is there a GCF? Yes, }6. \text{ Factor out the GCF.} &6(4y^2−25) \\ \text{2. Two terms are in the parentheses.} & \\ \hspace{5mm}\text{The binomial is a difference of squares.} &6((2y)^2−(5)^2) \\ \hspace{5mm}\text{Write as a product of conjugates.} &6(2y−5)(2y+5) \\ \text{3. Is the expression factored completely? Yes.} & \text{Neither binomial can be factored.} \end{array}
\quad \text{Check. } \quad 6(2y−5)(2y+5) \text{ = } 6(4y^2−25) \text{ = } 24y^2−150\,\checkmark
The next example can be factored using several methods. Recognizing the Perfect Square Trinomial pattern will make your work easier.
Example \PageIndex{28}
Factor completely: 4a^2−12ab+9b^2.
Solution:
\begin{array} {ll} \text{1. Is there a GCF? No.} & \\ \text{2. A trinomial with }a\neq 1.\text{ But the first term is a perfect square.} \\ \hspace{5mm}\text{Is the last term a perfect square? Yes.} &(2a)^2−12ab+(3b)^2 \\ \hspace{5mm}\text{Does it fit the pattern, }a^2−2ab+b^2?\text{ Yes. } &(2a)^2 −12ab+ (3b)^2 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(2a)(3b)}{\,}^{\swarrow}\\ \hspace{5mm}\text{Write it as a binomial square.} &(2a−3b)^2 \\ \text{3. Is the expression factored completely? Yes.} & \text{The binomial cannot be factored.} \end{array} \hspace{5mm} \text{Check. } \quad (2a−3b)^2 \text{ = } (2a)^2−2·2a·3b+(3b)^2 \text{ = } 4a^2−12ab+9b^2\,\checkmark
Remember, sums of squares do not factor, but sums of cubes do!
Example \PageIndex{29}
Factor completely 12x^3y^2+75xy^2.
Solution:
\begin{array} {ll} \text{1. Is there a GCF? Yes, }3xy^2. \text{ Factor out the GCF.} & 3xy^2(4x^2+25) \\ \text{2. In the parentheses is a binomial - a sum of squares} & \text{Sums of squares cannot be factored.} \\ \text{3. Is the expression factored completely? Yes. Check. } & 3xy^2(4x^2+25) \text{ = } 12x^3y^2+75xy^2 \,\checkmark \end{array}
When using the sum or difference of cubes pattern, be careful with the signs.
Example \PageIndex{30}
Factor completely: 24x^3+81y^3.
Solution:
\begin{array} {ll} \text{1. Is there a GCF? Yes, }3. \text{ Factor out the GCF.} &3(8x^3+27y^3) \\ \text{2. Two terms are in the parentheses.} & \\ \quad\text{The binomial is a sum of cubes.} &3((2x)^3+(3y)^3) \\ \quad \text{Factor it using the sum of cubes formula.} & 3(2x+3y)((2x)^2 - 2x \cdot 3y +(3y)^2) \\ & 3(2x+3y)(4x^2-6xy+9y^2) \\ \text{3. Is the expression factored completely? Yes.} & \text{Neither binomial nor trinomial can be factored.} \end{array}
\quad \text{Check. } \quad 3(2x+3y)(4x^2-6xy+9y^2)
\hspace{20mm} \ \text{ = } (6x+9y)(4x^2-6xy+9y^2) \text{ = } 24x^3 -36x^2y +54xy^2 +36x^2y - 54xy^2 +81y^3 \text{ = } 24x^3+81y^3 \,\checkmark
Example \PageIndex{31}
Factor completely: 3x^5y−48xy.
Solution:
\begin{array} {ll} \text{1. Is there a GCF? Yes, }3xy. \text{ Factor out the GCF.} &3xy(x^4−16) \\ \text{2. The binomial in parentheses is a difference of squares.} &3xy\left((x^2)^2−(4)^2\right) \\ \quad \text{Factor it as a product of conjugates} &3xy(x^2−4)(x^2+4) \\ \text{3. Is the expression factored completely? NO!} \\ \text{2. The first binomial is a difference of squares.} &3xy\left((x)^2−(2)^2\right)(x^2+4) \\ \quad \text{Factor it as a product of conjugates.} &3xy(x−2)(x+2)(x^2+4) \\ \text{3. Is the expression factored completely? Yes.} \end{array}
\quad \text{Check. } \quad 3xy(x−2)(x+2)(x^2+4) \text{ = } 3xy(x^2−4)(x^2+4) \text{ = } 3xy(x^4−16) \text{ = } 3x^5y−48xy\,\checkmark
Example \PageIndex{32}
Factor completely: 4x^2+8bx−4ax−8ab.
Solution:
\begin{array} {ll} \text{1. Is there a GCF? Yes, } 4 \text{. Factor out the GCF. } &4(x^2+2bx−ax−2ab) \\
\text{2. There are four terms. Factor each pair.} &4 \big( x {\color{Cerulean}{(x+2b)}} −a {\color{Cerulean}{(x+2b)}} \big) \\
\quad \text{Factor out the common binomial GCF} & 4 {\color{Cerulean}{(x+2b)}} (x−a) \\
\text{3. Is the expression factored completely? Yes.} \end{array}
\quad \text{Check. } \quad 4(x+2b)(x−a) \text{ = } (4x + 8b)(x- a) \text{ = } 4x^2−4ax+8bx−8ab \,\checkmark
Example \PageIndex{33}
Factor completely: 40x^2y+44xy−24y.
Solution:
\begin{array} {ll} \text{1. Is there a GCF? Yes, } 4y \text{. Factor out the GCF. } &4y(10x^2+11x−6) \\
\text{2. Factor the trinomial with }a\neq 1. & 4y(5x−2)(2x+3) \\
\quad \text{Use the Reverse FOIL or AC Grouping Method} & \\
\text{3. Is the expression factored completely? Yes.} \end{array}
\quad \text{Check. } \quad 4y(5x−2)(2x+3) \text{ = } 4y(10x^2+11x−6) \text{ = } 40x^2y+44xy−24y \,\checkmark
Radical Expressions
Definition: Square and Square Root of a Number
Square
If n^{2}=m, then m is the square of n.
Square Root
If n^{2}=m, then n is a square root of m.
Notice that both 13^2=169 and (−13)^{2} = 169. Therefore, both 13 and −13 are square roots of 169.
Every positive number has two square roots—one positive and one negative. When we use a radical sign, and write \sqrt{m}, it denotes the positive square root of m. The positive square root is also called the principal square root. If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, -\sqrt{169}=-13.
Because 0^2=0, \sqrt{0}=0. Notice that zero has only one square root.
Definition: Square Root Notation
\sqrt{m} is read "the square root of m."
If n^2=m, then n=\sqrt{m}, for n\geq 0.
Example \PageIndex{34}
Simplify:
- \sqrt{144}
- -\sqrt{289}
Solution:
a. Since 12^{2}=144, \sqrt{144} = 12.
b. Since 17^{2}=289 and the negative is in front of the radical sign, -\sqrt{289} = -17.
![]() \PageIndex{30}
\PageIndex{30}
Simplify:
- -\sqrt{64}
- \sqrt{225}
- Answer
-
- -8
- 15
Can we simplify \sqrt{-49}? Is there a number whose square is -49?
(___ )^{2}=-49
Since any positive number squared is positive and any negative number squared is positive, there is no real number equal to \sqrt{-49}.
So far we have only talked about squares and square roots. Let’s now extend our work to include higher powers and higher roots.
It will be helpful to have a table of the powers of the integers from −5 to 5.
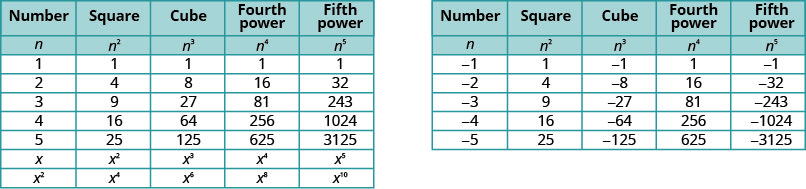
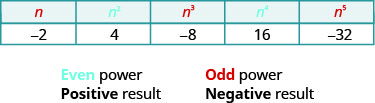
Notice the signs in the table. All powers of positive numbers are positive, of course. But when we have a negative number, the even powers are positive and the odd powers are negative. We’ll copy the row with the powers of −2 to help you see this.
Definition \PageIndex{3}: nth Root of a Number
For any whole number n greater than 1, if b^{n}=a, then b is an n^{th} root of a.
The principal nth root of a is written \sqrt[n]{a} and has the same sign as a.
When a is negative and n is even, the principal nth root is undefined as a real number.
The n is called the index of the radical.
Just as we use the word ‘cubed’ for b^{3}, we use the term ‘cube root’ for \sqrt[3]{a}.
We know that the square root of a negative number is not a real number. The same is true for any even root. Even roots of negative numbers are not real numbers. Odd roots of negative numbers are real numbers.
When n is an even number and
- a \geq 0, then \sqrt[n]{a} is a real number.
- a<0, then \sqrt[n]{a} is not a real number.
When n is an odd number, \sqrt[n]{a} is a real number for all the values of a.
Example \PageIndex{35}
Simplify:
- \sqrt[3]{-125}
- \sqrt[4]{-16}
- \sqrt[5]{-243}
Solution:
a. Since (-5)^{3}=-125, \sqrt[3]{-125} = -5.
b. Think, (?)^{4}=-16. No real number raised to the fourth power is negative. Thus, \sqrt[4]{16} is not a real number.
c. Since (-3)^{5}=-243, \sqrt[5]{-243} = -3.
![]() \PageIndex{31}
\PageIndex{31}
Simplify:
- \sqrt[3]{-27}
- \sqrt[4]{-256}
- \sqrt[5]{-32}
- Answer
-
- -3
- not real
- -2
Estimate and Approximate Roots
When we see a number with a radical sign, we often don’t think about its numerical value. While we probably know that the \sqrt{4}=2, what is the value of \sqrt{21} or \sqrt[3]{50}? In some situations a quick estimate is meaningful and in others it is important to have a decimal approximation.
To get a numerical estimate of a square root, we look for perfect square numbers closest to the radicand (the number inside the radical sign). To find an estimate of \sqrt{11}, we see 11 is between perfect square numbers 9 and 16, closer to 9. Its square root will be between 3 and 4, but closer to 3. Similarly, to estimate \sqrt[3]{91}, we see 91 is between perfect cube numbers 64 and 125. The cube root will be between 4 and 5.
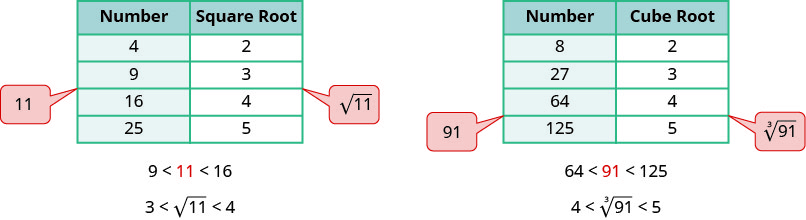
![]() \PageIndex{32}
\PageIndex{32}
Estimate each root between two consecutive whole numbers:
- \sqrt{38}
- \sqrt[3]{200}
- Answer
-
- 6<\sqrt{38}<7
- 5<\sqrt[3]{200}<6
There are mathematical methods to approximate square roots, but nowadays most people use a calculator to find square roots. To find a square root you will use the \sqrt{x} key on your scientific calculator. To find a cube root, or any root with higher index, you will use the \sqrt[y]{x} key.
When you use these keys, you get an approximate value if the radicand is not a perfect square. The approximation is accurate to the number of digits shown on your calculator’s display. The symbol for an approximation is ≈ and it is read ‘approximately’.
Suppose your calculator has a 10 digit display. You would see that
\sqrt{5} \approx 2.236067978, rounded to two decimal places is \sqrt{5} \approx 2.24
\sqrt[4]{93} \approx 3.105422799, rounded to two decimal places is \sqrt[4]{93} \approx 3.11
How do we know these values are approximations and not the exact values? Look at what happens when we square the first and raise the next to the fourth power:
\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}
The squares are close to 5, but are not exactly equal to 5. The fourth powers are close to 93, but not equal to 93. If we had a calculator that displays more digits, could we find the exact value of \sqrt{5} or \sqrt[4]{93}? No, because these are irrational numbers, which have no exact decimal representation, no matter how many digits are displayed.
Note: Most scientific calculators can be programmed to display results rounded to however many decimal places you want (below the maximum).
![]() \PageIndex{33}
\PageIndex{33}
Round to two decimal places:
- \sqrt{11}
- \sqrt[3]{71}
- \sqrt[4]{127}
- Answer
-
- \approx 3.32
- \approx 4.14
- \approx 3.36
Using the Product Rule to Simplify Square Roots
Note: Although we are concerned with simplifying square roots, the following rules and procedures can be modified to apply to any nth root.
"Simplify" a square root means rewrite it so that we can compare and/or combine expressions with square roots. There are several properties of square roots that allow us to simplify complicated radical expressions. The first rule we will look at is the product rule for simplifying square roots, which allows us to separate the square root of a product of two numbers into the product of two separate rational expressions. For instance, we can rewrite \sqrt{15} as \sqrt{3}\times\sqrt{5}. We can also use the product rule to express the product of multiple radical expressions as a single radical expression.
The Product Rule For Simplifying Square Roots
If a and b are nonnegative, the square root of the product ab is equal to the product of the square roots of a and b
\sqrt{ab}=\sqrt{a}\times\sqrt{b}
![]() Simplify the square root of a product
Simplify the square root of a product
- Rewrite the radicand as a product of a perfect square and another factor.
- Write the radical expression as a product of radical expressions.
- Simplify.
Because negative numbers do not have real square roots, assume for the rest of this section that all variables represent nonnegative numbers.
Example \PageIndex{36}: Using the Product Rule to Simplify Square Roots
Simplify the radical expression.
- \sqrt{300}
- \sqrt{162a^5b^4}
Solution
a. \quad \sqrt{300}=\sqrt{100\times3} \quad Rewrite 300 as a product of a perfect square and another factor.
\qquad = \sqrt{100}\times\sqrt{3} \quad Write radical expression as a product of radical expressions.
\qquad = 10 \times \sqrt{3} \quad Simplify by finding the square root of 100.
b. \quad \sqrt{162a^5b^4}=\sqrt{81a^4b^4\times2a} \quad Rewrite radicand as a product of a perfect square and another factor.
\qquad =\sqrt{81a^4b^4}\times\sqrt{2a} \quad Write radical expression as product of radical expressions.
\qquad = 9a^2b^2 \times \sqrt{2a} \quad Simplify.
![]() \PageIndex{34}
\PageIndex{34}
Simplify \sqrt{50x^2y^3z}.
- Answer
-
5xy \times \sqrt{2yz}
Sometimes we are given a product of radical expressions, and want to simplify if possible.
![]() Simplify the product of multiple radical expressions
Simplify the product of multiple radical expressions
- Express the product of multiple radical expressions as a single radical expression.
- Simplify.
Example \PageIndex{5}: Using the Product Rule to Simplify the Product of Multiple Square Roots
Multiply. Simplify the radical expression.
a. \sqrt{12}\times\sqrt{3}
b. \sqrt { 6 x ^ { 3 } y ^ { 3 } } \times \sqrt{2 x^3} .
Solution
a. \quad \text{Express the product as a single radical expression: } \sqrt{12\times3} = \sqrt{36} = 6
b. \quad Begin by writing as a single radical expression: \sqrt { 12 x ^ { 6 } y ^ { 3 } }.
Determine the square factors of 12, x^{ 6} , and y^{ 3}.
\left. \begin{array} { l } { 12 = \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 } \\ { x ^ { 6 } = \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 } }} \\ { y ^ { 3 } = \color{Cerulean}{y ^ { 2} }\color{black}{ \cdot} y } \end{array} \right\} \quad\color{Cerulean}\text{Square factors}
Make these substitutions, and then apply the product rule for radicals and simplify.
\begin{aligned} \sqrt { 12 x ^ { 6 } y ^ { 3 } } & = \sqrt { \color{Cerulean}{2 ^ { 2} }\color{black}{ \cdot} 3 \cdot \color{Cerulean}{\left( x ^ { 3 } \right) ^ { 2 }}\color{black}{ \cdot}\color{Cerulean}{ y ^ { 2} }\color{black}{ \cdot} y } \\ & = \sqrt { 2 ^ { 2 } } \cdot \sqrt { \left( x ^ { 3 } \right) ^ { 2 } } \cdot \sqrt { y ^ { 2 } } \cdot \sqrt { 3 y } \quad\quad\quad\quad\:\color{Cerulean} \text{ Apply the product rule for radicals. } \\ & = 2 \cdot x ^ { 3 } \cdot y \cdot \sqrt { 3 y } \\ & = 2 x ^ { 3 } y \sqrt { 3 y } \quad\color{Cerulean} \text{ Simplify. } \end{aligned}
![]() \PageIndex{5}
\PageIndex{5}
Simplify \sqrt{50x}\times\sqrt{2x}.
- Answer
-
10x
Adding and Subtracting Square Roots
We can combine terms of radical expressions only when they have the same radicand and when they have the same radical type such as square roots. For example, the sum of \sqrt{2} and 3\sqrt{2} is 4\sqrt{2}.
The radical expression \sqrt{2}+\sqrt{18} seemingly cannot be combined since the radicands. However, this is where simplifying radical expressions is valuable. The radical expression \sqrt{18} can be written with a 2 in the radicand, as 3\sqrt{2}, so \sqrt{2}+\sqrt{18}=\sqrt{2}+3\sqrt{2}=4\sqrt{2}.
![]() Simplify a radical expression requiring addition or subtraction of square roots
Simplify a radical expression requiring addition or subtraction of square roots
- Simplify each radical expression.
- Add or subtract expressions with equal radicands.
Often, we will have to simplify before we can identify the like radicals within the terms. If the radicand and the index are not exactly the same, then the radicals are not similar and we cannot combine them.
Example \PageIndex{8}: Add or Subtract Square Roots
Perform the indicated operation and simplify.
- 4 \sqrt { 10 } - 5 \sqrt { 10 }
- 5\sqrt{12}+2\sqrt{3}.
- 20\sqrt{72a^3b^4c}-14\sqrt{8a^3b^4c}
Solution
a. \begin{aligned} \text{ }& \text{ } \\ & \text{ } &4 \sqrt { 10 } - 5 \sqrt { 10 } & = ( 4 - 5 ) \sqrt { 10 } \\ & & &= - 1 \sqrt { 10 } \\ & & &= - \sqrt { 10 } \end{aligned}
b. \quad We can rewrite 5\sqrt{12} as 5\sqrt{4\times3}. According to the product rule, this becomes 5\sqrt{4}\sqrt{3}. The square root of \sqrt{4} is 2 , so the expression becomes 5\times2\sqrt{3}, which is 10\sqrt{3}. Now the terms have the same radicand so we can add.
10\sqrt{3}+2\sqrt{3}=12\sqrt{3} \nonumber
c. \quad Rewrite each term so they have equal radicands.
\begin{align*} 20\sqrt{72a^3b^4c} &= 20\sqrt{9}\sqrt{4}\sqrt{2}\sqrt{a}\sqrt{a^2}\sqrt{(b^2)^2}\sqrt{c}\\ &= 20(3)(2)ab^2\sqrt{2ac}\\ &= 120ab^2\sqrt{2ac} \end{align*}
\begin{align*} 14\sqrt{8a^3b^4c} &= 14\sqrt{2}\sqrt{4}\sqrt{a}\sqrt{a^2}\sqrt{(b^2)^2}\sqrt{c}\\ &= 14(2)ab^2\sqrt{2ac}\\ &= 28|a|b^2\sqrt{2ac} \end{align*}
Now the terms have the same radicand so we can subtract.
120ab^2\sqrt{2ac}-28ab^2\sqrt{2ac}=92ab^2\sqrt{2ac}
![]() \PageIndex{8}
\PageIndex{8}
- Add \sqrt{5}+6\sqrt{20}
- Subtract 3\sqrt{80x}-4\sqrt{45x}
- Answers
-
a. 13\sqrt{5} \qquad b. 0
Example \PageIndex{9}: Adding and Subtracting Square Roots
Simplify.
- 10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 }
- \sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 }
- 2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b }.
Solution
a.
\begin{aligned} & \text{ } && = \color{Cerulean}{10 \sqrt { 5 } - 9 \sqrt { 5 }}\color{black}{ +}\color{OliveGreen}{ 6 \sqrt { 2 } - 7 \sqrt { 2 }} \\ &&& = \sqrt { 5 } - \sqrt { 2 } \end{aligned}
We cannot simplify any further because \sqrt{5} and \sqrt{2} are not like radicals; the radicands are not the same.
\color{YellowOrange}{\text{Caution:}} It is important to point out that \sqrt { 5 } - \sqrt { 2 } \neq \sqrt { 5 - 2 }. We can verify this by calculating the value of each side with a calculator.
\sqrt { 5 } - \sqrt { 2 } \approx 0.82 \qquad \text{ is not the same as } \qquad \sqrt { 5 - 2 } = \sqrt { 3 } \approx 1.73
b.
\begin{aligned} & \text{ } && = \sqrt { 16 \cdot 2 }- \sqrt { 9 \cdot 2 } + \sqrt { 25 \cdot 2 } \\ &&& = 4 \sqrt { 2 } - 3 \sqrt { 2 } + 5 \sqrt { 2 } \\ &&& = 6 \sqrt { 2 } \end{aligned}
At first glance, the radicals do not appear to be similar. However, after simplifying completely, we see that we can combine them.
c. \; Step 1: Simplify the radical expression.
\quad Step 2: Combine all like radicals. Remember to add only the coefficients; the variable parts remain the same.
\begin{array} { l } { 2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b } } \\ { = 2 a \sqrt { 25 \cdot 5 \cdot a ^ { 2 } \cdot b } - a ^ { 2 } \sqrt { 16 \cdot 5 \cdot b } + 4 \sqrt { 4 \cdot 5 \cdot \left( a ^ { 2 } \right) ^ { 2 } b } }\quad\color{Cerulean}{Factor.} \\ { = 2 a \cdot 5 \cdot a \sqrt { 5 b } - a ^ { 2 } \cdot 4 \sqrt { 5 b } + 4 \cdot 2 \cdot a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\:\color{Cerulean}{ Simplify.} \\ { = 10 a ^ { 2 } \sqrt { 5 b } - 4 a ^ { 2 } \sqrt { 5 b } + 8 a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\quad\quad\quad\quad \color{Cerulean}{Combine\:like\:terms.} \\ { = 14 a ^ { 2 } \sqrt { 5 b } } \end{array}
![]() Try It \PageIndex{9}
Try It \PageIndex{9}
Simplify: \sqrt { 20 } + \sqrt { 27 } - 3 \sqrt { 5 } - 2 \sqrt { 12 }.
- Answer
-
- \sqrt { 5 } - \sqrt { 3 }
Caution: Simplifying Radicals
Take careful note of the differences between products and sums within a radical. Assume both x and y are nonnegative.
\begin{array} { l } Products \quad \quad\quad\quad Sums\\\hline { \sqrt { x ^ { 2 } y ^ { 2 } } = x y \quad\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y } \end{array}
The property says that we can simplify radicals when the operation in the radicand is multiplication. There is no corresponding property for addition.
Rationalizing Denominators
An expression involving a square root radical in the denominator is considered to be unsimplified. To simplify, we can remove radicals from the denominators of fractions using a process called rationalizing the denominator.
We know that multiplying by 1 does not change the value of an expression. We use this property of multiplication to change expressions that contain radicals in the denominator. To remove radicals from the denominators of fractions, multiply by the form of 1 that will eliminate the radical.
For a denominator containing a single term, multiply by the radical in the denominator over itself. In other words, if the denominator is b\sqrt{c}, multiply by \dfrac{\sqrt{c}}{\sqrt{c}}.
![]() Given an expression with a single square root radical term in the denominator, rationalize the denominator
Given an expression with a single square root radical term in the denominator, rationalize the denominator
- Multiply the numerator and denominator by the radical in the denominator.
- Simplify.
Sometimes, we will need to continue simplifying by reducing the fraction after rationalizing the denominator.
Example \PageIndex{11}: Rationalize a Denominator Containing a Single Term
Write in simplest form (rationalize the denominator).
| a. \dfrac{2\sqrt{3}}{3\sqrt{10}} | b. \dfrac { \sqrt { 2 } } { \sqrt { 5 x } } | c. \dfrac { 3 a \sqrt { 2 } } { \sqrt { 6 a b } } |
a. The radical in the denominator is \sqrt{10}. So multiply the fraction by \dfrac{\sqrt{10}}{\sqrt{10}}. Then simplify.
\dfrac{2\sqrt{3}}{3\sqrt{10}}\times {\color{Cerulean}{ \dfrac{\sqrt{10}}{\sqrt{10}} } } = \dfrac{2\sqrt{30}}{30} = \dfrac{\sqrt{30}}{15}
b. The goal is to find an equivalent expression without a radical in the denominator. The radicand in the denominator determines the factors that you need to use to rationalize it. In this example, multiply by 1 in the form \frac { \sqrt { 5 x } } { \sqrt { 5 x } }.
\begin{aligned} \frac { \sqrt { 2 } } { \sqrt { 5 x } } & = \frac { \sqrt { 2 } } { \sqrt { 5 x } } \cdot \color{Cerulean}{\frac { \sqrt { 5 x } } { \sqrt { 5 x } } }\\ & = \frac { \sqrt { 10 x } } { \sqrt { 25 x ^ { 2 } } } \quad\quad\: \color{Cerulean} { Simplify. } \\ & = \frac { \sqrt { 10 x } } { 5 x } \end{aligned}
c. In this example, we will multiply by 1 in the form \frac { \sqrt { 6 a b } } { \sqrt { 6 a b } }.
\begin{aligned} \frac { 3 a \sqrt { 2 } } { \sqrt { 6 a b } } & = \frac { 3 a \sqrt { 2 } } { \sqrt { 6 a b } } \cdot \color{Cerulean}{\frac { \sqrt { 6 a b } } { \sqrt { 6 a b } }} \\ & = \frac { 3 a \sqrt { 12 a b } } { \sqrt { 36 a ^ { 2 } b ^ { 2 } } } \quad\quad\color{Cerulean}{Simplify.}\\ & = \frac { 3 a \sqrt { 4 \cdot 3 a b} } { 6 ab } \\ & = \frac { 6 a \sqrt { 3 a b } } { b }\quad\quad\:\:\color{Cerulean}{Cancel.} \\ & = \frac { \sqrt { 3 a b } } { b } \end{aligned}
Notice that b does not cancel in this example. Do not cancel factors inside a radical with those that are outside.
![]() Try It \PageIndex{11}
Try It \PageIndex{11}
Write in simplest form (rationalize the denominator).
| a. \dfrac{12\sqrt{3}}{\sqrt{2}} | b. \sqrt { \dfrac { 9 x } { 2 y } } |
- Answer
-
a. 6\sqrt{6} \qquad b. \frac { 3 \sqrt { 2xy } } { 2 y }

