5.2E: Exercises
- Page ID
- 18831
Verbal
1) Describe the unit circle.
- Answer
-
The unit circle is a circle of radius \(1\) centered at the origin.
2) What do the \(x\)- and \(y\)-coordinates of the points on the unit circle represent?
3) Discuss the difference between a coterminal angle and a reference angle.
- Answer
-
Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, \(t\), formed by the terminal side of the angle \(t\) and the horizontal axis.
4) Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.
5) Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.
- Answer
-
The sine values are equal.
Algebraic
For the exercises 6-9, use the given sign of the sine and cosine functions to find the quadrant in which the terminal point determined by \(t\) lies.
6) \( \sin (t)<0\) and \( \cos (t)<0\)
7) \( \sin (t)>0\) and \( \cos (t)>0\)
- Answer
-
\(\textrm{I}\)
8) \( \sin (t)>0 \) and \( \cos (t)<0\)
9) \( \sin (t)<0 \) and \( \cos (t)>0\)
- Answer
-
\(\textrm{IV}\)
For the exercises 10-22, find the exact value of each trigonometric function.
10) \(\sin \dfrac{π}{2}\)
11) \(\sin \dfrac{π}{3}\)
- Answer
-
\(\dfrac{\sqrt{3}}{2}\)
12) \( \cos \dfrac{π}{2}\)
13) \( \cos \dfrac{π}{3}\)
- Answer
-
\(\dfrac{1}{2}\)
14) \( \sin \dfrac{π}{4}\)
15) \( \cos \dfrac{π}{4}\)
- Answer
-
\(\dfrac{\sqrt{2}}{2}\)
16) \( \sin \dfrac{π}{6}\)
17) \( \sin π\)
- Answer
-
\(0\)
18) \( \sin \dfrac{3π}{2}\)
19) \( \cos π\)
- Answer
-
\(−1\)
20) \( \cos 0\)
21) \(cos \dfrac{π}{6}\)
- Answer
-
\(\dfrac{\sqrt{3}}{2}\)
22) \( \sin 0\)
Numeric
For the exercises 23-33, state the reference angle for the given angle.
23) \(240°\)
- Answer
-
\(60°\)
24) \(−170°\)
25) \(100°\)
- Answer
-
\(80°\)
26) \(−315°\)
27) \(135°\)
- Answer
-
\(45°\)
28) \(\dfrac{5π}{4}\)
29) \(\dfrac{2π}{3}\)
- Answer
-
\(\dfrac{π}{3}\)
30) \(\dfrac{5π}{6}\)
31) \(−\dfrac{11π}{3}\)
- Answer
-
\(\dfrac{π}{3}\)
32) \(\dfrac{−7π}{4}\)
33) \(\dfrac{−π}{8}\)
- Answer
-
\(\dfrac{π}{8}\)
For exercises 34-49, find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not one of the angles on the unit circle, use a calculator and round to three decimal places.
34) \(225°\)
Exercise \(\PageIndex{35}\)
\(300°\)
- Answer
-
\(60°\), Quadrant IV, \( \sin (300°)=−\dfrac{\sqrt{3}}{2}, \cos (300°)=\dfrac{1}{2}\)
36) \(320°\)
37) \(135°\)
- Answer
-
\(45°\), Quadrant II, \( \sin (135°)=\dfrac{\sqrt{2}}{2}, \cos (135°)=−\dfrac{\sqrt{2}}{2}\)
38) \(210°\)
39) \(120°\)
- Answer
-
\(60°\), Quadrant II, \(\sin (120°)=\dfrac{\sqrt{3}}{2}\), \(\cos (120°)=−\dfrac{1}{2}\)
40) \(250°\)
41) \(150°\)
- Answer
-
\(30°\), Quadrant II, \( \sin (150°)=\frac{1}{2}\), \(\cos(150°)=−\dfrac{\sqrt{3}}{2}\)
42) \(\dfrac{5π}{4}\)
Exercise \(\PageIndex{43}\)
\(\dfrac{7π}{6}\)
- Answer
-
\(\dfrac{π}{6}\), Quadrant III, \(\sin \left( \dfrac{7π}{6}\right )=−\dfrac{1}{2}\), \(\cos \left (\dfrac{7π}{6} \right)=−\dfrac{\sqrt{3}}{2}\)
44) \(\dfrac{5π}{3}\)
45) \(\dfrac{3π}{4}\)
- Answer
-
\(\dfrac{π}{4}\), Quadrant II, \(\sin \left(\dfrac{3π}{4}\right)=\dfrac{\sqrt{2}}{2}\), \(\cos\left(\dfrac{4π}{3}\right)=−\dfrac{\sqrt{2}}{2}\)
46) \(\dfrac{4π}{3}\)
47) \(\dfrac{2π}{3}\)
- Answer
-
\(\dfrac{π}{3}\), Quadrant II, \( \sin \left(\dfrac{2π}{3}\right)=\dfrac{\sqrt{3}}{2}\), \( \cos \left(\dfrac{2π}{3}\right)=−\dfrac{1}{2}\)
48) \(\dfrac{5π}{6}\)
49) \(\dfrac{7π}{4}\)
- Answer
-
\(\dfrac{π}{4}\), Quadrant IV, \( \sin \left(\dfrac{7π}{4}\right)=-\dfrac{\sqrt{2}}{2}\), \( \cos \left(\dfrac{7π}{4}\right)=\dfrac{\sqrt{2}}{2}\)
50) If \(\cos (t)=\dfrac{1}{7}\) and \(t\) is in the \(4^{th}\) quadrant, find \( \sin (t)\).
51) If \( \cos (t)=\dfrac{2}{9}\) and \(t\) is in the \(1^{st}\) quadrant, find \(\sin (t)\).
- Answer
-
\(\dfrac{\sqrt{77}}{9}\)
52) If \(\sin (t)=\dfrac{3}{8}\) and \(t\) is in the \(2^{nd}\) quadrant, find \( \cos (t)\).
Exercise \(\PageIndex{53}\)
If \( \sin (t)=−\dfrac{1}{4}\) and \(t\) is in Quadrant III, find \(\cos (t)\).
- Answer
-
\(−\dfrac{\sqrt{15}}{4}\)
55) Find the coordinates of the point on a circle with radius \(20\) corresponding to an angle of \(120°\).
- Answer
-
\((−10,10\sqrt{3})\)
56) Find the coordinates of the point on a circle with radius \(8\) corresponding to an angle of \(\dfrac{7π}{4}\).
57) Find the coordinates of the point on a circle with radius \(16\) corresponding to an angle of \(\dfrac{5π}{9}\).
- Answer
-
\((–2.778,15.757)\)
58) State the domain of the sine and cosine functions.
59) State the range of the sine and cosine functions.
- Answer
-
\([–1,1]\)
Graphical
For the exercises 60-79, use the given point on the unit circle to find the value of the sine and cosine of \(t\).
60)
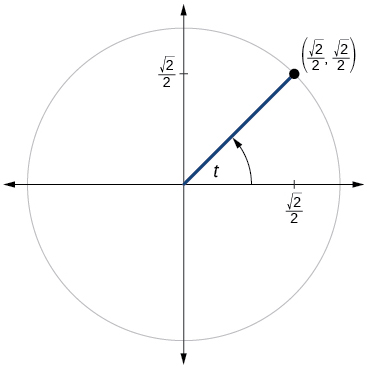
61)
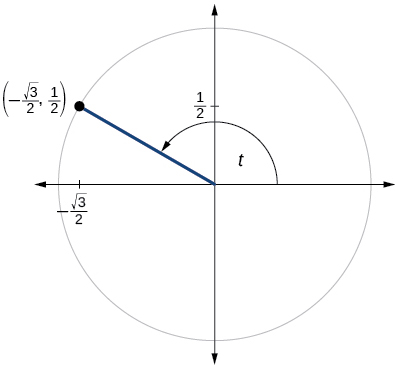
- Answer
-
\( \sin t=\dfrac{1}{2}, \cos t=−\dfrac{\sqrt{3}}{2}\)
62)
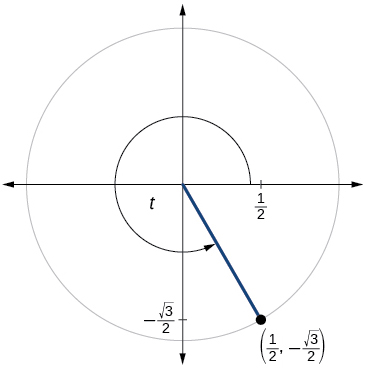
63)
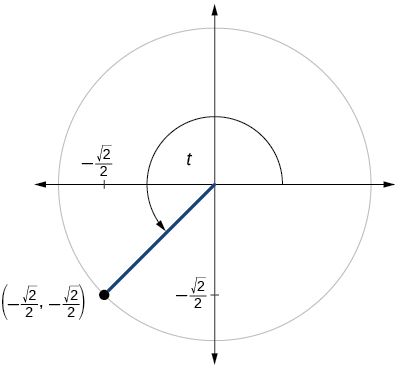
- Answer
-
\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=−\dfrac{\sqrt{2}}{2}\)
64)
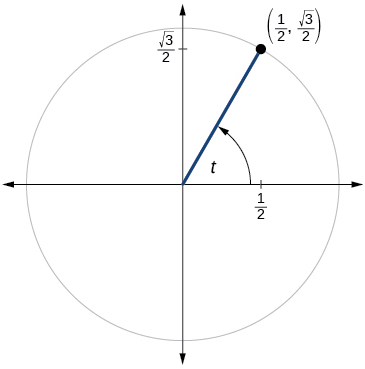
65)
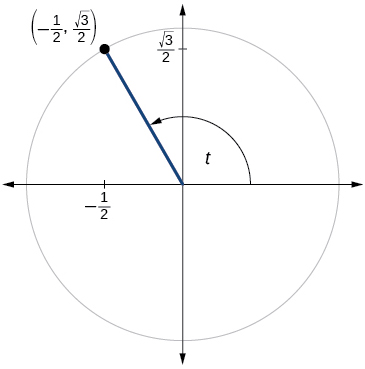
- Answer
-
\( \sin t=\dfrac{\sqrt{3}}{2},\cos t=−\dfrac{1}{2}\)
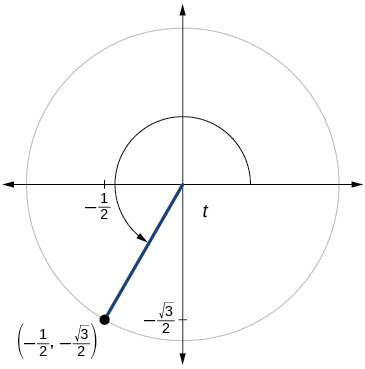
66)
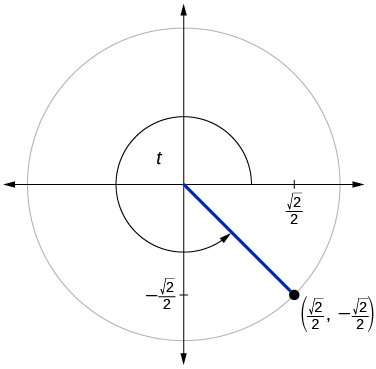
67)
- Answer
-
\( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=\dfrac{\sqrt{2}}{2}\)
68)
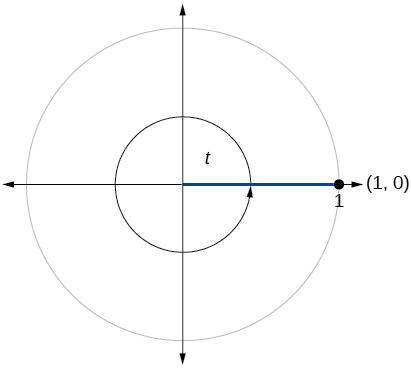
69)
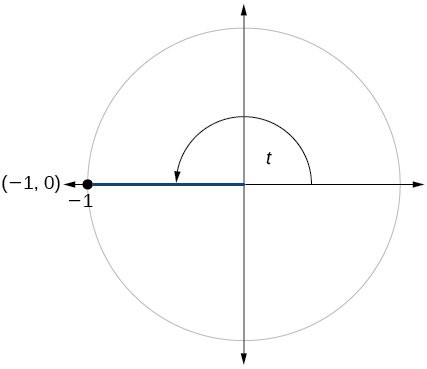
- Answer
-
\( \sin t=0, \cos t=−1\)
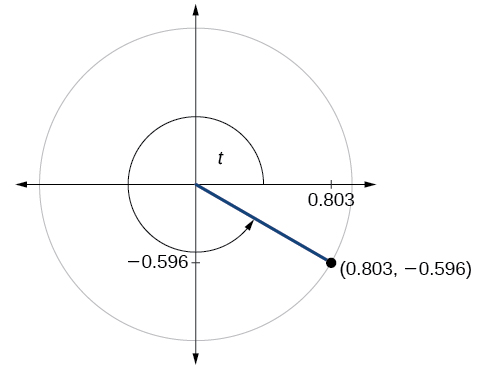
70)
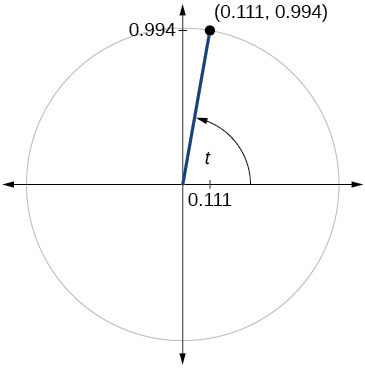
71)
- Answer
-
\( \sin t=−0.596, \cos t=0.803\)
72)
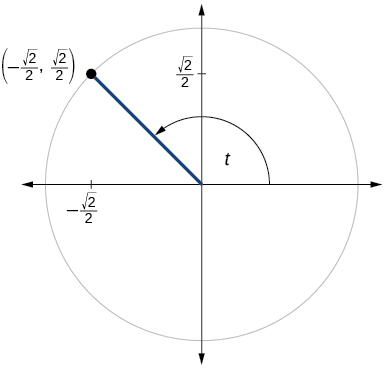
73)
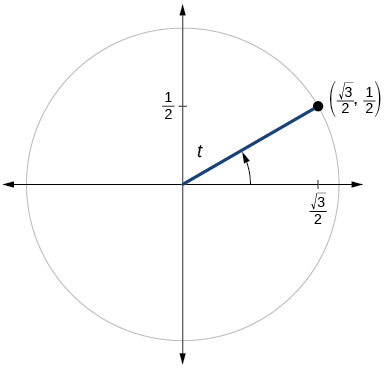
- Answer
-
\(\sin t=\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2}\)
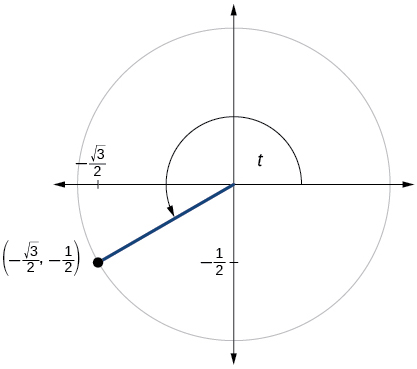
74)
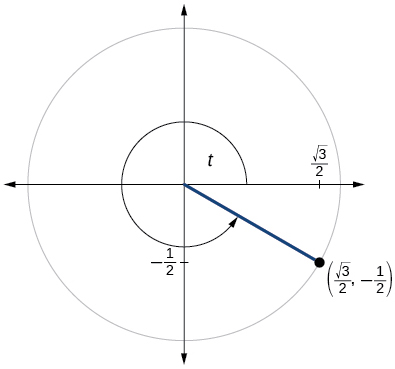
75)
- Answer
-
\( \sin t=−\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2} \)
76)
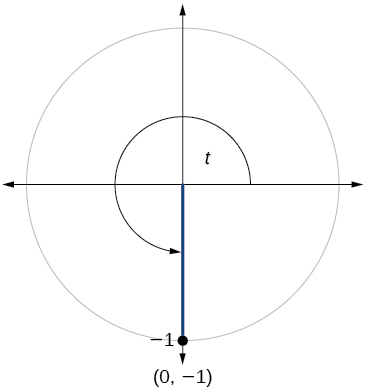
77)
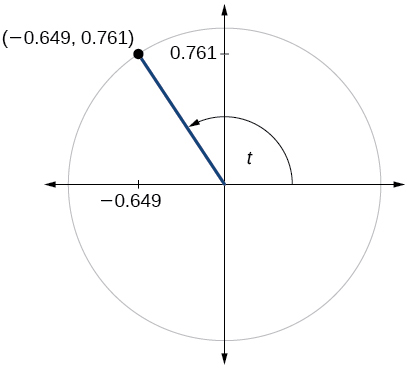
- Answer
-
\( \sin t=0.761, \cos t=−0.649 \)
78)
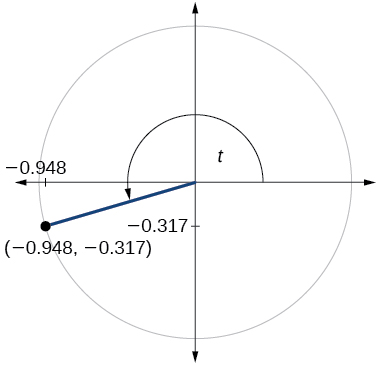
79)
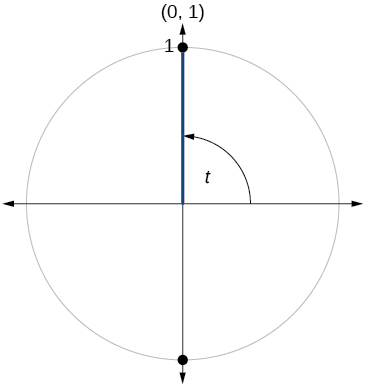
- Answer
-
\( \sin t=1, \cos t=0\)
Technology
For the exercises 80-89, use a graphing calculator to evaluate.
80) \( \sin \dfrac{5π}{9}\)
81) \(cos \dfrac{5π}{9}\)
- Answer
-
\(−0.1736\)
82) \( \sin \dfrac{π}{10}\)
83) \( \cos \dfrac{π}{10}\)
- Answer
-
\(0.9511\)
84) \( \sin \dfrac{3π}{4}\)
85) \(\cos \dfrac{3π}{4}\)
- Answer
-
\(−0.7071\)
86) \( \sin 98° \)
87) \( \cos 98° \)
- Answer
-
\(−0.1392\)
88) \( \cos 310° \)
89) \( \sin 310° \)
- Answer
-
\(−0.7660\)
Extensions
For the exercises 90-99, evaluate.
90) \( \sin \left(\dfrac{11π}{3}\right) \cos \left(\dfrac{−5π}{6}\right)\)
91) \( \sin \left(\dfrac{3π}{4}\right) \cos \left(\dfrac{5π}{3}\right) \)
- Answer
-
\(\dfrac{\sqrt{2}}{4}\)
92) \( \sin \left(− \dfrac{4π}{3}\right) \cos \left(\dfrac{π}{2}\right)\)
93) \( \sin \left(\dfrac{−9π}{4}\right) \cos \left(\dfrac{−π}{6}\right)\)
- Answer
-
\(−\dfrac{\sqrt{6}}{4}\)
94) \( \sin \left(\dfrac{π}{6}\right) \cos \left(\dfrac{−π}{3}\right) \)
95) \( \sin \left(\dfrac{7π}{4}\right) \cos \left(\dfrac{−2π}{3}\right) \)
- Answer
-
\(\dfrac{\sqrt{2}}{4}\)
96) \( \cos \left(\dfrac{5π}{6}\right) \cos \left(\dfrac{2π}{3}\right)\)
97) \( \cos \left(\dfrac{−π}{3}\right) \cos \left(\dfrac{π}{4}\right) \)
- Answer
-
\(\dfrac{\sqrt{2}}{4}\)
98) \( \sin \left(\dfrac{−5π}{4}\right) \sin \left(\dfrac{11π}{6}\right)\)
99) \( \sin (π) \sin \left(\dfrac{π}{6}\right) \)
- Answer
-
\(0\)
Real-World Applications
For the exercises 100-104, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point \((0,1)\), that is, on the due north position. Assume the carousel revolves counter clockwise.
100) What are the coordinates of the child after \(45\) seconds?
101) What are the coordinates of the child after \(90\) seconds?
- Answer
-
\((0,–1)\)
102) What is the coordinates of the child after \(125\) seconds?
103) When will the child have coordinates \((0.707,–0.707)\) if the ride lasts \(6\) minutes? (There are multiple answers.)
- Answer
-
\(37.5\) seconds, \(97.5\) seconds, \(157.5\) seconds, \(217.5\) seconds, \(277.5\) seconds, \(337.5\) seconds
104) When will the child have coordinates \((−0.866,−0.5)\) if the ride last \(6\) minutes?