7.2E: Exercises

Verbal

1) Explain the basis for the cofunction identities and when they apply.

Answer

The cofunction identities apply to complementary angles. Viewing the two acute angles of a right triangle, if one of those angles measures $x$$,$ the second angle measures $\dfrac{\pi }{2}-x$$.$Then $\sin x=\cos \left (\dfrac{\pi }{2}-x \right )$$.$The same holds for the other cofunction identities. The key is that the angles are complementary.

2) Is there only one way to evaluate $\cos \left (\dfrac{5\pi }{4} \right )$$?$Explain how to set up the solution in two different ways, and then compute to make sure they give the same answer.

3) Explain to someone who has forgotten the even-odd properties of sinusoidal functions how the addition and subtraction formulas can determine this characteristic for $f(x)=\sin (x)$ and $g(x)=\cos (x)$$.$(Hint: $0-x=-x$)

Answer

$\sin (-x)=-\sin x$, so $\sin x$ is odd. $\cos (-x)=\cos (0-x)=\cos x$, so $\cos x$ is even.

Algebraic

For exercises 4-9, find the exact value.

4) $\cos \left (\dfrac{7\pi }{12} \right)$

5) $\cos \left (\dfrac{\pi }{12} \right)$

Answer

$\dfrac{\sqrt{2}+\sqrt{6}}{4}$

6) $\sin \left (\dfrac{5\pi }{12} \right)$

7) $\sin \left (\dfrac{11\pi }{12} \right)$

Answer

$\dfrac{\sqrt{6}-\sqrt{2}}{4}$

8) $\tan \left (-\dfrac{\pi }{12} \right)$

9) $\tan \left (\dfrac{19\pi }{12} \right)$

Answer

$-2-\sqrt{3}$

For exercises 10-13, rewrite in terms of $\sin x$ and $\cos x$

10) $\sin \left (x+\dfrac{11\pi }{6} \right)$

11) $\sin \left (x-\dfrac{3\pi }{4} \right)$

Answer

$-\dfrac{\sqrt{2}}{2}\sin x-\dfrac{\sqrt{2}}{2}\cos x$

12) $\cos \left (x-\dfrac{5\pi }{6} \right)$

13) $\cos \left (x+\dfrac{2\pi }{3} \right)$

Answer

$-\dfrac{1}{2}\cos x-\dfrac{\sqrt{3}}{2}\sin x$

For exercises 14-19, simplify the given expression.

14) $\csc \left (\dfrac{\pi }{2}-t \right)$

15) $\sec \left (\dfrac{\pi }{2}-\theta \right)$

Answer

$\csc \theta$

16) $\cot \left (\dfrac{\pi }{2}-x \right)$

17) $\tan \left (\dfrac{\pi }{2}-x \right)$

Answer

$\cot x$

18) $\sin(2x)\cos(5x)-\sin(5x)\cos(2x)$

19) $\dfrac{\tan \left (\dfrac{3}{2}x \right)-\tan \left (\dfrac{7}{5}x \right)}{1+\tan \left (\dfrac{3}{2}x \right)\tan \left (\dfrac{7}{5}x \right)}$

Answer

$\tan \left (\dfrac{x}{10} \right)$

For exercises 20-21, find the requested information.

20) Given that $\sin a=\dfrac{2}{3}$ and $\cos b=-\dfrac{1}{4}$$,$ with $a$ and $b$ both in the interval $\left [ \dfrac{\pi }{2}, \pi \right )$$,$ find $\sin (a+b)$ and $\cos (a-b)$.

21) Given that $\sin a=\dfrac{4}{5}$ and $\cos b=\dfrac{1}{3}$ , with $a$ and $b$ both in the interval $\left [ 0, \dfrac{\pi }{2} \right )$ , find $\sin (a-b)$ and $\cos (a+b)$.

Answer

$\sin (a-b)=\left ( \dfrac{4}{5} \right )\left ( \dfrac{1}{3} \right )-\left ( \dfrac{3}{5} \right )\left ( \dfrac{2\sqrt{2}}{3} \right )=\dfrac{4-6\sqrt{2}}{15}$

$\cos (a+b)=\left ( \dfrac{3}{5} \right )\left ( \dfrac{1}{3} \right )-\left ( \dfrac{4}{5} \right )\left ( \dfrac{2\sqrt{2}}{3} \right )=\dfrac{3-8\sqrt{2}}{15}$

For exercises 22-24, find the exact value of each expression.

22) $\sin \left ( \cos^{-1}\left ( 0 \right )- \cos^{-1}\left ( \dfrac{1}{2} \right )\right )$

23) $\cos \left ( \cos^{-1}\left ( \dfrac{\sqrt{2}}{2} \right )+ \sin^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )\right )$

Answer

$\dfrac{\sqrt{2}-\sqrt{6}}{4}$

24) $\tan \left ( \sin^{-1}\left ( \dfrac{1}{2} \right )- \cos^{-1}\left ( \dfrac{1}{2} \right )\right )$

Graphical

For exercises 25-32, simplify the expression, and then graph both expressions as functions to verify the graphs are identical.

25) $\cos \left ( \dfrac{\pi }{2}-x \right )$

Answer

$\sin x$

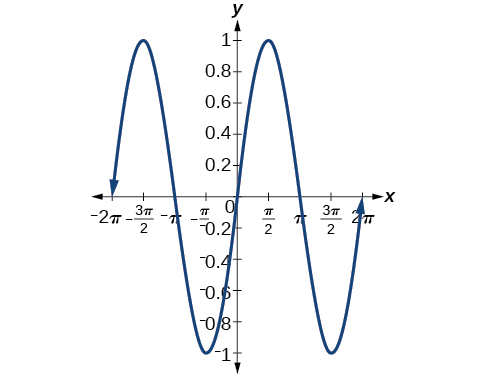
26) $\sin (\pi -x)$

27) $\tan \left ( \dfrac{\pi }{3}+x \right )$

Answer

$\cot \left ( \dfrac{\pi }{6}-x \right )$

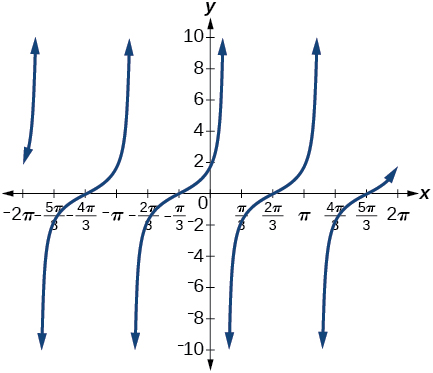
28) $\sin \left ( \dfrac{\pi }{3}+x \right )$

29) $\tan \left ( \dfrac{\pi }{4}-x \right )$

Answer

$\cot \left ( \dfrac{\pi }{4}+x \right )$

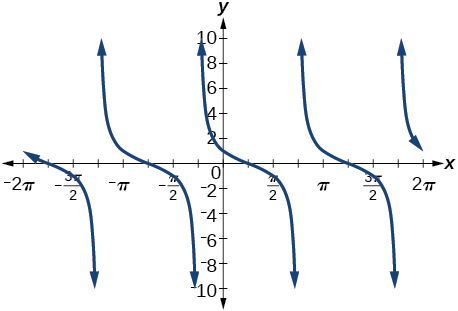
30) $\cos \left ( \dfrac{7\pi }{6}+x \right )$

31) $\sin \left ( \dfrac{\pi }{4}+x \right )$

Answer

$\dfrac{\sin x}{\sqrt{2}}+\dfrac{\cos x}{\sqrt{2}}$

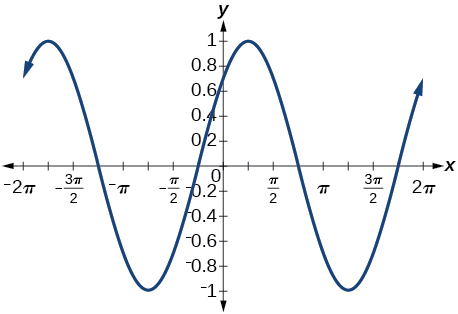
32) $\cos \left ( \dfrac{5\pi }{4}+x \right )$

For exercises 33-41, use a graph to determine whether the functions are the same or different. If they are the same, show why. If they are different, replace the second function with one that is identical to the first. (Hint: think $2x=x+x$)

33) $f(x)=\sin(4x)-\sin(3x)\cos x, g(x)=\sin x \cos(3x)$

Answer

They are the same.

34) $f(x)=\cos(4x)+\sin x \sin(3x), g(x)=-\cos x \cos(3x)$

35) $f(x)=\sin(3x)\cos(6x), g(x)=-\sin(3x)\cos(6x)$

Answer

They are different, try $g(x)=\sin(9x)-\cos(3x)\sin(6x)$

36) $f(x)=\sin(4x), g(x)=\sin(5x)\cos x-\cos(5x)\sin x$

37) $f(x)=\sin(2x), g(x)=2 \sin x \cos x$

Answer

They are the same.

38) $f(\theta )=\cos(2\theta ), g(\theta )=\cos^2\theta -\sin^2\theta$

39) $f(\theta )=\tan(2\theta ), g(\theta )=\dfrac{\tan \theta }{1+\tan^2\theta }$

Answer

They are different, try $g(\theta )=\dfrac{2\tan \theta }{1-\tan^2\theta }$

40) $f(x)=\sin(3x)\sin x, g(x)=\sin^2(2x)\cos^2x-\cos^2(2x)\sin2x$

41) $f(x)=\tan(-x), g(x)=\dfrac{\tan x-\tan(2x)}{1-\tan x \tan(2x)}$

Answer

They are different, try $g(x)=\dfrac{\tan x-\tan(2x)}{1+\tan x \tan(2x)}$

Technology

For the exercises 42-46, find the exact value algebraically, and then confirm the answer with a calculator to the fourth decimal point.

42) $\sin (75^{\circ})$

43) $\sin (195^{\circ})$

Answer

$-\dfrac{\sqrt{3}-1}{2\sqrt{2}}$, or $-0.2588$

44) $\cos (165^{\circ})$

45) $\cos (345^{\circ})$

Answer

$\dfrac{1+\sqrt{3}}{2\sqrt{2}}$, or $-0.9659$

46) $\tan (-15^{\circ})$

Extensions

For the exercises 47-51, prove the identities provided.

47) $\tan \left ( x+\dfrac{\pi }{4} \right )=\dfrac{\tan x+1}{1-\tan x}$

Answer

$\begin{align*} \tan \left ( x+\dfrac{\pi }{4} \right ) &= \\ \dfrac{\tan x + \tan\left (\tfrac{\pi}{4} \right )}{1-\tan x \tan\left (\tfrac{\pi}{4} \right )} &= \\ \dfrac{\tan x+1}{1-\tan x(1)} &= \dfrac{\tan x+1}{1-\tan x} \end{align*}$

48) $\dfrac{\tan (a+b)}{\tan (a-b)}=\dfrac{\sin a \cos a + \sin b \cos b}{\sin a \cos a - \sin b \cos b}$

49) $\dfrac{\cos (a+b)}{\cos a \cos b}=1-\tan a \tan b$

Answer

$\begin{align*} \dfrac{\cos (a+b)}{\cos a \cos b} &= \\ \dfrac{\cos a \cos b}{\cos a \cos b}- \dfrac{\sin a \sin b}{\cos a \cos b} &= 1-\tan a \tan b \end{align*}$

50) $\cos(x+y)\cos(x-y)=\cos^2x-\sin^2y$

51) $\dfrac{\cos(x+h)-\cos(x)}{h}=\cos x\dfrac{\cos h-1}{h}-\sin x \dfrac{\sin h}{h}$

Answer

$\begin{align*} \dfrac{\cos(x+h)-\cos(x)}{h} &= \\ \dfrac{\cos x\cosh - \sin x\sinh -\cos x}{h} &= \\ \dfrac{\cos x(\cosh-1) - \sin x(\sinh-1)}{h} &= \cos x\dfrac{\cos h-1}{h}-\sin x \dfrac{\sin h}{h} \end{align*}$

For the exercises 52-, prove or disprove the statements.

52) $\tan (u+v)=\dfrac{\tan u+\tan v}{1-\tan u \tan v}$

53) $\tan (u-v)=\dfrac{\tan u-\tan v}{1+\tan u \tan v}$

Answer

True

54) $\dfrac{\tan (x+y)}{1+\tan x \tan x}=\dfrac{\tan x + \tan y}{1-\tan^2 x \tan^2 y}$

55) If $\alpha ,\beta$$,$ and $\gamma$ are angles in the same triangle, then prove or disprove $\sin(α+β)=\sin γ$.

Answer

True. Note that $\sin (\alpha +\beta )=\sin (\pi -\gamma )$ and expand the right hand side.

56) If $\alpha ,\beta$ , and $\gamma$ are angles in the same triangle, then prove or disprove $\tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \tan \beta \tan \gamma$.