11.1: The Standard Normal Probability Distribution
- Last updated
- Aug 12, 2022
- Save as PDF
- Page ID
- 109921
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Identify the characteristics of a normal distribution.
- Identify and use the Empirical Rule (68-95-99.7 Rule) for normal distributions.
- Calculate a z-score and relate it to probability.
- Determine if a data set corresponds to a normal distribution.
The Characteristics of a Normal Distribution
Shape
When graphing the data from each of the examples in the introduction, the distributions from each of these situations would be mound-shaped and mostly symmetric. A normal distribution is a perfectly symmetric, mound-shaped distribution. It is commonly referred to the as a normal curve, or bell curve.
Because so many real data sets closely approximate a normal distribution, we can use the idealized normal curve to learn a great deal about such data. With a practical data collection, the distribution will never be exactly symmetric, so just like situations involving probability, a true normal distribution only results from an infinite collection of data. Also, it is important to note that the normal distribution describes a continuous random variable.
Center
Due to the exact symmetry of a normal curve, the center of a normal distribution, or a data set that approximates a normal distribution, is located at the highest point of the distribution, and all the statistical measures of center we have already studied (the mean, median, and mode) are equal.

It is also important to realize that this center peak divides the data into two equal parts.
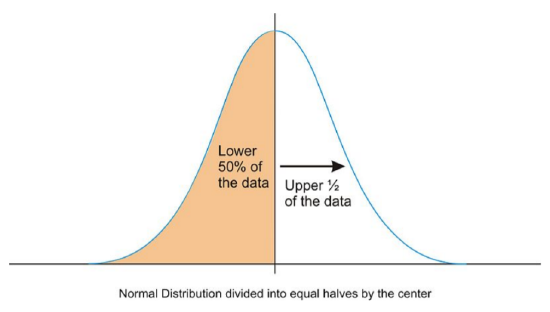
Spread
Let’s go back to our popcorn example. The bag advertises a certain time, beyond which you risk burning the popcorn. From experience, the manufacturers know when most of the popcorn will stop popping, but there is still a chance that there are those rare kernels that will require more (or less) time to pop than the time advertised by the manufacturer. The directions usually tell you to stop when the time between popping is a few seconds, but aren’t you tempted to keep going so you don’t end up with a bag full of un-popped kernels? Because this is a real, and not theoretical, situation, there will be a time when the popcorn will stop popping and start burning, but there is always a chance, no matter how small, that one more kernel will pop if you keep the microwave going. In an idealized normal distribution of a continuous random variable, the distribution continues infinitely in both directions.
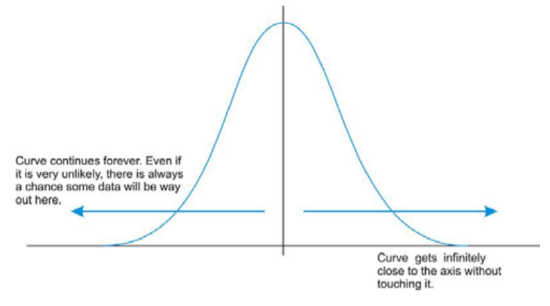
Because of this infinite spread, the range would not be a useful statistical measure of spread. The most common way to measure the spread of a normal distribution is with the standard deviation, or the typical distance away from the mean. Because of the symmetry of a normal distribution, the standard deviation indicates how far away from the maximum peak the data will be. Here are two normal distributions with the same center (mean):
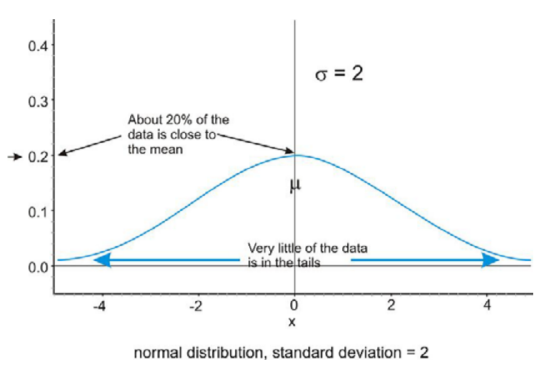
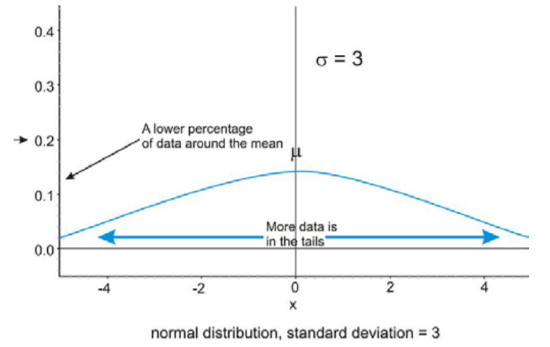
The first distribution pictured above has a smaller standard deviation, and so more of the data are heavily concentrated around the mean than in the second distribution. Also, in the first distribution, there are fewer data values at the extremes than in the second distribution. Because the second distribution has a larger standard deviation, the data are spread farther from the mean value, with more of the data appearing in the tails.
Technology Note: Investigating the Normal Distribution on a TI-83/84 Graphing Calculator
We can graph a normal curve for a probability distribution on the TI-83/84 calculator. To do so, first press [Y=]. To create a normal distribution, we will draw an idealized curve using something called a density function. The command is called ‘normalpdf(’, and it is found by pressing [2nd][DISTR][1]. Enter an X to represent the random variable, followed by the mean and the standard deviation, all separated by commas. For this example, choose a mean of 5 and a standard deviation of 1.
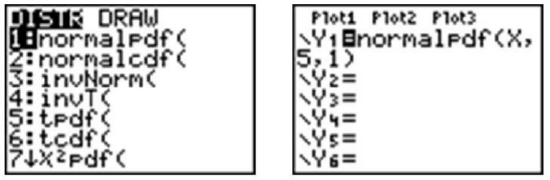
Adjust your window to match the following settings and press [GRAPH].

Press [2ND][QUIT] to go to the home screen. We can draw a vertical line at the mean to show it is in the center of the distribution by pressing [2ND][DRAW] and choosing ‘Vertical’. Enter the mean, which is 5, and press [ENTER].
Remember that even though the graph appears to touch the x-axis, it is actually just very close to it.
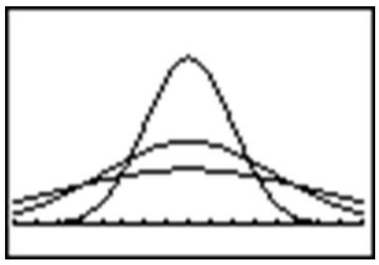
In your Y= Menu, enter the following to graph 3 different normal distributions, each with a different standard deviation:

This makes it easy to see the change in spread when the standard deviation changes.
The Empirical Rule for Normal Distributions
Because of the similar shape of all normal distributions, we can measure the percentage of data that is a certain distance from the mean no matter what the standard deviation of the data set is. The following graph shows a normal distribution with µ=0 and σ=1. This curve is called a standard normal curve. In this case, the values of x represent the number of standard deviations away from the mean.
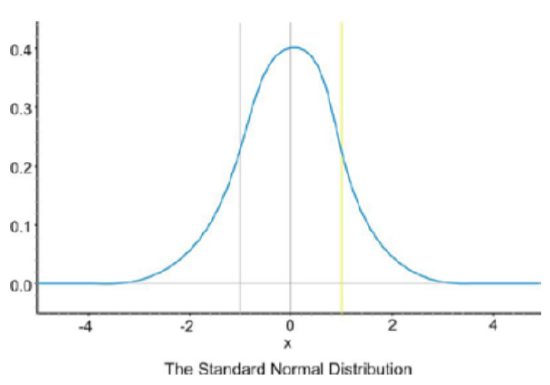
Notice that vertical lines are drawn at points that are exactly one standard deviation to the left and right of the mean. We have consistently described standard deviation as a measure of the typical distance away from the mean. How much of the data is actually within one standard deviation of the mean? To answer this question, think about the space, or area, under the curve. The entire data set, or 100% of it, is contained under the whole curve. What percentage would you estimate is between the two lines? To help estimate the answer, we can use a graphing calculator. Graph a standard normal distribution over an appropriate window.
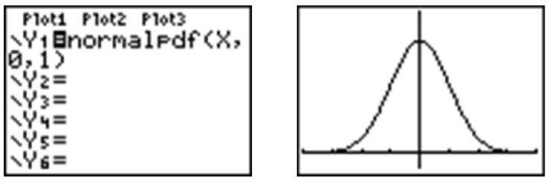
Now press [2ND][DISTR], go to the DRAW menu, and choose ‘ShadeNorm(’. Insert ‘−1, 1’ after the ‘Shade-Norm(’ command and press [ENTER]. It will shade the area within one standard deviation of the mean.
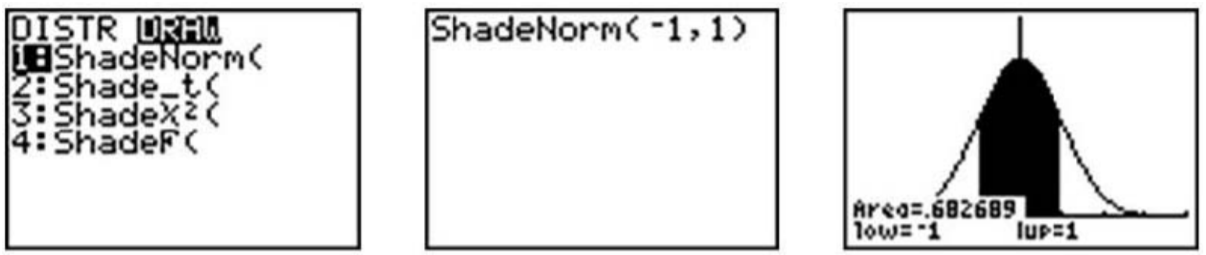
The calculator also gives a very accurate estimate of the area. We can see from the rightmost screenshot above that approximately 68% of the area is within one standard deviation of the mean. If we venture to 2 standard deviations away from the mean, how much of the data should we expect to capture? Make the following changes to the ‘ShadeNorm(’ command to find out:
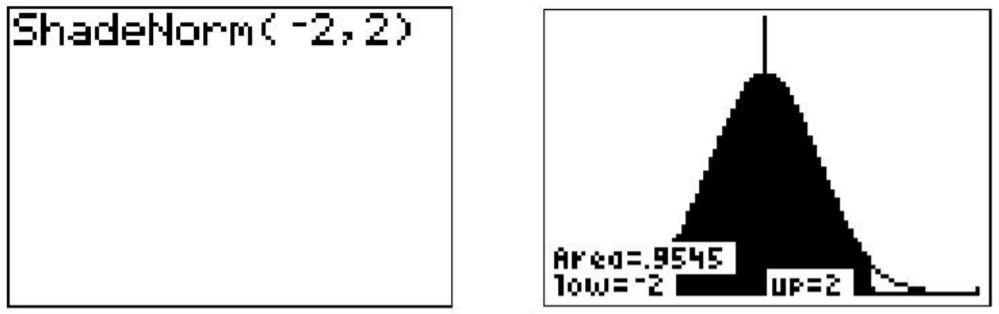
Notice from the shading that almost all of the distribution is shaded, and the percentage of data is close to 95%. If you were to venture to 3 standard deviations from the mean, 99.7%, or virtually all of the data, is captured, which tells us that very little of the data in a normal distribution is more than 3 standard deviations from the mean.
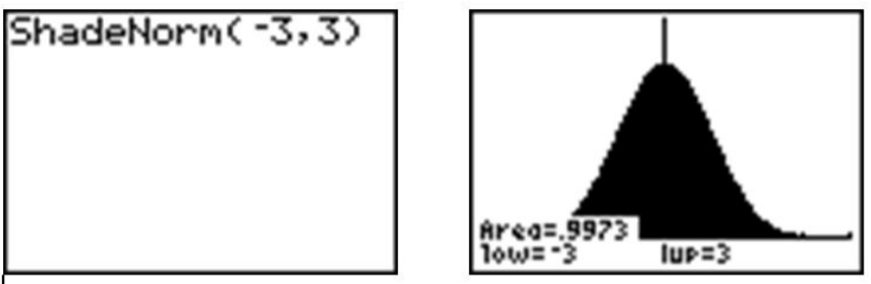
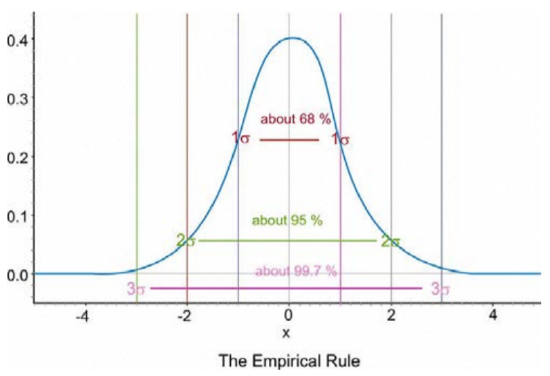
Notice that the calculator actually makes it look like the entire distribution is shaded because of the limitations of the screen resolution, but as we have already discovered, there is still some area under the curve further out than that. These three approximate percentages, 68%, 95%, and 99.7%, are extremely important and are part of what is called the Empirical Rule.
The Empirical Rule states that the percentages of data in a normal distribution within 1, 2, and 3 standard deviations of the mean are approximately 68%, 95%, and 99.7%, respectively.
On the Web
http://tinyurl.com/2ue78u Explore the Empirical Rule.
Calculating and Interpreting z-Scores
A z-score is a measure of the number of standard deviations a particular data point is away from the mean. For example, let’s say the mean score on a test for your statistics class was an 82, with a standard deviation of 7 points. If your score was an 89, it is exactly one standard deviation to the right of the mean; therefore, your z-score would be 1. If, on the other hand, you scored a 75, your score would be exactly one standard deviation below the mean, and your z-score would be −1. All values that are below the mean have negative z-scores, while all values that are above the mean have positive z-scores. A z-score of −2 would represent a value that is exactly 2 standard deviations below the mean, so in this case, the value would be 82−14=68.
To calculate a z-score for which the numbers are not so obvious, you take the deviation and divide it by the standard deviation.
z=deviationstandard deviation
You may recall that deviation is the mean value of the variable subtracted from the observed value, so in symbolic terms, the z-score would be:
z=x−µσ
As previously stated, since σ is always positive, z will be positive when x is greater than µ and negative when x is less than µ. A z-score of zero means that the term has the same value as the mean. The value of z represents the number of standard deviations the given value of x is above or below the mean.
Example 11.1.1
What is the z-score for an A on the test described above, which has a mean score of 82? (Assume that an A is a 93.)
Solution
The z-score can be calculated as follows:
z=x−µσ
z=93−827
z≈1.57
If we know that the test scores from the last example are distributed normally, then a z-score can tell us something about how our test score relates to the rest of the class. From the Empirical Rule, we know that about 68% of the students would have scored between a z-score of −1 and 1, or between a 75 and an 89, on the test. If 68% of the data is between these two values, then that leaves the remaining 32% in the tail areas. Because of symmetry, half of this, or 16%, would be in each individual tail.
Example 11.1.2
On a nationwide math test, the mean was 65 and the standard deviation was 10. If Robert scored 81, what was his z-score?
Solution
z=x−µσ
z=81−6510
z≈1.60
Example 11.1.3
On a college entrance exam, the mean was 70, and the standard deviation was 8. If Helen’s zscore was −1.5, what was her exam score?
Solution
Since z=x−µσ, then we can rewrite this formula solving for x:
x=µ+zσ
Now, we can obtain Helen's exam score with the given parameters:
x=µ+zσ
x=70+(−1.5)(8)
x=58
Thus, Helen’s exam score was 58; notice a score of 58 is below the mean and this makes sense since her z-score was negative.
Assessing Normality
The best way to determine if a data set approximates a normal distribution is to look at a visual representation. Histograms and box plots can be useful indicators of normality, but they are not always definitive. It is often easier to tell if a data set is not normal from these plots.
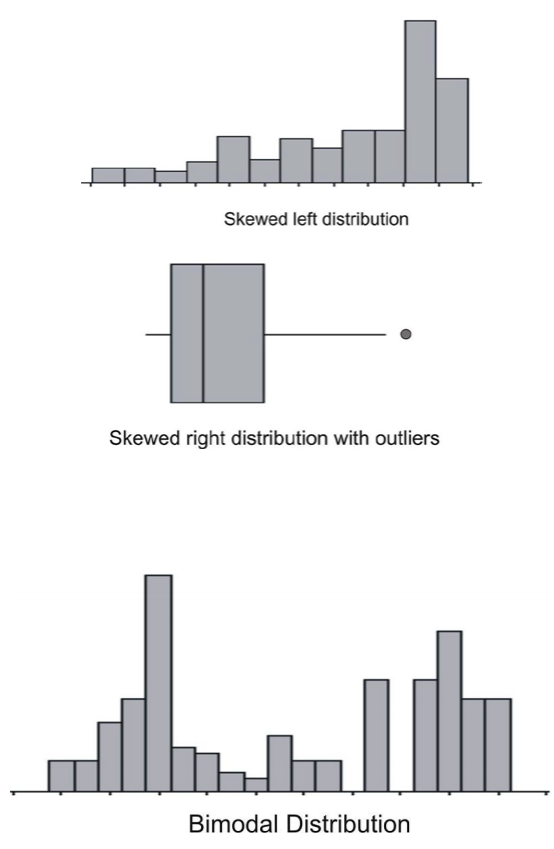
If a data set is skewed right, it means that the right tail is significantly longer than the left. Similarly, skewed left means the left tail has more weight than the right. A bimodal distribution, on the other hand, has two modes, or peaks. For instance, with a histogram of the heights of American 30-yearold adults, you will see a bimodal distribution−one mode for males and one mode for females.
There is a plot we can use to determine if a distribution is normal called a normal probability plot or normal quantile plot. To make this plot by hand, first order your data from smallest to largest. Then, determine the quantile of each data point. Finally, using a table of standard normal probabilities, determine the closest z-score for each quantile. Plot these z-scores against the actual data values. To make a normal probability plot using your calculator, enter your data into a list, then use the last type of graph in the STAT PLOT menu, as shown below:

If the data set is normal, then this plot will be perfectly linear. The closer to being linear the normal probability plot is, the more closely the data set approximates a normal distribution.
Look below at the histogram and the normal probability plot for the same data.
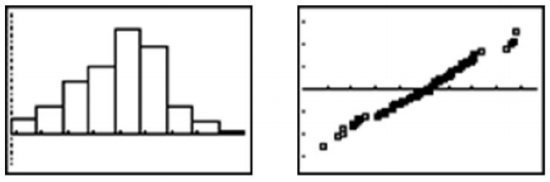
The histogram is fairly symmetric and mound-shaped and appears to display the characteristics of a normal distribution. When the z-scores of the quantiles of the data are plotted against the actual data values, the normal probability plot appears strongly linear, indicating that the data set closely approximates a normal distribution. The following example will allow you to see how a normal probability plot is made in more detail.
Example 11.1.4
The following data set tracked high school seniors’ involvement in traffic accidents. The participants were asked the following question: “During the last 12 months, how many accidents have you had while you were driving (whether or not you were responsible)?”
Solution
| Year | Percentage of high school seniors who said they were involved in no traffic accidents |
| 1991 | 75.7 |
| 1992 | 76.9 |
| 1993 | 76.1 |
| 1994 | 75.7 |
| 1995 | 75.3 |
| 1996 | 74.1 |
| 1997 | 74.4 |
| 1998 | 74.4 |
| 1999 | 75.1 |
| 2000 | 75.1 |
| 2001 | 75.5 |
| 2002 | 75.5 |
| 2003 | 75.8 |
Figure: Percentage of high school seniors who said they were involved in no traffic accidents.
Source: Sourcebook of Criminal Justice Statistics: http://www.albany.edu/sourcebook/pdf/t352.pdf
Here is a histogram and a box plot of this data:
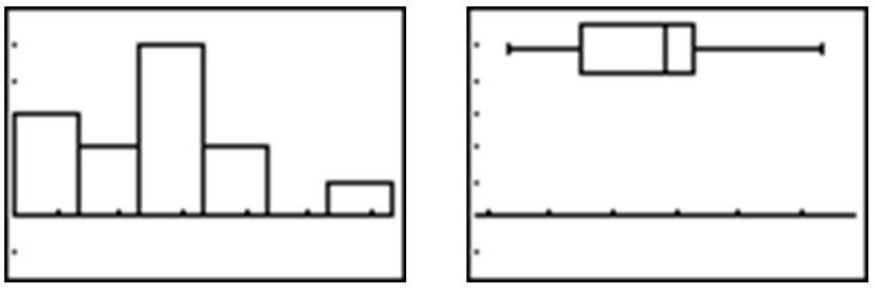
The histogram appears to show a roughly mound-shaped and symmetric distribution. The box plot does not appear to be significantly skewed, but the various sections of the plot also do not appear to be overly symmetric, either. In the following chart, the data has been reordered from smallest to largest, the quantiles have been determined, and the closest corresponding z-scores have been found using a table of standard normal probabilities.
| Table of Quantiles and Corresponding z-scores for Senior No-accident Data. | |||
|---|---|---|---|
| Year | Percentage of high school seniors who said they were involved in no traffic accidents | Quantiles | z-score |
| 1996 | 74.1 | 113=0.078 | -1.42 |
| 1997 | 74.4 | 213=0.154 | -1.02 |
| 1998 | 74.4 | 313=0.231 | -0.74 |
| 1999 | 75.1 | 413=0.286 | -0.56 |
| 2000 | 75.1 | 513=0.385 | -0.29 |
| 1995 | 75.3 | 613=0.462 | -0.09 |
| 2001 | 75.5 | 713=0.538 | 0.1 |
| 2002 | 75.5 | 813=0.615 | 0.29 |
| 1991 | 75.7 | 913=0.692 | 0.59 |
| 1994 | 75.7 | 1013=0.769 | 0.74 |
| 2003 | 75.8 | 1113=0.846 | 1.02 |
| 1993 | 76.1 | 1213=0.923 | 1.43 |
| 1992 | 76.9 | 1313=1 | 3.49 |
Here is a plot of the percentages versus the z-scores of their quantiles, or the normal probability plot:
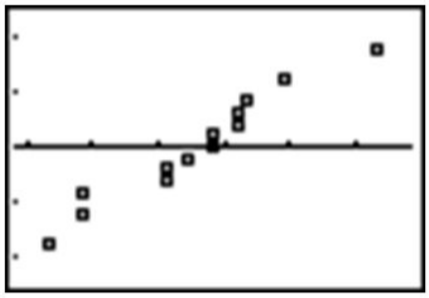
Remember that you can simplify this process by simply entering the percentages into a L1 in your calculator and selecting the normal probability plot option (the last type of plot) in STAT PLOT.
While not perfectly linear, this plot does have a strong linear pattern, and we would, therefore, conclude that the distribution is reasonably normal.
Exercises
1. Which of the following data sets is most likely to be normally distributed? For the other choices, explain why you believe they would not follow a normal distribution.
a) The hand span (measured from the tip of the thumb to the tip of the extended 5th finger) of a random sample of high school seniors
b) The annual salaries of all employees of a large shipping company
c) The annual salaries of a random sample of 50 CEOs of major companies, 25 women and 25 men
d) The dates of 100 pennies taken from a cash drawer in a convenience store
2. The grades on a statistics mid-term for a high school are normally distributed, with µ=81 and σ=6.3. Calculate the z-scores for each of the following exam grades. Draw and label a sketch for each example. 65, 83, 93, 100
3. Assume that the mean weight of 1-year-old girls in the USA is normally distributed, with a mean of about 9.5 kilograms and a standard deviation of approximately 1.1 kilograms. Without using a calculator, estimate the percentage of 1-year-old girls who meet the following conditions. Draw a sketch and shade the proper region for each problem.
a) Less than 8.4 kg
b) Between 7.3 kg and 11.7 kg
c) More than 12.8 kg
4. For a standard normal distribution, place the following in order from smallest to largest.
a) The percentage of data below 1
b) The percentage of data below −1
c) The mean
d) The standard deviation
e) The percentage of data above 2
5. The 2007 AP Statistics examination scores were not normally distributed, with µ=2.8 and σ=1.34 [1]. What is the approximate z-score that corresponds to an exam score of 5? (The scores range from 1 to 5.)
a) 0.786
b) 1.46
c) 1.64
d) 2.20
e) A z-score cannot be calculated because the distribution is not normal.
6. The heights of 5th-grade boys in the USA is approximately normally distributed, with a mean height of 143.5 cm and a standard deviation of about 7.1 cm. What is the probability that a randomly chosen 5th-grade boy would be taller than 157.7 cm?
7. A statistics class bought some sprinkle (or jimmies) doughnuts for a treat and noticed that the number of sprinkles seemed to vary from doughnut to doughnut, so they counted the sprinkles on each doughnut.
Here are the results: 241, 282, 258, 223, 133, 335, 322, 323, 354, 194, 332, 274, 233, 147, 213, 262, 227, and 366.
Create a histogram, dot plot, or box plot for this data. Comment on the shape, center, and spread of the distribution.


