1.4.1: Radical Expressions
- Page ID
- 93978
By the end of this section, you will be able to:
- Simplify expressions with roots
- Estimate and approximate roots
- Simplify variable expressions with roots
Before you get started, take this readiness quiz.
1. Simplify
a. \((−9)^{2}\)
b. \(-9^{2}\)
2. Round \(3.846\) to the nearest hundredth.
3. Simplify
a. \(x^{3} \cdot x^{3}\)
b. \(y^{2} \cdot y^{2}\)
In this section we deal with radical expressions of index \(2\) called square roots.
Simplify Expressions with Roots
In Foundations, we briefly looked at square roots. Remember that when a real number \(n\) is multiplied by itself, we write \(n^{2}\) and read it '\(n\) squared’. This number is called the square of \(n\), and \(n\) is called the square root. For example,
\(13^{2}\) is read "\(13\) squared"
\(169\) is called the square of \(13\), since \(13^{2}=169\)
\(13\) is called a square root of \(169\)
Square
If \(n^{2}=m\), then \(m\) is the square of \(n\).
Square Root
If \(n^{2}=m\), then \(n\) is a square root of \(m\).
In words,
a square root of \(m\) is a number whose square is \(m\).
Notice \((−13)^{2} = 169\) also, so \(−13\) is also a square root of \(169\). Therefore, both \(13\) and \(−13\) are square roots of \(169\).
So, every positive number has two square roots—one positive and one negative. What if we only wanted the positive square root of a positive number? We use a radical sign, and write, \(\sqrt{m}\), which denotes the positive square root of \(m\). The non-negative square root is also called the principal square root. This is the square root approximated by using the root symbol of your calculator!
We also use the radical sign for the square root of zero. Because \(0^{2}=0, \sqrt{0}=0\). Notice that zero has only one square root.
\(\sqrt{m}\) is read "the square root of \(m\)."
If \(n^{2}=m\), then \(n=\sqrt{m}\), for \(n\geq 0\).
We know that every positive number has two square roots and the radical sign indicates the positive one. We write \(\sqrt{169}=13\). If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, \(-\sqrt{169}=-13\).
Simplify:
a. \(\sqrt{144}\)
b. \(-\sqrt{289}\)
- Solution
-
a.
\(\sqrt{144}\)
Since \(12^{2}=144\), and \(12\geq 0\)
\(12\)
b.
\(-\sqrt{289}\)
Since \(17^{2}=289\), \(17\geq 0\), and the negative is in front of the radical sign.
\(-17\)
Simplify:
a. \(-\sqrt{64}\)
b. \(\sqrt{225}\)
- Answer
-
a. \(-8\)
b. \(15\)
Simplify:
a. \(\sqrt{100}\)
b. \(-\sqrt{121}\)
- Answer
-
a. \(10\)
b. \(-11\)
Can we simplify \(\sqrt{-49}\)? Is there a number whose square is \(-49\)?
\((\)___\( )^{2}=-49\)
Any positive number squared is positive. Any negative number squared is positive. There is no real number equal to \(\sqrt{-49}\). The square root of a negative number is not a real number.
Simplify:
a. \(\sqrt{-196}\)
b. \(-\sqrt{64}\)
- Solution
-
a.
\(\sqrt{-196}\)
There is no real number whose square is \(-196\).
\(\sqrt{-196}\) is not a real number.
b.
\(-\sqrt{64}\)
The negative is in front of the radical.
\(-8\)
Simplify:
a. \(\sqrt{-169}\)
b. \(-\sqrt{81}\)
- Answer
-
a. not a real number
b. \(-9\)
Simplify:
a. \(-\sqrt{49}\)
b. \(\sqrt{-121}\)
- Answer
-
a. \(-7\)
b. not a real number
Properties of \(\sqrt{a}\)
When
- \(a \geq 0\), then \(\sqrt{a}\) is a real number.
- \(a<0\), then \(\sqrt{a}\) is not a real number.
Simplify Variable Expressions with Square Roots
Note, for example,
\[\sqrt{4^2}=\sqrt{16}=4\nonumber\]
but,
\[\sqrt{(-4)^2}=\sqrt{16}=4,\nonumber\]
So that the result is positive.
How can we make sure the square root of \(−5\) squared is \(5\)? We can use the absolute value. \(|−5|=5\): \[\sqrt{a^{2}}=|a|.\] This guarantees the principal root is positive.
Note that the 'root button' and the 'square button' are the same on most calculators and if \(a\) is positive, applying the square button and then the root button (or vice versa) will result in the return of \(a\).
We have
\(\sqrt{a^{2}}=|a|\)
Simplify \(\sqrt{x^{2}}\).
- Solution
-
We use the absolute value to be sure to get the positive root.
\(\sqrt{x^{2}}=|x|\)
Simplify \(\sqrt{b^{2}}\).
- Answer
-
\(|b|\)
What about square roots of higher powers of variables? The power property of exponents says \(\left(a^{m}\right)^{n}=a^{m \cdot n}\). So if we square \(a^{m}\), the exponent will become \(2m\).
\(\left(a^{m}\right)^{2}=a^{2 m}\)
Looking now at the square root.
\(\sqrt{a^{2 m}}=\sqrt{\left(a^{m}\right)^{2}}\)
Since \(2\) is even, \(\sqrt[2]{x^{2}}=|x|\). So
\[\sqrt{a^{2 m}}=\left|a^{m}\right|.\]
We apply this concept in the next example.
Simplify:
a. \(\sqrt{x^{6}}\)
b. \(\sqrt{y^{16}}\)
- Solution
-
a.
\(\sqrt{x^{6}}\)
Since \(\left(x^{3}\right)^{2}=x^{6}\), this is equal to
\(\sqrt{\left(x^{3}\right)^{2}}.\)
Since \(\sqrt{a^{2}}=|a|\), this is equal to
\(\left|x^{3}\right|\)
b.
\(\sqrt{y^{16}}\)
Since \(\left(y^{8}\right)^{2}=y^{16}\), this is equal to
\(\sqrt{\left(y^{8}\right)^{2}}.\)
Since \(\sqrt{a^{2}}=|a|\), this is equal to
\(y^{8}\)
In this case the absolute value sign is not needed as \(y^{8}\) is positive.
Simplify:
a. \(\sqrt{y^{18}}\)
b. \(\sqrt{z^{12}}\)
- Answer
-
a. \(|y^{9}|\)
b. \(z^{6}\)
Simplify:
a. \(\sqrt{m^{4}}\)
b. \(\sqrt{b^{10}}\)
- Answer
-
a. \(m^{2}\)
b. \(|b^{5}|\)
Note that if the variables are positive, then the exponent gets halved which is the same action you would do to simplify \(( )^{\frac12}\) if rational exponents followed the same rules as integer exponents. For example, if \(x\) is non-negative,
\(\sqrt{x^{6}}=(x^6)^\frac12=x^{6\cdot\dfrac12}=x^3.\)
We will treat this in greater detail a little later in this chapter.
In the next example, we now have a coefficient in front of the variable. The concept \(\sqrt{a^{2 m}}=\left|a^{m}\right|\) works in much the same way.
\(\sqrt{16 r^{22}}=4\left|r^{11}\right|\) because \(\left(4 r^{11}\right)^{2}=16 r^{22}\).
But notice \(\sqrt{25 u^{8}}=5 u^{4}\) and no absolute value sign is needed as \(u^{4}\) is always non-negative.
Simplify:
a. \(\sqrt{16 n^{2}}\)
b. \(-\sqrt{81 c^{2}}\)
- Solution
-
a.
\(\sqrt{16 n^{2}}\)
Since \((4 n)^{2}=16 n^{2}\), this is equal to
\(\sqrt{(4 n)^{2}}.\)
Since \(\sqrt{a^{2}}=|a|\), this is equal to
\(4|n|.\)
b.
\(-\sqrt{81 c^{2}}\)
Since \((9 c)^{2}=81 c^{2}\), this is equal to
\(-\sqrt{(9 c)^{2}}.\)
Since \(\sqrt{a^{2}}=|a|\), this is then equal to
\(-9|c|.\)
Simplify:
a. \(\sqrt{64 x^{2}}\)
b. \(-\sqrt{100 p^{2}}\)
- Answer
-
a. \(8|x|\)
b. \(-10|p|\)
Simplify:
a. \(\sqrt{169 y^{2}}\)
b. \(-\sqrt{121 y^{2}}\)
- Answer
-
a. \(13|y|\)
b. \(-11|y|\)
The next examples have two variables.
Simplify:
a. \(\sqrt{36 x^{2} y^{2}}\)
b. \(\sqrt{121 a^{6} b^{8}}\)
- Solution
-
a.
\(\sqrt{36 x^{2} y^{2}}\)
Since \((6 x y)^{2}=36 x^{2} y^{2}\)
\(\sqrt{(6 x y)^{2}}\)
Take the square root.
\(6|xy|\)
b.
\(\sqrt{121 a^{6} b^{8}}\)
Since \(\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}\)
\(\sqrt{\left(11 a^{3} b^{4}\right)^{2}}\)
Take the square root.
\(11\left|a^{3}\right| b^{4}\)
Simplify:
a. \(\sqrt{100 a^{2} b^{2}}\)
b. \(\sqrt{144 p^{12} q^{20}}\)
- Answer
-
a. \(10|ab|\)
b. \(12p^{6}q^{10}\)
Simplify:
a. \(\sqrt{225 m^{2} n^{2}}\)
b. \(\sqrt{169 x^{10} y^{14}}\)
- Answer
-
a. \(15|mn|\)
b. \(13\left|x^{5} y^{7}\right|\)
- What is a square root?
- Explain why \(\sqrt{9}=3\).
- What happens if we square a square root?
- What is the index? Radicand?
Simplify \(\sqrt{81a^4b^6}\).
Key Concepts
- Square Root Notation
- \(\sqrt{m}\) is read ‘the square root of \(m\)’
- If \(n^{2}=m\), then \(n=\sqrt{m}\), for \(n≥0\).
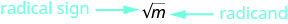
Figure 8.1.1 - The square root of \(m\), \(\sqrt{m}\), is a positive number whose square is \(m\).
- Properties of \(\sqrt{a}\)
- \(a≥0\), then \(\sqrt{a}\) is a real number
- \(a<0\), then \(\sqrt{a}\) is not a real number
- Simplifying Odd and Even Roots
- \(\sqrt{a^{2}}=|a|\). We must use the absolute value signs when we take a square root of an expression with a variable in the radical.