4.2: Trigonometric Equations
- Page ID
- 94229
By the end of this section, you will be able to:
- Find two specific solutions to simple trigonometric equations.
- Draw a picture of the unit circle illustrating the solutions to certain simple trigonometric equations.
Before you get started, take this readiness quiz.
- Draw a picture of a triangle where one vertex is the origin, one is on the unit circle in the 2nd quadrant and one is on the \(x\)-axis.
- Draw a picture of a triangle where on vertex is the origin, one is on the unit circle and in the 4th quadrant and one is on th \(x\)-axis.
- If in the picture above, the coordinates of the vertex which is on the unit circle has coordinates \((3,-4)\), find the lengths of the sides of triangle.
An equation involving trigonometric functions is called a trigonometric equation. For example, an equation like
\[ \cos A = 0.75,
\nonumber \]
which we encountered in while solving right triangles, is a trigonometric equation. There we were concerned only with finding a single solution (say, between \(0° \) and \(90°\)). In this section we will be concerned with finding the most general solution to such equations.
To see what that means, we first look at the example:
Solve \(\cos A = 0.75\) where \(0° \leq A<360°\).
Solution
Using the \(\fbox{\(\cos^{-1}\)}\) calculator button in degree mode, we get \(A= 41.41° \). However, we know the \(\cos A\) is the \(x\)-coordinate of the point on the unit circle intersecting with the terminal side of the angle \(A\). This \(x\)-coordinate is given as positive, viz., \(.75\), so we draw two possibilities (the drawing needn't be precise but only indicate relationships accurately):
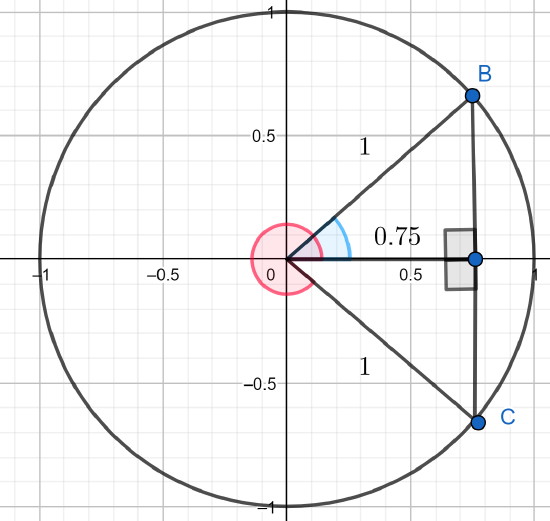
The points \(B\) and \(C\) are the points on the unit circle with \(x\)-coordinate \(0.75\). To these coorespond two angles, one in blue and one in red. Calling the blue angle \(A\) for the moment, we find that \(A\) is an angle of a right triangle and \(\cos A=.75\) so that \(A=41.41°\) as found above by using the calculator. The angle of the other right triangle (in the 4th quadrant) is congruent (same size and shape) of the triangle in the first quadrant and so the angle at the origin is also \(38.68°\). It follows that, since the sum of the red angle and \(41.41°\) is \(360°\), the red angle is \((360-41.41)°=319.59° \).
These are the solutions of the equation that are in \([0,360°)\). There are many more since we should also look at all possible co-terminal angles. For example \(360+41.41\) degrees. There are an infinite number of solutions if we do not consider the restriction \(0° \leq A<360°\).
Solve \(\cos \theta=-\dfrac12\) if \(0° \leq \theta <360°\).
- Answer
-
\(\theta=120°\) or \(\theta=240°\)
Solve \(\tan x=-\dfrac13\) if \(0 \leq \theta < 2\pi\) (radians). Round your answer to the nearest hundredth.
- Answer
-
\(x= 2.82\) or \(x=5.96\) radians.
Try the following examples before looking at the detailed solutions.
Solve the equation \(2\sin\theta + 1 = 0 \).
Solution:
Isolating \(\sin\theta \) gives \(\sin\theta = -\dfrac{1}{2} \).
Recall that the sin ratio is \(y\)-coordinate on the unit circle. This is negative (negative \(\dfrac12\)). So, we can sketch the possibilities by marking the point on the unit circle with \(y\)-coordinate equal to \(-\dfrac12\)
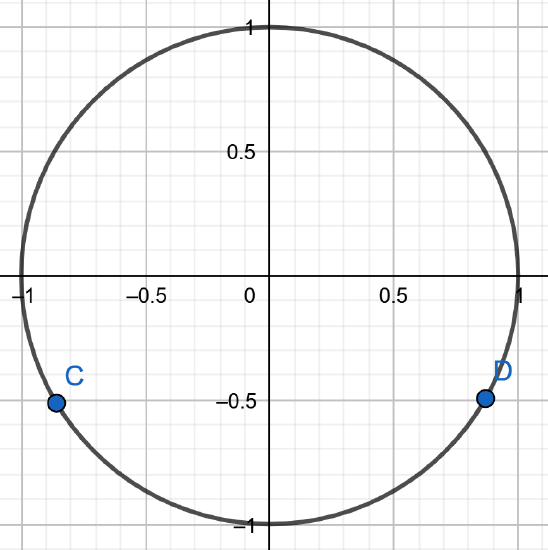
and then to construct two congruent triangles (called reference triangles).
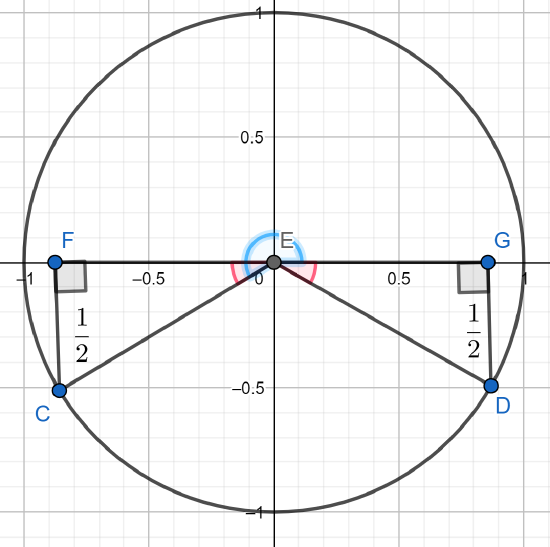
The two triangles are congruent and the red angles are the same.
Noting that the triangle is a similar to the 30-60-90 triangle we see that the red angles are \(\dfrac{\pi}{6}\). We could also use the \(\fbox{\(\sin^{-1}\)}\) calculator button in degree mode which gives us \(\theta = -30°\) only the angle in quadrant IV. To find the blue angle, we have to see how it relates to the red angle. The blue angle minus the red angle is a straight angle. So our blue angle is \(180+30=210°\) or in radians \(\pi+\dfrac{\pi}{6}=\dfrac{7\pi}{6}\). So two solutions are (and all others are coterminal)
\[\theta=-30°\text{ or }\theta=210°.\]
If we want find the solutions in \([0,360°]\) we will need to add \(360°\) to the \(-30°\) to get \(330°\) so,
If \(2\sin\theta + 1 = 0 \) and \(\theta \) is in \([0,360°)\) then
\[\theta=330°\text{ or }\theta=210°.\]
In radians, the solution is:
If \(2\sin\theta + 1 = 0 \) and \(\theta\) is in \([0,2\pi)\) then
\[ \boxed{\theta = \dfrac{11\pi}{6}\quad { or }\quad \dfrac{7\pi}{6}}\]
All other solutions are co-terminal to these.
Solve the equation \(2\cos^2\theta - 1 = 0 \), where \(\theta\) is in \([0,2\pi)\).
Solution:
Isolating \(\cos^2 \theta \) gives us
\[ \cos^2 \theta = \dfrac{1}{2} \quad\Rightarrow\quad \cos\theta = \pm\dfrac{1}{\sqrt{2}}\]
Noting that this means the \(x\)-coordinate of points on the unit circle associated with \(\theta\) are \(\pm\dfrac{1}{\sqrt{2}}\).
.png?revision=1&size=bestfit&width=344&height=334)
Each of the triangles are special triangles and the angles at the origin are all \(\dfrac{\pi}{4}\). So we have that
if \(2\cos^2 \theta - 1 = 0 \), where \(\theta\) is in \([0,2\pi)\),
then
\[\theta=\dfrac{\pi}{4},\dfrac{3\pi}{4},\dfrac{5\pi}{4},\text{ or }\dfrac{7\pi}{4}.\]
Solve the equation \(2\sec\theta = 1 \).
Solution:
Isolating \(\sec\theta \) gives us
\[ \sec\theta = \dfrac{1}{2} \quad\Rightarrow\quad \cos\theta = \dfrac{1}{\sec\theta} = 2,
\nonumber \]
which is impossible. Thus, there is \(\fbox{no solution}\).
Solve the equation \(\cos\theta = \tan\theta \).
Solution:
The idea here is to use identities to put everything in terms of a single trigonometric function:
\[\nonumber \begin{align*}
\cos\theta &= \tan\theta\\ \nonumber
\cos\theta &=\dfrac{\sin\theta}{\cos\theta}\\ \nonumber
\cos^2 \theta &=\sin\theta\\ \nonumber
1 - \sin^2 \theta &= \sin\theta\\ \nonumber
0 &= \sin^2 \theta + \sin\theta - 1
\end{align*} \nonumber \]
The last equation looks more complicated than the original equation, but notice that it is actually a quadratic equation: making the substitution \(x=\sin\theta \), we have
\[ x^2 + x - 1 = 0 \quad\Rightarrow\quad x = \dfrac{-1 \pm \sqrt{1 - (4)(-1)}}{
2(1)} = \dfrac{-1 \pm\sqrt{5}}{2} = -1.618,~0.618
\nonumber \]
by the quadratic formula from elementary algebra. But \(-1.618\) can not be a \(y\)-coordinate of a point on the unit circle, so it is impossible that \(\sin\theta = x = -1.618 \). Thus, we must have \(\sin\theta = x = 0.618\). Hence, there are two possible solutions corresponding to the points on the unit circle with \(y\)-coordinate 0.618:
.png?revision=1&size=bestfit&width=392&height=388)
So, if \(\cos\theta = \tan\theta \),
then
\(\theta = 0.666\) radians or its reflection \(\pi - .666 = 2.476\) radians (or, more accurately, \(\pi-\sin^{-1} .618= 2.475\) .
Challenge examples
Try to solve the equations before looking at the solution.
Solve the equation \(\sin\theta = \tan\theta\).
Solution:
Trying the same method as in the previous example, we get
\[\nonumber \begin{align*}
\sin\theta &= \tan\theta\\ \nonumber
\sin\theta &= \dfrac{\sin\theta}{\cos\theta}\\ \nonumber
\sin\theta\cos\theta &= \sin\theta\\ \nonumber
\sin\theta\cos\theta - \sin\theta &= 0\\ \nonumber
\sin\theta(\cos\theta - 1) &= 0\\ \nonumber
\Rightarrow\quad \sin\theta = 0 \quad\text{or} &\quad \cos\theta = 1\\ \nonumber
\Rightarrow\quad \theta = 0, \pi \quad\text{or} &\quad \theta = 0\\ \nonumber
\Rightarrow\quad \theta = 0, \pi,
\end{align*} \nonumber \]
plus multiples of \(2\pi \). So since the above angles are multiples of \(\pi \), and every multiple of \(2\pi \) is a multiple of \(\pi \), we can combine the two answers into one for the general solution:
\[ \boxed{\theta = \pi k} \qquad\text{for \(k=0 \), \(\pm 1\), \(\pm 2, \dots\)}
\nonumber \]
Solve the equation \(\cos(3\theta) = \dfrac{1}{2}\).
Solution:
The idea here is to solve for \(3\theta \) first, using the most general solution, and then divide that solution by \(3 \). So since \(\cos^{-1} \left(\dfrac{1}{2}\right) = \dfrac{\pi}{3}\), there are two possible solutions for \(3\theta\): \(3\theta = \dfrac{\pi}{3}\) in QI and its reflection \(-3\theta = -\dfrac{\pi}{3} \) around the \(x\)-axis in QIV. Adding multiples of \(2\pi\) to these gives us:
\[ 3\theta = \pm\dfrac{\pi}{3} + 2\pi k \qquad\text{for \(k=0 \), \(\pm 1 \), \(\pm 2, \dots\)}
\nonumber \]
So dividing everything by \(3 \) we get the general solution for \(\theta\):
\[ \boxed{\theta = \pm\dfrac{\pi}{9} + \dfrac{2\pi}{3} k}
\qquad\text{for \(k=0 \), \(\pm 1 \), \(\pm 2, \dots \)}
\nonumber \]
Solve the equation \(2\sin\theta - 3\cos\theta = 1 \). Use the fact (not treated here) that for any angles \(A\) and \(B\),
\[\sin(A-B)=\sin(A)\cos(B)-\sin(B)\cos(A).\]
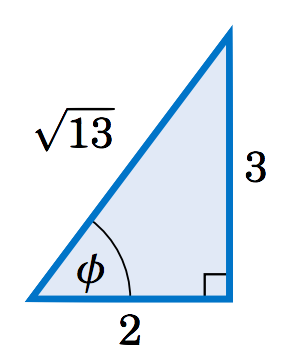
Solution
We will use the technique which we discussed in Chapter 5 for finding the amplitude of a combination of sine and cosine functions. Take the coefficients \(2 \) and \(3\) of \(\sin\theta\) and \(-\cos\theta \), respectively, in the above equation and make them the legs of a right triangle, as in Figure 6.1.1. Let \(\phi\) be the angle shown in the right triangle. The leg with length \(3 >0\) means that the angle \(\phi\) is above the \(x\)-axis, and the leg with length \(2>0\) means that \(\phi\) is to the right of the \(y\)-axis. Hence, \(\phi\) must be in QI. The hypotenuse has length \(\sqrt{13}\) by the Pythagorean Theorem, and hence \(\cos\phi = \dfrac{2}{\sqrt{13}}\) and \(\sin\theta = \dfrac{3}{\sqrt{13}}\). We can use this to transform the equation to solve as follows:
\[\nonumber \begin{align*}
2\sin\theta - 3\cos\theta &=1\\ \nonumber
\sqrt{13}\left(\dfrac{2}{\sqrt{13}}\sin\theta - \dfrac{3}{\sqrt{13}}\cos\theta
\right) &=1\\ \nonumber
\sqrt{13}(\cos\phi\sin\theta - \sin\phi\cos\theta) &= 1\\ \nonumber
\sqrt{13}\sin(\theta - \phi) &=1\quad\text{(by the sine subtraction formula)}\\ \nonumber
\sin(\theta - \phi) &= \dfrac{1}{\sqrt{13}}\\ \nonumber
\Rightarrow\quad \theta - \phi = 0.281 \quad\text{or} &\quad \theta - \phi = \pi - 0.281 = 2.861\\ \nonumber
\Rightarrow\quad \theta = \phi + 0.281 \quad\text{or}&\quad \theta = \phi + 2.861
\end{align*} \nonumber \]
Now, since \(\cos\phi = \dfrac{2}{\sqrt{13}} \) and \(\phi \) is in QI, the most general solution for \(\phi \) is \(\phi = 0.983 + 2\pi k \) for \(k=0\), \(\pm 1 \), \(\pm 2,\dots\). So since we needed to add multiples of \(2\pi \) to the solutions \(0.281 \) and \(2.861 \) anyway, the most general solution for \(\theta \) is:
\[\begin{align*}
\theta &= 0.983 + 0.281 + 2\pi k\quad\text{and}\quad 0.983 + 2.861 + 2\pi k\\
\Rightarrow\quad & \boxed{\theta = 1.264 + 2\pi k\quad\text{and}\quad 3.844 +2\pi k}
\quad\text{for \(k=0 \), \(\pm 1 \), \(\pm 2, \dots \)}
\end{align*} \nonumber \]
Note: In Example 6.8 if the equation had been \(2\sin\theta + 3\cos\theta = 1 \) then we still would have used a right triangle with legs of lengths \(2\) and \(3\), but we would have used the sine addition formula instead of the subtraction formula.
- If you know one solution to a trigonometric equaiton \(\cos(x)=a\) for a given \(a\), how can you find another which is not coterminal?
- How many solutions are there to the equation \(\sin(x)=-\dfrac12\)? Do not solve this here.
- If we replaced \(-\dfrac12\) by any other number in the previous question, would we get the same answer? Explain.
- Solve \(\cos(x)=-2\) and explain.
- Solve \(\cos(x)=-\dfrac{1}{\sqrt{2}}\), where \(0\leq x <2\pi\).
- Solve \(\sin(\theta)=-\dfrac13\), where \(0\leq \theta<360°\).
Key Concepts
- Unit circle and the trigonometric ratios
- Solutions to equations in one variable