2.1: Solving Linear Inequalities in One Variable

Last updated
Save as PDF

Page ID: 151964

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

In this section, you will learn to:

Verify solutions to linear inequalities.
Represent infinite solutions using interval notation.
Solve linear inequalities in one variable.

Prerequisite Skills

Before you get started, take this prerequisite quiz.

1. Verify if each value is a solution to the equation $3x-2(x+4)=6x+7$

a. $x=2$

b. $x=-3$

Click here to check your answer

a. No

b. Yes

If you missed any part of this problem, review Section 1.1. (Note that this will open a in a new window.)

2. Solve each equation.

a. $-2x-3=5x+11$

b. $-4x+2-x=1$

Click here to check your answer

a. $x=-2$

b. $x=\frac{1}{5}$

If you missed any part of this problem, review Section 1.1. (Note that this will open a in a new window.)

3. Determine whether each inequality is true or false.

a. $4<9$

b. $7>2$

c. $-13<-8$

d. $-5 \geq -5$

e. $-5 > -5$

f. $-100<50$

Click here to check your answer

a. True

b. False

c. True

d. True

e. False

f. True (Any negative is ALWAYS less than any positive.)

If you missed any part of this problem, review HERE. (Note that this will open a different textbook in a new window.)

Linear Inequalities

A linear inequality¹³⁸ is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:

$5 x + 7 < 22$

$- 2 ( x + 8 ) + 6 \geq 20$

$- 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 )$

Table 1.1.5

A solution to a linear inequality¹³⁹ is a real number that will produce a true statement when substituted for the variable.

Example $\PageIndex{1}$:

Are $x=−4$ and $x=6$ solutions to $5x+7<22$?

Solution

Substitute the values in for $x$, simplify, and check to see if we obtain a true statement.

Check $x=−4$	Check $x=6$
$\begin{array} { r } { 5 ( \color{Cerulean}{- 4}\color{Black}{ )} + 7 < 22 } \\ { - 20 + 7 < 22 } \\ { - 13 < 22 } \:\:\color{Cerulean}{✓} \end{array}$	$\begin{array} { c } { 5 ( \color{Cerulean}{6} \color{Black}{)} + 7 < 22 } \\ { 30 + 7 < 22 } \\ { 37 < 22 } \:\:\color{red}{✗} \end{array}$

Table 1.1.6

Answer:

$x=−4$ is a solution and $x=6$ is not

Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, we graph the solution set on a number line and/or express the solution using interval notation.

Expressing Solutions to Linear Inequalities

What number would make the inequality $x>3$ true? Are you thinking, "$x$ could be four"? That’s correct, but $x$ could be 6, too, or 137, or even 3.0001. Any number greater than three is a solution to the inequality $x>3$. We show all the solutions to the inequality $x>3$ on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three.

We can also represent inequalities using interval notation. There is no upper end to the solution to this inequality. In interval notation, we express $x>3$ as $(3,\infty)$. The symbol $\infty$ is read as “infinity.” It is not an actual number. Figure $\PageIndex{2}$ shows both the number line and the interval notation.

The figure shows the inquality, x is greater than 3, graphed on a number line from negative 5 to 5. There is shading that starts at 3 and extends to numbers to its right. The solution for the inequality is written in interval notation. It is the interval from 3 to infinity, not including 3. — Figure $\PageIndex{2}$: The inequality $x>3$ is graphed on this number line and written in interval notation.

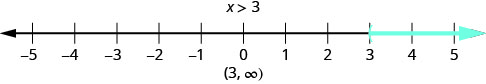
We use the left parenthesis symbol, (, to show that the endpoint of the inequality is not included. The left bracket symbol, [, would show that the endpoint is included.

The inequality $x\leq 1$ means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at $x=1$. We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions (Figure $\PageIndex{3}$). There is no lower end to those numbers. We write $x\leq 1$ in interval notation as $(−\infty,1]$. The symbol $−\infty$ is read as “negative infinity.”

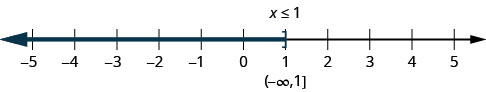
The figure shows the inquality, x is less than or equal to l, graphed on a number line from negative 5 to 5. There is shading that starts at 1 and extends to numbers to its left. The solution for the inequality is written in interval notation. It is the interval from negative infinity to one, including 1. — Figure $\PageIndex{3}$: The inequality $x\leq 1$ is graphed on this number line and written in interval notation.

Figure $\PageIndex{4}$ shows both the number line and interval notation.

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

$The figure shows that the solution of the inequality x is greater than a is indicated on a number line with a left parenthesis at a and shading to the right, and that the solution in interval notation is the interval from a to infinity enclosed in parentheses. It shows the solution of the inequality x is greater than or equal to a is indicated on a number line with an left bracket at a and shading to the right, and that the solution in interval notation is the interval a to infinity within a left bracket and right parenthesis. It shows that the solution of the inequality x is less than a is indicated on a number line with a right parenthesis at a and shading to the left, and that the solution in interval notation is the the interval negative infinity to a within parentheses. It shows that the solution of the inequality x is less than or equal to a is indicated on anumber line with a right bracket at a and shading to the left, and that the solution in interval notation is negative infinity to a within a left parenthesis and right bracket.$

The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals. Notice that $\infty$ and $-\infty$ always use parentheses in interval notation, never brackets.

Example $\PageIndex{2}$

Graph each inequality on the number line and write in interval notation.

$x\geq −3$
$x<2.5$
$x\leq −\frac{3}{5}$

Answer

	$ x \geq -3 $
Shade to the right of $−3$, and put a bracket at $−3$.	$.$
Write in interval notation.	$ [-3, \infty) $

	$ x < 2.5 $
Shade to the left of 2.5 and put a parenthesis at 2.5.	$.$
Write in interval notation.	$ (-\infty, 2.5) $

	$ x \leq -\dfrac{3}{5} $
Shade to the left of $−\frac{3}{5}$, and put a bracket at $−\frac{3}{5}$.	$.$
Write in interval notation.	$ \bigg( -\infty, \dfrac{3}{5}\bigg] $

Exercise $\PageIndex{1}$

Graph each inequality on the number line and write in interval notation:

$x\leq −4$
$x\geq 0.5$
$x<−\frac{2}{3}$.

Answer

ⓐ

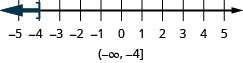
$The graph of the inequality x is less than or equal to negative 4 is indicated on a number line with a right bracket at negative 4 and shading to the left. The solution in interval notation is the interval from negative infinity to negative 4 enclosed within an left parenthesis and right bracket.$

ⓑ

$The graph of the inequality x is greater than or equal to 0.5 is indicated on a number line with a left bracket at 0.5 and shading to the right. The solution in interval notation is the interval from 0.5 to infinity enclosed within a left bracket and right parenthesis.$

ⓒ

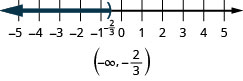
$The graph of the inequality x is less than negative two-thirds is indicated on a number line with a right parenthesis at negative two-thirds and shading to the left. The solution in interval notation is the interval from negative infinity to negative two-thirds enclosed within parentheses.$

Solving Linear Inequalities

Recall the following properties of equality from Section 1.1. Given algebraic expressions $A$ and $B$, and real number $c$:

Addition property of equality:	If $A=B$, then $A\color{Cerulean}{+c}\color{Black} = B\color{Cerulean}{+c}$
Subtraction property of equality:	If $A=B$, then $A\color{Cerulean}{-c}\color{Black} = B\color{Cerulean}{-c}$
Multiplication property of equality:	If $A=B$, then $\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}$
Division property of equality:	If $A=B$, then $\frac{A}{\color{Cerulean}{c}}\color{Black} = \frac{B}{\color{Cerulean}{c}}, \color{Cerulean}{c}\color{Black} \neq {0}$

All but one of the techniques learned for solving linear equations apply to solving linear inequalities. You may add or subtract any real number to both sides of an inequality, and you may multiply or divide both sides by any positive real number to create equivalent inequalities.

Example $\PageIndex{3}$:

Solve and graph the solution set: $5x+7<22$.

Solution

$\begin{array} { c } { 5 x + 7 < 22 } \\ { 5 x + 7 \color{Cerulean}{- 7}\color{Black}{ < 22}\color{Cerulean}{ - 7} } \\ { 5 x < 15 } \\ { \frac { 5 x } {\color{Cerulean}{ 5} } < \frac { 15 } { \color{Cerulean}{5} } } \\ { x < 3 } \end{array}$

It is helpful to take a minute and choose a few values in and out of the solution set, substitute them into the original inequality, and then verify the results. As indicated, you should expect $x=0$ to solve the original inequality and that $x=5$ should not.

Check $x=0$	Check $x=5$
$\begin{array} { r } { 5 ( \color{Cerulean}{0}\color{Black}{ )} + 7 < 22 } \\ { 7 < 22 }\:\:\color{Cerulean}{✓} \end{array}$	$\begin{array} { r } { 5 ( \color{Cerulean}{5}\color{Black}{ )} + 7 < 22 } \\ { 25 + 7 < 22 } \\ { 32 < 22 } \:\:\color{red}{✗} \end{array}$

Checking in this manner gives us a good indication that we have solved the inequality correctly.

Answer

$(−∞, 3) $

When working with linear inequalities, different rules apply when multiplying or dividing by a positive number vs. a negative number. To illustrate the problem, consider the true statement $10 > −5$. We'll divide both sides by $5$ and then by $−5$.

$\begin{array} { l } { 10 > - 5 } \quad \color{Cerulean}{✓} \color{Cerulean}{ True } \\ { \frac {10} { \color{Cerulean}{ 5} } \color{Black}{>} \frac { - 5 } { \color{Cerulean}{ 5} } } \quad \color{Cerulean}{Divide\: both\: sides\: by\: 5.} \\ { 2 \color{Black}{>}\color{Black}{- 1} \quad \color{Cerulean}{✓} \color{Cerulean}{ Still\: True} } \end{array}$

Dividing both sides of the inequality by $5$ kept the statement true. Dividing both sides of any inequality by $c>0$ will be the same process as solving a linear equation.

$\begin{array} { l } { 10 > - 5 } \quad \color{Cerulean}{✓} \color{Cerulean}{ True } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{>} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Divide\: both\: sides\: by\: -5.} \\ { - 2 \color{red}{>}\color{Black}{ 1} \quad \color{red}{✗} \color{red}{ False } } \end{array}$

Dividing by $−5$ results in a false statement since $c<0$. To retain a true statement, the inequality must be reversed.

$\begin{array} { l } { 10 > - 5 } \quad \color{Cerulean}{✓} \color{Cerulean}{ True } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{>} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Divide\: both\: sides\: by\: -5 \: and\: flip\: the\: inequality.} \\ { - 2 \color{Black}{<}\color{Black}{ 1} \quad \color{Cerulean}{✓} \color{Cerulean}{ Still\: True} } \end{array}$

The same problem occurs when multiplying by a negative number. This leads to the following new rule: when multiplying or dividing by a negative number, reverse the inequality. It is easy to forget to do this so take special care to watch for negative coefficients. In general, given algebraic expressions $A$ and $B$, and real number $c$, we have the following properties of inequalities¹⁴⁰:

Addition property of inequalities:	If $A<B$ then, $A \color{Cerulean}{+c}\:\color{Black}{<}\:B\color{Cerulean}{+c}$
Subtraction property of inequalities:	If $A<B$ then, $A \color{Cerulean}{-c}\:\color{Black}{<}\:B\color{Cerulean}{-c}$
Multiplication property of inequalities:	If $A<B$, then $\color{Cerulean}{c}\color{Black}{A}\:<\:\color{Cerulean}{c}\color{Cerulean}\color{Black}{B}$ If $A<B$, then $\color{Cerulean}{-c}\color{Black}{A}\:\color{OliveGreen}{>}\:\color{Cerulean}{-c}\color{Cerulean}\color{Black}{B}$
Division property of inequalities:	If $A<B$, then $\frac{A}{\color{Cerulean}{c}}\color{Black}{<}\frac{B}{\color{Cerulean}{c}}, \color{Cerulean}{c}\color{Black} \neq {0}$ If $A<B$, then $\frac{A}{\color{Cerulean}{-c}}\color{OliveGreen}{>}\frac{\color{Black}{B}}{\color{Cerulean}{-c}}, \color{Cerulean}{c}\color{Black} \neq {0}$

Table 1.1.8

We use these properties to obtain an equivalent inequality¹⁴¹, one with the same solution set, where the variable is isolated. The process is similar to solving linear equations.

Example $\PageIndex{4}$:

Solve and graph the solution set: $−2(x+8)+6≥20$.

Solution

$\begin{aligned} - 2 ( x + 8 ) + 6 & \geq 20 \quad\color{Cerulean}{Distribute.} \\ - 2 x - 16 + 6 & \geq 20 \quad\color{Cerulean}{Combine\: like\: terms.} \\ - 2 x - 10 & \geq 20 \quad\color{Cerulean}{Solve\: for\: x.} \\ - 2 x & \geq 30 \quad\color{Cerulean}{Divide\: both\: sides\: by\: -2.} \\ \frac { - 2 x } { \color{Cerulean}{- 2} } & \color{OliveGreen}{\leq} \frac { \color{Black}{30} } { \color{Cerulean}{- 2} } \quad\color{Cerulean}{Reverse\: the\: inequality.} \\ x & \leq - 15 \end{aligned}$

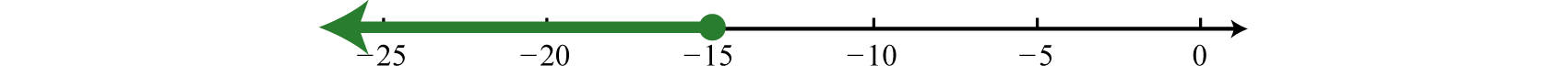
Answer:

Interval notation $(−∞, −15] $

Example $\PageIndex{5}$:

Solve and graph the solution set: $−2(4x−5)<9−2(x−2)$.

Solution

$\begin{array} { c } { - 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 ) } \\ { - 8 x + 10 < 9 - 2 x + 4 } \\ { - 8 x + 10 < 13 - 2 x } \\ { - 6 x < 3 } \\ { \frac { - 6 x } { \color{Cerulean}{- 6} } \color{OliveGreen}{>} \frac { \color{Black}{3} } { \color{Cerulean}{- 6} } }\color{Cerulean}{Reverse\:the\:inequality.} \\ { x > - \frac { 1 } { 2 } } \end{array}$

Answer:

Interval notation $(−\frac{1}{2}, ∞)$

Example $\PageIndex{6}$:

Solve and graph the solution set: $\frac{1}{2}x−2≥\frac{1}{2}(\frac{7}{4}x−9)+1$.

Solution

$\begin{array} { c } { \frac { 1 } { 2 } x - 2 \geq \frac { 1 } { 2 } \left( \frac { 7 } { 4 } x - 9 \right) + 1 } \\ { \frac { 1 } { 2 } x - 2 \geq \frac { 7 } { 8 } x - \frac { 9 } { 2 } + 1 } \\ { \frac { 1 } { 2 } x - \frac { 7 } { 8 } x \geq - \frac { 7 } { 2 } + 2 } \\ { - \frac { 3 } { 8 } x \geq - \frac { 3 } { 2 } } \\ { \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left(\color{Black}{ - \frac { 3 } { 8 } x} \right) \leq \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left( \color{Black}{-} \frac { 3 } { 2 } \right) \quad \color{Cerulean} { Reverse\: the\: inequality. } } \\ { x \leq 4 } \end{array}$

Answer:

Interval notation: $(−∞, 4]$

Exercise $\PageIndex{2}$

Solve and graph the solution set: $10 - 5 ( 2 x + 3 ) \leq 25$

Answer

$[ - 3 , \infty )$;

Video Solution: www.youtube.com/v/COLLNtwYFm8

Translation of Linear Inequalities

Some of the key words and phrases that indicate inequalities are summarized below:

Key Phrases	Translation
A number is at least $5$.	$x\geq 5$
A number is $5$ or more inclusive.	$x\geq 5$
A number is at most $3$.	$x\leq 3$
A number is $3$ or less inclusive.	$x\leq 3$
A number is strictly less than $4$.	$x<4$
A number is less than $4$, noninclusive.	$x<4$
A number is greater than $7$.	$x>7$
A number is more than $7$, noninclusive.	$x>7$
A number is in between $2$ and $10$.	$2<x<10$
A number is at least $5$ and at most $15$.	$5\leq x\leq 15$
A number may range from $5$ to $15$.	$5\leq x\leq 15$

Key Takeaways

Inequalities typically have infinitely many solutions. The solutions are presented graphically on a number line or using interval notation or both.
All but one of the rules for solving linear inequalities are the same as solving linear equations. If you divide or multiply an inequality by a negative number, reverse the inequality to obtain an equivalent inequality.

	\( x \geq -3 \)
Shade to the right of \(−3\), and put a bracket at \(−3\).	$.$
Write in interval notation.	\( [-3, \infty) \)

	\( x \leq -\dfrac{3}{5} \)
Shade to the left of \(−\frac{3}{5}\), and put a bracket at \(−\frac{3}{5}\).	$.$
Write in interval notation.	\( \bigg( -\infty, \dfrac{3}{5}\bigg] \)

Key Phrases	Translation
A number is at least \(5\).	\(x\geq 5\)
A number is \(5\) or more inclusive.	\(x\geq 5\)
A number is at most \(3\).	\(x\leq 3\)
A number is \(3\) or less inclusive.	\(x\leq 3\)
A number is strictly less than \(4\).	\(x<4\)
A number is less than \(4\), noninclusive.	\(x<4\)
A number is greater than \(7\).	\(x>7\)
A number is more than \(7\), noninclusive.	\(x>7\)
A number is in between \(2\) and \(10\).	\(2<x<10\)
A number is at least \(5\) and at most \(15\).	\(5\leq x\leq 15\)
A number may range from \(5\) to \(15\).	\(5\leq x\leq 15\)

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\):

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

Example \(\PageIndex{2}\)

Exercise \(\PageIndex{1}\)

Example \(\PageIndex{3}\):

Example \(\PageIndex{4}\):

Example \(\PageIndex{5}\):

Example \(\PageIndex{6}\):

Exercise \(\PageIndex{2}\)

	\( x < 2.5 \)
Shade to the left of 2.5 and put a parenthesis at 2.5.	$.$
Write in interval notation.	\( (-\infty, 2.5) \)

Addition property of equality:	If \(A=B\), then \(A\color{Cerulean}{+c}\color{Black} = B\color{Cerulean}{+c}\)
Subtraction property of equality:	If \(A=B\), then \(A\color{Cerulean}{-c}\color{Black} = B\color{Cerulean}{-c}\)
Multiplication property of equality:	If \(A=B\), then \(\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}\)
Division property of equality:	If \(A=B\), then \(\frac{A}{\color{Cerulean}{c}}\color{Black} = \frac{B}{\color{Cerulean}{c}}, \color{Cerulean}{c}\color{Black} \neq {0}\)

Addition property of inequalities:	If \(A<B\) then, \(A \color{Cerulean}{+c}\:\color{Black}{<}\:B\color{Cerulean}{+c}\)
Subtraction property of inequalities:	If \(A<B\) then, \(A \color{Cerulean}{-c}\:\color{Black}{<}\:B\color{Cerulean}{-c}\)
Multiplication property of inequalities:	If \(A<B\), then \(\color{Cerulean}{c}\color{Black}{A}\:<\:\color{Cerulean}{c}\color{Cerulean}\color{Black}{B}\) If \(A<B\), then \(\color{Cerulean}{-c}\color{Black}{A}\:\color{OliveGreen}{>}\:\color{Cerulean}{-c}\color{Cerulean}\color{Black}{B}\)
Division property of inequalities:	If \(A<B\), then \(\frac{A}{\color{Cerulean}{c}}\color{Black}{<}\frac{B}{\color{Cerulean}{c}}, \color{Cerulean}{c}\color{Black} \neq {0}\) If \(A<B\), then \(\frac{A}{\color{Cerulean}{-c}}\color{OliveGreen}{>}\frac{\color{Black}{B}}{\color{Cerulean}{-c}}, \color{Cerulean}{c}\color{Black} \neq {0}\)