4.4: Quadratic Functions and Applications
- Page ID
- 147268
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Recognize the graph of a quadratic function
- Find the axis of symmetry and vertex of a parabola
- Identify domain and range of quadratic functions
- Solve maximum and minimum applications
- Find the intercepts of a parabola
- Find a break-even point in a quadratic application
Before you get started, take this prerequisite quiz.
1. Sketch a graph of \(y=x^2\). Include at least 3 key points on the graph.
- Click here to check your answer
-

If you missed this problem, review Section 4.2. (Note that this will open in a new window.)
2. If \(f(x)=2x^2-x+1\), find each of the following:
a. \(f(3)\)
b. \(f(-2)\)
- Click here to check your answer
-
a. \(16\)
b. \(11\)
If you missed any part of this problem, review Section 4.1. (Note that this will open in a new window.)
3. Identify the domain and range of the function graphed here.

- Click here to check your answer
-
Domain: \((-\infty, \infty)\)
Range: \((-\infty, 4]\)
If you missed any part of this problem, review Section 4.1. (Note that this will open in a new window.)
Recognize the Graph of a Quadratic Function
Previously we very briefly looked at the function \(f(x)=x^{2}\), which we called the square function. It was one of the first non-linear functions we looked at. Now we will graph functions of the form \(f(x)=a x^{2}+b x+c\) if \(a \neq 0\). We call this kind of function a quadratic function.
A quadratic function, where \(a, b\), and \(c\) are real numbers and \(a≠0\), is a function of the form
\(f(x)=a x^{2}+b x+c\)
We graphed the quadratic function \(f(x)=x^{2}\) by plotting points.
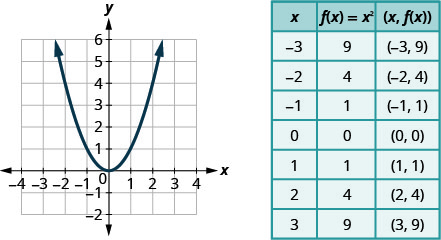
Every quadratic function has a graph that looks like this. We call this figure a parabola. Let’s practice graphing a parabola by plotting a few points.
Graph: \(f(x)=x^{2}-1\).
Solution:
We will graph the function by plotting points.
|
Choose integer values for \(x\), |
 |
| Plot the points, and then connect them with a smooth curve. The result will be the graph of the function \(f(x)=x^{2}-1\). |
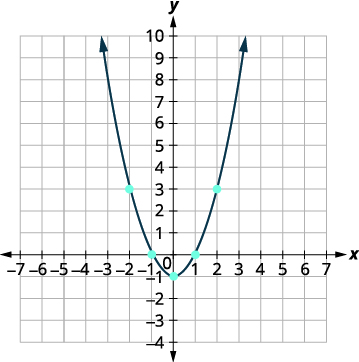 |
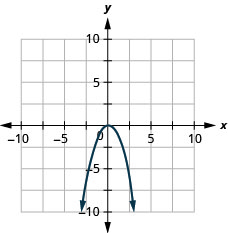
Graph \(f(x)=-x^{2}\).
- Answer
-
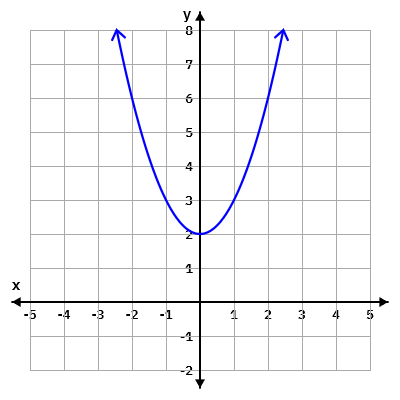
Graph \(f(x)=x^{2}+2\).
- Answer
-
All graphs of quadratic functions of the form \(f(x)=a x^{2}+b x+c\) are parabolas that open upward or downward.
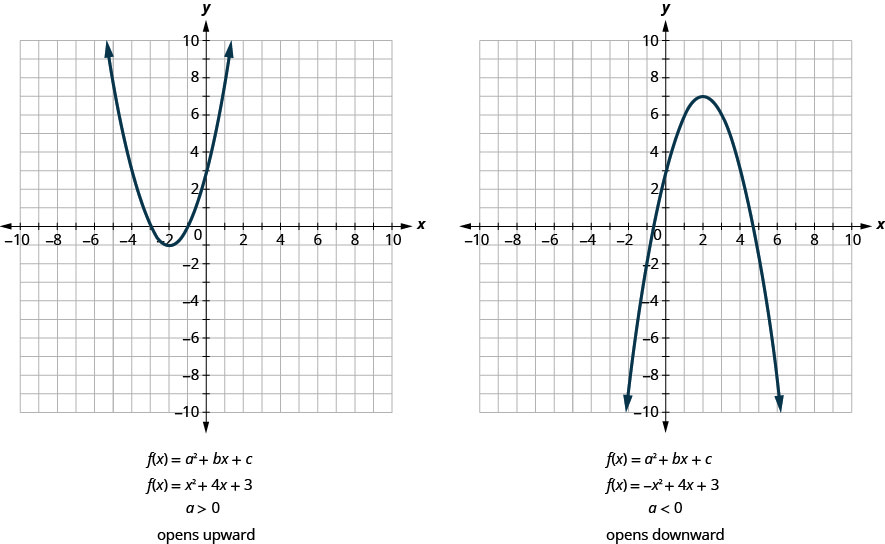
Notice that the only difference in the two equations is the negative sign in the quadratic term \(ax^{2}\). The negative in front of the \(ax^{2}\) indicates a vertical reflection and flips the parabola upside-down. Therefore when the quadratic term \(ax^{2}\) is positive, the parabola opens upward. When the quadratic term \(ax^{2}\) is negative, the parabola opens downward.
Parabola Orientation
For the graph of the quadratic function \(f(x)=a x^{2}+b x+c\):
- If \(a>0\), the parabola opens upward.

- If \(a<0\), the parabola includes a vertical reflection causing the parabola to open downward.

Without graphing, determine whether each parabola opens upward or downward:
- \(f(x)=-3 x^{2}+2 x-4\)
- \(f(x)=6 x^{2}+7 x-9\)
Solution:
a. Find the value of \(a\).
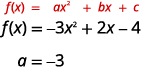
Since the \(a\) is negative, the parabola will open downward.
b. Find the value of \(a\).
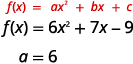
Since the \(a\) is positive, the parabola will open upward.
Without graphing, determine whether the graph of each function is a parabola that opens upward or downward:
- \(f(x)=2 x^{2}+5 x-2\)
- \(f(x)=-3 x^{2}-4 x+7\)
- Answer
-
- up
- down
Without graphing, determine whether the graph of each function is a parabola that opens upward or downward:
- \(f(x)=-2 x^{2}-2 x-3\)
- \(f(x)=5 x^{2}-2 x-1\)
- Answer
-
- down
- up
Finding the Axis of Symmetry and Vertex of a Parabola
Look again at Figure 9.6.10. Do you see that we could fold each parabola in half and then one side would lie on top of the other? The ‘fold line’ is a line of symmetry. We call it the axis of symmetry of the parabola.
We show the same two graphs again with the axis of symmetry.
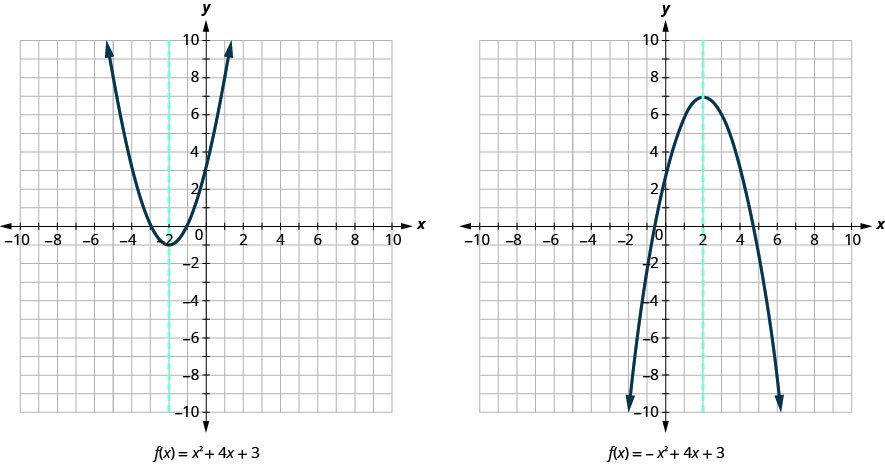
The axis of symmetry can be found fairly directly using an algebraic formula. This formula can be derived by using the Quadratic Formula. We will omit the derivation here and proceed directly to using the result.
The equation of the axis of symmetry of the graph of \(f(x)=a x^{2}+b x+c\) is \(x=-\frac{b}{2 a}\). This equation allows us to find the axis of symmetry directly from the equation without even needing to see the graph.
So to find the equation of symmetry of each of the parabolas we graphed above, we will substitute \(a\) and \(b\) into the formula \(x=-\frac{b}{2 a}\).
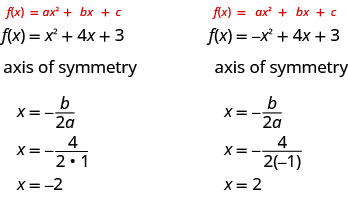
Notice that these are the equations of the dashed blue lines on the graphs.
The point on the parabola that is the lowest (parabola opens up), or the highest (parabola opens down), lies on the axis of symmetry. This point is called the vertex of the parabola.
We can easily find the coordinates of the vertex, because we know it is on the axis of symmetry. This means its
\(x\)-coordinate is \(-\frac{b}{2 a}\). To find the \(y\)-coordinate of the vertex we substitute the value of the \(x\)-coordinate into the quadratic function.
The graph of the function \(f(x)=a x^{2}+b x+c\) is a parabola where:
- the axis of symmetry is the vertical line \(x=-\frac{b}{2 a}\).
- the vertex is a point on the axis of symmetry, so its \(x\)-coordinate is \(-\frac{b}{2 a}\)
- the \(y\)-coordinate of the vertex is found by substituting \(x=-\frac{b}{2 a}\) into the quadratic function.
For the graph of \(f(x)=4 x^{2}-16 x+5\) algebraically find:
- the axis of symmetry
- the vertex
Solution:
a.
|
\(f(x)=ax^{2}+bx+c\) \(f(x)=4 x^{2}-16 x+5\) |
|
| The axis of symmetry is the vertical line \(x=-\frac{b}{2 a}\). | |
| Substitute the values \(a,b\) into the equation. | \(x=-\frac{-16}{2 \cdot 4}\) |
| Simplify. | \(x=2\) |
| The axis of symmetry is the line \(x=2\). |
b.
| \(f(x)=4 x^{2}-16 x+5\) | |
| The vertex is a point on the line of symmetry, so its \(x\)-coordinate will be \(x=2\). Find \(f(2)\). | \(f(x)=4(2)^{2}-16(2)+5\) |
| Simplify. | \(f(x)=4(4)-16(2)+5\) |
| The result is the \(y\)-coordinate. | \(f(2)=-11\) |
| The vertex is \((2,-11)\). |
For the graph of \(f(x)=2 x^{2}-4 x-3\) algebraically find:
- the axis of symmetry
- the vertex
- Answer
-
- \(x=1\)
- \((1,-5)\)
For the graph of \(f(x)=-3 x^{2}-18 x-6\) algebraically find:
- the axis of symmetry
- the vertex
- Answer
-
- \(x=-3\)
- \((-3,21)\)
The axis of symmetry and the vertex can also be found on Desmos.
The vertex will be the turning point of the parabola, which is also the lowest (parabola opens up), or the highest (parabola opens down) point on the function. The axis of symmetry will be the vertical line that includes that vertex.
For the graph of \(f(x)= x^{2}+6 x-1\) use Desmos to find:
- the vertex
- the axis of symmetry
Solution:
a. Begin by graphing the function, and finding the turning point. This turning point is the vertex. The vertex in this problem is (-3,-10).

b. The axis of symmetry is the vertical line that includes the vertex. As every vertical line is written in the form \(x=a\), this will always be the \(x\)-value of the vertex. In this problem, the axis of symmetry is \(x=-3\).

Note that the axis of symmetry won't be shown on Desmos unless you create it as an additional function.
For the graph of \(f(x)=-2 x^{2}+4 x+3\) use Desmos to find:
- the vertex
- the axis of symmetry
- Answer
-
- \((1,5)\)
- \(x=1\)
Domain and Range of a Parabola
The graph of each parabola continues forever to the left and right. This means that the domain of any function in the form \(f(x)=a x^{2}+b x+c\) will be \((-\infty,\infty)\).
The range, however, will depend on the \(a\)-value and the vertex.
For the graph shown below, identify the domain and range.
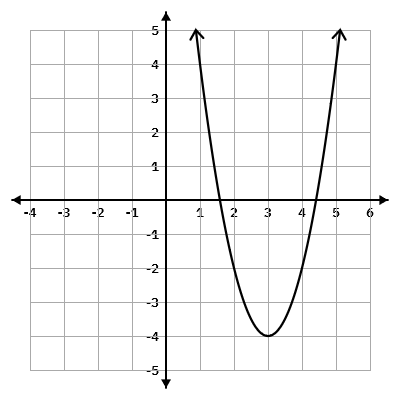
The domain of any function is all the possible \(x\)-values. Since a parabola continues forever to the left and right, the domain will be \((-\infty,\infty)\).
The range of any function is all the possible \(y\)-values. This function includes all \(y\)-values above the vertex, but none below the vertex. The vertex includes the minimum \(y\)-value of -4. Therefore the range of this function is \([-4,\infty)\). Note the \([\)bracket\(]\) on the -4 since that point is included on the graph.
For the graph shown below, identify the domain and range.

The domain of any function is all the possible \(x\)-values. Since a parabola continues forever to the left and right, the domain will be \((-\infty,\infty)\).
The range of any function is all the possible \(y\)-values. This function includes all \(y\)-values below the vertex, but none above the vertex. The vertex includes the maximum \(y\)-value of 3. Therefore the range of this function is \((-\infty, 3]\). Note the \([\)bracket\(]\) on the 3 since that point is included on the graph.
Note that the range of the function depends on the vertex as well as the \(a\)-value of the function. If \(a>0\), then the y-values will include the y-value of the vertex and everything higher. It will be expressed as \([f(-\frac{b}{2 a}),\infty)\). If \(a<0\), then the y-values will include everything lower than the maximum value, up to and including the maximum value. It will be expressed as \((-\infty,f(-\frac{b}{2 a})]\).
Applications of the Vertex, Domain, and Range of a Parabola
The vertex, domain, and range of a parabola have many applications. Since the vertex represents the highest or lowest point of the parabola, this can help us identify maximum or minimum outcomes of a quadratic application. For example, businesses may want to find their maximum profit or minimum cost.
In many applications, negative inputs and/or outputs do not apply. Rather than looking at the algebraic domain and range, we look at practical domain and practical range as the set of values that make sense in the given scenario.
For example, if \(x\) represents the number of items manufactured, it would not be practical to include any negative \(x\)-values. Much like linear programming from Section 4.3, we will only allow for \(x\)-values where \(x \geq 0\).
The output values may or may not be negative. If \(y\) represents profit, for example, it IS possible for a company to have a negative profit. If \(y\) represents revenue however, it is NOT possible for a company to have a negative revenue.
A company that sells televisions has found their revenue to be determined by \(R(t)=-50t^{2}+2000t\), where \(t\) is the number of televisions sold.
- Find the value of \(t\) that will produce the maximum revenue.
- What is the maximum revenue?
- What is the practical range?
- What is the practical domain?
Solution:
\(R(t)=-50t^{2}+2000t\)
Note that in this equation:
- \(t\) is the input and represents the number of televisions sold. This would be represented by the \(x\)-axis of the graph.
- \(R(t)\) is the output and represents the revenue. This would be represented by the \(y\)-axis of the graph.
a. Find the equation of the axis of symmetry.
\(\begin{array}{l}{t=-\frac{b}{2 a}} \\ {t=-\frac{2000}{2(-50)}} \\ {t=20}\end{array}\)
The equation of the axis of symmetry is \(t=20\).
The vertex is on the line \(t=20\).
The maximum revenue occurs when \(t=20\) televisions.
b. To find the maximum revenue, find \(R(20)\).
\(\begin{array}{l}{R(t)=-50 t^{2}+2000 t} \\ {R(t)=-50(20)^{2}+2000(20)}\end{array}\)
Use a calculator to simplify.
\(R(t)=20000\)
The vertex is \((20, 20000)\).
When the company sells \(20\) televisions, they will have a revenue of $\(20,000\).
c. To find the practical range, we need to consider that the output values represent revenue, which cannot be negative. Therefore the practical range would be all \(y\)-values from zero up to the maximum, or \([0, 20000]\).
d. The practical domain would be all the input values that are included in the practical range above. We'll look at the algebraic method to find this in the examples below. For now, we can read these values from the graph of the function.

We can see that any \(x\)-value over 40 televisions would result in a negative revenue. Therefore the practical domain is \([0, 40]\).
A bakery has found their profit to be determined by \(P(c)=-0.5c^{2}+96c-3047\), where \(c\) is the number of cupcakes baked each day.
- Find the value of \(c\) that will produce the maximum profit.
- What is the maximum profit?
- Answer
-
The bakery will earn a maximum profit of $\(1561\) if \(96\) cupcakes are baked each day.
Find the Intercepts of a Parabola
When we graphed linear equations, we often used the \(x\)- and \(y\)-intercepts to help us graph the lines. Finding the coordinates of the intercepts will help us to graph parabolas, too.
Remember, at the \(y\)-intercept the value of \(x\) is zero. So to find the \(y\)-intercept, we substitute \(x=0\) into the function. Likewise, at the \(x\)-intercepts the value of \(y\) is zero. So to find the \(x\)-intercept, we substitute \(y=0\) into the function.
To find the intercepts of a parabola whose function is \(f(x)=a x^{2}+b x+c\):
- \(y\)-intercept: Let \(x=0\) and solve for \(f(x)\).
- \(x\)-intercepts: Let \(f(x)=0\) and solve for \(x\).
- An \(x\)-intercept results when the value of \(f(x)\) is zero. To find an \(x\)-intercept, we let \(f(x)=0\). In other words, we will need to solve the equation \(0=a x^{2}+b x+c\) for \(x\). While several methods exist to solve quadratic equations like this, we will rely on the quadratic formula for the purposes of this course.
The quadratic formula states that if \(ax^{2}+bx+c=0\) and \(a \ne 0\),
then \(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\), provided that \(b^{2}-4ac \ge 0\)
Find the intercepts of the parabola whose function is \(f(x)=x^{2}-2 x-8\).
Solution:
| To find the \(y\)-intercept, let \(x=0\) and solve for \(f(x)\). | \(f(x)=x^{2}-2 x-8\) |
| \(f(0)=\color{red}0\color{black}^{2}-2 \cdot \color{red}0 \color{black}-8\) | |
| \(f(0)=-8\) | |
| When \(x=0\), then \(f(0)=-8\). The \(y\)-intercept is the point \((0,-8)\). | |
| To find the \(x\)-intercept, let \(f(x)=0\) and solve for \(x\). | \(f(x)=x^{2}-2 x-8\) |
| \(0=x^{2}-2 x-8\) | |
| Use the Quadratic Formula to solve for \(x\). | \(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) |
| \(a=1, b=-2, c=-8\) | \(x=\frac{2 \pm \sqrt{(-2)^{2}-4(1)(-8)}}{2(1)}\) |
| Simplify. | \(x=\frac{2 \pm \sqrt{36}}{2}\) |
| \(x=\frac{2 \pm 6}{2}\) | |
| \(x=1 \pm 3\) | |
| \(x=4\) or \(x=-2\) | |
| When \(f(x)=0\), then \(x=4\) or \(x=-2\). The \(x\)-intercepts are the points \((4,0)\) and \((-2,0)\). |
Find the intercepts of the parabola whose function is \(f(x)=x^{2}-4 x-12\).
- Answer
-
\(y\) -intercept: \((0,-12) x\) -intercepts \((-2,0),(6,0)\)
For the purposes of this course, we can also use Desmos to identify the intercepts of the function.
Find the intercepts of the parabola whose function is \(f(x)=x^{2}-5x-6\).
Solution:

The x-intercepts are \((-1,0)\) and \((6,0)\).
The y-intercept is \(0,-6)\).
Note that in many cases, the intercepts are not rational numbers. This is ok!
Find the intercepts of the parabola whose function is \(f(x)=-2x^{2}-9x+14\).
Solution:

The x-intercepts are \((-5.723,0)\) and \((1.223,0)\).
The y-intercept is \(0,14)\).
Finding the Break-Even Points
Intercepts also have many business applications. Remember that an x-intercept is the value of x when the function equals zero. The point at which revenue and cost are equal is known as the break-even point. This is also where the profit equals zero.
The television company from example 7 has found their profit to be determined by \(P(t)=-50t^{2}+1500t-4000\), where \(t\) is the number of televisions sold.
- Find the break-even points, rounding to the nearest whole number if necessary.
- What range of television sales will result in a profit? A loss?
- What does the y-intercept represent?
Solution:
\(P(t)=-50t^{2}+1500t-4000\)
a. The break-even points exist when the profit is $\(0\). On the parabola, this exists when y is zero, or at the x-intercepts. Substitute \(0\) in for \(P(t)\).
\(P(t)=-50t^{2}+1500t-4000\)
\(0=-50t^{2}+1500t-4000\)
Use the quadratic formula to solve for \(t\).
\(t=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
\(t=\frac{-1500 \pm \sqrt{(1500)^{2}-4 (-50)(-4000)}}{2 (-50)}\)
\(t=\frac{-1500 \pm \sqrt{1450000}}{-100}\)
\(t \approx \frac{-1500 \pm 1204.2}{-100}\)
\(t \approx \frac{-295.8}{-100}\) or \(t \approx \frac{-2704.2}{-100}\)
\(t \approx 2.958\) or \(t \approx 27.042\)
The x-intercepts of the parabola are approximately \((0, 3)\) and \((0, 27)\).
The company will break even, or make a profit of $\(0\), when either \(3\) or \(27\) televisions are sold.

b. Since the \(a\) value of the function is negative, the parabola will open downward. This means that the profit will be positive between the two x-intercepts and will be negative outside of the x-intercepts.
The company will make a profit by selling more than \(3\) and less than \(27\) televisions.
The company have a negative profit, or will lose money, by selling less than than \(3\) or more than \(27\) televisions.
c. The y-intercept is \((0, -4000)\). If the company sells \(0\) televisions, it will have a profit of \(-$4,000\).
The bakery from exercise 8 has found their profit to be determined by \(P(c)=-0.5c^{2}+96c-3047\), where \(c\) is the number of cupcakes baked each day.
- Find the break-even points, rounding to the nearest whole number if necessary.
- What range of cupcake production will result in a profit? A loss?
- What does the y-intercept represent?
- Answer
-
- The break-even points occur if the bakery makes \(40\) or \(152\) cupcakes each day.
- The bakery will earn a profit if it bakes more than \(40\) and less than \(152\) cupcakes each day; it will lose money if it bakes less than \(40\) or more than \(152\) cupcakes each day.
- If the bakery does not bake any cupcakes, it will have a profit of \(-$3,047\) that day.

Key Concepts
- Parabola Orientation
- For the graph of the quadratic function \(f(x)=a x^{2}+b x+c\), if
- \(a>0\), the parabola opens upward.
- \(a<0\), the parabola opens downward.
- For the graph of the quadratic function \(f(x)=a x^{2}+b x+c\), if
- Axis of Symmetry and Vertex of a Parabola The graph of the function \(f(x)=a x^{2}+b x+c\) is a parabola where:
- the axis of symmetry is the vertical line \(x=-\frac{b}{2 a}\).
- the vertex is a point on the axis of symmetry, so its \(x\)-coordinate is \(-\frac{b}{2 a}\).
- the \(y\)-coordinate of the vertex is found by substituting \(x=-\frac{b}{2 a}\) into the quadratic equation.
- Find the Intercepts of a Parabola
- To find the intercepts of a parabola whose function is \(f(x)=a x^{2}+b x+c\):
- \(y\)-intercept
- Let \(x=0\) and solve for \(f(x)\).
- \(x\)-intercepts
- Let \(f(x)=0\) and solve for \(x\).
- \(y\)-intercept
- To find the intercepts of a parabola whose function is \(f(x)=a x^{2}+b x+c\):
- Minimum or Maximum Values of a Quadratic Equation
- The \(y\)-coordinate of the vertex of the graph of a quadratic equation is the
- minimum value of the quadratic equation if the parabola opens upward.
- maximum value of the quadratic equation if the parabola opens downward.
Glossary
- quadratic function
- A quadratic function, where \(a, b\), and \(c\) are real numbers and \(a≠0\), is a function of the form \(f(x)=ax^{2}+bx+c\).

