4.1E: Exercises

Exercises

In Exercises 1 - 18, for the given rational function \(f\):

• Find the domain of \(f\).
• Identify any vertical asymptotes of the graph of \(y = f(x)\).
• Identify any holes in the graph.
• Find the horizontal asymptote, if it exists.
• Find the slant asymptote, if it exists.
• Graph the function using a graphing utility and describe the behavior near the asymptotes.

1. \(f(x) = \dfrac{x}{3x - 6}\)
2. \(f(x) = \dfrac{3 + 7x}{5 - 2x}\)
3. \(f(x) = \dfrac{x}{x^{2} + x - 12}\)
4. \(f(x) = \dfrac{x}{x^{2} + 1}\)
5. \(f(x) = \dfrac{x + 7}{(x + 3)^{2}}\)
6. \(f(x) = \dfrac{x^{3} + 1}{x^{2} - 1}\)
7. \(f(x) = \dfrac{4x}{x^2+4}\)
8. \(f(x) = \dfrac{4x}{x^2-4}\)
9. \(f(x) = \dfrac{x^2-x-12}{x^2+x-6}\)
10. \(f(x) = \dfrac{3x^2-5x-2}{x^2-9}\)
11. \(f(x) = \dfrac{x^3+2x^2+x}{x^2-x-2}\)
12. \(f(x) = \dfrac{x^{3} - 3x + 1}{x^{2} + 1}\)
13. \(f(x) = \dfrac{2x^{2} + 5x - 3}{3x + 2}\)
14. \(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}\)
15. \(f(x) = \dfrac{-5x^{4} - 3x^{3} + x^{2} - 10}{x^{3} - 3x^{2} + 3x - 1}\)
16. \(f(x) = \dfrac{x^3}{1-x}\)
17. \(f(x) = \dfrac{18-2x^2}{x^2-9}\)
18. \(f(x) = \dfrac{x^3-4x^2-4x-5}{x^2+x+1}\) [alltheasymplast]
19. The cost \(C\) in dollars to remove \(p\)% of the invasive species of Ippizuti fish from Sasquatch Pond is given by \[C(p) = \frac{1770p}{100 - p}, \quad 0 \leq p < 100 \nonumber\]
    1. Find and interpret \(C(25)\) and \(C(95)\).
    2. What does the vertical asymptote at \(x = 100\) mean within the context of the problem?
    3. What percentage of the Ippizuti fish can you remove for $40000?
20. In the Exercises for Section 1.4, the population of Sasquatch in Portage County was modeled by the function \[P(t) = \frac{150t}{t + 15},\nonumber\] where \(t = 0\) represents the year 1803. Find the horizontal asymptote of the graph of \(y = P(t)\) and explain what it means.
21. Recall from Example 1.5.3 that the cost \(C\) (in dollars) to make \(x\) dOpi media players is \(C(x) = 100x+2000\), \(x \geq 0\).
    1. Find a formula for the average cost \(\overline{C}(x)\). Recall: \(\overline{C}(x) = \frac{C(x)}{x}\).
    2. Find and interpret \(\overline{C}(1)\) and \(\overline{C}(100)\).
    3. How many dOpis need to be produced so that the average cost per dOpi is \(\$ 200\)?
    4. Interpret the behavior of \(\overline{C}(x)\) as \(x \rightarrow 0^{+}\). (HINT: You may want to find the fixed cost \(C(0)\) to help in your interpretation.)
    5. Interpret the behavior of \(\overline{C}(x)\) as \(x \rightarrow \infty\). (HINT: You may want to find the variable cost (defined in Example 2.1.5 in Section 2.1) to help in your interpretation.)
22. In Exercise 35 in Section 3.1, we fit a few polynomial models to the following electric circuit data. (The circuit was built with a variable resistor. For each of the following resistance values (measured in kilo-ohms, \(k \Omega\)), the corresponding power to the load (measured in milliwatts, \(mW\)) is given in the table below.)

    Resistance: (\(k \Omega\))	1.012	2.199	3.275	4.676	6.805	9.975
    Power: (\(mW\))	1.063	1.496	1.610	1.613	1.505	1.314

    Using some fundamental laws of circuit analysis mixed with a healthy dose of algebra, we can derive the actual formula relating power to resistance. For this circuit, it is \(P(x) = \frac{25x}{(x + 3.9)^2}\), where \(x\) is the resistance value, \(x \geq 0\).

    1. Graph the data along with the function \(y = P(x)\) on your calculator.
    2. Use your calculator to approximate the maximum power that can be delivered to the load. What is the corresponding resistance value?
    3. Find and interpret the end behavior of \(P(x)\) as \(x \rightarrow \infty\).
23. In his now famous 1919 dissertation The Learning Curve Equation, Louis Leon Thurstone presents a rational function which models the number of words a person can type in four minutes as a function of the number of pages of practice one has completed. (This paper, which is now in the public domain and can be found here, is from a bygone era when students at business schools took typing classes on manual typewriters.) Using his original notation and original language, we have \(Y = \frac{L(X + P)}{(X + P) + R}\) where \(L\) is the predicted practice limit in terms of speed units, \(X\) is pages written, \(Y\) is writing speed in terms of words in four minutes, \(P\) is equivalent previous practice in terms of pages and \(R\) is the rate of learning. In Figure 5 of the paper, he graphs a scatter plot and the curve \(Y = \frac{216(X + 19)}{X + 148}\). Discuss this equation with your classmates. How would you update the notation? Explain what the horizontal asymptote of the graph means. You should take some time to look at the original paper. Skip over the computations you don’t understand yet and try to get a sense of the time and place in which the study was conducted.

Answers

1. \(f(x) = \dfrac{x}{3x - 6}\)
   Domain: \((-\infty, 2) \cup (2, \infty)\)
   Vertical asymptote: \(x = 2\)
   As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\)
   As \(x \rightarrow 2^{+}, f(x) \rightarrow \infty\)
   No holes in the graph
   Horizontal asymptote: \(y = \frac{1}{3}\)
   As \(x \rightarrow -\infty, f(x) \rightarrow \frac{1}{3}^{-}\)
   As \(x \rightarrow \infty, f(x) \rightarrow \frac{1}{3}^{+}\)

2. \(f(x) = \dfrac{3 + 7x}{5 - 2x}\)
   Domain: \((-\infty, \frac{5}{2}) \cup (\frac{5}{2}, \infty)\)
   Vertical asymptote: \(x = \frac{5}{2}\)
   As \(x \rightarrow \frac{5}{2}^{-}, f(x) \rightarrow \infty\)
   As \(x \rightarrow \frac{5}{2}^{+}, f(x) \rightarrow -\infty\)
   No holes in the graph
   Horizontal asymptote: \(y = -\frac{7}{2}\)
   As \(x \rightarrow -\infty, f(x) \rightarrow -\frac{7}{2}^{+}\)
   As \(x \rightarrow \infty, f(x) \rightarrow -\frac{7}{2}^{-}\)

3. \(f(x) = \dfrac{x}{x^{2} + x - 12} = \dfrac{x}{(x + 4)(x - 3)}\)
   Domain: \((-\infty, -4) \cup (-4, 3) \cup (3, \infty)\)
   Vertical asymptotes: \(x = -4, x = 3\)
   As \(x \rightarrow -4^{-}, f(x) \rightarrow -\infty\)
   As \(x \rightarrow -4^{+}, f(x) \rightarrow \infty\)
   As \(x \rightarrow 3^{-}, f(x) \rightarrow -\infty\)
   As \(x \rightarrow 3^{+}, f(x) \rightarrow \infty\)
   No holes in the graph
   Horizontal asymptote: \(y = 0\)
   As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
   As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)

4. \(f(x) = \dfrac{x}{x^{2} + 1}\)
   Domain: \((-\infty, \infty)\)
   No vertical asymptotes
   No holes in the graph
   Horizontal asymptote: \(y = 0\)
   As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
   As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)

5. \(f(x) = \dfrac{x + 7}{(x + 3)^{2}}\)
   Domain: \((-\infty, -3) \cup (-3, \infty)\)
   Vertical asymptote: \(x = -3\)
   As \(x \rightarrow -3^{-}, f(x) \rightarrow \infty\)
   As \(x \rightarrow -3^{+}, f(x) \rightarrow \infty\)
   No holes in the graph
   Horizontal asymptote: \(y = 0\)
   ¹⁹As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
   As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)

6. \(f(x) = \dfrac{x^{3} + 1}{x^{2} - 1} = \dfrac{x^{2} - x+ 1}{x-1}\)
   Domain: \((-\infty, -1) \cup (-1, 1) \cup (1, \infty)\)
   Vertical asymptote: \(x = 1\)
   As \(x \rightarrow 1^{-}, f(x) \rightarrow -\infty\)
   As \(x \rightarrow 1^{+}, f(x) \rightarrow \infty\)
   Hole at \((-1, -\frac{3}{2})\)
   Slant asymptote: \(y=x\)
   As \(x \rightarrow -\infty\), the graph is below \(y=x\)
   As \(x \rightarrow \infty\), the graph is above \(y=x\)

7. \(f(x) = \dfrac{4x}{x^{2} + 4}\)
   Domain: \((-\infty, \infty)\)
   No vertical asymptotes
   No holes in the graph
   Horizontal asymptote: \(y = 0\)
   As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
   As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)

8. \(f(x) = \dfrac{4x}{x^{2} -4} = \dfrac{4x}{(x + 2)(x - 2)}\)
   Domain: \((-\infty, -2) \cup (-2, 2) \cup (2, \infty)\)
   Vertical asymptotes: \(x = -2, x = 2\)
   As \(x \rightarrow -2^{-}, f(x) \rightarrow -\infty\)
   As \(x \rightarrow -2^{+}, f(x) \rightarrow \infty\)
   As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\)
   As \(x \rightarrow 2^{+}, f(x) \rightarrow \infty\)
   No holes in the graph
   Horizontal asymptote: \(y = 0\)
   As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
   As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)

9. \(f(x) = \dfrac{x^2-x-12}{x^{2} +x - 6} = \dfrac{x-4}{x - 2}\)
   Domain: \((-\infty, -3) \cup (-3, 2) \cup (2, \infty)\)
   Vertical asymptote: \(x = 2\)
   As \(x \rightarrow 2^{-}, f(x) \rightarrow \infty\)
   As \(x \rightarrow 2^{+}, f(x) \rightarrow -\infty\)
   Hole at \(\left(-3, \frac{7}{5} \right)\)
   Horizontal asymptote: \(y = 1\)
   As \(x \rightarrow -\infty, f(x) \rightarrow 1^{+}\)
   As \(x \rightarrow \infty, f(x) \rightarrow 1^{-}\)

10. \(f(x) = \dfrac{3x^2-5x-2}{x^{2} -9} = \dfrac{(3x+1)(x-2)}{(x + 3)(x - 3)}\)
    Domain: \((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\)
    Vertical asymptotes: \(x = -3, x = 3\)
    As \(x \rightarrow -3^{-}, f(x) \rightarrow \infty\)
    As \(x \rightarrow -3^{+}, f(x) \rightarrow -\infty\)
    As \(x \rightarrow 3^{-}, f(x) \rightarrow -\infty\)
    As \(x \rightarrow 3^{+}, f(x) \rightarrow \infty\)
    No holes in the graph
    Horizontal asymptote: \(y = 3\)
    As \(x \rightarrow -\infty, f(x) \rightarrow 3^{+}\)
    As \(x \rightarrow \infty, f(x) \rightarrow 3^{-}\)

11. \(f(x) = \dfrac{x^3+2x^2+x}{x^{2} -x-2} = \dfrac{x(x+1)}{x - 2}\)
    Domain: \((-\infty, -1) \cup (-1, 2) \cup (2, \infty)\)
    Vertical asymptote: \(x = 2\)
    As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\)
    As \(x \rightarrow 2^{+}, f(x) \rightarrow \infty\)
    Hole at \((-1,0)\)
    Slant asymptote: \(y=x+3\)
    As \(x \rightarrow -\infty\), the graph is below \(y=x+3\)
    As \(x \rightarrow \infty\), the graph is above \(y=x+3\)

12. \(f(x) = \dfrac{x^3-3x+1}{x^2+1}\)
    Domain: \((-\infty, \infty)\)
    No vertical asymptotes
    No holes in the graph
    Slant asymptote: \(y=x\)
    As \(x \rightarrow -\infty\), the graph is above \(y=x\)
    As \(x \rightarrow \infty\), the graph is below \(y=x\)

13. \(f(x) = \dfrac{2x^{2} + 5x - 3}{3x + 2}\)
    Domain: \(\left(-\infty, -\frac{2}{3}\right) \cup \left(-\frac{2}{3}, \infty\right)\)
    Vertical asymptote: \(x = -\frac{2}{3}\)
    As \(x \rightarrow -\frac{2}{3}^{-}, f(x) \rightarrow \infty\)
    As \(x \rightarrow -\frac{2}{3}^{+}, f(x) \rightarrow -\infty\)
    No holes in the graph
    Slant asymptote: \(y = \frac{2}{3}x + \frac{11}{9}\)
    As \(x \rightarrow -\infty\), the graph is above \(y = \frac{2}{3}x + \frac{11}{9}\)
    As \(x \rightarrow \infty\), the graph is below \(y = \frac{2}{3}x + \frac{11}{9}\)

14. \(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9} = \dfrac{-x^{3} + 4x}{(x-3)(x+3)}\)
    Domain: \((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\)
    Vertical asymptotes: \(x = -3\), \(x=3\)
    As \(x \rightarrow -3^{-}, f(x) \rightarrow \infty\)
    As \(x \rightarrow -3^{+}, f(x) \rightarrow -\infty\)
    As \(x \rightarrow 3^{-}, f(x) \rightarrow \infty\)
    As \(x \rightarrow 3^{+}, f(x) \rightarrow -\infty\)
    No holes in the graph
    Slant asymptote: \(y=-x\)
    As \(x \rightarrow -\infty\), the graph is above \(y=-x\)
    As \(x \rightarrow \infty\), the graph is below \(y=-x\)

15. \(f(x) = \dfrac{-5x^{4} - 3x^{3} + x^{2} - 10}{x^{3} - 3x^{2} + 3x - 1} \\ \phantom{f(x)} = \dfrac{-5x^{4} - 3x^{3} + x^{2} - 10}{(x-1)^3}\)
    Domain: \((-\infty, 1) \cup (1, \infty)\)
    Vertical asymptotes: \(x = 1\)
    As \(x \rightarrow 1^{-}, f(x) \rightarrow \infty\)
    As \(x \rightarrow 1^{+}, f(x) \rightarrow -\infty\)
    No holes in the graph
    Slant asymptote: \(y=-5x-18\)
    As \(x \rightarrow -\infty\), the graph is above \(y=-5x-18\)
    As \(x \rightarrow \infty\), the graph is below \(y=-5x-18\)

16. \(f(x) = \dfrac{x^3}{1-x}\)
    Domain: \((-\infty, 1) \cup (1, \infty)\)
    Vertical asymptote: \(x=1\)
    As \(x \rightarrow 1^{-}, f(x) \rightarrow \infty\)
    As \(x \rightarrow 1^{+}, f(x) \rightarrow -\infty\)
    No holes in the graph
    No horizontal or slant asymptote
    As \(x \rightarrow -\infty\), \(f(x) \rightarrow -\infty\)
    As \(x \rightarrow \infty\), \(f(x) \rightarrow -\infty\)

17. \(f(x) = \dfrac{18-2x^2}{x^2-9} = -2\)
    Domain: \((-\infty, -3) \cup (-3,3) \cup (3, \infty)\)
    No vertical asymptotes
    Holes in the graph at \((-3,-2)\) and \((3,-2)\)
    Horizontal asymptote \(y = -2\)
    As \(x \rightarrow \pm \infty\), \(f(x) = -2\)

18. \(f(x) = \dfrac{x^3-4x^2-4x-5}{x^2+x+1} = x-5\)
    Domain: \((-\infty, \infty)\)
    No vertical asymptotes
    No holes in the graph
    Slant asymptote: \(y = x-5\)
    \(f(x) = x-5\) everywhere.

19. 1. \(C(25) = 590\) means it costs $590 to remove 25% of the fish and and \(C(95)= 33630\) means it would cost $33630 to remove 95% of the fish from the pond.
    2. The vertical asymptote at \(x = 100\) means that as we try to remove 100% of the fish from the pond, the cost increases without bound; i.e., it’s impossible to remove all of the fish.
    3. For $40000 you could remove about 95.76% of the fish.
20. The horizontal asymptote of the graph of \(P(t) = \frac{150t}{t + 15}\) is \(y = 150\) and it means that the model predicts the population of Sasquatch in Portage County will never exceed 150.
21. 1. \(\overline{C}(x) = \frac{100x+2000}{x}\), \(x > 0\).
    2. \(\overline{C}(1) = 2100\) and \(\overline{C}(100) = 120\). When just \(1\) dOpi is produced, the cost per dOpi is \(\$2100\), but when \(100\) dOpis are produced, the cost per dOpi is \(\$120\).
    3. \(\overline{C}(x) = 200\) when \(x = 20\). So to get the cost per dOpi to \(\$200\), \(20\) dOpis need to be produced.
    4. As \(x \rightarrow 0^{+}\), \(\overline{C}(x) \rightarrow \infty\). This means that as fewer and fewer dOpis are produced, the cost per dOpi becomes unbounded. In this situation, there is a fixed cost of \(\$2000\) (\(C(0) = 2000\)), we are trying to spread that \(\$2000\) over fewer and fewer dOpis.
    5. As \(x \rightarrow \infty\), \(\overline{C}(x) \rightarrow 100^{+}\). This means that as more and more dOpis are produced, the cost per dOpi approaches \(\$100\), but is always a little more than \(\$100\). Since \(\$100\) is the variable cost per dOpi (\(C(x) = \underline{100}x+2000\)), it means that no matter how many dOpis are produced, the average cost per dOpi will always be a bit higher than the variable cost to produce a dOpi. As before, we can attribute this to the \(\$2000\) fixed cost, which factors into the average cost per dOpi no matter how many dOpis are produced.
22. 1. 
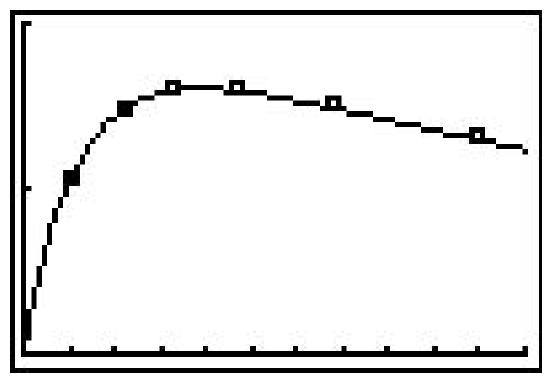
    2. The maximum power is approximately \(1.603 \; mW\) which corresponds to \(3.9 \; k\Omega\).
    3. As \(x \rightarrow \infty, \; P(x) \rightarrow 0^{+}\) which means as the resistance increases without bound, the power diminishes to zero.