4.2E: Exercises
- Page ID
- 120152
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Exercises
In Exercises 1 - 16, use the six-step procedure to graph the rational function. Be sure to draw any asymptotes as dashed lines.
- \(f(x) = \dfrac{4}{x + 2}\)
- \(f(x) = \dfrac{5x}{6 - 2x}\)
- \(f(x) = \dfrac{1}{x^{2}}\)
- \(f(x) = \dfrac{1}{x^{2} + x - 12}\)
- \(f(x) = \dfrac{2x - 1}{-2x^{2} - 5x + 3}\)
- \(f(x) = \dfrac{x}{x^{2} + x - 12}\)
- \(f(x) = \dfrac{4x}{x^2+4}\)
- \(f(x) = \dfrac{4x}{x^2-4}\)
- \(f(x) = \dfrac{x^2-x-12}{x^2+x-6}\)
- \(f(x) = \dfrac{3x^2-5x-2}{x^2-9}\)
- \(f(x) = \dfrac{x^2-x-6}{x+1}\)
- \(f(x) = \dfrac{x^2-x}{3-x}\)
- \(f(x) = \dfrac{x^3+2x^2+x}{x^2-x-2}\)
- \(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}\)
- \(f(x) = \dfrac{x^3-2x^2+3x}{2x^2+2}\)
- \(f(x) = \dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x}\)
In Exercises 17 - 20, graph the rational function by applying transformations to the graph of \(y = \dfrac{1}{x}\).
- \(f(x) = \dfrac{1}{x - 2}\)
- \(g(x) = 1 - \dfrac{3}{x}\)
- \(h(x) = \dfrac{-2x + 1}{x}\) (Hint: Divide)
- \(j(x) = \dfrac{3x - 7}{x - 2}\) (Hint: Divide)
- Discuss with your classmates how you would graph \(f(x) = \dfrac{ax + b}{cx + d}\). What restrictions must be placed on \(a, b, c\) and \(d\) so that the graph is indeed a transformation of \(y = \dfrac{1}{x}\)?
- In Example 3.1.1 in Section 3.1 we showed that \(p(x) = \frac{4x+x^3}{x}\) is not a polynomial even though its formula reduced to \(4 + x^{2}\) for \(x \neq 0\). However, it is a rational function similar to those studied in the section. With the help of your classmates, graph \(p(x)\).
- Let \(g(x) = \displaystyle \frac{x^{4} - 8x^{3} + 24x^{2} - 72x + 135}{x^{3} - 9x^{2} + 15x - 7}.\;\) With the help of your classmates, find the \(x\)- and \(y\)- intercepts of the graph of \(g\). Find the intervals on which the function is increasing, the intervals on which it is decreasing and the local extrema. Find all of the asymptotes of the graph of \(g\) and any holes in the graph, if they exist. Be sure to show all of your work including any polynomial or synthetic division. Sketch the graph of \(g\), using more than one picture if necessary to show all of the important features of the graph.
Example 4.2.4 showed us that the six-step procedure cannot tell us everything of importance about the graph of a rational function. Without Calculus, we need to use our graphing calculators to reveal the hidden mysteries of rational function behavior. Working with your classmates, use a graphing calculator to examine the graphs of the rational functions given in Exercises 24 - 27. Compare and contrast their features. Which features can the six-step process reveal and which features cannot be detected by it?
- \(f(x) = \dfrac{1}{x^{2} + 1}\)
- \(f(x) = \dfrac{x}{x^{2} + 1}\)
- \(f(x) = \dfrac{x^{2}}{x^{2} + 1}\)
- \(f(x) = \dfrac{x^{3}}{x^{2} + 1}\)
Answers
-
\(f(x) = \dfrac{4}{x + 2}\)
Domain: \((-\infty, -2) \cup (-2, \infty)\)
No \(x\)-intercepts
\(y\)-intercept: \((0, 2)\)
Vertical asymptote: \(x = -2\)
As \(x \rightarrow -2^{-}, \; f(x) \rightarrow -\infty\)
As \(x \rightarrow -2^{+}, \; f(x) \rightarrow \infty\)
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\)
As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)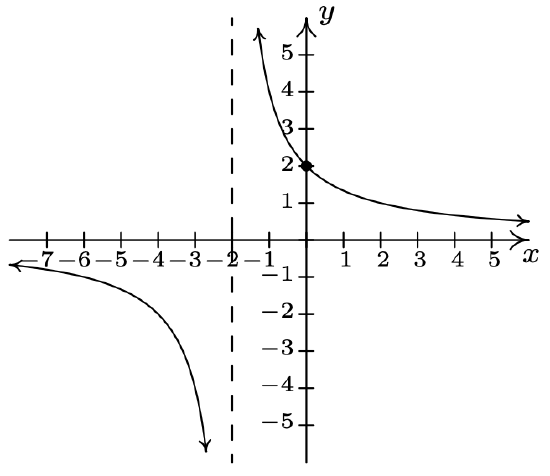
-
\(f(x) = \dfrac{5x}{6 - 2x}\)
Domain: \((-\infty, 3) \cup (3, \infty)\)
\(x\)-intercept: \((0, 0)\)
\(y\)-intercept: \((0, 0)\)
Vertical asymptote: \(x = 3\)
As \(x \rightarrow 3^{-}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty\)
Horizontal asymptote: \(y = -\frac{5}{2}\)
As \(x \rightarrow -\infty, \; f(x) \rightarrow -\frac{5}{2}^{+}\)
As \(x \rightarrow \infty, \; f(x) \rightarrow -\frac{5}{2}^{-}\)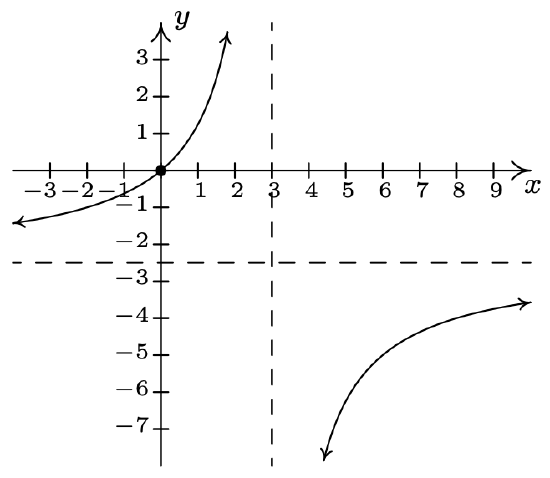
-
\(f(x) = \dfrac{1}{x^{2}}\)
Domain: \((-\infty, 0) \cup (0, \infty)\)
No \(x\)-intercepts
No \(y\)-intercepts
Vertical asymptote: \(x = 0\)
As \(x \rightarrow 0^{-}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow 0^{+}, \; f(x) \rightarrow \infty\)
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\)
As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)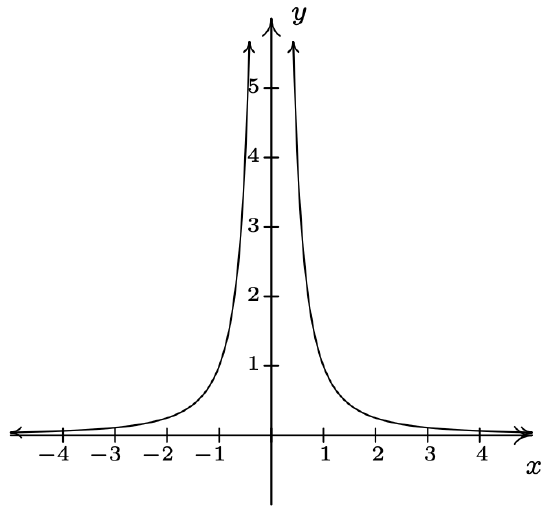
-
\(f(x) = \dfrac{1}{x^{2} + x - 12} = \dfrac{1}{(x - 3)(x + 4)}\)
Domain: \((-\infty, -4) \cup (-4, 3) \cup (3, \infty)\)
No \(x\)-intercepts
\(y\)-intercept: \((0, -\frac{1}{12})\)
Vertical asymptotes: \(x = -4\) and \(x = 3\)
As \(x \rightarrow -4^{-}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow -4^{+}, \; f(x) \rightarrow -\infty\)
As \(x \rightarrow 3^{-}, \; f(x) \rightarrow -\infty\)
As \(x \rightarrow 3^{+}, \; f(x) \rightarrow \infty\)
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\)
As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)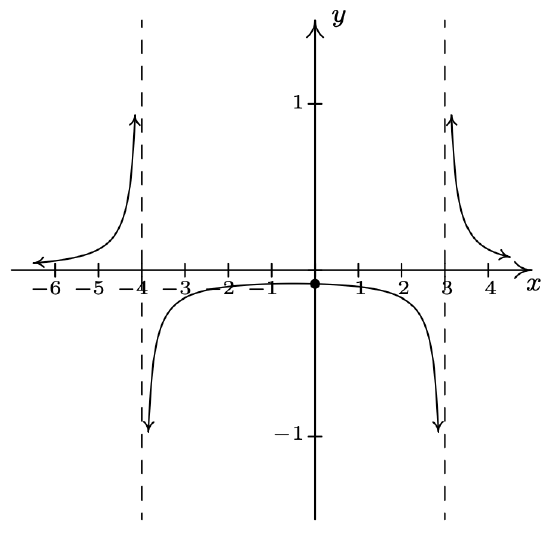
-
\(f(x) = \dfrac{2x - 1}{-2x^{2} - 5x + 3} = -\dfrac{2x - 1}{(2x - 1)(x + 3)}\)
Domain: \((-\infty, -3) \cup (-3, \frac{1}{2}) \cup (\frac{1}{2}, \infty)\)
No \(x\)-intercepts
\(y\)-intercept: \((0, -\frac{1}{3})\)
\(f(x) = \dfrac{-1}{x + 3}, \; x \neq \frac{1}{2}\)
Hole in the graph at \((\frac{1}{2}, -\frac{2}{7})\)
Vertical asymptote: \(x = -3\)
As \(x \rightarrow -3^{-}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow -3^{+}, \; f(x) \rightarrow -\infty\)
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{+}\)
As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{-}\)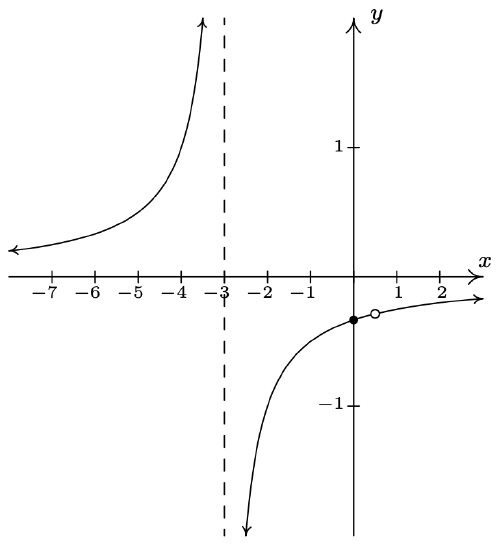
-
\(f(x) = \dfrac{x}{x^{2} + x - 12} = \dfrac{x}{(x - 3)(x + 4)}\)
Domain: \((-\infty, -4) \cup (-4, 3) \cup (3, \infty)\)
\(x\)-intercept: \((0, 0)\)
\(y\)-intercept: \((0, 0)\)
Vertical asymptotes: \(x = -4\) and \(x = 3\)
As \(x \rightarrow -4^{-}, \; f(x) \rightarrow -\infty\)
As \(x \rightarrow -4^{+}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow 3^{-}, \; f(x) \rightarrow -\infty\)
As \(x \rightarrow 3^{+}, \; f(x) \rightarrow \infty\)
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\)
As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)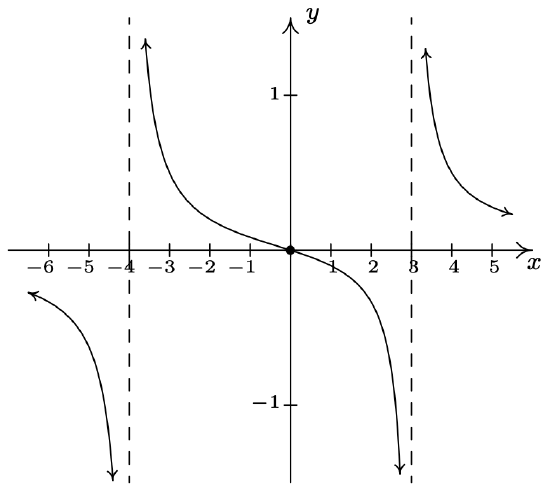
-
\(f(x) = \dfrac{4x}{x^{2} + 4}\)
Domain: \((-\infty, \infty)\)
\(x\)-intercept: \((0,0)\)
\(y\)-intercept: \((0,0)\)
No vertical asymptotes
No holes in the graph
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)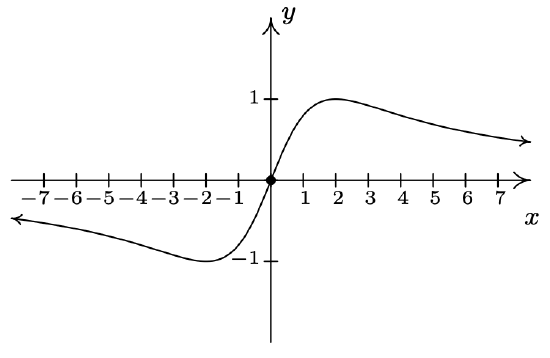
-
\(f(x) = \dfrac{4x}{x^{2} -4} = \dfrac{4x}{(x + 2)(x - 2)}\)
Domain: \((-\infty, -2) \cup (-2, 2) \cup (2, \infty)\)
\(x\)-intercept: \((0,0)\)
\(y\)-intercept: \((0,0)\)
Vertical asymptotes: \(x = -2, x = 2\)
As \(x \rightarrow -2^{-}, f(x) \rightarrow -\infty\)
As \(x \rightarrow -2^{+}, f(x) \rightarrow \infty\)
As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\)
As \(x \rightarrow 2^{+}, f(x) \rightarrow \infty\)
No holes in the graph
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, f(x) \rightarrow 0^{-}\)
As \(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)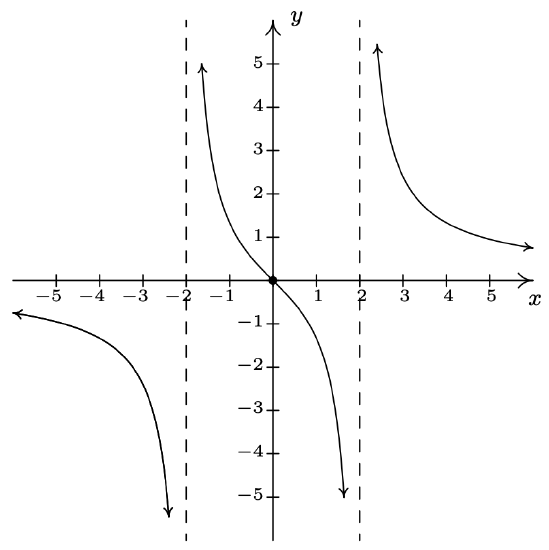
-
\(f(x) = \dfrac{x^2-x-12}{x^{2} +x - 6} = \dfrac{x-4}{x - 2} \, x \neq -3\)
Domain: \((-\infty, -3) \cup (-3, 2) \cup (2, \infty)\)
\(x\)-intercept: \((4,0)\)
\(y\)-intercept: \((0,2)\)
Vertical asymptote: \(x = 2\)
As \(x \rightarrow 2^{-}, f(x) \rightarrow \infty\)
As \(x \rightarrow 2^{+}, f(x) \rightarrow -\infty\)
Hole at \(\left(-3, \frac{7}{5} \right)\)
Horizontal asymptote: \(y = 1\)
As \(x \rightarrow -\infty, f(x) \rightarrow 1^{+}\)
As \(x \rightarrow \infty, f(x) \rightarrow 1^{-}\)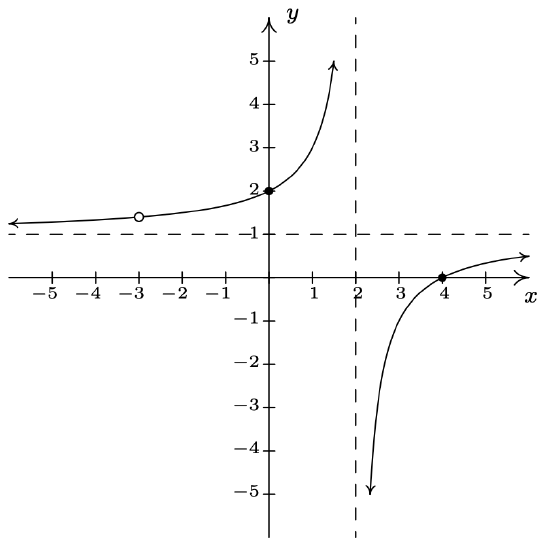
-
\(f(x) = \dfrac{3x^2-5x-2}{x^{2} -9} = \dfrac{(3x+1)(x-2)}{(x + 3)(x - 3)}\)
Domain: \((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\)
\(x\)-intercepts: \(\left(-\frac{1}{3}, 0 \right)\), \((2,0)\)
\(y\)-intercept: \(\left(0, \frac{2}{9} \right)\)
Vertical asymptotes: \(x = -3, x = 3\)
As \(x \rightarrow -3^{-}, f(x) \rightarrow \infty\)
As \(x \rightarrow -3^{+}, f(x) \rightarrow -\infty\)
As \(x \rightarrow 3^{-}, f(x) \rightarrow -\infty\)
As \(x \rightarrow 3^{+}, f(x) \rightarrow \infty\)
No holes in the graph
Horizontal asymptote: \(y = 3\)
As \(x \rightarrow -\infty, f(x) \rightarrow 3^{+}\)
As \(x \rightarrow \infty, f(x) \rightarrow 3^{-}\)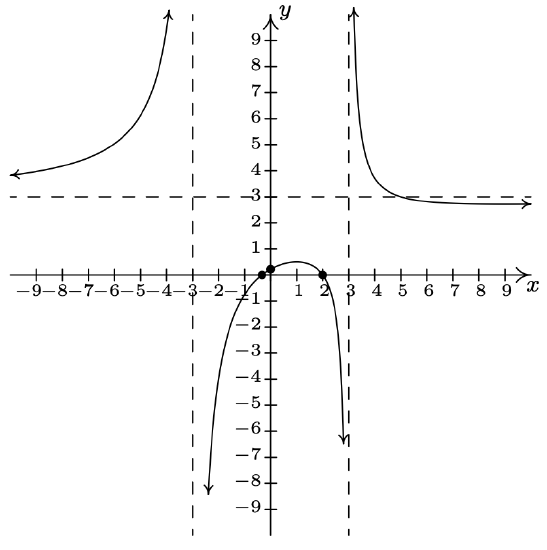
-
\(f(x) = \dfrac{x^2-x-6}{x+1} = \dfrac{(x-3)(x+2)}{x+1}\)
Domain: \((-\infty, -1) \cup (-1, \infty)\)
\(x\)-intercepts: \((-2,0)\), \((3,0)\)
\(y\)-intercept: \((0,-6)\)
Vertical asymptote: \(x = -1\)
As \(x \rightarrow -1^{-}, f(x) \rightarrow \infty\)
As \(x \rightarrow -1^{+}, f(x) \rightarrow -\infty\)
Slant asymptote: \(y = x-2\)
As \(x \rightarrow -\infty\), the graph is above \(y=x-2\)
As \(x \rightarrow \infty\), the graph is below \(y=x-2\)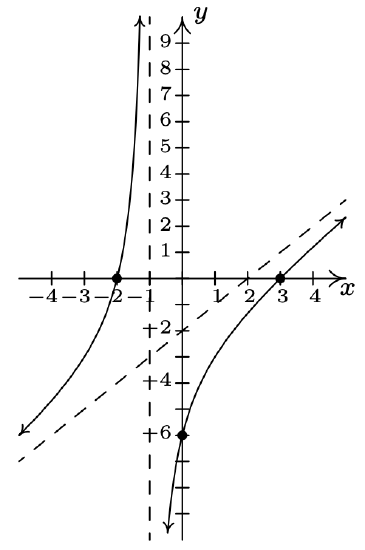
-
\(f(x) = \dfrac{x^2-x}{3-x} = \dfrac{x(x-1)}{3-x}\)
Domain: \((-\infty, 3) \cup (3, \infty)\)
\(x\)-intercepts: \((0,0)\), \((1,0)\)
\(y\)-intercept: \((0,0)\)
Vertical asymptote: \(x = 3\)
As \(x \rightarrow 3^{-}, f(x) \rightarrow \infty\)
As \(x \rightarrow 3^{+}, f(x) \rightarrow -\infty\)
Slant asymptote: \(y = -x-2\)
As \(x \rightarrow -\infty\), the graph is above \(y=-x-2\)
As \(x \rightarrow \infty\), the graph is below \(y=-x-2\)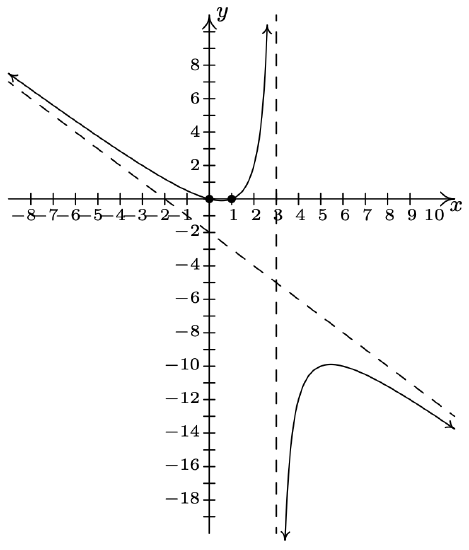
-
\(f(x) = \dfrac{x^3+2x^2+x}{x^{2} -x-2} = \dfrac{x(x+1)}{x - 2} \, x \neq -1\)
Domain: \((-\infty, -1) \cup (-1, 2) \cup (2, \infty)\)
\(x\)-intercept: \((0,0)\)
\(y\)-intercept: \((0,0)\)
Vertical asymptote: \(x = 2\)
As \(x \rightarrow 2^{-}, f(x) \rightarrow -\infty\)
As \(x \rightarrow 2^{+}, f(x) \rightarrow \infty\)
Hole at \((-1,0)\)
Slant asymptote: \(y = x+3\)
As \(x \rightarrow -\infty\), the graph is below \(y=x+3\)
As \(x \rightarrow \infty\), the graph is above \(y=x+3\)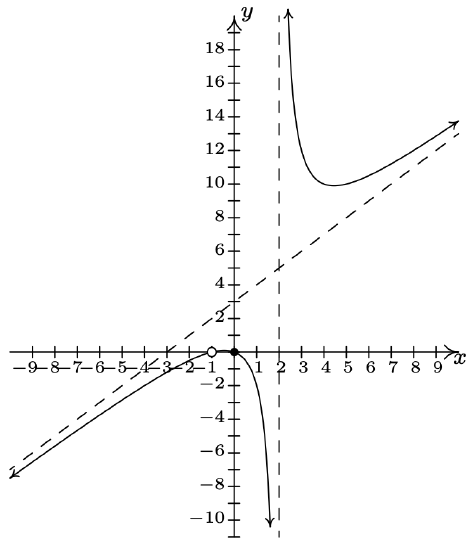
-
\(f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}\)
Domain: \((-\infty, -3) \cup (-3, 3) \cup (3, \infty)\)
\(x\)-intercepts: \((-2, 0), (0, 0), (2, 0)\)
\(y\)-intercept: \((0, 0)\)
Vertical asymptotes: \(x = -3, x = 3\)
As \(x \rightarrow -3^{-}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow -3^{+}, \; f(x) \rightarrow -\infty\)
As \(x \rightarrow 3^{-}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow 3^{+}, \; f(x) \rightarrow -\infty\)
Slant asymptote: \(y = -x\)
As \(x \rightarrow -\infty\), the graph is above \(y=-x\)
As \(x \rightarrow \infty\), the graph is below \(y=-x\)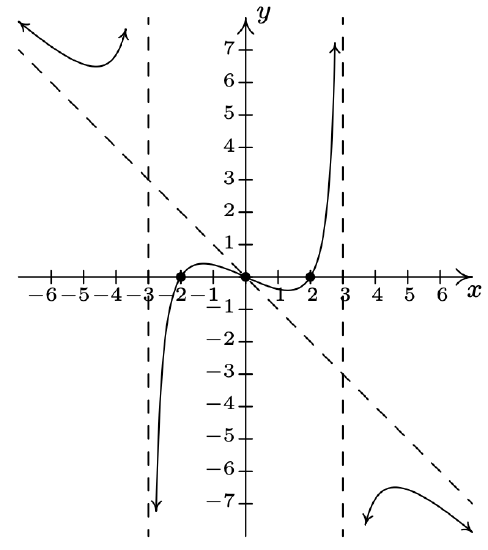
-
\(f(x) = \dfrac{x^3-2x^2+3x}{2x^2+2}\)
Domain: \((-\infty,\infty)\)
\(x\)-intercept: \((0,0)\)
\(y\)-intercept: \((0,0)\)
Slant asymptote: \(y = \frac{1}{2}x-1\)
As \(x \rightarrow -\infty\), the graph is below \(y = \frac{1}{2}x-1\)
As \(x \rightarrow \infty\), the graph is above \(y = \frac{1}{2}x-1\)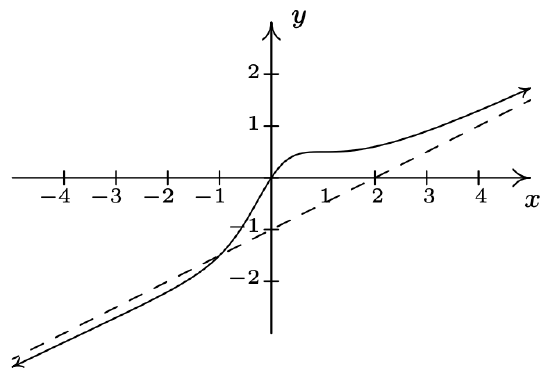
-
\(f(x) = \dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x}\)
Domain: \((-\infty, -2) \cup (-2, 0) \cup (0, 1) \cup (1, \infty)\)
\(f(x) = \dfrac{x - 1}{x(x + 2)}, \; x \neq 1\)
No \(x\)-intercepts
No \(y\)-intercepts
Vertical asymptotes: \(x = -2\) and \(x = 0\)
As \(x \rightarrow -2^{-}, \; f(x) \rightarrow -\infty\)
As \(x \rightarrow -2^{+}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow 0^{-}, \; f(x) \rightarrow \infty\)
As \(x \rightarrow 0^{+}, \; f(x) \rightarrow -\infty\)
Hole in the graph at \((1, 0)\)
Horizontal asymptote: \(y = 0\)
As \(x \rightarrow -\infty, \; f(x) \rightarrow 0^{-}\)
As \(x \rightarrow \infty, \; f(x) \rightarrow 0^{+}\)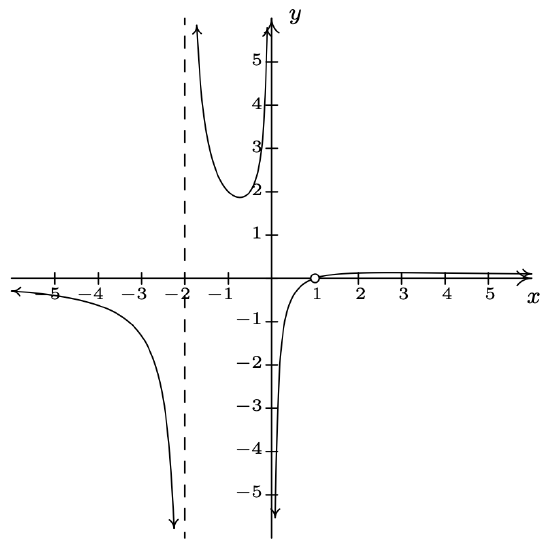
-
\(f(x) = \dfrac{1}{x - 2}\)
Shift the graph of \(y = \dfrac{1}{x}\)
to the right 2 units.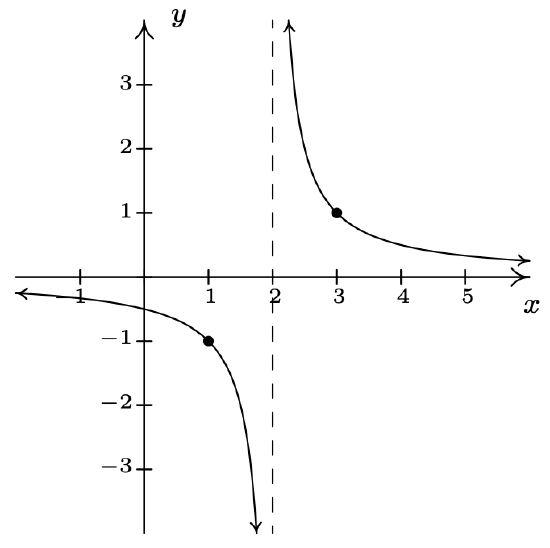
-
\(g(x) = 1 - \dfrac{3}{x}\)
Vertically stretch the graph of \(y = \dfrac{1}{x}\)
by a factor of 3.
Reflect the graph of \(y = \dfrac{3}{x}\)
about the \(x\)-axis.
Shift the graph of \(y = -\dfrac{3}{x}\)
up 1 unit.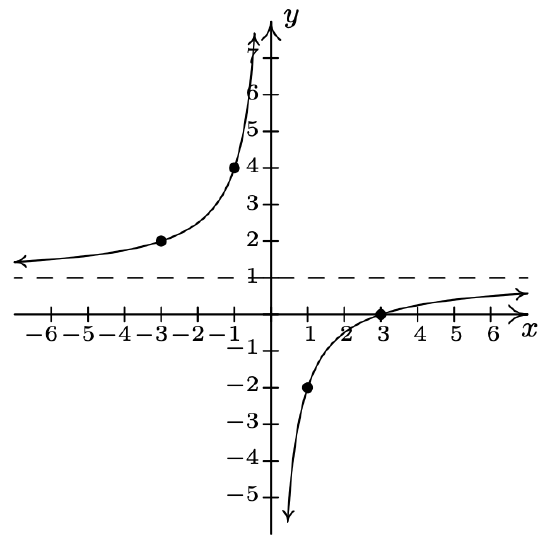
-
\(h(x) = \dfrac{-2x + 1}{x} = -2 + \dfrac{1}{x}\)
Shift the graph of \(y = \dfrac{1}{x}\)
down 2 units.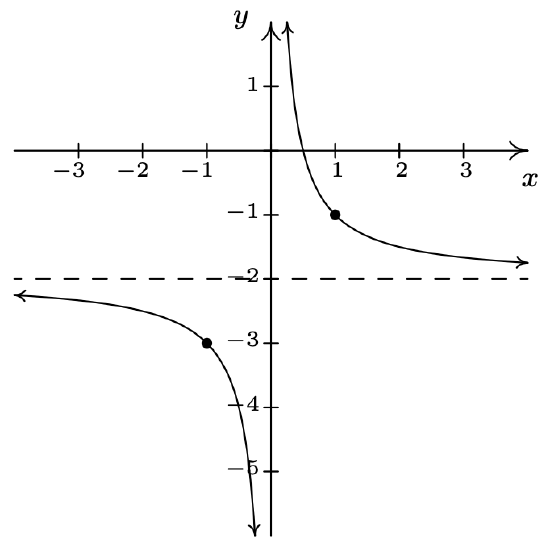
-
\(j(x) = \dfrac{3x - 7}{x - 2} = 3 - \dfrac{1}{x - 2}\)
Shift the graph of \(y = \dfrac{1}{x}\)
to the right 2 units.
Reflect the graph of \(y = \dfrac{1}{x - 2}\)
about the \(x\)-axis.
Shift the graph of \(y = -\dfrac{1}{x - 2}\)
up 3 units.