6.2: Sum and Difference Identities
- Page ID
- 145936
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use the Sum and Difference Identities to find the exact value of a trigonometric function.
- Prove an equation is an identity using the Sum and Difference Identities.
- Simplify an expression using the Sum and Difference Identities.
- Use the Sum and Difference Identities to graph an equation.
We have come a long way in Trigonometry. We have defined the trigonometric functions (in terms of angles, ratios of sides of right triangles, and real numbers), proved trigonometric identities with them, used them to solve applications, graphed them, and evaluated them by hand at the special angles. If we needed to evaluate a trigonometric function at a non-special angle, however, we must use technology. But, is this always the case?
For example, if we know the sine of \(27^{\circ}\), can we find the sine of \(2\left(27^{\circ}\right)=54^{\circ}\) without using a calculator? Or, if we know \(\cos \left(\alpha\right)\) and \(\cos \left(\beta\right)\), can we calculate \(\cos \left(\alpha+\beta\right)\)?
The Sum and Difference Identities for the Cosine
All the identities that relate the trigonometric ratios of different angles are derived from the Sum and Difference Identities (which really should be named the "Sum and Difference of Angles Identities," but that's too long to write). Let’s see why we need these formulas.
Is it true that\[\cos \left(\alpha+\beta\right) = \cos \left(\alpha\right)+\cos \left(\beta\right)?\nonumber \]We can test this hypothesis by evaluating both expressions for some specific values of \(\alpha\) and \(\beta\), say \(\alpha=45^{\circ}\) and \(\beta=30^{\circ}\), as shown below.

Taking a unit circle approach, you should be able to see that \(\cos \left(75^{\circ}\right)\) (which is the \( x \)-value of the point on the terminal side of \( 75^{ \circ } \)) is in fact smaller than either \(\cos \left(45^{\circ}\right)\) or \(\cos \left(30^{\circ}\right)\). Therefore, it cannot be true that \(\cos \left(75^{\circ}\right)\) is equal to \(\cos \left(45^{\circ}\right)+\cos \left(30^{\circ}\right)\).
Verify that \(\cos \left(45^{\circ}+30^{\circ}\right)\) is not equal to \(\cos \left(45^{\circ}\right)+\cos \left(30^{\circ}\right)\).
- Solution
-
We know that \( \cos\left( 45^{ \circ } \right) = \frac{1}{\sqrt{2}} \approx 0.7071 \) and \( \cos\left( 30^{ \circ } \right) = \frac{\sqrt{3}}{2} \approx 0.8660 \). Thus, \( \cos\left( 45^{ \circ } \right) + \cos\left( 30^{ \circ } \right) \approx 1.5731 \). For \( \cos\left( 45^{ \circ } + 30^{ \circ } \right) = \cos\left( 75^{ \circ } \right) \), we use a calculator to get the approximation \( 0.2588 \). Therefore, the two expressions are not equal.
Show that \(\sin \left(60^{\circ}+30^{\circ}\right)\) is not equal to \(\sin \left(60^{\circ}\right)+\sin \left(30^{\circ}\right)\).
- Answer
-
\(\quad \sin \left(60^{\circ}+30^{\circ}\right)=1\), but \(\sin \left(60^{\circ}\right)+\sin \left(30^{\circ}\right)=\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\)
Because the values of the expressions in the Example \( \PageIndex{ 1 } \) and Exercise \( \PageIndex{ 1 } \) are different, it is not true that \(\cos (\alpha+\beta)\) is equal to \(\cos \left(\alpha\right)+\cos \left(\beta\right)\) for all angles \(\alpha\) and \(\beta\), or that \(\sin (\alpha+\beta)\) is equal to \(\sin \left(\alpha\right)+\sin \left(\beta\right)\).
This is a general property of almost all functions. That is, if \( f \) is a function, it is generally the case that\[ f\left( a \pm b \right) \neq f\left( a \right) \pm f\left( b \right). \nonumber \]
It turns out that there is a relationship between the trigonometric ratios for \(\alpha+\beta\) and the trigonometric ratios of \(\alpha\) and \(\beta\). To derive the formulas (yes, plural), we will start by considering a difference of two angles.
Let \( \alpha \) and \( \beta \) be angles in standard position and let \( \alpha_0 \) and \( \beta_0 \) be the angles coterminal to \( \alpha \) and \( \beta \), respectively, each of which measure between \(0\) and \(2\pi\) radians. Moreover, without loss of generality,1 let's assume that \( \alpha \) is such that \( \alpha_0 \gt \beta_0 \).2
Since \( \alpha_0 \) is coterminal with \( \alpha \), \( \alpha = \alpha_0 + 2\pi m \) for some \( m \in \mathbb{Z} \). Likewise, \( \beta = \beta_0 + 2\pi n \) for some \( n \in \mathbb{Z} \). Therefore,\[ \cos\left( \alpha - \beta \right) = \cos\left( \alpha_0 + 2\pi m - \left( \beta_0 + 2\pi n \right) \right) = \cos\left( \alpha_0 - \beta_0 + 2 \pi(m - n) \right). \nonumber \]Since \( m \) and \( n \) are both integers, \( m -n \) is also an integer. Moreover, cosine has a period of \( 2 \pi \) means that \( \cos\left( \alpha_0 - \beta_0 + 2 \pi(m - n) \right) = \cos\left( \alpha_0 - \beta_0 \right) \). Thus,\[ \cos\left( \alpha - \beta \right) = \cos\left( \alpha_0 - \beta_0 \right). \label{eq1} \]We now draw label the points \( P \) and \( Q \) on the unit circle which are on the terminal sides of \( \alpha_0 \) and \( \beta_0 \), respectively.

Notice that we also drew a second image where we rotated both points clockwise \( \beta_0 \) radians. Since the angles \(\angle POQ\) and \( \angle AOB\) are congruent, the distance between \(P\) and \(Q\) is equal to the distance between \(A\) and \(B\).3 The Distance Formula yields\[ \begin{array}{rrclcr}
& \sqrt{\left(\cos \left(\alpha_{0}\right)-\cos \left(\beta_{0}\right)\right)^{2}+\left(\sin \left(\alpha_{0}\right)-\sin \left(\beta_{0}\right)\right)^{2}} & = & \sqrt{\left(\cos \left(\alpha_{0}-\beta_{0}\right)-1\right)^{2}+\left(\sin \left(\alpha_{0}-\beta_{0}\right)-0\right)^{2}} & \quad & \\
& & & & & \\
\hline \implies & \left(\cos \left(\alpha_{0}\right)-\cos \left(\beta_{0}\right)\right)^{2}+\left(\sin \left(\alpha_{0}\right)-\sin \left(\beta_{0}\right)\right)^{2} & = & \left(\cos \left(\alpha_{0}-\beta_{0}\right)-1\right)^{2}+ \left(\sin \left(\alpha_{0}-\beta_{0}\right)-0\right)^{2} & \quad & \left( \text{squaring both sides} \right) \\
& & & & & \\
\hline \implies & \begin{array}{c}
\cos^2 \left(\alpha_{0}\right) - 2 \cos\left( \alpha_0 \right) \cos\left( \beta_0 \right)+ \cos^2 \left(\beta_{0}\right) \\
+\sin^2 \left(\alpha_{0}\right) - 2 \sin\left( \alpha_0 \right) \sin\left( \beta_0 \right)+\sin^2 \left(\beta_{0}\right) \\
\end{array} & = & \begin{array}{c}
\cos^2 \left(\alpha_{0}-\beta_{0}\right)-2 \cos\left( \alpha_0 - \beta_0 \right)+1 \\
+ \sin^2 \left(\alpha_{0}-\beta_{0}\right) \\
\end{array} & \quad & \left( \text{distribution} \right) \\
& & & & & \\
\hline \implies & \begin{array}{c}
\cos^2 \left(\alpha_{0}\right) +\sin^2 \left(\alpha_{0}\right) \\
- 2 \cos\left( \alpha_0 \right) \cos\left( \beta_0 \right) - 2 \sin\left( \alpha_0 \right) \sin\left( \beta_0 \right) \\
+ \cos^2 \left(\beta_{0}\right)+\sin^2 \left(\beta_{0}\right) \\
\end{array} & = & \begin{array}{c}
\cos^2 \left(\alpha_{0}-\beta_{0}\right) + \sin^2 \left(\alpha_{0}-\beta_{0}\right) \\
-2 \cos\left( \alpha_0 - \beta_0 \right) \\
+1\\
\end{array} & \quad & \left( \text{Commutative Property of Addition} \right) \\
& & & & & \\
\hline \implies & \begin{array}{c}
1 \\
- 2 \cos\left( \alpha_0 \right) \cos\left( \beta_0 \right) - 2 \sin\left( \alpha_0 \right) \sin\left( \beta_0 \right) \\
+ 1 \\
\end{array} & = & \begin{array}{c}
1 \\
-2 \cos\left( \alpha_0 - \beta_0 \right) \\
+1\\
\end{array} & \quad & \left( \text{Pythagorean Identity} \right) \\
& & & & & \\
\hline \implies & 2 - 2 \cos\left( \alpha_0 \right) \cos\left( \beta_0 \right) - 2 \sin\left( \alpha_0 \right) \sin\left( \beta_0 \right) & = & 2 - 2 \cos\left( \alpha_0 - \beta_0 \right) & \quad & \\
& & & & & \\
\hline \implies & - 2 \cos\left( \alpha_0 \right) \cos\left( \beta_0 \right) - 2 \sin\left( \alpha_0 \right) \sin\left( \beta_0 \right) & = & - 2 \cos\left( \alpha_0 - \beta_0 \right) & \quad & \left( \text{subtract }2\text{ from both sides} \right)\\
& & & & & \\
\hline \implies & \cos\left( \alpha_0 \right) \cos\left( \beta_0 \right) + \sin\left( \alpha_0 \right) \sin\left( \beta_0 \right) & = & \cos\left( \alpha_0 - \beta_0 \right) & \quad & \left( \text{divide both sides by }-2 \right)\\
\end{array} \nonumber \]Combining this result with Equation \ref{eq1}, we have the identity\[ \cos\left( \alpha - \beta \right) = \cos\left( \alpha \right) \cos\left( \beta \right) + \sin\left( \alpha \right) \sin\left( \beta \right). \label{cdiff}\]To get the sum identity for cosine, we use the our result from Formula \ref{cdiff} along with the Symmetry Identities.\[\cos (\alpha+\beta)=\cos (\alpha-(-\beta))=\cos (\alpha) \cos (-\beta)+\sin (\alpha) \sin (-\beta)=\cos (\alpha) \cos (\beta)-\sin (\alpha) \sin (\beta)\nonumber\]Hence,\[ \cos\left( \alpha + \beta \right) = \cos\left( \alpha \right) \cos\left( \beta \right) - \sin\left( \alpha \right) \sin\left( \beta \right). \label{csum} \]Most people combine Formulas \ref{cdiff} and \ref{csum} into a single statement, which is how we present it in the following theorem.
For any angles \( \alpha \) and \( \beta \),\[ \cos\left( \alpha \pm \beta \right) = \cos\left( \alpha \right) \cos\left( \beta \right) \mp \sin\left( \alpha \right) \sin\left( \beta \right). \nonumber \]
The \( \pm \) and \( \mp \) signs on the left and right side of this identity are always opposite.
The Sum and Difference Identities for the cosine are needed throughout the rest of Trigonometry, Calculus, and Differential Equations. While not as prevalent as the Pythagorean Theorem or the Quadratic Formula, the need to commit them to memory and their importance cannot be overstated.
Notice that to find the cosine of \(\alpha+\beta\) we must know (or be able to find) both trigonometric ratios for both and \(\alpha\) and \(\beta\).
The Sum and Difference Identities can be used to find exact values for trigonometric ratios of various angles.
Find an exact value for \(\cos \left(105^{\circ}\right)\).
- Solution
-
We can write \(105^{\circ}\) as the sum of two special angles: \(105^{\circ}=60^{\circ}+45^{\circ}\). Now apply the sum of angles identity for the cosine.\[\begin{array}{rcl}
\cos \left(60^{\circ}+45^{\circ}\right) & = & \cos \left(60^{\circ}\right) \cos \left(45^{\circ}\right)-\sin \left(60^{\circ}\right) \sin \left(45^{\circ}\right) \\
& = & \dfrac{1}{2} \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{3}}{2} \dfrac{\sqrt{2}}{2} \\
& = & \dfrac{\sqrt{2}-\sqrt{6}}{4}
\end{array} \nonumber \]Thus, \(\cos 105^{\circ}=\frac{\sqrt{2}-\sqrt{6}}{4}\). You can check that your calculator gives the same decimal approximation of about \(-0.2588\) for both \(\cos 105^{\circ}\) and \(\frac{\sqrt{2}-\sqrt{6}}{4}\).
Suppose that \(\sin \left(\theta\right)=\frac{-5}{13}\) and \(\cos \left(\theta\right)=\frac{12}{13}\). Find an exact value for \(\cos \left(\frac{\pi}{4}+\theta\right)\).
- Answer
-
\(\dfrac{17}{13 \sqrt{2}}=\dfrac{17 \sqrt{2}}{26}\)
Proving the Cofunction Identities
We have been using the Cofunction Identities for quite a while, but have yet to see a proof. This is usually unforgivable in Mathematics; however, I wanted you to have some experience with these identities and, at the time, we didn't have the "mathematical technology" (read as, the knowledge) to prove them - now, we do. Let's prove \( \cos\left( \frac{\pi}{2} - \theta \right) = \sin\left( \theta \right) \).\[ \begin{array}{rclcl}
\cos\left( \dfrac{\pi}{2} - \theta \right) & = & \cos\left( \dfrac{\pi}{2} \right) \cos\left( \theta \right) + \sin\left( \dfrac{\pi}{2} \right) \sin\left( \theta \right) & \quad & \left( \text{Difference Identity for the Cosine} \right) \\
& = & (0) \cos\left( \theta \right) + (1) \sin\left( \theta \right) & \quad & \left( \text{evaluating trig functions} \right) \\
& = & \sin\left( \theta \right) & & \\
\end{array} \nonumber \]The remaining Cofunction Identities are left for you to prove as exercises.
The Sum and Difference Identities for the Sine
To prove the Sum and Difference Identities for the sine, we make use of the fact the Cofunction Identity we just proved.\[ \begin{array}{rclcl}
\sin(\alpha + \beta) & = & \cos{\left( \frac{\pi}{2} - (\alpha + \beta) \right)} & \quad & \left( \text{Cofunction Identities} \right)\\
& = & \cos{\left( \left(\frac{\pi}{2} - \alpha \right) - \beta \right)} & & \left( \text{Associative Property of Addition} \right) \\
& = & \cos{\left(\frac{\pi}{2} - \alpha \right)} \cos\left(\beta\right) + \sin{\left(\frac{\pi}{2} - \alpha \right)} \sin\left(\beta\right) & & \left( \text{Difference Identity for Cosine} \right) \\
& = & \sin\left(\alpha\right) \cos\left(\beta\right) + \sin{\left(\frac{\pi}{2} - \alpha \right)} \sin\left(\beta\right) & & \left( \text{Cofunction Identities} \right) \\
& = & \sin\left(\alpha\right) \cos\left(\beta\right) + \cos{\left( \alpha \right)} \sin\left(\beta\right) & & \left( \text{Cofunction Identities} \right) \\
\end{array} \nonumber \]Thus, we get the identity.\[ \sin\left( \alpha + \beta \right) = \sin\left( \alpha \right) \cos\left( \beta \right) + \cos\left( \alpha \right) \sin\left( \beta \right). \nonumber \]A similiar proof shows that\[ \sin\left( \alpha - \beta \right) = \sin\left( \alpha \right) \cos\left( \beta \right) - \cos\left( \alpha \right) \sin\left( \beta \right). \nonumber \]The following theorem has these two formulas written more succinctly.
For any angles \( \alpha \) and \( \beta \),\[ \sin\left( \alpha \pm \beta \right) = \sin\left( \alpha \right)\cos\left( \beta \right) \pm \cos\left( \alpha \right) \sin\left( \beta \right). \nonumber \]
Notice that the sine function "keeps its sign." That is, if we are given \( \alpha + \beta \), the result will be a sum of functions. If given \( \alpha - \beta \), we will have a difference of functions.
The Sum and Difference Identities for the sine are needed throughout the rest of Trigonometry, Calculus, and Differential Equations. While not as prevalent as the Pythagorean Theorem or the Quadratic Formula, the need to commit them to memory and their importance cannot be overstated.
Suppose that \(\sin \left(\theta\right)=0.6\) and \(\cos \left(\theta\right)=-0.8\). Find an exact value for \(\sin \left(\theta+\frac{2 \pi}{3}\right)\).
- Solution
-
Recall that \(\sin \left(\frac{2 \pi}{3}\right)=\frac{\sqrt{3}}{2}\) and \(\cos \left(\frac{2 \pi}{3}\right)=\frac{-1}{2}\). Substituting these values into the sum formula for sine, we find\[ \begin{array}{rcl}
\sin \left(\theta+\dfrac{2 \pi}{3}\right) & = & \sin \left(\theta\right) \cos \left(\dfrac{2 \pi}{3}\right)+ \cos\left( \theta\right) \sin\left( \dfrac{2 \pi}{3} \right) \\
& = & 0.6\left(\dfrac{-1}{2}\right)+(-0.8)\left(\dfrac{\sqrt{3}}{2}\right) \\
& = & \dfrac{3}{5} \cdot \dfrac{-1}{2}+ \dfrac{-4}{5} \cdot \dfrac{\sqrt{3}}{2} \\
& = & \dfrac{-3-4 \sqrt{3}}{10}
\end{array}\nonumber \]
Find the exact value of \(\sin\left(\frac{19 \pi}{12}\right)\).
- Solution
-
We need to write the angle \(\frac{19 \pi}{12}\) as a sum or difference of common angles. The denominator of \(12\) suggests a combination of angles with denominators \(3\) and \(4\). One such combination is \( \frac{19 \pi}{12} = \frac{16 \pi}{12} + \frac{3 \pi}{12} = \frac{4 \pi}{3} + \frac{\pi}{4}\). We get\[\begin{array}{rcl}
\sin\left(\dfrac{19 \pi}{12}\right) & = & \sin\left(\dfrac{4 \pi}{3} + \dfrac{\pi}{4} \right) \\
& = & \sin\left(\dfrac{4 \pi}{3} \right)\cos\left(\dfrac{\pi}{4} \right) + \cos\left(\dfrac{4 \pi}{3} \right)\sin\left(\dfrac{\pi}{4} \right) \\
& = & \left( -\dfrac{\sqrt{3}}{2} \right)\left( \dfrac{\sqrt{2}}{2} \right) + \left( -\dfrac{1}{2} \right) \left( \dfrac{\sqrt{2}}{2} \right) \\
& = & \dfrac{-\sqrt{6}- \sqrt{2}}{4} \\
\end{array}\nonumber\]
Evaluate \(\sin \left(\frac{7\pi}{12}\right)\) exactly.
- Answer
-
\( \dfrac{\sqrt{3}+1}{2 \sqrt{2}}\)
If \(\alpha\) is a Quadrant II angle with \(\sin(\alpha) = \frac{5}{13}\), and \(\beta\) is a Quadrant III angle with \(\tan(\beta) = 2\), find \(\sin(\alpha - \beta)\).
- Solution
- This is one of my favorite styles of problems. There are two main ways to find the solution - using identities or using right triangle trigonometry. I will cover both methods here, but I must confess - I highly prefer the right triangle approach.
Using Identities
In order to find \(\sin(\alpha - \beta) = \sin\left( \alpha \right) \cos\left( \beta \right) - \cos\left( \alpha \right)\sin\left( \beta \right)\), we need to find \(\cos(\alpha)\) and both \(\cos(\beta)\) and \(\sin(\beta)\). To find \(\cos(\alpha)\), we use the Pythagorean Identity \(\cos^2(\alpha) + \sin^2(\alpha) = 1\). Since \(\sin(\alpha) = \frac{5}{13}\), we have \(\cos^{2}(\alpha) + \left(\frac{5}{13}\right)^2 = 1\), or \(\cos(\alpha) = \pm \frac{12}{13}\). Since \(\alpha\) is a Quadrant II angle, \(\cos(\alpha) = -\frac{12}{13}\). We now set about finding \(\cos(\beta)\) and \(\sin(\beta)\). We have several ways to proceed, but the Pythagorean Identity \(1 + \tan^{2}(\beta) = \sec^{2}(\beta)\) is a quick way to get \(\sec(\beta)\), and hence, \(\cos(\beta)\). With \(\tan(\beta) = 2\), we get \(1 + 2^2 = \sec^{2}(\beta)\) so that \(\sec(\beta) = \pm \sqrt{5}\). Since \(\beta\) is a Quadrant III angle, we choose \(\sec(\beta) = -\sqrt{5}\) so \(\cos(\beta) = \frac{1}{\sec(\beta)} = \frac{1}{-\sqrt{5}} = -\frac{\sqrt{5}}{5}\). We now need to determine \(\sin(\beta)\). We could use The Pythagorean Identity \(\cos^{2}(\beta) + \sin^{2}(\beta) = 1\), but we opt instead to use a quotient identity. From \(\tan(\beta) = \frac{\sin(\beta)}{\cos(\beta)}\), we have \(\sin(\beta) = \tan(\beta) \cos(\beta)\) so we get \(\sin(\beta) = (2) \left( -\frac{\sqrt{5}}{5}\right) = - \frac{2 \sqrt{5}}{5}\). We now have all the pieces needed to find \(\sin(\alpha - \beta)\):\[\begin{array}{rcl}
\sin(\alpha - \beta) & = & \sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta) \\
& = & \left( \dfrac{5}{13} \right)\left( -\dfrac{\sqrt{5}}{5} \right) - \left( -\dfrac{12}{13} \right)\left( - \dfrac{2 \sqrt{5}}{5} \right) \\
& = & -\dfrac{29\sqrt{5}}{65} \\
\end{array}\nonumber\]
Using Right Triangle Trigonometry
For this method, we remind ourselves that Trigonometry is mostly about quadrants and reference angles. We draw \( \alpha \in \mathrm{QII} \) and \( \beta \in \mathrm{QIII} \) and their corresponding reference angles. Neither of these graphs are drawn to scale, nor do they need to be. Since \( \sin\left( \alpha \right) = \frac{5}{13} \), we wisely choose the terminal point so that its \( y \)-value is \( 5 \) and its distance to the origin is \( 13 \). Looking at the reference triangle, this should remind you that sine is opposite over hypotenuse. Likewise, since \( \tan\left( \beta \right) = 2 = \frac{2}{1} \), we choose the terminal point of \( \beta \) to have a \( y \)-value of \( -2 \) (remember, \( \beta \in \mathrm{QIII} \)) and an \( x \)-value of \( -1 \). Again, the tangent is opposite over adjacent, so the tangent of \( \hat{\beta} \) is \( \frac{-2}{-1} = 2 \). Finally, we use the Pythagorean Theorem to help fill in the missing sides (taking into account the quadrants). From these figures, we read off the information we need.\[ \sin\left( \alpha - \beta \right) = \sin\left( \alpha \right) \cos\left( \beta \right) - \cos\left( \alpha \right)\sin\left( \beta \right) = \dfrac{5}{13} \cdot \dfrac{-1}{\sqrt{5}} - \dfrac{-12}{13} \cdot \dfrac{-2}{\sqrt{5}}= \dfrac{-5 + (-24) }{13 \sqrt{5}} = -\dfrac{29}{13\sqrt{5}}. \nonumber \]
If \(\alpha\) is a Quadrant II angle with \(\sin(\alpha) = \frac{3}{5}\), and \(\beta\) is a Quadrant III angle with \(\cos(\beta) = -\frac{5}{13}\), find \(\cos(\alpha - \beta)\).
- Answer
-
\( -\frac{56}{65} \)
The Sum and Difference Identities for the Tangent
There are also sum and difference formulas for the tangent. The proof for the tangent versions involves using the Quotient Identities to rewrite the tangent in terms of the sine and cosine, which we leave for you in the homework area.
For any angles \( \alpha \) and \( \beta \) where the following formula is defined,\[ \tan\left( \alpha \pm \beta \right) = \dfrac{\tan\left( \alpha \right) \pm \tan\left( \beta \right)}{1 \mp \tan\left( \alpha \right) \tan\left( \beta \right)} \nonumber \]
There is a subtle restriction in the last theorem that the two before it didn't have. Since the tangent function does not have a domain consisting of all real numbers, the Sum and Difference Identities for the tangent have exceptions whenever \( \alpha \) or \( \beta \) are odd multiples of \( \frac{\pi}{2} \); however, this theorem is rarely used and, as such, this exception is not going to be encountered (at least, not at this level).
Find an exact value for \(\tan \left(75^{\circ}\right)\).
- Solution
-
We observe that \(75^{\circ}=45^{\circ}+30^{\circ}\), so \(\tan \left(75^{\circ}\right)=\tan \left(45^{\circ}+30^{\circ}\right)\). We can apply the sum formula for tangent.\[\begin{array}{rcl}
\tan \left(45^{\circ}+30^{\circ}\right) & = & \dfrac{\tan \left(45^{\circ}\right)+\tan \left(30^{\circ}\right)}{1-\tan \left(45^{\circ}\right) \tan \left(30^{\circ}\right)} \\
& = & \dfrac{1+\frac{1}{\sqrt{3}}}{1-1\left(\frac{1}{\sqrt{3}}\right)} \cdot \dfrac{\sqrt{3}}{\sqrt{3}} \\
& = & \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \\
\end{array} \nonumber \]
Evaluate \(\tan \left(\frac{\pi}{12}\right)\) exactly.
- Answer
-
\(\quad \dfrac{\sqrt{3}-1}{\sqrt{3}+1}\)
Revisiting Proofs of Identities
Every time we introduce a new set of major identities (like the Sum and Difference Identities), we get to practice proofs again. In some sense, proofs begin to get much easier once we learn identities like the Sum and Difference Identities. This is because one of the first things we should look for when trying to prove an identity is the existence of other identities within the claim. That is, we look for Pythagorean Identities, Symmetry Identities, and so on. Now we have a new set of identities to look for.
Prove the following identity.\[ \dfrac{\sin\left( \alpha - \beta \right)}{\cos\left( \alpha \right) \cos\left( \beta \right)} = \tan\left( \alpha \right) - \tan\left( \beta \right)\nonumber \]
- Solution
- The left side is the more complex side, so we start there. Also, we immediately spot our newly-discovered Sum and Difference Identities, so we know where to begin.\[ \begin{array}{rclcl}
\dfrac{\sin\left( \alpha - \beta \right)}{\cos\left( \alpha \right) \cos\left( \beta \right)} & = & \dfrac{\sin\left( \alpha \right) \cos\left( \beta \right) - \cos\left( \alpha \right)\sin\left( \beta \right) }{\cos\left( \alpha \right) \cos\left( \beta \right)} & \quad & \left( \text{Sum and Difference Identities} \right) \\
& = & \dfrac{\sin\left( \alpha \right) \cos\left( \beta \right)}{\cos\left( \alpha \right) \cos\left( \beta \right)} - \dfrac{\cos\left( \alpha \right)\sin\left( \beta \right)}{\cos\left( \alpha \right) \cos\left( \beta \right)} & & \left( \text{property of fractions} \right) \\
& = & \dfrac{\sin\left( \alpha \right) \cancel{\cos\left( \beta \right)}}{\cos\left( \alpha \right) \cancel{\cos\left( \beta \right)}} - \dfrac{\cancel{\cos\left( \alpha \right)}\sin\left( \beta \right)}{\cancel{\cos\left( \alpha \right)} \cos\left( \beta \right)} & & \left( \text{cancel like factors} \right) \\
& = & \dfrac{\sin\left( \alpha \right) }{\cos\left( \alpha \right) } - \dfrac{\sin\left( \beta \right) }{ \cos\left( \beta \right)} & & \\
& = & \tan\left( \alpha \right) - \tan\left( \beta \right) & & \left( \text{Ratio Identities} \right) \\
\end{array} \nonumber \]
Prove.\[ \sin\left( \alpha + \beta \right) + \sin\left( \alpha - \beta \right) = 2 \sin\left( \alpha \right) \cos\left( \beta \right) \nonumber \]
Revisiting Graphs of Trigonometric Functions
The Sum and Difference Identities allow us to expand the set of trigonometric functions we can graph. Up to this point, we have only been able to graph functions of the form\[ f(x) = A \, \mathrm{trig}\left( Bx + C \right) + D. \nonumber \]However, now we can graph certain combinations of trigonometric functions. Specifically, those having the form of the Sum and Difference Identities.
Graph the function.\[ f(x) = \frac{1}{2}\cos\left( 2x \right) \cos\left( 3x \right) - \frac{1}{2}\sin\left( 2x \right)\sin\left( 3x \right) \nonumber \]
- Solution
- Prior to this moment, there would have been no possibility for us to graph this function by hand; however, we now know, from the Sum and Difference Identities, that\[ f(x) = \dfrac{1}{2}\cos\left( 2x \right) \cos\left( 3x \right) - \dfrac{1}{2}\sin\left( 2x \right)\sin\left( 3x \right) = \dfrac{1}{2}\left[\cos\left( 2x \right) \cos\left( 3x \right) - \sin\left( 2x \right)\sin\left( 3x \right) \right] = \dfrac{1}{2} \cos\left( 2x + 3x \right) = \dfrac{1}{2} \cos\left( 5x \right).\nonumber \]The amplitude of this cosine function is \( \frac{1}{2} \), the period is \( \frac{2\pi}{5} \), the step size is \( \frac{\pi}{10} \), the phase shift is \( 0 \), and the vertical shift is \( 0 \). Putting this together, we get the following graph.
Footnotes
1 The phrase, "without loss of generality," is used a lot in Mathematics. It means that the assumption following the statement is chosen arbitrarily, narrowing the premise to a particular case, but does not affect the validity of the proof in general.
2 If this were not the case, we would just relabel our variables accordingly.
3 In the picture we've drawn, the triangles \( \triangle POQ \) and \( \triangle AOB \) are congruent, which is even better. However, \( \alpha_0 - \beta_0 \) could be \( 0 \) or it could be \( \pi \), neither of which makes a triangle. It could also be larger than \( \pi \), which makes a triangle, just not the one we've drawn. You should think about those three cases.
Skills Refresher
For Problems 1 - 6,
(a) Compute \(f(2), f(3)\), and \(f(2+3)\).
(b) Determine if it is true that \(f(a+b)=f(a)+f(b)\) whenever the function values are defined.
-
\(f(x)=3 x+2\)
-
\(f(x)=x^2\)
-
\(f(x)=\sqrt{x}\)
-
\(f(x)=\dfrac{1}{x}\)
-
\(f(x)=|x|\)
-
\(f(x)=2^x\)
- Answers
-
-
-
8, 11, 17
-
Not true
-
-
-
4, 9, 25
-
Not true
-
-
-
\(\sqrt{2}, \sqrt{3}, \sqrt{5}\)
-
Not true
-
-
-
\(\dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{5}\)
-
Not true
-
-
-
2, 3, 5
-
Not true
-
-
-
4, 8, 32
-
Not true
-
-
Homework
Concept Check
-
Explain why \(f(a+b)-f(a)+f(b)\) is not a valid application of the Distributive Law.
-
Nhat says that \(\sin \left(\theta+\frac{\pi}{6}\right)=\frac{1}{2}+\sin \left(\theta\right)\). Is she correct? Explain.
-
Piyali says that \(\tan \left(\theta+\frac{\pi}{4}\right)=\frac{1+\tan \left(\theta\right)}{1-\tan \left(\theta\right)}\). Is she correct? Explain.
Basic Skills
-
Show that \(\cos \left(45^{\circ}+45^{\circ}\right)\) is not equal to \(\cos \left(45^{\circ}\right)+\cos \left(45^{\circ}\right)\).
-
Show that \(\tan \left(60^{\circ}-30^{\circ}\right)\) is not equal to \(\tan \left(60^{\circ}\right)-\tan \left(30^{\circ}\right)\).
-
Use your calculator to verify that \(\tan \left(87^{\circ}-29^{\circ}\right)\) is not equal to \(\tan \left(87^{\circ}\right)-\tan \left(29^{\circ}\right)\).
-
Use your calculator to verify that \(\cos \left(52^{\circ}+64^{\circ}\right)\) is not equal to \(\cos \left(52^{\circ}\right)+\cos \left(64^{\circ}\right)\).
-
Use graphs to show that \(\sin \left(x-\frac{\pi}{6}\right)\) is not equivalent to \(\sin \left(x\right)-\sin \left(\frac{\pi}{6}\right)\).
-
Use graphs to show that \(\tan \left(x+\frac{\pi}{4}\right)\) is not equivalent to \(\tan \left(x\right)+\tan \left(\frac{\pi}{4}\right)\).
For Problems 10 - 30, use the Sum and Difference Identities to find the exact value. You may have need of the Ratio, Reciprocal, or Symmetry Identities as well.
-
\(\cos(15^{\circ})\)
-
\(\sin(15^{\circ})\)
-
\(\tan(15^{\circ})\)
-
\(\cos(75^{\circ})\)
-
\(\cos(165^{\circ})\)
-
\(\sin(165^{\circ})\)
-
\(\sec(165^{\circ})\)
-
\(\sin(105^{\circ})\)
-
\(\csc(195^{\circ})\)
-
\(\cot(255^{\circ})\)
-
\(\tan(375^{\circ})\)
-
\(\cos\left(\dfrac{13\pi}{12}\right)\)
-
\(\sin\left(\dfrac{11\pi}{12}\right)\)
-
\(\tan\left(\dfrac{13\pi}{12}\right)\)
-
\(\cos \left( \dfrac{7\pi}{12} \right)\)
-
\(\tan \left( \dfrac{17\pi}{12} \right)\)
-
\(\sin \left( \dfrac{\pi}{12} \right)\)
-
\(\cot \left( \dfrac{11\pi}{12} \right)\)
-
\(\csc \left( \dfrac{5\pi}{12} \right)\)
-
\(\sec \left( -\dfrac{\pi}{12} \right)\)
-
\(\sin\left(\dfrac{29\pi}{12}\right)\)
For Problems 31 - 34, find the exact value of the expression without using a calculator.
-
\(\cos\left(-10^\circ\right)\cos\left(35^\circ\right) + \sin\left(-10^\circ\right)\sin\left(35^\circ\right)\)
-
\(\cos\left(\dfrac{7\pi}{9}\right)\cos\left(\dfrac{2\pi}{9}\right) - \sin\left(\dfrac{7\pi}{9}\right)\sin\left(\dfrac{2\pi}{9}\right)\)
-
\(\sin\left(\dfrac{7\pi}{9}\right)\cos\left(\dfrac{2\pi}{9}\right) + \cos\left(\dfrac{7\pi}{9}\right)\sin\left(\dfrac{2\pi}{9}\right)\)
-
\(\sin(80^\circ)\cos(55^\circ) + \cos(80^\circ)\sin(55^\circ)\)
For Problems 35 - 46, find exact values for the trigonometric ratios. (Do not use a calculator!)
-
Suppose \(\cos \left(\alpha\right) = \dfrac{3}{5}, \sin \left(\alpha\right) = \dfrac{4}{5}, \cos \left(\beta\right) = \dfrac{5}{13}\), and \(\sin \left(\beta\right) = \dfrac{-12}{13}\). Evaluate the following.
-
\(\cos (\alpha + \beta )\)
-
\(\sin (\alpha + \beta )\)
-
\(\tan (\alpha + \beta )\)
-
-
Suppose \(\cos \left(\alpha\right) = \dfrac{-2}{3}, \sin \left(\alpha\right) = \dfrac{\sqrt{5}}{3}, \cos \left(\beta\right) = \dfrac{\sqrt{3}}{2}\), and \(\sin \left(\beta\right) = \dfrac{-1}{2}\). Evaluate the following.
-
\(\cos (\alpha - \beta )\)
-
\(\sin (\alpha - \beta )\)
-
\(\tan (\alpha - \beta )\)
-
-
If \(\tan \left(t\right) = \dfrac{3}{4}\) and \(\tan\left( s\right) = \dfrac{-7}{24}\), find exact values for the following.
-
\(\tan (s + t)\)
-
\(\tan (s - t)\)
-
-
If \(\tan \left(x\right) = -3\) and \(\tan \left(y\right) = -5\), find exact values for the following.
-
\(\tan (x + y)\)
-
\(\tan (x - y)\)
-
-
Suppose \(\cos \left(\theta\right) = \dfrac{15}{17}\) and \(\sin \left(\phi\right) = \dfrac{3}{5}\), where \(\theta\) and \(\phi\) are in quadrant I. Evaluate the following.
-
\(\cos (\theta + \phi )\)
-
\(\tan (\theta - \phi )\)
-
-
Suppose \(\cos \left(\theta\right) = \dfrac{15}{17}\), where \(\theta\) is in quadrant IV, and \(\sin \left(\phi\right) = \dfrac{3}{5}\), where \(\phi\) is in quadrant II. Evaluate the following.
-
\(\sin (\theta - \phi )\)
-
\(\tan (\theta + \phi )\)
-
-
If \(\sin \left(\alpha\right) = \dfrac{12}{13}, \dfrac{\pi}{2} < \alpha < \pi\), and \(\cos \left(\beta\right) = \dfrac{-3}{5}, \pi < \beta < \dfrac{3\pi}{2}\), find exact values for the following.
-
\(\sin (\alpha + \beta )\)
-
\(\cos (\alpha + \beta )\)
-
\(\tan (\alpha + \beta )\)
-
Sketch the angles \(\alpha, \beta\) and \(\alpha + \beta\).
-
-
If \(\cos \left(\alpha\right) = \dfrac{3}{8}, \dfrac{3\pi}{2} < \alpha < 2\pi\), and \(\sin \left(\beta\right) = \dfrac{-1}{4}, \pi < \beta < \dfrac{3\pi}{2}\), find exact values for the following.
-
\(\sin (\alpha - \beta )\)
-
\(\cos (\alpha - \beta )\)
-
\(\tan (\alpha - \beta )\)
-
Sketch the angles \(\alpha, \beta\) and \(\alpha - \beta\).
-
-
If \(\alpha\) is a Quadrant IV angle with \(\cos(\alpha) = \dfrac{\sqrt{5}}{5}\), and \(\sin(\beta) = \dfrac{\sqrt{10}}{10}\), where \(\dfrac{\pi}{2} < \beta < \pi\), find
-
\(\cos(\alpha + \beta)\)
-
\(\sin(\alpha + \beta)\)
-
\(\tan(\alpha + \beta)\)
-
\(\cos(\alpha - \beta)\)
-
\(\sin(\alpha - \beta)\)
-
\(\tan(\alpha - \beta)\)
-
-
If \(\csc(\alpha) = 3\), where \(0 < \alpha < \dfrac{\pi}{2}\), and \(\beta\) is a Quadrant II angle with \(\tan(\beta) = -7\), find
-
\(\cos(\alpha + \beta)\)
-
\(\sin(\alpha + \beta)\)
-
\(\tan(\alpha + \beta)\)
-
\(\cos(\alpha - \beta)\)
-
\(\sin(\alpha - \beta)\)
-
\(\tan(\alpha - \beta)\)
-
-
If \(\sin(\alpha) = \dfrac{3}{5}\), where \(0 < \alpha < \dfrac{\pi}{2}\), and \(\cos(\beta) = \dfrac{12}{13}\) where \(\dfrac{3\pi}{2} < \beta < 2\pi\), find
-
\(\sin(\alpha + \beta)\)
-
\(\cos(\alpha - \beta)\)
-
\(\tan(\alpha - \beta)\)
-
-
If \(\sec(\alpha) = -\dfrac{5}{3}\), where \(\dfrac{\pi}{2} < \alpha < \pi\), and \(\tan(\beta) = \dfrac{24}{7}\), where \(\pi < \beta < \dfrac{3\pi}{2}\), find
-
\(\csc(\alpha - \beta)\)
-
\(\sec(\alpha + \beta)\)
-
\(\cot(\alpha + \beta)\)
-
-
If \(\sin \left(\theta\right)=0.2\) and \(\cos \left(\theta\right)>0\), find \(\sin \left(\theta+\frac{\pi}{3}\right)\).
-
If \(\cos \left(\theta\right)=0.6\) and \(\sin \left(\theta\right)<0\), find \(\cos \left(\theta+\frac{3 \pi}{4}\right)\).
For Problems 49 - 54, use the Sum and Difference Identities to expand each expression. Simplify your answers completely.
-
\(\sin \left(\theta-270^{\circ}\right)\)
-
\(\cos \left(270^{\circ}+\theta\right)\)
-
\(\cos \left(t+\frac{\pi}{6}\right)\)
-
\(\sin \left(t-\frac{2 \pi}{3}\right)\)
-
\(\tan \left(\beta-\frac{\pi}{6}\right)\)
-
\(\tan \left(\phi+\frac{\pi}{4}\right)\)
-
Use the Sum Identities for sine and cosine to derive a formula for each expression. Then use graphs to verify your formula.
-
\(\cos (\theta + 90^{\circ})\)
-
\(\sin (\theta + 90^{\circ})\)
-
-
Use the Sum Identities for sine and cosine to derive a formula for each expression. Then use graphs to verify your formula.
-
\(\cos (\theta+\pi)\)
-
\(\sin (\theta+\pi)\)
-
-
Use the Difference Identities for sine and cosine to derive formulas for the following.
-
\(\cos \left(\theta-\dfrac{\pi}{2}\right)\)
-
\(\sin \left(\theta-\dfrac{\pi}{2}\right)\)
-
For Problems 58 - 61, graph one cycle of the function by hand.
-
\( f(x) = \sin\left( 4x \right) \cos\left( 3x \right) - \cos\left( 4x \right)\sin\left( 3x \right) \)
-
\( f(x) = \sin\left( x \right) \cos\left( 2x \right) + \cos\left( 2x \right)\sin\left( x \right) \)
-
\( f(x) = \frac{1}{5} \cos\left( 5x \right) \cos\left( 2x \right) + \frac{1}{5}\sin\left( 5x \right)\sin\left( 2x \right) \)
-
\( f(x) = 2 \cos\left( x \right) \cos\left( 2x \right) - 2\sin\left( x \right)\sin\left( 2x \right) \)
Synthesis Questions
For Problems 62 - 67, simplify the function using the Sum and Difference Identities.
-
\(f(x)=\sin\left(x+\dfrac{\pi}{2}\right)\)
-
\(f(x)=\cos\left(x-\dfrac{\pi}{4}\right)\)
-
\(f(x)=\tan\left(\pi-x\right)\)
-
\(f(x)=\sin\left(\dfrac{\pi}{6}-x\right)\)
-
\(f(x)=\cos\left(x+\dfrac{11\pi}{12}\right)\)
-
\(f(x)=\cos\left(\dfrac{2\pi}{3}-x\right)\)
For Problems 68 - 74,
(a) Use graphs to decide if the equation is an identity.
(b) If the equation is not an identity, find a value of the variable that makes the equation false.
-
\(\sin \left(\dfrac{\pi}{2}+\beta\right)=1+\sin \left(\beta\right)\)
-
\(\cos \left(\dfrac{\pi}{3}-\beta\right)=\cos \left(\beta-\dfrac{\pi}{3}\right)\)
-
\(\sin \left(A+180^{\circ}\right)=-\sin \left(A\right)\)
-
\(\cos \left(\phi+\dfrac{\pi}{3}\right)=\dfrac{1}{2}+\cos \left(\phi\right)\)
-
\(\sin \left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(\sin \left(x\right)+\cos \left(x\right)\right)\)
-
\(2 \cos \left(x-\dfrac{\pi}{6}\right)=\sin \left(x\right)+\sqrt{3} \cos \left(x\right)\)
-
\(\sin \left(x-\dfrac{\pi}{3}\right)+\cos \left(x+\dfrac{\pi}{6}\right)=0\)
-
-
Use a graphing device to draw the graph of \(f(x) = \sin(x) + \cos(x)\) using \(-\pi \leq x \leq 2\pi\) and \(-2 \leq y \leq 2\). Does the graph of this function appear to be a sinusoid? If so, approximate the amplitude and phase shift of the sinusoid. What is the period of this sinusoid.
-
Use one of the sum identities to rewrite the expression \(\sin\left(x + \frac{\pi}{4}\right)\). Then use the values of \(\sin\left(\frac{\pi}{4}\right)\) and \(\cos\left(\frac{\pi}{4}\right)\) to further rewrite the expression.
-
Use the result from part (b) to show that the function \(f(x) = \sin(x) + \cos(x)\) is indeed a sinusoidal function. What is its amplitude, phase shift, and period?
-
-
-
Use a graphing device to draw the graph of \(g(x) = \sin(x) + \sqrt{3}\cos(x)\) using \(-\pi \leq x \leq 2\pi\) and \(-2.5 \leq y \leq 2.5\). Does the graph of this function appear to be a sinusoid? If so, approximate the amplitude and phase shift of the sinusoid. What is the period of this sinusoid.
-
Use one of the sum identities to rewrite the expression \(\sin\left(x + \frac{\pi}{3}\right)\). Then use the values of \(\sin\left(\frac{\pi}{3}\right)\) and \(\cos\left(\frac{\pi}{3}\right)\) to further rewrite the expression.
-
Use the result from part (b) to show that the function \(g(x) = \sin(x) + \sqrt{3}\cos(x)\) is indeed a sinusoidal function. What is its amplitude, phase shift, and period?
-
Proofs
-
Use the Difference Identities for sine and cosine to prove the statement.
-
\(\cos \left(\dfrac{\pi}{2}-\theta\right)=\sin \left(\theta\right)\)
-
\(\sin \left(\dfrac{\pi}{2}-\theta\right)=\cos \left(\theta\right)\)
-
In Exercises 78 - 98, prove the identity.
-
\(\cos(\theta - \pi) = -\cos(\theta)\)
-
\(\sin(\pi - \theta) = \sin(\theta)\)
-
\(\tan\left(\theta + \dfrac{\pi}{2} \right) = -\cot(\theta)\)
-
\(\sin(\alpha + \beta) + \sin(\alpha - \beta) = 2\sin(\alpha)\cos(\beta)\)
-
\(\sin(\alpha + \beta) - \sin(\alpha - \beta) = 2\cos(\alpha) \sin(\beta)\)
-
\(\cos(\alpha + \beta) + \cos(\alpha - \beta) = 2\cos(\alpha) \cos(\beta)\)
-
\(\cos(\alpha + \beta) - \cos(\alpha - \beta) = -2\sin(\alpha) \sin(\beta)\)
-
\(\dfrac{\sin(\alpha+\beta)}{\sin(\alpha-\beta)} = \dfrac{1+\cot(\alpha) \tan(\beta)}{1 - \cot(\alpha) \tan(\beta)}\)
-
\(\dfrac{\cos(\alpha + \beta)}{\cos(\alpha - \beta)} = \dfrac{1 - \tan(\alpha)\tan(\beta)}{1 + \tan(\alpha)\tan(\beta)}\)
-
\(\dfrac{\tan(\alpha + \beta)}{\tan(\alpha - \beta)} = \dfrac{\sin(\alpha)\cos(\alpha) + \sin(\beta)\cos(\beta)}{\sin(\alpha)\cos(\alpha) - \sin(\beta)\cos(\beta)}\)
-
\(\dfrac{\sin(t + h) - \sin(t)}{h} = \cos(t) \left(\dfrac{\sin(h)}{h} \right) + \sin(t) \left( \dfrac{\cos(h) - 1}{h} \right)\)
-
\(\dfrac{\cos(t + h) - \cos(t)}{h} = \cos(t) \left( \dfrac{\cos(h) - 1}{h} \right) - \sin(t) \left(\dfrac{\sin(h)}{h} \right)\)
-
\(\dfrac{\tan(t + h) - \tan(t)}{h} = \left( \dfrac{\tan(h)}{h} \right) \left(\dfrac{\sec^{2}(t)}{1 - \tan(t)\tan(h)} \right)\)
-
\(\cot\left(A+B\right) = \dfrac{\cot\left(A\right)\cot\left(B\right) - 1}{\cot\left(A\right) + \cot\left(B\right)}\)
-
\(\cot\left(A-B\right) = \dfrac{\cot\left(A\right)\cot\left(B\right) + 1}{\cot\left(B\right) - \cot\left(A\right)}\)
-
\(\tan\left(\theta + 45^{\circ}\right) = \dfrac{1 + \tan\left(\theta\right)}{1 - \tan\left(\theta\right)}\)
-
\(\dfrac{\cos\left(A+B\right)}{\sin\left(A\right)\cos\left(B\right)} = \cot\left(A\right) - \tan\left(B\right)\)
-
\(\cot\left(A\right) + \cot\left(B\right) = \dfrac{\sin\left(A+B\right)}{\sin\left(A\right)\sin\left(B\right)}\)
-
\(\dfrac{\sin\left(A-B\right)}{\sin\left(A+B\right)} = \dfrac{\cot\left(B\right) - \cot\left(A\right)}{\cot\left(B\right) + \cot\left(A\right)}\)
-
\(\cos\left(A+B+C\right) = \cos\left(A\right)\cos\left(B\right)\cos\left(C\right) - \cos\left(A\right)\sin\left(B\right)\sin\left(C\right) - \sin\left(A\right)\cos\left(B\right)\sin\left(C\right) - \sin\left(A\right)\sin\left(B\right)\cos\left(C\right)\)
-
\(\tan\left(A+B+C\right) = \dfrac{\tan\left(A\right) + \tan\left(B\right) + \tan\left(C\right) - \tan\left(A\right)\tan\left(B\right)\tan\left(C\right)}{1 - \tan\left(B\right)\tan\left(C\right) - \tan\left(A\right)\tan\left(C\right) - \tan\left(A\right)\tan\left(B\right)}\)
-
Verify the Cofunction Identities for tangent, secant, cosecant and cotangent.
-
Verify the Difference Identities for sine and tangent.
Challenge Problems
-
Prove the identity\[\sin\left(\theta\right) + \cos\left(\theta\right) = \sqrt{2}\sin\left(\theta + 45^{\circ}\right).\nonumber \]Explain why this shows that\[ -\sqrt{2} \leq \sin\left(\theta\right) + \cos\left(\theta\right) \leq \sqrt{2}\nonumber \]for all angles \(\theta \). For which \(\theta \) between \(0^{\circ} \) and \(360^{\circ} \) would \(\sin\left(\theta\right)+ \cos\left(\theta\right) \) be the largest?
Problems 102 and 103 verify the Addition and Subtraction Identities for acute angles.
-
The figure below shows a right triangle inscribed in a rectangle.

-
Label the legs \(l_1\) and \(l_2\) of the right triangle with their lengths.
-
Explain why \(\theta_1=\beta\) and \(\theta_2=\alpha+\beta\). Label the diagram with these angles.
-
Label the legs \(s_1\) and \(s_2\) of the bottom triangle with their lengths.
-
Label the legs \(s_3\) and \(s_4\) of the top left triangle with their lengths.
-
Label the legs \(s_5\) and \(s_6\) of the top right triangle with their lengths.
-
Use the fact that the opposite sides of a rectangle are equal to state the addition formulas for sine and cosine.
-
-
The figure below shows a right triangle inscribed in a rectangle.

-
Label the legs \(l_1\) and \(l_2\) of the right triangle with their lengths.
-
Explain why \(\theta_1=\beta\) and \(\theta_2=\alpha-\beta\). Label the diagram with these angles.
-
Label the legs \(s_1\) and \(s_2\) of the bottom triangle with their lengths.
-
Label the legs \(s_3\) and \(s_4\) of the top left triangle with their lengths.
-
Label the legs \(s_5\) and \(s_6\) of the top right triangle with their lengths.
-
Use the fact that the opposite sides of a rectangle are equal to state the subtraction formulas for sine and cosine.
-
-
Follow the steps to prove the difference of angles formula for cosine,\[\cos (\alpha-\beta)=\cos \left(\alpha\right) \cos \left(\beta\right)+\sin \left(\alpha\right) \sin \left(\beta\right)\nonumber \]
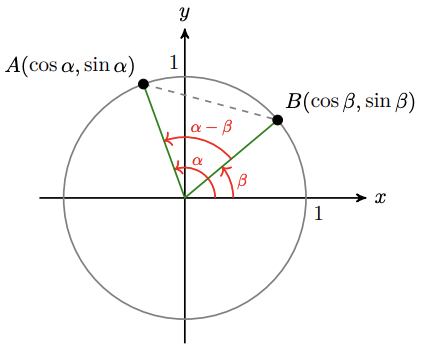
-
Write an expression for \((A B)^2\), the square of the distance between the points \(A\) and \(B\), using the Law of Cosines for \(\triangle A O B\).
-
Write another expression for \((A B)^2\) using the Distance Formula and the coordinates of \(A\) and \(B\).
-
Equate the two expressions for \((A B)^2\) you obtained in (a) and (b). Simplify the equation to obtain \(\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
-
-
For any positive angles \(A \), \(B \), and \(C \) such that \(A+B+C=90^{\circ} \), show that\[ \tan\left(A\right)\tan\left(B\right) + \tan\left(B\right)\tan\left(C\right) + \tan\left(C\right)\tan\left(A\right) = 1. \nonumber \]
-
Prove the identity\[\sin\left(A+B\right)\cos\left(B\right) - \cos\left(A+B\right)\sin\left(B\right) = \sin\left(A\right). \nonumber \]Note that the right side depends only on \(A \), while the left side depends on both \(A \) and \(B \).
-
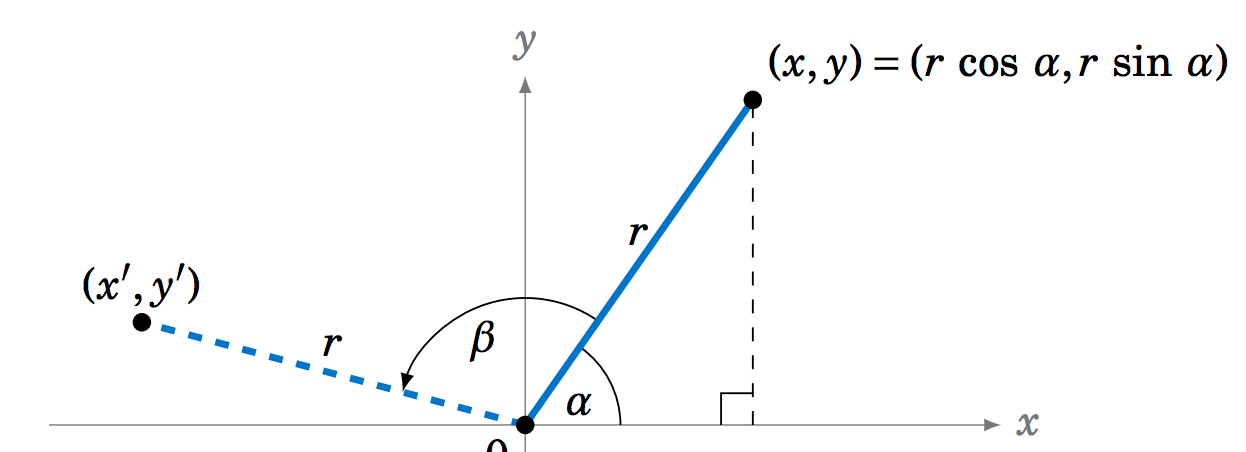
A line segment of length \(r > 0 \) from the origin to the point \((x,y) \) makes an angle \(\alpha \) with the positive \(x\)-axis, so that \((x,y) = \left(r\cos\left(\alpha\right), r\sin\left(\alpha\right)\right) \), as in the figure below. What are the endpoint's new coordinates \((x^{\prime},y^{\prime}) \) after a counterclockwise rotation by an angle \(\beta\)? Your answer should be in terms of \(r \), \(\alpha \), and \(\beta \).