6.3: Double-Angle Identities

Learning Objectives

• Use a Double-Angle Identity to find the exact value of a trigonometric function.
• Prove an identity using a Double-Angle Identity.
• Use a Double-Angle Identity to graph an equation.

The Double Angle Identities

Several other useful identities can be derived from the Sum and Difference Identities. The Double-Angle Identities are a special case of the Sum Identities, where \(\alpha=\beta \). Deriving the Double-Angle Identity for sine begins with the Sum Identity,\[\sin(\alpha+\beta)=\sin \left(\alpha\right) \cos \left(\beta\right)+\cos \left(\alpha\right) \sin \left(\beta\right). \nonumber \]If we let \(\alpha=\beta=\theta\), then we have\[\begin{array}{rrcl}
& \sin(\theta+\theta) & = & \sin \left(\theta\right) \cos \left(\theta\right)+\cos \left(\theta\right) \sin \left(\theta\right) \\
\implies & \sin(2\theta) & = & 2\sin \left(\theta\right) \cos \left(\theta\right) \\
\end{array} \nonumber \]Deriving the Double-Angle Identity for cosine gives us three options. First, starting from the Sum Identity,\[\cos(\alpha+\beta)=\cos \left(\alpha\right) \cos \left(\beta\right) - \sin \left(\alpha\right) \sin \left(\beta\right),\nonumber \]and letting \(\alpha=\beta=\theta\), we have\[\begin{array}{rrcl}
& \cos(\theta+\theta) & = & \cos \left(\theta\right) \cos \left(\theta\right)-\sin \left(\theta\right) \sin \left(\theta\right) \\
\implies & \cos(2\theta) & = & \cos^2 \left(\theta\right) - \sin^2 \left(\theta\right) \\
\end{array} \nonumber \]Using the Pythagorean Identities, we can expand this Double-Angle Identity for cosine and get two more variations. The first variation is\[\begin{array}{rcl}
\cos(2\theta) & = & \cos^2 \left(\theta\right) - \sin^2 \left(\theta\right) \\
& = & \left(1-\sin^2 \left(\theta\right)\right)-\sin^2 \left(\theta\right) \\
& = & 1 - 2 \sin^2\left( \theta \right) \\
\end{array}\nonumber \]The second variation is\[\begin{array}{rcl}
\cos(2\theta) & = & \cos^2 \left(\theta\right)-\sin^2 \left(\theta\right) \\
& = & \cos^2 \left(\theta\right)-\left(1-\cos^2 \left(\theta\right)\right) \\
& = & 2 \cos^2 \left(\theta\right)-1 \\
\end{array} \nonumber \]Similarly, to derive the Double-Angle Identity for the tangent, replacing \(\alpha=\beta=\theta\) in the sum formula gives\[\begin{array}{rrcl}
& \tan(\alpha+\beta) & = & \dfrac{\tan \left(\alpha\right)+\tan \left(\beta\right)}{1-\tan \left(\alpha\right) \tan \left(\beta\right)} \\
\\
\implies & \tan(\theta+\theta) & = & \dfrac{\tan \left(\theta\right)+\tan \left(\theta\right)}{1-\tan \left(\theta\right) \tan \left(\theta\right)} \\
\\
\implies & \tan(2\theta) & = & \dfrac{2\tan \left(\theta\right)}{1-\tan^2 \left(\theta\right)} \\
\end{array} \nonumber \]The next theorem summarizes all of this work.

Theorem: Double-Angle Identities

\[ \begin{array}{rcl}
\sin\left( 2\theta \right) & = & 2 \sin\left( \theta \right) \cos\left( \theta \right) \\
\\
\cos\left( 2\theta \right) & = & \cos^2\left( \theta \right) - \sin^2\left( \theta \right) \\
& = & 2\cos^2\left( \theta \right) - 1 \\
& = & 1 - 2 \sin^2\left( \theta \right) \\
\\
\tan\left( 2\theta \right) & = & \dfrac{2 \tan\left( \theta \right)}{1 - \tan^2\left( \theta \right)} \\
\end{array} \nonumber \]

Advice: Memorize The Sine and Cosine Versions of These Identities

The Double-Angle Identities for the sine and cosine are needed throughout the rest of Trigonometry, Calculus, and Differential Equations. While not as prevalent as the Pythagorean Theorem or the Quadratic Formula, the need to commit them to memory and their importance cannot be overstated. The tangent version is less common and can be derived from the sine and cosine versions if needed.

You can also justify the identities to yourself by graphing both sides of the formula to see that the graphs are identical.

Caution: Don't Factor Out of Functions!

The first thing we can learn from the Double-Angle Identities is that \(\sin \left(2 \theta\right)\) is not equal to \(2 \sin \left(\theta\right)\)! You can check this very easily by choosing a value for \(\theta\), say \(45^{\circ}\). Then\[\sin \left(2 \theta\right) = \sin \left(90^{\circ}\right)=1 \nonumber \]but\[ 2 \sin \left(\theta\right)=2 \sin \left(45^{\circ}\right)=2\left(\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}\nonumber \]and \(\sqrt{2} \neq 1\). Similarly, \(\cos \left(2 \theta\right) \neq 2 \cos \left(\theta\right)\) and \(\tan \left(2 \theta\right) \neq 2 \tan \left(\theta\right)\).

Finding Exact Values of Trigonometric Functions Involving Double Angles

We now reach a point in Trigonometry where we are told the value of a trigonometric function of \( \theta \), but we are interested in the value of a trigonometric function of \( 2 \theta \). In these instances, the Double-Angle Identities (which, again, are special sub-cases of the Sum and Difference Identities) are what we need.

Example \( \PageIndex{ 1 } \)

Find \(\sin \left(2 \theta\right)\) for the angle \(\theta\) shown.

Solution

We start by using the Pythagorean Theorem to find the hypotenuse of the triangle.\[c^2=2^2+3^2=13\nonumber \]so \(c=\sqrt{13}\). Thus, \(\cos \left(\theta\right)=\frac{3}{\sqrt{13}}\) and \(\sin \left(\theta\right)=\frac{2}{\sqrt{13}}\). Now we can use these values in the Double-Angle Identity to find \(\sin \left(2 \theta\right)\).\[\begin{array}{rcl}
\sin \left(2 \theta\right) & = & 2 \sin \left(\theta\right) \cos \left(\theta\right) \\
\\
& = & 2\left(\dfrac{2}{\sqrt{13}}\right)\left(\dfrac{3}{\sqrt{13}}\right) \\
\\
& = & \dfrac{12}{13} \\
\end{array}\nonumber \]

Checkpoint \( \PageIndex{ 1 } \)

Find \(\cos \left(2 \theta\right)\) and \(\tan \left(2 \theta\right)\) for the angle \(\theta\) shown in Example \( \PageIndex{ 1 } \).

Answer

\(\cos \left(2 \theta\right)=\dfrac{5}{13}, \quad \tan \left(2 \theta\right)=\dfrac{12}{5}\)

Example \(\PageIndex{2}\)

Given that \(\cot\left(\theta\right)=−\frac{3}{4}\) and \(\theta\) is in quadrant II, find the following:

1. \(\sin(2\theta)\)
2. \(\cos(2\theta)\)
3. \(\tan(2\theta)\)

Solutions

If we draw a triangle to reflect the information given, we can find the values needed to help us. We are given \(\cot\left(\theta\right)=−\frac{3}{4}\), such that \(\theta\) is in quadrant II. The cotangent of an angle is equal to the adjacent side over the opposite side, and because \(\theta\) is in the second quadrant, the adjacent side is on the \( x \)-axis and is negative. We use the Pythagorean Theorem to find the length of the hypotenuse:\[\begin{array}{rrcl}
& {(-4)}^2+{(3)}^2 & = & c^2 \\
\implies & 16+9 & = & c^2\\
\implies & 25 & = & c^2 \\
\implies & c & = & 5 \\
\end{array}\nonumber \]Now we can draw the situation appropriately.

(not drawn to scale)

When drawn like this, you can use the coordinate definition of the trigonometric functions or the right triangle definition using \( \hat{\theta} \) and the fact that \( \theta \) terminates in \( \mathrm{QII} \) - it's your choice.

1. Let’s begin by writing the Double-Angle Identity for sine.\[\sin\left(2\theta\right)=2 \sin\left(\theta\right) \cos\left(\theta\right)\nonumber \]We see that we to need to find \(\sin\left(\theta\right)\) and \(\cos\left(\theta\right)\). Based on our drawing, we see that the hypotenuse equals \(5\), so \(\sin\left(\theta\right) = \frac{4}{5}\), and \(\cos\left(\theta\right) = -\frac{3}{5}\). Substitute these values into the equation and simplify.Thus,\[\begin{array}{rcl}
   \sin\left(2\theta\right) & = & 2 \left(\dfrac{4}{5}\right)\left(-\dfrac{3}{5}\right) \\
   \\
   & = & -\dfrac{24}{25} \\
   \end{array} \nonumber \]
2. Write the Double-Angle Identity for cosine.\[\cos\left(2\theta\right)=\cos^2\left(\theta\right) - \sin^2\left(\theta\right) \nonumber \]Again, substitute the values of the sine and cosine into the equation and simplify.\[\begin{array}{rcl}
   \cos\left(2\theta\right) & = & \left(-\dfrac{3}{5}\right)^2 - \left(\dfrac{4}{5}\right)^2 \\
   \\
   & = & \dfrac{9}{25} - \dfrac{16}{25} \\
   \\
   & = & -\dfrac{7}{25} \\
   \end{array} \nonumber \]
3. Write the Double-Angle Identity for tangent.\[\tan\left(2\theta\right)=\dfrac{2 \tan\left(\theta\right)}{1−\tan^2\left(\theta\right)}\nonumber \]In this formula, we need the tangent. Using the Reciprocal Identity, we have \(\tan \left(\theta\right)=-\dfrac{4}{3}\). Substitute this value into the equation, and simplify.\[\begin{array}{rcl}
   \tan\left(2\theta\right) & = & \dfrac{2\left(-\dfrac{4}{3}\right )}{1-\left(-\dfrac{4}{3}\right)^2} \\
   \\
   & = & \dfrac{-\dfrac{8}{3}}{1-\dfrac{16}{9}} \\
   \\
   & = & -\dfrac{8}{3}\left(-\dfrac{9}{7}\right) \\
   \\
   & = & \dfrac{24}{7} \\
   \end{array} \nonumber \]

A note about Example \( \PageIndex{ 2c } \) is in order. As we have seen throughout Trigonometry, several ways to approach a problem usually exist. It's easy to get so intent on using one method with a problem that we blind ourselves to simpler approaches. For example, we could have used the Ratio Identities to get\[ \tan\left( 2\theta \right) = \dfrac{\sin\left( 2\theta \right)}{\cos\left( 2\theta \right)} = \dfrac{-24/25}{-7/25} = \dfrac{24}{7}. \nonumber \]

Checkpoint \(\PageIndex{2}\)

Given \(\sin\left(\alpha\right)=\frac{5}{8}\), with \(\theta\) in quadrant I, find \(\cos(2\alpha)\). 

Answer

\(\cos(2\alpha)=\dfrac{7}{32}\)

We can work with algebraic expressions instead of numerical values for the trigonometric ratios.

Example \( \PageIndex{ 3 } \)

Use the figure to express \(\cos \left(2 \phi\right)\) in terms of \(a\).

Solution

We use the Pythagorean Theorem to find an expression for the third side of the triangle.\[\begin{array}{rrcl}
& a^2+b^2 & = & 3^2 \\
\implies & b & = & \sqrt{9-a^2} \\
\end{array} \nonumber \]Now we can write expressions for the sine and cosine of \(\phi\).\[\cos \left(\phi\right)=\dfrac{a}{3} \quad \text { and } \quad \sin \left(\phi\right)=\dfrac{\sqrt{9-a^2}}{3}\nonumber \]Finally, we substitute these expressions into the Double-Angle Identity.\[\begin{array}{rcl}
\cos \left(2 \phi\right) & = & \cos ^2 \left(\phi\right)-\sin ^2 \left(\phi\right) \\
\\
& = & \left(\dfrac{a}{3}\right)^2-\left(\dfrac{\sqrt{9-a^2}}{3}\right)^2 \\
\\
& = & \dfrac{a^2}{9}-\dfrac{9-a^2}{9} \\
\\
& = & \dfrac{2a^2-9}{9} \\
\end{array}\nonumber \]

Checkpoint \( \PageIndex{ 3 } \)

For the triangle in Example \( \PageIndex{ 2 } \), find expressions for \(\sin \left(2 \phi\right)\) and \(\tan \left(2 \phi\right)\).

Answer

\(\sin \left(2 \phi\right)=\dfrac{2 a \sqrt{9-a^2}}{9}, \quad \tan \left(2 \phi\right)=\dfrac{2 a \sqrt{9-a^2}}{2 a^2-9}\)

Example \( \PageIndex{ 4 } \)

Find an expression for \(\cos \left(2 \beta\right)\) if you know that \(\cos \left(\beta\right)=\frac{x}{4}\).

Solution

We use the identity \(\cos \left(2 \theta\right)=2 \cos ^2 \left(\theta\right)-1\).\[\begin{array}{rcl}
\cos \left(2 \beta\right) & = & 2 \cos ^2 \left(\beta\right)-1 \\
\\
& = & 2\left(\dfrac{x}{4}\right)^2-1 \\
\\
& = & \dfrac{2 x^2}{16}-1 \\
\\
& = & \dfrac{2 x^2-16}{16} \\
\\
& = & \dfrac{x^2-8}{8} \\
\end{array}\nonumber \]

Checkpoint \( \PageIndex{ 4 } \)

Find an expression for \(\cos \left(2 \alpha\right)\) if you know that \(\sin \left(\alpha\right)=\frac{6}{w}\).

Answer

\(\dfrac{w^2-76}{w^2}\)

Revisiting Proofs of Identities

Establishing identities using the Double-Angle Identities is performed using the same steps we used previously.

Example \(\PageIndex{5}\)

Verify the following identity.\[1+\sin\left(2\theta\right)=\left(\sin\left(\theta\right)+\cos\left(\theta\right)\right)^2 \nonumber \]

Solution

We will work on the right side of the equal sign and rewrite the expression until it matches the left side.\[\begin{array}{rclcl}
\text{RHS} & = & \left(\sin \left(\theta\right)+\cos \left(\theta\right)\right)^2 & & \\
& = & \sin^2 \left(\theta\right) +2 \sin \left(\theta\right) \cos \left(\theta\right)+\cos^2 \left(\theta\right) & \quad & \left( \text{distribution} \right) \\
& = & \left(\sin^2 \left(\theta\right)+\cos^2 \left(\theta\right)\right)+2 \sin\left( \theta \right)\cos \left(\theta\right) & \quad & \left( \text{Commutative and Associative Properties of Addition} \right) \\
& = & 1+2 \sin \left(\theta\right) \cos \left(\theta\right) & \quad & \left( \text{Pythagorean Identities} \right) \\
& = & 1+\sin\left(2\theta\right) & \quad & \left( \text{Double-Angle Identities} \right) \\
& = & \text{LHS} & & \\
\end{array} \nonumber \]

The process in Example \( \PageIndex{ 5 } \) is not complicated, as long as we recall the perfect square formula from algebra:\[{(a\pm b)}^2=a^2\pm 2ab+b^2, \nonumber \]where \(a=\sin \left(\theta\right)\) and \(b=\cos \left(\theta\right)\). Part of being successful in Mathematics is the ability to recognize patterns. While the terms or symbols may change, the Algebra remains consistent.

Checkpoint \(\PageIndex{5}\)

Verify the identity.\[\cos^4 \left(\theta\right)-\sin^4 \left(\theta\right) =\cos\left(2\theta\right).\nonumber \] 

Answer

\(\cos^4 \left(\theta\right)−\sin^4 \left(\theta\right)=\left(\cos^2 \left(\theta\right)-\sin^2 \left(\theta\right)\right)\left(\cos^2\left( \theta\right)+\sin^2 \left(\theta\right)\right) = \cos\left(2\theta\right) \cdot 1 = \cos\left(2\theta\right)\)

Example \(\PageIndex{6}\)

Prove the identity.\[\tan\left(2 \theta\right)=\dfrac{2}{\cot \left(\theta\right)−\tan \left(\theta\right)}\nonumber \]

Solution

Despite the right side looking more complicated, the obvious Double-Angle Identity on the left side tells us that we should at least start on that side and simplify or rewrite until it equals the right side of the equation.\[\begin{array}{rclcl}
\text{LHS} & = & \tan\left(2\theta\right) & & \\
\\
& = & \dfrac{2 \tan \left(\theta\right)}{1-\tan^2\left( \theta\right)} & \quad & \left(\text{Double-Angle Identity}\right) \\
\\
& = & \dfrac{2 \tan \left(\theta\right)\left (\dfrac{1}{\tan \left(\theta\right)}\right)}{\left(1-\tan^2\left( \theta\right)\right)\left (\dfrac{1}{\tan \left(\theta\right)}\right )} & \quad & \left(\text{multiply by a term that results in desired numerator}\right) \\
\\
& = & \dfrac{2}{\dfrac{1}{\tan \left(\theta\right)}-\dfrac{ \tan^2 \left(\theta\right)}{\tan \left(\theta\right)}} & & \\
\\
& = & \dfrac{2}{\cot \left(\theta\right)-\tan \left(\theta\right)} & \quad & \left(\text {Reciprocal Identity}\right) \\
\\
& = & \text{RHS} & & \\
\end{array} \nonumber \]

In Example \( \PageIndex{ 6 } \), if we had chosen to work on the right side, we would have worked backward to arrive at the equivalency. While this is possible (and not too tricky), I like taking advantage of obvious identities. There are usually several paths to a desired result when using the identities to simplify a trigonometric expression or solve a trigonometric equation.

Checkpoint \(\PageIndex{6}\)

Prove the identity.\[\cos(2\theta)\cos \theta=\cos^3 \left(\theta\right)−\cos \left(\theta\right) \sin^2 \left(\theta\right)\nonumber \] 

Answer

\(\cos(2\theta)\cos\left(\theta\right)=\left(\cos^2\left(\theta\right)−\sin^2\left(\theta\right)\right)\cos\left(\theta\right)=\cos^3\left(\theta\right)−\cos\left(\theta\right)\sin^2\left(\theta\right)\)

Revisiting Graphs of Trigonometric Functions

As with the previous section, we use this opportunity to expand the types of trigonometric functions we can graph.

Example \(\PageIndex{7}\)

Graph the function.\[ f(x) = -8\cos^2\left( 3x \right) + 4 \nonumber \]

Solution

Careful observation and a little pre-factoring will reveal that this function contains a Double-Angle Identity.\[ \begin{array}{rclcl}
f(x) & = & -8\cos^2\left( 3x \right) + 4 & & \\
& = & -4\left( 2\cos^2\left( 3x \right) - 1 \right) & \quad & \left( \text{factoring out the GCF} \right)\\
& = & -4 \cos\left( 6x \right) & \quad & \left( \text{Double-Angle Identity} \right) \\
\end{array} \nonumber \]This is a reflected cosine function with amplitude \( 4 \), period \( \frac{\pi}{3} \), step size \( \frac{\pi}{12} \), and no phase shift or vertical shift.

Checkpoint \(\PageIndex{7}\)

Graph the function.\[ g(x) = \dfrac{6\tan\left( \frac{\pi}{4}x \right)}{1 - \tan^2\left( \frac{\pi}{4} x \right)} \nonumber \]

Answer

\( g(x) = 3 \tan\left( \frac{\pi}{2}x \right) \).

---

Homework

Concept Check

1. Provide an example to show that doubling an angle does not double its sine or cosine.

Basic Skills

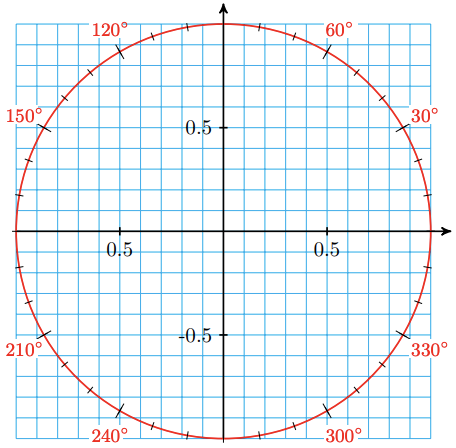
For Problems 2 - 5, use the unit circle to estimate trigonometric values. Then verify with your calculator.

2. Does \(\sin \left(2 \cdot 90^{\circ}\right) =2 \sin \left(90^{\circ}\right)\)?

3. Does \(\cos \left(2 \cdot 25^{\circ}\right)=2 \cos \left(25^{\circ}\right)\)?

4. Does \(\tan \left(2 \cdot 70^{\circ}\right)=2 \tan \left(70^{\circ}\right)\)?

5. Does \(\tan \left(2 \cdot 100^{\circ}\right)=2 \tan \left(100^{\circ}\right)\)?

For Problems 6 - 9, verify that each statement is true

6. \(\sin \left(90^{\circ}\right)=2 \sin \left(45^{\circ}\right) \cos \left(45^{\circ}\right)\)

7. \(\sin \left(60^{\circ}\right)=2 \sin \left(30^{\circ}\right) \cos \left(30^{\circ}\right)\)

8. \(\cos \left(60^{\circ}\right)=\cos^2 \left(30^{\circ}\right)-\sin^2 \left(30^{\circ}\right)\)

9. \(\tan \left(60^{\circ}\right)=\dfrac{2 \tan \left(30^{\circ}\right)}{1-\tan^2 \left(30^{\circ}\right)}\)

For Problems 10 and 11, determine if the statement is true or false. Explain your answer.

10. If \(\cos \left(\alpha\right)=0.32\), then \(\cos \left(2 \alpha\right)=0.64\).

11. If \(\sin\left( \phi\right)=r\), then \(\sin \left(2 \phi\right)=2 r\).

For Problems 12 - 31, use the Double Angle Identities to simplify the expression. Leave your answer in exact form.

12. \(2 \sin \left(34^{\circ}\right) \cos \left(34^{\circ}\right)\)

13. \(\cos^2\left( \dfrac{\pi}{10}\right)-\sin^2 \left(\dfrac{\pi}{10}\right)\)

14. \(1-2 \sin^2 \left(\dfrac{\pi}{16}\right)\)

15. \(2 \cos^2 \left(18^{\circ}\right)-1\)

16. \(\cos^2 \left(3 \theta\right)-\sin^2 \left(3 \theta\right)\)

17. \(2 \sin \left(2 \alpha\right) \cos \left(2 \alpha\right)\)

18. \(2 \sin \left(5 t\right) \cos \left(5 t\right)\)

19. \(\cos^2 \left(4 w\right)-\sin^2 \left(4 w\right)\)

20. \(\dfrac{2 \tan \left(64^{\circ}\right)}{1-\tan^2\left( 64^{\circ}\right)}\)

21. \(\dfrac{2 \tan \left(\frac{\pi}{5}\right)}{1-\tan^2 \left(\frac{\pi}{5}\right)}\)

22. \(2 \cos^2 \left(2 \beta\right)-1\)

23. \(1-2 \sin^2 \left(6 s\right)\)

24. \(\cos ^{2}\left(28^{\circ}\right)-\sin^{2}\left(28^{\circ}\right)\)

25. \(2\cos^{2} \left(37^{\circ} \right)-1\)

26. \(1-2\sin^{2}\left(17^{\circ}\right)\)

27. \(\cos^{2}\left(37^{\circ} \right)-\sin ^{2}\left(37^{\circ}\right)\)

28. \(\cos^{2} \left(9x\right)-\sin^{2} \left(9x\right)\)

29. \(\cos ^{2} \left(6x\right)-\sin ^{2} \left(6x\right)\)

30. \(4\sin \left(8x\right) \cos\left(8x\right)\)

31. \(6\sin \left(5x\right) \cos\left(5x\right)\)

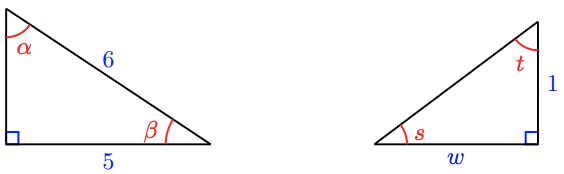
For Problems 32 - 35, use the figures to find the trigonometric ratios.

32.  

    1. \(\sin \left(\alpha\right)\)

    2. \(\cos \left(\alpha\right)\)

    3. \(\tan \left(\alpha\right)\)

    4. \(\sin \left(2\alpha\right)\)

    5. \(\cos \left(2\alpha\right)\)

    6. \(\tan \left(2\alpha\right)\)

33.  

    1. \(\sin \left(\beta\right)\)

    2. \(\cos \left(\beta\right)\)

    3. \(\tan \left(\beta\right)\)

    4. \(\sin \left(2\beta\right)\)

    5. \(\cos \left(2\beta\right)\)

    6. \(\tan \left(2\beta\right)\)

34.  

    1. \(\sin \left(s\right)\)

    2. \(\cos \left(s\right)\)

    3. \(\tan \left(s\right)\)

    4. \(\sin \left(2s\right)\)

    5. \(\cos \left(2s\right)\)

    6. \(\tan \left(2s\right)\)

35.  

    1. \(\sin \left(t\right)\)

    2. \(\cos \left(t\right)\)

    3. \(\tan \left(t\right)\)

    4. \(\sin \left(2t\right)\)

    5. \(\cos \left(2t\right)\)

    6. \(\tan \left(2t\right)\)

36. Suppose \(\cos \left(\theta\right)=\frac{12}{13}\) and \(\frac{3 \pi}{2}<\theta<2 \pi\). Compute exact values for the following.

    1. \(\sin \left(\theta\right)\)

    2. \(\sin \left(2 \theta\right)\)

    3. \(\cos \left(2 \theta\right)\)

    4. \(\tan \left(2 \theta\right)\)

    5. Sketch the angles \(\theta\) and \(2 \theta\).

37. Suppose \(\sin \left(\phi\right)=\frac{5}{6}\) and \(\frac{\pi}{2}<\phi<\pi\). Compute exact values for the following.

    1. \(\cos \left(\phi\right)\)

    2. \(\sin \left(2 \phi\right)\)

    3. \(\cos \left(2 \phi\right)\)

    4. \(\tan \left(2 \phi\right)\)

    5. Sketch the angles \(\phi\) and \(2 \phi\).

38. If \(\tan \left(u\right)=-4\) and \(270^{\circ}<u<360^{\circ}\), find exact values for the following.

    1. \(\tan \left(2 u\right)\)

    2. \(\cos \left(2 u\right)\)

    3. \(\sin \left(2 u\right)\)

39. If \(\tan \left(v\right)=\frac{2}{3}\) and \(180^{\circ}<v<270^{\circ}\), find exact values for the following.

    1. \(\tan \left(2v\right)\)

    2. \(\cos \left(2v\right)\)

    3. \(\sin \left(2v\right)\)

For Problems 40 - 49, use the given information about \(\theta\) to find the exact values of \(\sin(2\theta)\), \(\cos(2\theta)\), and \(\tan(2\theta)\)

40. \(\sin(\theta) = -\dfrac{7}{25}\) where \(\dfrac{3\pi}{2} < \theta < 2\pi\)

41. \(\cos(\theta) = \dfrac{28}{53}\) where \(0 < \theta < \dfrac{\pi}{2}\)

42. \(\tan(\theta) = \dfrac{12}{5}\) where \(\pi < \theta < \dfrac{3\pi}{2}\)

43. \(\csc(\theta) = 4\) where \(\dfrac{\pi}{2} < \theta < \pi\)

44. \(\cos(\theta) = \dfrac{3}{5}\) where \(0 < \theta < \dfrac{\pi}{2}\)

45. \(\sin(\theta) = -\dfrac{4}{5}\) where \(\pi < \theta < \dfrac{3\pi}{2}\)

46. \(\cos(\theta) = \dfrac{12}{13}\) where \(\dfrac{3\pi}{2} < \theta < 2\pi\)

47. \(\sin(\theta) = \dfrac{5}{13}\) where \(\dfrac{\pi}{2} < \theta < \pi\)

48. \(\sec(\theta) = \sqrt{5}\) where \(\dfrac{3\pi}{2} < \theta < 2\pi\)

49. \(\tan(\theta) = -2\) where \(\dfrac{\pi}{2} < \theta < \pi\)

50. Suppose \(\theta\) is a Quadrant I angle with \(\sin(\theta) = x\). Verify the following formulas

    1. \(\cos(\theta) = \sqrt{1-x^2}\)

    2. \(\sin(2\theta) = 2x\sqrt{1-x^2}\)

    3. \(\cos(2\theta) = 1 - 2x^2\)

51. Suppose \(\theta\) is a Quadrant I angle with \(\tan(\theta) = x\). Verify the following formulas

    1. \(\cos(\theta) = \dfrac{1}{\sqrt{x^2+1}}\)

    2. \(\sin(\theta) = \dfrac{x}{\sqrt{x^2+1}}\)

    3. \(\sin(2\theta) = \dfrac{2x}{x^2+1}\)

    4. \(\cos(2\theta) = \dfrac{1-x^2}{x^2+1}\)

52. If \(\sin(\theta) = \dfrac{x}{2}\) for \(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), find an expression for \(\cos(2\theta)\) in terms of \(x\).

53. If \(\tan(\theta) = \dfrac{x}{7}\) for \(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), find an expression for \(\sin(2\theta)\) in terms of \(x\).

For Problems 54 - 58, graph one cycle of the given function by hand.

54. \( f(x) = 4\sin\left( 3x \right)\cos\left( 3x \right) \)

55. \( g(x) = \dfrac{2}{3}\cos^2\left( \frac{\pi}{3} x \right) - \dfrac{1}{2} \)

56. \( h(x) = -\dfrac{5}{7} \sin\left( \frac{1}{3}x \right) \cos\left( \frac{1}{3} x \right) \)

57. \( k(x) = \dfrac{3 \tan\left( \frac{1}{2}x \right)}{2 - 2\tan^2\left( \frac{1}{2}x \right)} \)

58. \( m(x) = 2\cos^2\left( 5x \right) - 2\sin^2\left( 5x \right) \)

Proofs

For Problems 59 - 63, prove the given identity for any right triangle \( \triangle ABC \), where \( C \) is a right angle.

59. \(\sin\left(A-B\right) = \cos\left(2B\right)\)

60. \(\cos\left(A-B\right) = \sin\left(2A\right)\)

61. \(\sin\left(2A\right) = \dfrac{2ab}{c^2}\)

62. \(\cos\left(2A\right) = \dfrac{b^2 - a^2}{c^2}\)

63. \(\tan\left(2A\right) = \dfrac{2ab}{b^2 - a^2}\)

64. Prove the Double-Angle Identity \(\sin \left(2 \theta\right)=2 \sin\left( \theta\right) \cos \left(\theta\right)\).

65. Prove the Double-Angle Identity \(\cos \left(2 \theta\right)=\cos^2 \left(\theta\right)-\sin^2 \left(\theta\right)\).

For Problems 66 and 67,
(a) Use graphs to decide if the equation is an identity.
(b) If the equation is not an identity, find a value of the variable that makes the equation false.

66. \(\cos \left(4 \theta\right)=4 \cos \left(\theta\right)\)

67. \(\cos \left(2 x\right)=\left(\cos \left(x\right)+\sin \left(x\right)\right)\left(\cos\left( x\right)-\sin \left(x\right)\right)\)

For Problems 68 - 94, prove the identity. Assume all quantities are defined.

68. \((\cos(\theta) + \sin(\theta))^2 = 1 + \sin(2\theta)\)

69. \((\cos(\theta) - \sin(\theta))^2 = 1 - \sin(2\theta)\)

70. \( \dfrac{\sin\left( 2\theta \right)}{\sin\left( \theta \right)} - \dfrac{\cos\left( 2\theta \right)}{\cos\left( \theta \right)} = \sec\left( \theta \right) \)

71. \( \dfrac{\sin\left( 3\theta \right)}{\sin\left( \theta \right)} - \dfrac{\cos\left( 3\theta \right)}{\cos\left( \theta \right)} = 2 \)

72. \(\tan(2\theta) = \dfrac{1}{1-\tan(\theta)} - \dfrac{1}{1+\tan(\theta)}\)

73. \(\csc(2\theta) = \dfrac{\cot(\theta) + \tan(\theta)}{2}\)

74. \(\left(\sin ^{2} x-1\right)^{2} =\cos \left(2x\right)+\sin ^{4} x\)

75. \(\sin \left(2x\right)=\dfrac{2\tan \left(x\right)}{1+\tan ^{2} \left(x\right)}\)

76. \(\tan \left(2x\right)=\dfrac{2\sin \left(x\right)\cos \left(x\right)}{2\cos ^{2} \left(x\right)-1}\)

77. \(\cot \left(x\right)-\tan \left(x\right)=2\cot \left(2x\right)\)

78. \(\dfrac{\sin \left(2\theta \right)}{1+\cos \left(2\theta \right)} =\tan \left(\theta \right)\)

79. \(\cos \left(2\alpha \right)=\dfrac{1-\tan ^{2} \left(\alpha \right)}{1+\tan ^{2} \left(\alpha \right)}\)

80. \(\dfrac{1+\cos \left(2t\right)}{\sin \left(2t\right)-\cos \left(t\right)} =\dfrac{2\cos \left(t\right)}{2\sin \left(t\right)-1}\)

81. \(\sin \left(3x\right)=3\sin \left(x\right)\cos ^{2} \left(x\right)-\sin ^{3} (x)\)

82. \(\cos \left(3x\right)=\cos ^{3} (x)-3\sin ^{2} (x)\cos \left(x\right)\)

83. \(8 \sin^{4}(\theta) = \cos(4\theta) - 4\cos(2\theta)+3\)

84. \(8 \cos^{4}(\theta) = \cos(4\theta) + 4\cos(2\theta)+3\)

85. \(\sin(3\theta) = 3\sin(\theta) - 4\sin^{3}(\theta)\)

86. \(\sin(4\theta) = 4\sin(\theta)\cos^{3}(\theta) - 4\sin^{3}(\theta)\cos(\theta)\)

87. \(32\sin^{2}(\theta) \cos^{4}(\theta) = 2 + \cos(2\theta) - 2\cos(4\theta) - \cos(6\theta)\)

88. \(32\sin^{4}(\theta) \cos^{2}(\theta) = 2 - \cos(2\theta) - 2\cos(4\theta) + \cos(6\theta)\)

89. \(\cos(4\theta) = 8\cos^{4}(\theta) - 8\cos^{2}(\theta) + 1\)

90. \(\cos(8\theta) = 128\cos^{8}(\theta)-256\cos^{6}(\theta)+160\cos^{4}(\theta)-32\cos^{2}(\theta)+1\)

91. \(\sec(2\theta) = \dfrac{\cos(\theta)}{\cos(\theta) + \sin(\theta)} + \dfrac{\sin(\theta)}{\cos(\theta)-\sin(\theta)}\)

92. \(\dfrac{1}{\cos(\theta) - \sin(\theta)} + \dfrac{1}{\cos(\theta) + \sin(\theta)} = \dfrac{2\cos(\theta)}{\cos(2\theta)}\)

93. \(\dfrac{1}{\cos(\theta) - \sin(\theta)} - \dfrac{1}{\cos(\theta) + \sin(\theta)} = \dfrac{2\sin(\theta)}{\cos(2\theta)}\)

94. \( \dfrac{\cos^2\left( \psi \right)}{\cos^2\left( \theta \right)} = \dfrac{1 + \cos\left( 2 \psi \right)}{1 + \cos\left( 2 \theta \right)} \)

Challenge Problems

95. Some trigonometry textbooks used to claim (incorrectly) that \(\sin\left(\theta\right) + \cos\left(\theta\right) = \sqrt{1 + \sin\left(2\theta\right)} \) was an identity. Give an example of a specific angle \(\theta \) that would make that equation false. Is \(\sin\left(\theta\right) + \cos\left(\theta\right) = \pm\sqrt{1 + \sin\left(2\theta\right)} \) an identity? Justify your answer.

96. In general, what is the largest value that \(\sin\left(\theta\right)\cos\left(\theta\right) \) can take? Justify your answer.