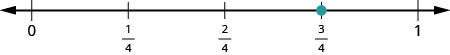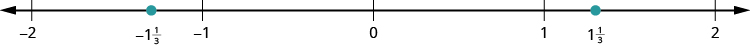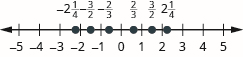Model Equivalent Fractions
Let’s think about Andy and Bobby and their favorite food again. If Andy eats \(\dfrac{1}{2}\) of a pizza and Bobby eats \(\dfrac{2}{4}\) of the pizza, have they eaten the same amount of pizza? In other words, does \(\dfrac{1}{2} = \dfrac{2}{4}\)? We can use fraction tiles to find out whether Andy and Bobby have eaten equivalent parts of the pizza.
Definition: Equivalent Fractions
Equivalent fractions are fractions that have the same value.
Fraction tiles serve as a useful model of equivalent fractions. You may want to use fraction tiles to do the following activity. Or you might make a copy of Figure 4.3 and extend it to include eighths, tenths, and twelfths.
Start with a \(\dfrac{1}{2}\) tile. How many fourths equal one-half? How many of the \(\dfrac{1}{4}\) tiles exactly cover the \(\dfrac{1}{2}\) tile?
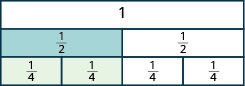
Figure \(\PageIndex{7}\)
Since two \(\dfrac{1}{4}\) tiles cover the \(\dfrac{1}{2}\) tile, we see that \(\dfrac{2}{4}\) is the same as \(\dfrac{1}{2}\), or \(\dfrac{2}{4} = \dfrac{1}{2}\).
How many of the \(\dfrac{1}{6}\) tiles cover the \(\dfrac{1}{2}\) tile?
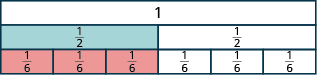
Figure \(\PageIndex{8}\)
Since three \(\dfrac{1}{6}\) tiles cover the \(\dfrac{1}{2}\) tile, we see that \(\dfrac{3}{6}\) is the same as \(\dfrac{1}{2}\). So, \(\dfrac{3}{6} = \dfrac{1}{2}\). The fractions are equivalent fractions.
Example \(\PageIndex{13}\): equivalent fractions
Use fraction tiles to find equivalent fractions. Show your result with a figure.
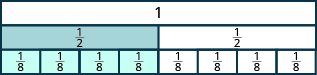
- How many eighths equal one-half?
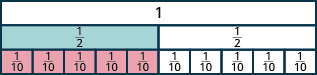
- How many tenths equal one-half?
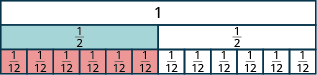
- How many twelfths equal one-half?
Solution
- It takes four \(\dfrac{1}{8}\) tiles to exactly cover the \(\dfrac{1}{2}\) tile, so \(\dfrac{4}{8} = \dfrac{1}{2}\).
- It takes five \(\dfrac{1}{10}\) tiles to exactly cover the \(\dfrac{1}{2}\) tile, so \(\dfrac{5}{10} = \dfrac{1}{2}\).
- It takes six \(\dfrac{1}{12}\) tiles to exactly cover the \(\dfrac{1}{2}\) tile, so \(\dfrac{6}{12} = \dfrac{1}{2}\).
Suppose you had tiles marked \(\dfrac{1}{20}\). How many of them would it take to equal \(\dfrac{1}{2}\)? Are you thinking ten tiles? If you are, you’re right, because \(\dfrac{10}{20} = \dfrac{1}{2}\).
We have shown that \(\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}, \dfrac{4}{8}, \dfrac{5}{10}, \dfrac{6}{12}\), and \(\dfrac{10}{20}\) are all equivalent fractions.
Exercise \(\PageIndex{25}\)
Use fraction tiles to find equivalent fractions: How many eighths equal one-fourth?
- Answer
-
\(2\)
Exercise \(\PageIndex{26}\)
Use fraction tiles to find equivalent fractions: How many twelfths equal one-fourth?
- Answer
-
\(3\)
Find Equivalent Fractions
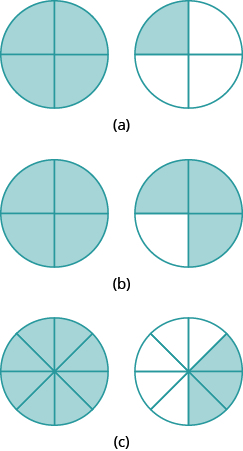
We used fraction tiles to show that there are many fractions equivalent to \(\dfrac{1}{2}\). For example, \(\dfrac{2}{4}, \dfrac{3}{6}\), and \(\dfrac{4}{8}\) are all equivalent to \(\dfrac{1}{2}\). When we lined up the fraction tiles, it took four of the \(\dfrac{1}{8}\) tiles to make the same length as a \(\dfrac{1}{2}\) tile. This showed that \(\dfrac{4}{8} = \dfrac{1}{2}\). See Example \(\PageIndex{13}\).
We can show this with pizzas, too. Figure \(\PageIndex{9a}\) shows a single pizza, cut into two equal pieces with \(\dfrac{1}{2}\) shaded. Figure \(\PageIndex{9b}\) shows a second pizza of the same size, cut into eight pieces with \(\dfrac{4}{8}\) shaded.
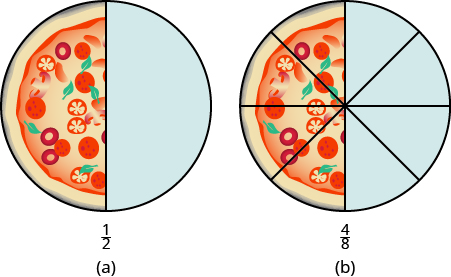
Figure \(\PageIndex{9}\)
This is another way to show that \(\dfrac{1}{2}\) is equivalent to \(\dfrac{4}{8}\). How can we use mathematics to change \(\dfrac{1}{2}\) into \(frac{4}{8}\)? How could you take a pizza that is cut into two pieces and cut it into eight pieces? You could cut each of the two larger pieces into four smaller pieces! The whole pizza would then be cut into eight pieces instead of just two. Mathematically, what we’ve described could be written as:
\[\dfrac{1 \cdot \textcolor{blue}{4}}{2 \cdot \textcolor{blue}{4}} = \dfrac{4}{8} \nonumber \]
These models lead to the Equivalent Fractions Property, which states that if we multiply the numerator and denominator of a fraction by the same number, the value of the fraction does not change.
Definition: Equivalent Fractions Property
If \(a\), \(b\), and \(c\) are numbers where \(b ≠ 0\) and \(c ≠ 0\), then
\[\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c}\]
When working with fractions, it is often necessary to express the same fraction in different forms. To find equivalent forms of a fraction, we can use the Equivalent Fractions Property. For example, consider the fraction one-half.
\[\begin{split} \dfrac{1 \cdot \textcolor{blue}{3}}{2 \cdot \textcolor{blue}{3}} = \dfrac{3}{6} \; & so \; \dfrac{1}{2} = \dfrac{3}{6} \\ \dfrac{1 \cdot \textcolor{blue}{2}}{2 \cdot \textcolor{blue}{2}} = \dfrac{2}{4} \; & so \; \dfrac{1}{2} = \dfrac{2}{4} \\ \dfrac{1 \cdot \textcolor{blue}{10}}{2 \cdot \textcolor{blue}{10}} = \dfrac{10}{20} \; & so \; \dfrac{1}{2} = \dfrac{10}{20} \end{split} \nonumber \]
So, we say that \(\dfrac{1}{2}, \dfrac{2}{4}, \dfrac{3}{6}\), and \(\dfrac{10}{20}\) are equivalent fractions.
Example \(\PageIndex{14}\): equivalent fractions
Find three fractions equivalent to \(\dfrac{2}{5}\).
Solution
To find a fraction equivalent to \(\dfrac{2}{5}\), we multiply the numerator and denominator by the same number (but not zero). Let us multiply them by \(2\), \(3\), and \(5\).
\[\dfrac{2 \cdot \textcolor{blue}{2}}{5 \cdot \textcolor{blue}{2}} = \dfrac{4}{10} \qquad \dfrac{2 \cdot \textcolor{blue}{3}}{5 \cdot \textcolor{blue}{3}} = \dfrac{6}{15} \qquad \dfrac{2 \cdot \textcolor{blue}{5}}{5 \cdot \textcolor{blue}{5}} = \dfrac{10}{25} \nonumber \]
So, \(\dfrac{4}{10}, \dfrac{6}{15}\), and \(\dfrac{10}{25}\) are equivalent to \(\dfrac{2}{5}\).
Exercise \(\PageIndex{27}\)
Find three fractions equivalent to \(\dfrac{3}{5}\).
- Answer
-
Correct answers include \(\dfrac{6}{10}, \dfrac{9}{15}\) and \(\dfrac{12}{20}\)
Exercise \(\PageIndex{28}\)
Find three fractions equivalent to \(\dfrac{4}{5}\).
- Answer
-
Correct answers include \(\dfrac{8}{10}, \dfrac{12}{15}\) and \(\dfrac{16}{20}\)
Example \(\PageIndex{15}\): equivalent fractions
Find a fraction with a denominator of 21 that is equivalent to \(\dfrac{2}{7}\).
Solution
To find equivalent fractions, we multiply the numerator and denominator by the same number. In this case, we need to multiply the denominator by a number that will result in \(21\).
Since we can multiply \(7\) by \(3\) to get \(21\), we can find the equivalent fraction by multiplying both the numerator and denominator by \(3\).
\[\dfrac{2}{7} = \dfrac{2 \cdot \textcolor{blue}{3}}{7 \cdot \textcolor{blue}{3}} = \dfrac{6}{21} \nonumber \]
Exercise \(\PageIndex{29}\)
Find a fraction with a denominator of \(21\) that is equivalent to \(\dfrac{6}{7}\).
- Answer
-
\(\dfrac{18}{21}\)
Exercise \(\PageIndex{30}\)
Find a fraction with a denominator of \(100\) that is equivalent to \(\dfrac{3}{10}\).
- Answer
-
\(\dfrac{30}{100}\)
Locate Fractions and Mixed Numbers on the Number Line
Now we are ready to plot fractions on a number line. This will help us visualize fractions and understand their values.
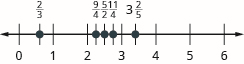
Let us locate \(\dfrac{1}{5}, \dfrac{4}{5}, 3, 3 \dfrac{1}{3}, \dfrac{7}{4}, \dfrac{9}{2}, 5\), and \(\dfrac{8}{3}\) on the number line. We will start with the whole numbers \(3\) and \(5\) because they are the easiest to plot.

The proper fractions listed are \(\dfrac{1}{5}\) and \(\dfrac{4}{5}\). We know proper fractions have values less than one, so \(\dfrac{1}{5}\) and \(\dfrac{1}{5}\) are located between the whole numbers \(0\) and \(1\). The denominators are both \(5\), so we need to divide the segment of the number line between \(0\) and \(1\) into five equal parts. We can do this by drawing four equally spaced marks on the number line, which we can then label as \(\dfrac{1}{5}, \dfrac{2}{5}, \dfrac{3}{5}\), and \(\dfrac{4}{5}\). Now plot points at \(\dfrac{1}{5}\) and \(\dfrac{4}{5}\).

The only mixed number to plot is \(3 \dfrac{1}{3}\). Between what two whole numbers is \(3 \dfrac{1}{3}\)? Remember that a mixed number is a whole number plus a proper fraction, so \(3 \dfrac{1}{3} > 3\). Since it is greater than \(3\), but not a whole unit greater, \(3 \dfrac{1}{3}\) is between \(3\) and \(4\). We need to divide the portion of the number line between \(3\) and \(4\) into three equal pieces (thirds) and plot \(3 \dfrac{1}{3}\) at the first mark.

Finally, look at the improper fractions \(\dfrac{7}{4}, \dfrac{9}{2}\), and \(\dfrac{8}{3}\). Locating these points will be easier if you change each of them to a mixed number.
\[\dfrac{7}{4} = 1 \dfrac{3}{4}, \qquad \dfrac{9}{2} = 4 \dfrac{1}{2}, \qquad \dfrac{8}{3} = 2 \dfrac{2}{3} \nonumber \]
Here is the number line with all the points plotted.

Example \(\PageIndex{16}\): locate and label
Locate and label the following on a number line: \(\dfrac{3}{4}, \dfrac{4}{3}, \dfrac{5}{3}, 4 \dfrac{1}{5}\), and \(\dfrac{7}{2}\).
Solution
Start by locating the proper fraction \(\dfrac{3}{4}\). It is between \(0\) and \(1\). To do this, divide the distance between \(0\) and \(1\) into four equal parts. Then plot \(\dfrac{3}{4}\).
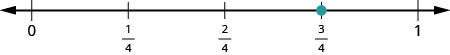
Next, locate the mixed number \(4 \dfrac{1}{5}\). It is between \(4\) and \(5\) on the number line. Divide the number line between \(4\) and \(5\) into five equal parts, and then plot \(4 \dfrac{1}{5}\) one-fifth of the way between \(4\) and \(5\).

Now locate the improper fractions \(\dfrac{4}{3}\) and \(\dfrac{5}{3}\). It is easier to plot them if we convert them to mixed numbers first.
\[\dfrac{4}{3} = 1 \dfrac{1}{3}, \qquad \dfrac{5}{3} = 1 \dfrac{2}{3} \nonumber\]
Divide the distance between \(1\) and \(2\) into thirds.

Next let us plot \(\dfrac{7}{2}\). We write it as a mixed number, \(\dfrac{7}{2} = 3 \dfrac{1}{2}\). Plot it between \(3\) and \(4\).
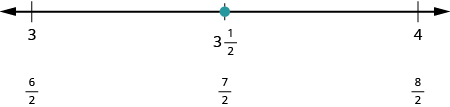
The number line shows all the numbers located on the number line.

Exercise \(\PageIndex{31}\)
Locate and label the following on a number line: \(\dfrac{1}{3}, \dfrac{5}{4}, \dfrac{7}{4}, 2 \dfrac{3}{5}, \dfrac{9}{2}\).
- Answer
-
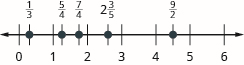
Exercise \(\PageIndex{32}\)
Locate and label the following on a number line: \(\dfrac{2}{3}, \dfrac{5}{2}, \dfrac{9}{4}, \dfrac{11}{4}, 3 \dfrac{2}{5}\).
- Answer
-
In Introduction to Integers, we defined the opposite of a number. It is the number that is the same distance from zero on the number line but on the opposite side of zero. We saw, for example, that the opposite of \(7\) is \(−7\) and the opposite of \(−\)7 is \(7\).

Fractions have opposites, too. The opposite of \(\dfrac{3}{4}\) is \(− \dfrac{3}{4}\). It is the same distance from \(0\) on the number line, but on the opposite side of \(0\).
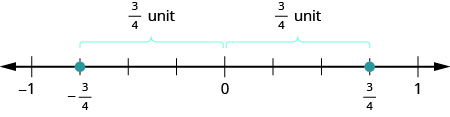
Thinking of negative fractions as the opposite of positive fractions will help us locate them on the number line. To locate \(− \dfrac{15}{8}\) on the number line, first think of where \(\dfrac{15}{8}\) is located. It is an improper fraction, so we first convert it to the mixed number \(1 \dfrac{7}{8}\) and see that it will be between \(1\) and \(2\) on the number line. So its opposite, \(− \dfrac{15}{8}\), will be between \(−1\) and \(−2\) on the number line.

Example \(\PageIndex{17}\): locate and label
Locate and label the following on the number line: \(\dfrac{1}{4}, − \dfrac{1}{4}, 1 \dfrac{1}{3}, −1 \dfrac{1}{3}, \dfrac{5}{2}\), and \(− \dfrac{5}{2}\).
Solution
Draw a number line. Mark \(0\) in the middle and then mark several units to the left and right.
To locate \(\dfrac{1}{4}\), divide the interval between \(0\) and \(1\) into four equal parts. Each part represents one-quarter of the distance. So plot \(\dfrac{1}{4}\) at the first mark.

To locate \(− \dfrac{1}{4}\), divide the interval between \(0\) and \(−1\) into four equal parts. Plot \(− \dfrac{1}{4}\) at the first mark to the left of \(0\).

Since \(1 \dfrac{1}{3}\) is between \(1\) and \(2\), divide the interval between \(1\) and \(2\) into three equal parts. Plot \(1 \dfrac{1}{3}\) at the first mark to the right of \(1\). Then since \(−1 \dfrac{1}{3}\) is the opposite of \(1 \dfrac{1}{3}\) it is between \(−1\) and \(−2\). Divide the interval between \(−1\) and \(−2\) into three equal parts. Plot \(−1 \dfrac{1}{3}\) at the first mark to the left of \(−1\).
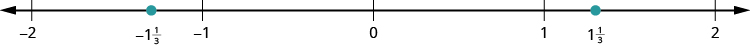
To locate \(\dfrac{5}{2}\) and \(− \dfrac{5}{2}\), it may be helpful to rewrite them as the mixed numbers \(2 \dfrac{1}{2}\) and \(−2 \dfrac{1}{2}\). Since \(2 \dfrac{1}{2}\) is between \(2\) and \(3\), divide the interval between \(2\) and \(3\) into two equal parts. Plot \(\dfrac{5}{2}\) at the mark. Then since \(−2 \dfrac{1}{2}\) is between \(−2\) and \(−3\), divide the interval between \(−2\) and \(−3\) into two equal parts. Plot \(− \dfrac{5}{2}\) at the mark.

Exercise \(\PageIndex{33}\)
Locate and label each of the given fractions on a number line: \(\dfrac{2}{3}, − \dfrac{2}{3}, 2 \dfrac{1}{4}, −2 \dfrac{1}{4}, \dfrac{3}{2}, − \dfrac{3}{2}\)
- Answer
-
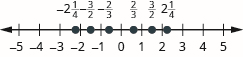
Exercise \(\PageIndex{34}\)
Locate and label each of the given fractions on a number line: \(\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{1}{2}, −1 \dfrac{1}{2}, \dfrac{7}{3}, − \dfrac{7}{3}\)
- Answer
-
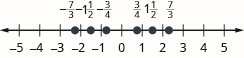
Order Fractions and Mixed Numbers
We can use the inequality symbols to order fractions. Remember that \(a > b\) means that \(a\) is to the right of \(b\) on the number line. As we move from left to right on a number line, the values increase.
Example \(\PageIndex{18}\): order
Order each of the following pairs of numbers, using \(<\) or \(>\):
- \(− \dfrac{2}{3}\)____\(−1\)
- \(−3 \dfrac{1}{2}\)____\(−3\)
- \(− \dfrac{3}{7}\)____\(− \dfrac{3}{8}\)
- \(−2\)____\(− \dfrac{16}{9}\)
Solution
- \(− \dfrac{2}{3} > −1\)

- \(−3 \dfrac{1}{2} < −3\)

- \(− \dfrac{3}{7} < − \dfrac{3}{8}\)

- \(−2 < − \dfrac{16}{9}\)

Exercise \(\PageIndex{35}\)
Order each of the following pairs of numbers, using \(<\) or \(>\):
- \(− \dfrac{1}{3}\)__\(−1\)
- \(−1 \dfrac{1}{2}\)__\(− 2\)
- \(− \dfrac{2}{3}\)__\(− \dfrac{1}{3}\)
- \(−3\)__\(− \dfrac{7}{3}\)
- Answer a
-
\(>\)
- Answer b
-
\(>\)
- Answer c
-
\(<\)
- Answer d
-
\(<\)
Exercise \(\PageIndex{36}\)
Order each of the following pairs of numbers, using \(<\) or \(>\):
- \(−3\)__\(− \dfrac{17}{5}\)
- \(−2 \dfrac{1}{4}\)__\(−2\)
- \(− \dfrac{3}{5}\)__\(− \dfrac{4}{5}\)
- \(−4\)__\(− \dfrac{10}{3}\)
- Answer a
-
\(>\)
- Answer b
-
\(<\)
- Answer c
-
\(>\)
- Answer d
-
\(<\)
Access Additional Online Resources
- Introduction to Fractions
- Identify Fractions Using Pattern Blocks
Key Concepts
- Property of One
- Any number, except zero, divided by itself is one.
\(\dfrac{a}{a}=1\), where \(a\neq 0\).
- Mixed Numbers
- A mixed number consists of a whole number \(a\) and a fraction \(\dfrac{b}{c}\) where \(c \neq 0\).
- It is written as follows: \(a\dfrac{b}{c}\) \(c \neq 0\)
- Proper and Improper Fractions
- The fraction \(\frac{a}{b}\) is a proper fraction if \(a<b\) and an improper fraction if \(a \geq b\).
- Convert an improper fraction to a mixed number.
- Divide the denominator into the numerator.
- Identify the quotient, remainder, and divisor.
- Write the mixed number as \(\dfrac{\text{remainder}}{\text{divisor}}\).
- Convert a mixed number to an improper fraction.
- Multiply the whole number by the denominator.
- Add the numerator to the product found in Step 1.
- Write the final sum over the original denominator.
- Equivalent Fractions Property
- If \(a\), \(b\) and \(c\) are numbers where \(b \neq 0\), \(c \neq 0\), then \(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]).
Glossary
- equivalent fractions
-
Equivalent fractions are two or more fractions that have the same value.
- fraction
-
A fraction is written \(\dfrac{a}{b}\). in a fraction, \(a\) is the numerator and \(b\) is the denominator. A fraction represents parts of a whole. The denominator \(b\) is the number of equal parts the whole has been divided into, and the numerator \(a\) indicates how many parts are included.
- mixed number
-
A mixed number consists of a whole number \(a\) and a fraction \(\dfrac{b}{c}\) where \(c \neq 0\). It is written as \(a\dfrac{b}{c}\), where \(c \neq 0\).
- proper and improper fractions
-
The fraction \(\dfrac{a}{b}\) is proper if \(a<b\) and improper if \(a>b\).
Practice Makes Perfect
In the following exercises, shade parts of circles or squares to model the following fractions.
- \(\dfrac{1}{2}\)
- \(\dfrac{1}{3}\)
- \(\dfrac{3}{4}\)
- \(\dfrac{2}{5}\)
- \(\dfrac{5}{6}\)
- \(\dfrac{7}{8}\)
- \(\dfrac{5}{8}\)
- \(\dfrac{7}{10}\)
In the following exercises, use fraction circles to make wholes, if possible, with the following pieces.
- 3 thirds
- 8 eighths
- 7 sixths
- 4 thirds
- 7 fifths
- 7 fourths
In the following exercises, name the improper fractions. Then write each improper fraction as a mixed number.
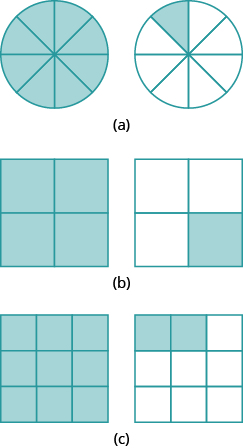
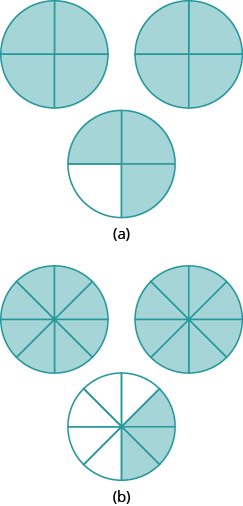
In the following exercises, draw fraction circles to model the given fraction.
- \(\dfrac{3}{3}\)
- \(\dfrac{4}{4}\)
- \(\dfrac{7}{4}\)
- \(\dfrac{5}{3}\)
- \(\dfrac{11}{6}\)
- \(\dfrac{13}{8}\)
- \(\dfrac{10}{3}\)
- \(\dfrac{9}{4}\)
In the following exercises, rewrite the improper fraction as a mixed number.
- \(\dfrac{3}{2}\)
- \(\dfrac{5}{3}\)
- \(\dfrac{11}{4}\)
- \(\dfrac{13}{5}\)
- \(\dfrac{25}{6}\)
- \(\dfrac{28}{9}\)
- \(\dfrac{42}{13}\)
- \(\dfrac{47}{15}\)
In the following exercises, rewrite the mixed number as an improper fraction.
- \(1 \dfrac{2}{3}\)
- \(1 \dfrac{2}{5}\)
- \(2 \dfrac{1}{4}\)
- \(2 \dfrac{5}{6}\)
- \(2 \dfrac{7}{9}\)
- \(2 \dfrac{5}{7}\)
- \(3 \dfrac{4}{7}\)
- \(3 \dfrac{5}{9}\)
In the following exercises, use fraction tiles or draw a figure to find equivalent fractions.
- How many sixths equal one-third?
- How many twelfths equal one-third?
- How many eighths equal three-fourths?
- How many twelfths equal three-fourths?
- How many fourths equal three-halves?
- How many sixths equal three-halves?
In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.
- \(\dfrac{1}{4}\)
- \(\dfrac{1}{3}\)
- \(\dfrac{3}{8}\)
- \(\dfrac{5}{6}\)
- \(\dfrac{2}{7}\)
- \(\dfrac{5}{9}\)
In the following exercises, plot the numbers on a number line.
- \(\dfrac{2}{3}, \dfrac{5}{4}, \dfrac{12}{5}\)
- \(\dfrac{1}{3}, \dfrac{7}{4}, \dfrac{13}{5}\)
- \(\dfrac{1}{4}, \dfrac{9}{5}, \dfrac{11}{3}\)
- \(\dfrac{7}{10}, \dfrac{5}{2}, \dfrac{13}{8}, 3\)
- \(2 \dfrac{1}{3}, −2 \dfrac{1}{3}\)
- \(1 \dfrac{3}{4}, −1 \dfrac{3}{5}\)
- \(\dfrac{3}{4}, − \dfrac{3}{4}, 1 \dfrac{2}{3}, −1 \dfrac{2}{3}, \dfrac{5}{2}, − \dfrac{5}{2}\)
- \(\dfrac{2}{5}, − \dfrac{2}{5}, 1 \dfrac{3}{4}, −1 \dfrac{3}{4}, \dfrac{8}{3}, − \dfrac{8}{3}\)
In the following exercises, order each of the following pairs of numbers, using < or >.
- −1__\(− \dfrac{1}{4}\)
- −1__\(− \dfrac{1}{3}\)
- \(−2 \dfrac{1}{2}\)__− 3
- \(−1 \dfrac{3}{4}\)__− 2
- \(− \dfrac{5}{12}\)__\(− \dfrac{7}{12}\)
- \(− \dfrac{9}{10}\)__\(− \dfrac{3}{10}\)
- −3__\(− \dfrac{13}{5}\)
- −4__\(− \dfrac{23}{6}\)
Everyday Math
- Music Measures A choreographed dance is broken into counts. A \(\dfrac{1}{1}\) count has one step in a count, a \(\dfrac{1}{2}\) count has two steps in a count and a 1 3 count has three steps in a count. How many steps would be in a \(\dfrac{1}{5}\) count? What type of count has four steps in it?
- Music Measures Fractions are used often in music. In 4 4 time, there are four quarter notes in one measure.
- How many measures would eight quarter notes make?
- The song “Happy Birthday to You” has 25 quarter notes. How many measures are there in “Happy Birthday to You?”
- Baking Nina is making five pans of fudge to serve after a music recital. For each pan, she needs 1 2 cup of walnuts.
- How many cups of walnuts does she need for five pans of fudge?
- Do you think it is easier to measure this amount when you use an improper fraction or a mixed number? Why?
Writing Exercises
- Give an example from your life experience (outside of school) where it was important to understand fractions.
- Explain how you locate the improper fraction \(\dfrac{21}{4}\) on a number line on which only the whole numbers from 0 through 10 are marked.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
Contributors and Attributions