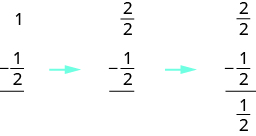Learning Objectives
- Model addition of mixed numbers with a common denominator
- Add mixed numbers with a common denominator
- Model subtraction of mixed numbers
- Subtract mixed numbers with a common denominator
- Add and subtract mixed numbers with different denominators
be prepared!
Before you get started, take this readiness quiz.
- Draw figure to model \(\dfrac{7}{3}\). If you missed this problem, review Example 4.1.6.
- Change \(\dfrac{11}{4}\) to a mixed number. If you missed this problem, review Example 4.1.9.
- Change \(3 \dfrac{1}{2}\) to an improper fraction. If you missed this problem, review Example 4.1.11.
Model Addition of Mixed Numbers with a Common Denominator
So far, we’ve added and subtracted proper and improper fractions, but not mixed numbers. Let’s begin by thinking about addition of mixed numbers using money.
If Ron has \(1\) dollar and \(1\) quarter, he has \(1 \dfrac{1}{4}\) dollars. If Don has \(2\) dollars and \(1\) quarter, he has \(2 \dfrac{1}{4}\) dollars. What if Ron and Don put their money together? They would have \(3\) dollars and \(2\) quarters. They add the dollars and add the quarters. This makes \(3 \dfrac{2}{4}\) dollars. Because two quarters is half a dollar, they would have \(3\) and a half dollars, or \(3 \dfrac{1}{2}\) dollars.
\[\begin{split} & 1 \dfrac{1}{4} \\ + & 2 \dfrac{1}{4} \\ \hline \\ & 3 \dfrac{2}{4} = 3 \dfrac{1}{2} \end{split} \nonumber \]
When you added the dollars and then added the quarters, you were adding the whole numbers and then adding the fractions.
\[1 \dfrac{1}{4} + 2 \dfrac{1}{4} \nonumber \]
We can use fraction circles to model this same example:
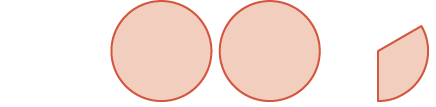
| Start with \(1 \dfrac{1}{4}\). |
one whole and one \(\dfrac{1}{4}\) pieces |
 |
\(1 \dfrac{1}{4}\) |
| Add \(2 \dfrac{1}{4}\) more. |
two wholes and one \(\dfrac{1}{4}\) pieces |
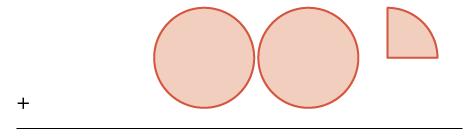 |
\(\begin{split}+ & 2 \dfrac{1}{4} \\ & \hline \end{split}\) |
| The sum is: |
three wholes and two \(\dfrac{1}{4}\)'s |
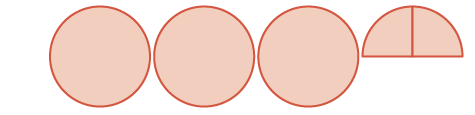 |
\(3 \dfrac{2}{4} = 3 \dfrac{1}{2}\) |
Example \(\PageIndex{1}\): model
Model \(2 \dfrac{1}{3} + 1 \dfrac{2}{3}\) and give the sum.
Solution
We will use fraction circles, whole circles for the whole numbers and \(\dfrac{1}{3}\) pieces for the fractions.
| two wholes and one \(\dfrac{1}{3}\) |
 |
\(2 \dfrac{1}{3}\) |
| plus one whole and two \(\dfrac{1}{3}\)s |
 |
\(\begin{split}+ & 1 \dfrac{2}{3} \\ & \hline \end{split}\) |
| sum is three wholes and three \(\dfrac{1}{3}\)s |
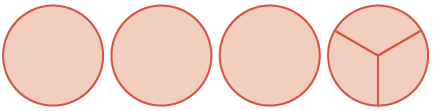 |
\(3 \dfrac{3}{3} = 4\) |
This is the same as \(4\) wholes. So, \(2 \dfrac{1}{3} + 1 \dfrac{2}{3} = 4\).
Exercise \(\PageIndex{1}\)
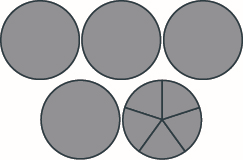
Use a model to add the following. Draw a picture to illustrate your model. \(1 \dfrac{2}{5} + 3 \dfrac{3}{5}\)
- Answer
-
\(5\)
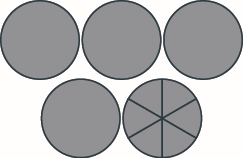
Exercise \(\PageIndex{2}\)
Use a model to add the following. Draw a picture to illustrate your model. \(2 \dfrac{1}{6} + 2 \dfrac{5}{6}\)
- Answer
-
\(5\)
Example \(\PageIndex{2}\): model
Model \(1 \dfrac{3}{5} + 2 \dfrac{3}{5}\) and give the sum as a mixed number.
Solution
We will use fraction circles, whole circles for the whole numbers and \(\dfrac{1}{5}\) pieces for the fractions.
| one whole and three \(\dfrac{1}{5}\)s |
 |
\(1 \dfrac{3}{5}\) |
| plus two wholes and three \(\dfrac{1}{5}\)s |
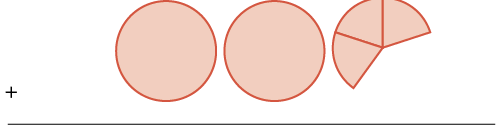 |
\(\begin{split}+ & 2 \dfrac{3}{5} \\ & \hline \end{split}\) |
| sum is three wholes and six \(\dfrac{1}{5}\)s |
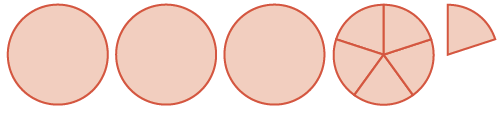 |
\(3 \dfrac{6}{5} = 4 \dfrac{1}{5}\) |
Adding the whole circles and fifth pieces, we got a sum of \(3 \dfrac{6}{5}\). We can see that \(\dfrac{6}{5}\) is equivalent to \(1 \dfrac{1}{5}\), so we add that to the \(3\) to get \(4 \dfrac{1}{5}\).
Exercise \(\PageIndex{3}\)
Model, and give the sum as a mixed number. Draw a picture to illustrate your model. \(2 \dfrac{5}{6} + 1 \dfrac{5}{6}\)
- Answer
-
\(4\dfrac{2}{3}\)
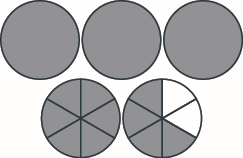
Exercise \(\PageIndex{4}\)
Model, and give the sum as a mixed number. Draw a picture to illustrate your model. \(1 \dfrac{5}{8} + 1 \dfrac{7}{8}\)
- Answer
-
\(3\dfrac{1}{2}\)
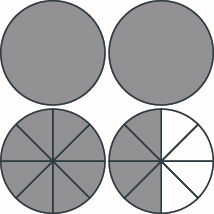
Add Mixed Numbers
Modeling with fraction circles helps illustrate the process for adding mixed numbers: We add the whole numbers and add the fractions, and then we simplify the result, if possible.
HOW TO: ADD MIXED NUMBERS WITH A COMMON DENOMINATOR
Step 1. Add the whole numbers.
Step 2. Add the fractions.
Step 3. Simplify, if possible.
Example \(\PageIndex{3}\): add
Add: \(3 \dfrac{4}{9} + 2 \dfrac{2}{9}\).
Solution
| Add the whole numbers. |
\(\begin{split} & \textcolor{red}{3} \dfrac{4}{9} \\ + & \textcolor{red}{2} \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5} \end{split}\) |
| Add the fractions. |
\(\begin{split} & 3 \textcolor{red}{\dfrac{4}{9}} \\ + & 2 \textcolor{red}{\dfrac{2}{9}} \\ \hline \\ & 5 \textcolor{red}{\dfrac{6}{9}} \end{split}\) |
| Simplify the fraction. |
\(\begin{split} & 3 \dfrac{4}{9} \\ + & 2 \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5 \dfrac{6}{9}} = 5 \dfrac{2}{3} \end{split}\) |
Exercise \(\PageIndex{5}\)
Find the sum: \(4 \dfrac{4}{7} + 1 \dfrac{2}{7}\).
- Answer
-
\(5\dfrac{6}{7}\)
Exercise \(\PageIndex{6}\)
Find the sum: \(2 \dfrac{3}{11} + 5 \dfrac{6}{11}\).
- Answer
-
\(7\dfrac{9}{11}\)
In Example \(\PageIndex{3}\), the sum of the fractions was a proper fraction. Now we will work through an example where the sum is an improper fraction.
Example \(\PageIndex{4}\): add
Find the sum: \(9 \dfrac{5}{9} + 5 \dfrac{7}{9}\).
Solution
| Add the whole numbers and then add the fractions. |
\(\begin{split} & 9 \dfrac{5}{9} \\ + & 5 \dfrac{7}{9} \\ \hline \\ & 14 \dfrac{12}{9} \end{split}\) |
| Rewrite \(\dfrac{12}{9}\) as an improper fraction. |
\(14 + 1 \dfrac{3}{9}\) |
| Add. |
\(15 \dfrac{3}{9}\) |
| Simplify. |
\(15 \dfrac{1}{3}\) |
Exercise \(\PageIndex{7}\)
Find the sum: \(8 \dfrac{7}{8} + 7 \dfrac{5}{8}\).
- Answer
-
\(16\dfrac{1}{2}\)
Exercise \(\PageIndex{8}\)
Find the sum: \(6 \dfrac{7}{9} + 8 \dfrac{5}{9}\).
- Answer
-
\(15\dfrac{1}{3}\)
An alternate method for adding mixed numbers is to convert the mixed numbers to improper fractions and then add the improper fractions. This method is usually written horizontally.
Example \(\PageIndex{5}\): add
Add by converting the mixed numbers to improper fractions: \(3 \dfrac{7}{8} + 4 \dfrac{3}{8}\).
Solution
| Convert to improper fractions. |
\(\dfrac{31}{8} + \dfrac{35}{8}\) |
| Add the fractions. |
\(\dfrac{31 + 35}{8}\) |
| Simplify the numerator. |
\(\dfrac{66}{8}\) |
| Rewrite as a mixed number. |
\(8 \dfrac{2}{8}\) |
| Simplify the fraction. |
\(8 \dfrac{1}{4}\) |
Since the problem was given in mixed number form, we will write the sum as a mixed number.
Exercise \(\PageIndex{9}\)
Find the sum by converting the mixed numbers to improper fractions: \(5 \dfrac{5}{9} + 3 \dfrac{7}{9}\)
- Answer
-
\(9\dfrac{1}{3}\)
Exercise \(\PageIndex{10}\)
Find the sum by converting the mixed numbers to improper fractions: \(3 \dfrac{7}{10} + 2 \dfrac{9}{10}\)
- Answer
-
\(6\dfrac{3}{5}\)
Table \(\PageIndex{1}\) compares the two methods of addition, using the expression \(3 \dfrac{2}{5} + 6 \dfrac{4}{5}\) as an example. Which way do you prefer?
Table \(\PageIndex{1}\)
| Mixed Numbers |
Improper Fractions |
| \(\begin{split} & 3 \dfrac{2}{5} \\ + & 6 \dfrac{4}{5} \\ \hline \\ & 9 \dfrac{6}{5} \end{split}\) |
\(3 \dfrac{2}{5} + 6 \dfrac{4}{5}\) |
| \(9 + \dfrac{6}{5}\) |
\(\dfrac{17}{5} + \dfrac{34}{5}\) |
| \(9 + 1 \dfrac{1}{5}\) |
\(\dfrac{51}{5}\) |
| \(10 \dfrac{1}{5}\) |
\(10 \dfrac{1}{5}\) |
Model Subtraction of Mixed Numbers
Let’s think of pizzas again to model subtraction of mixed numbers with a common denominator. Suppose you just baked a whole pizza and want to give your brother half of the pizza. What do you have to do to the pizza to give him half? You have to cut it into at least two pieces. Then you can give him half.
We will use fraction circles (pizzas!) to help us visualize the process. Start with one whole.

Figure \(\PageIndex{1}\)
Algebraically, you would write:
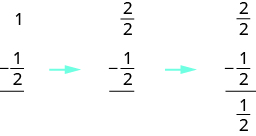
Example \(\PageIndex{6}\): subtract
Use a model to subtract: \(1 − \dfrac{1}{3}\).
Solution

Exercise \(\PageIndex{11}\)
Use a model to subtract: \(1 − \dfrac{1}{4}\).
- Answer
-
\(\dfrac{3}{4}\)
Exercise \(\PageIndex{12}\)
Use a model to subtract: \(1 − \dfrac{1}{5}\).
- Answer
-
\(\dfrac{4}{5}\)
What if we start with more than one whole? Let’s find out.
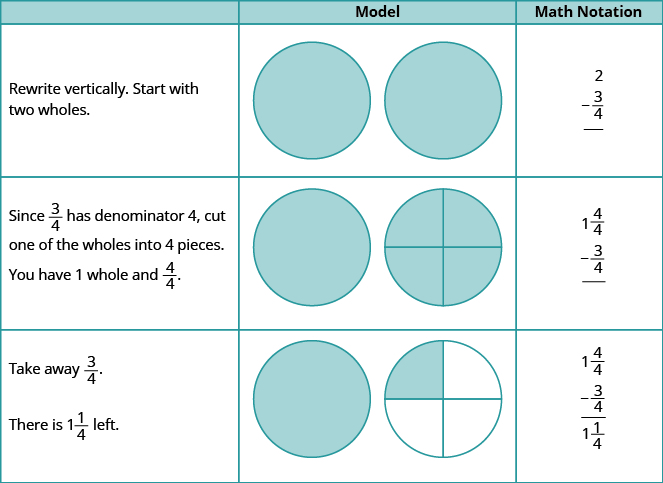
Example\(\PageIndex{7}\): subtract
Use a model to subtract: \(2 − \dfrac{3}{4}\).
Solution
Exercise \(\PageIndex{13}\)
Use a model to subtract: \(2 − \dfrac{1}{5}\).
- Answer
-
\(\dfrac{9}{5}\)
Exercise \(\PageIndex{14}\)
Use a model to subtract: \(2 − \dfrac{1}{3}\).
- Answer
-
\(\dfrac{5}{3}\)
In the next example, we’ll subtract more than one whole.
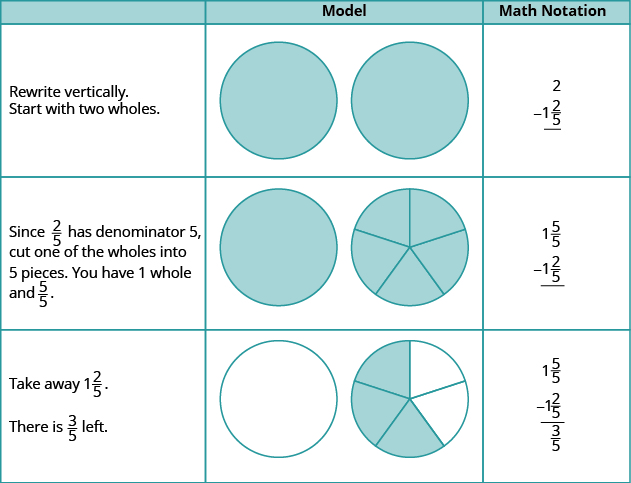
Example \(\PageIndex{8}\): subtract
Use a model to subtract: \(2 − 1 \dfrac{2}{5}\).
Solution
Exercise \(\PageIndex{15}\)
Use a model to subtract: \(2 − 1 \dfrac{1}{3}\).
- Answer
-
\(\dfrac{2}{3}\)
Exercise \(\PageIndex{16}\)
Use a model to subtract: \(2 − 1 \dfrac{1}{4}\).
- Answer
-
\(\dfrac{3}{4}\)
What if you start with a mixed number and need to subtract a fraction? Think about this situation: You need to put three quarters in a parking meter, but you have only a \(\$1\) bill and one quarter. What could you do? You could change the dollar bill into \(4\) quarters. The value of \(4\) quarters is the same as one dollar bill, but the \(4\) quarters are more useful for the parking meter. Now, instead of having a \(\$1\) bill and one quarter, you have \(5\) quarters and can put \(3\) quarters in the meter.
This models what happens when we subtract a fraction from a mixed number. We subtracted three quarters from one dollar and one quarter.
We can also model this using fraction circles, much like we did for addition of mixed numbers.
Example \(\PageIndex{9}\): subtract
Use a model to subtract: \(1 \dfrac{1}{4} − \dfrac{3}{4}\)
Solution
| Rewrite vertically. Start with one whole and one fourth. |
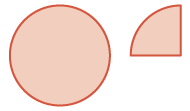 |
\(\begin{split} & \textcolor{red}{1 \dfrac{1}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}\) |
| Since the fractions have denominator 4, cut the whole into 4 pieces. You now have \(\dfrac{4}{4}\) and \(\dfrac{1}{4}\) which is \(\dfrac{5}{4}\). |
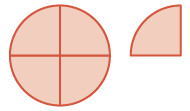 |
\(\begin{split} & \textcolor{red}{\dfrac{5}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}\) |
| Take away \(\dfrac{3}{4}\). There is \(\dfrac{1}{2}\) left. |
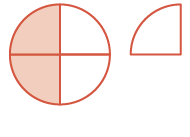 |
\(\begin{split} & \dfrac{5}{4}\\\textcolor{red}{- & \dfrac}3}{4}}\\ \hline \\ & \dfrac{2}{4} = \dfrac{1}{2} \end{split}\) |
Exercise \(\PageIndex{17}\)
Use a model to subtract. Draw a picture to illustrate your model. \(1 \dfrac{1}{3} − \dfrac{2}{3}\)
- Answer
-
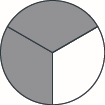
Exercise \(\PageIndex{18}\)
Use a model to subtract. Draw a picture to illustrate your model. \(1 \dfrac{1}{5} − \dfrac{4}{5}\)
- Answer
-
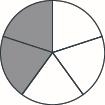
Contributors and Attributions