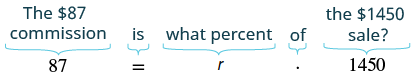6.3: Solve Sales Tax, Commission, and Discount Applications
- Last updated
- Save as PDF
- Page ID
- 21727
Learning Objectives
- Solve sales tax applications
- Solve commission applications
- Solve discount applications
- Solve mark-up applications
be prepared!
Before you get started, take this readiness quiz.
- Solve 0.0875(720) through multiplication. If you missed this problem, review Example 5.3.7.
- Solve 12.96 ÷ 0.04 through division. If you missed this problem, review Example 5.4.12.
Solve Sales Tax Applications
Sales tax and commissions are applications of percent in our everyday lives. To solve these applications, we will follow the same strategy we used in the section on decimal operations. We show it again here for easy reference.
HOW TO: Solve an application
- Step 1. Identify what you are asked to find and choose a variable to represent it.
- Step 2. Write a sentence that gives the information to find it.
- Step 3. Translate the sentence into an equation.
- Step 4. Solve the equation using good algebra techniques.
- Step 5. Check the answer in the problem and make sure it makes sense.
- Step 6. Write a complete sentence that answers the question.
Remember that whatever the application, once we write the sentence with the given information (Step 2), we can translate it to a percent equation and then solve it.
Do you pay a tax when you shop in your city or state? In many parts of the United States, sales tax is added to the purchase price of an item. See Figure \(\PageIndex{1}\). The sales tax is determined by computing a percent of the purchase price.
To find the sales tax multiply the purchase price by the sales tax rate. Remember to convert the sales tax rate from a percent to a decimal number. Once the sales tax is calculated, it is added to the purchase price. The result is the total cost—this is what the customer pays.

Figure \(\PageIndex{1}\) - The sales tax is calculated as a percent of the purchase price.
Definition: sales tax
The sales tax is a percent of the purchase price.
Sales Tax = Tax Rate • Purchase Price
Total Cost = Purchase Price + Sales Tax
Example \(\PageIndex{1}\):
Cathy bought a bicycle in Washington, where the sales tax rate was 6.5% of the purchase price. What was (a) the sales tax and (b) the total cost of a bicycle if the purchase price of the bicycle was $392?
Solution
(a)
| Identify what you are asked to find. | What is the sales tax? |
| Choose a variable to represent it. | Let t = sales tax. |
| Write a sentence that gives the information to find it. | The sales tax is 6.5% of the purchase price. |
| Translate into an equation. (Remember to change the percent to a decimal). |  |
| Simplify. | t = 25.48 |
| Check: Is this answer reasonable? | Yes, because the sales tax amount is less than 10% of the purchase price. |
| Write a complete sentence that answers the question. | The sales tax is $25.48. |
(b)
| Identify what you are asked to find. | What is the total cost of the bicycle? |
| Choose a variable to represent it. | Let c = total cost of bicycle. |
| Write a sentence that gives the information to find it. | The total cost is the purchase price plus the sales tax. |
| Translate into an equation. (Remember to change the percent to a decimal). |  |
| Simplify. | c = 417.48 |
| Check: Is this answer reasonable? | Yes, because the total cost is a little more than the purchase price. |
| Write a complete sentence that answers the question. | The total cost of the bicycle is $417.48. |
Exercise \(\PageIndex{1}\):
Find (a) the sales tax and (b) the total cost: Alexandra bought a television set for $724 in Boston, where the sales tax rate was 6.25% of the purchase price.
- Answer a
-
$45.25
- Answer b
-
$769.25
Exercise \(\PageIndex{2}\):
Find (a) the sales tax and (b) the total cost: Kim bought a winter coat for $250 in St. Louis, where the sales tax rate was 8.2% of the purchase price.
- Answer a
-
$20.50
- Answer b
- $270.50
Example \(\PageIndex{2}\):
Evelyn bought a new smartphone for $499 plus tax. She was surprised when she got the receipt and saw that the tax was $42.42. What was the sales tax rate for this purchase?
Solution
| Identify what you are asked to find. | What is the sales tax rate? |
| Choose a variable to represent it. | Let r = sales tax. |
| Write a sentence that gives the information to find it. | What percent of the price is the sales tax? |
| Translate into an equation. |  |
| Divide. | $$\dfrac{499r}{499} = \dfrac{42.42}{499}$$ |
| Simplify | r = 0.085 |
| Check. Is this answer reasonable? | Yes, because 8.5% is close to 10%. 10% of $500 is $50, which is close to $42.42. |
| Write a complete sentence that answers the question. | The sales tax rate is 8.5%. |
Exercise \(\PageIndex{3}\):
Diego bought a new car for $26,525. He was surprised that the dealer then added $2,387.25. What was the sales tax rate for this purchase?
- Answer
- 9%
Exercise \(\PageIndex{4}\):
What is the sales tax rate if a $7,594 purchase will have $569.55 of sales tax added to it?
- Answer
- 7.5%
Solve Commission Applications
Sales people often receive a commission, or percent of total sales, for their sales. Their income may be just the commission they earn, or it may be their commission added to their hourly wages or salary. The commission they earn is calculated as a certain percent of the price of each item they sell. That percent is called the rate of commission.
Definition: commission
A commission is a percentage of total sales as determined by the rate of commission.
commission = rate of commission • total sales
To find the commission on a sale, multiply the rate of commission by the total sales. Just as we did for computing sales tax, remember to first convert the rate of commission from a percent to a decimal.
Example \(\PageIndex{3}\):
Helene is a realtor. She receives 3% commission when she sells a house. How much commission will she receive for selling a house that costs $260,000?
Solution
| Identify what you are asked to find. | What is the commission? |
| Choose a variable to represent it. | Let c = the commission. |
| Write a sentence that gives the information to find it. | The commission is 3% of the price. |
| Translate into an equation. |
|
| Simplify. | c = 7800 |
| Change to percent form. | r = 8.5% |
| Check. Is this answer reasonable? | Yes. 1% of $260,000 is $2,600, and $7,800 is three times $2,600. |
| Write a complete sentence that answers the question. | Helene will receive a commission of $7,800. |
Exercise \(\PageIndex{5}\):
Bob is a travel agent. He receives 7% commission when he books a cruise for a customer. How much commission will he receive for booking a $3,900 cruise?
- Answer
- $273
Exercise \(\PageIndex{6}\):
Fernando receives 18% commission when he makes a computer sale. How much commission will he receive for selling a computer for $2,190?
- Answer
- $394.20
Example \(\PageIndex{4}\):
Rikki earned $87 commission when she sold a $1,450 stove. What rate of commission did she get?
Solution
| Identify what you are asked to find. | What is the rate of commission? |
| Choose a variable to represent it. | Let r = the rate of commission. |
| Write a sentence that gives the information to find it. | The commission is what percent of the sale? |
| Translate into an equation. |
|
| Divide. | $$\dfrac{87}{1450} = \dfrac{1450r}{1450}$$ |
| Simplify. | 0.06 = r |
| Change to percent form. | r = 6% |
| Check if this answer is reasonable. | Yes. A 10% commission would have been $145. The 6% commission, $87, is a little more than half of that. |
| Write a complete sentence that answers the question. | The commission was 6% of the price of the stove. |
Exercise \(\PageIndex{7}\):
Homer received $1,140 commission when he sold a car for $28,500. What rate of commission did he get?
- Answer
- 4%
Exercise \(\PageIndex{8}\):
Bernice earned $451 commission when she sold an $8,200 living room set. What rate of commission did she get?
- Answer
- 5.5%
Solve Discount Applications
Applications of discount are very common in retail settings Figure 6.8. When you buy an item on sale, the original price of the item has been reduced by some dollar amount. The discount rate, usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount, we multiply the discount rate by the original price. We summarize the discount model in the box below.

Figure 6.8 - Applications of discounts are common in everyday life. (credit: Charleston's TheDigitel, Flickr)
Definition: discount
An amount of discount is a percent off the original price.
amount of discount = discount rate • original price
sale price = original price − discount
The sale price should always be less than the original price. In some cases, the amount of discount is a fixed dollar amount. Then we just find the sale price by subtracting the amount of discount from the original price.
Example \(\PageIndex{5}\):
Jason bought a pair of sunglasses that were on sale for $10 off. The original price of the sunglasses was $39. What was the sale price of the sunglasses?
Solution
| Identify what you are asked to find. | What is the sale price? |
| Choose a variable to represent it. | Let s = the sale price. |
| Write a sentence that gives the information to find it. | The sale price is the original price minus the discount. |
| Translate into an equation. |  |
| Simplify. | s = 29 |
| Check if this answer is reasonable. | Yes. The sale price, $29, is less than the original price, $39. |
| Write a complete sentence that answers the question. | The sale price of the sunglasses was $29. |
Exercise \(\PageIndex{9}\):
Marta bought a dishwasher that was on sale for $75 off. The original price of the dishwasher was $525. What was the sale price of the dishwasher?
- Answer
- $450
Exercise \(\PageIndex{10}\):
Orlando bought a pair of shoes that was on sale for $30 off. The original price of the shoes was $112. What was the sale price of the shoes?
- Answer
- $82
In Example 6.29, the amount of discount was a set amount, $10. In Example 6.30 the discount is given as a percent of the original price.
Example \(\PageIndex{6}\):
Elise bought a dress that was discounted 35% off of the original price of $140. What was (a) the amount of discount and (b) the sale price of the dress?
Solution
(a) Before beginning, you may find it helpful to organize the information in a list. Original price = $140, Discount rate = 35%, Amount of discount = ?
| Identify what you are asked to find. | What is the amount of discount? |
| Choose a variable to represent it. | Let d = the amount of discount. |
| Write a sentence that gives the information to find it. | The discount is 35% of the original price. |
| Translate into an equation. | 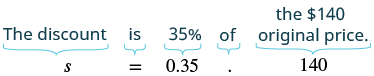 |
| Simplify. | d = 49 |
| Check if this answer is reasonable. | Yes. A $49 discount is reasonable for a $140 dress. |
| Write a complete sentence that answers the question. | The amount of discount was $49. |
(b) Original price = $140, Amount of discount = $49, Sale price = ?
| Identify what you are asked to find. | What is the sale price of the dress? |
| Choose a variable to represent it. | Let s = the sale price. |
| Write a sentence that gives the information to find it. | The sale price is the original price minus the discount. |
| Translate into an equation. |  |
| Simplify. | s = 91 |
| Check if this answer is reasonable. | Yes. The sale price, $91, is less than the original price, $140. |
| Write a complete sentence that answers the question. | The sale price of the dress was $91. |
Exercise \(\PageIndex{11}\):
Find (a) the amount of discount and (b) the sale price: Sergio bought a belt that was discounted 40% from an original price of $29.
- Answer a
-
$11.60
- Answer b
-
$17.40
Exercise \(\PageIndex{12}\):
Find (a) the amount of discount and (b) the sale price: Oscar bought a barbecue grill that was discounted 65% from an original price of
$395.
- Answer a
-
$256.75
- Answer b
-
$138.25
There may be times when you buy something on sale and want to know the discount rate. The next example will show this case.
Example \(\PageIndex{7}\):
Jeannette bought a swimsuit at a sale price of $13.95. The original price of the swimsuit was $31. Find the (a) amount of discount and (b) discount rate.
Solution
(a) Before beginning, you may find it helpful to organize the information in a list. Original price = $31, Amount of discount = ?, Sale price = $13.95
| Identify what you are asked to find. | What is the amount of discount? |
| Choose a variable to represent it. | Let d = the amount of discount. |
| Write a sentence that gives the information to find it. | The discount is the original price minus the sale price. |
| Translate into an equation. |  |
| Simplify. | d = 17.05 |
| Check if this answer is reasonable. | Yes. The $17.05 discount is less than the original price. |
| Write a complete sentence that answers the question. | The amount of discount was $17.05. |
(b) Before beginning, you may find it helpful to organize the information in a list. Original price = $31, Amount of discount = $17.05, Discount rate = ?
| Identify what you are asked to find. | What is the amount of discount? |
| Choose a variable to represent it. | Let r = the discount rate. |
| Write a sentence that gives the information to find it. | The discount is what percent of the original price? |
| Translate into an equation. |  |
| Divide. | $$\dfrac{17.05}{31} = \dfrac{r(31)}{31}$$ |
| Simplify. | 0.55 = r |
| Check if this answer is reasonable. | The rate of discount was a little more than 50% and the amount of discount is a little more than half of $31. |
| Write a complete sentence that answers the question. | The rate of discount was 55%. |
Exercise \(\PageIndex{13}\):
Find (a) the amount of discount and (b) the discount rate: Lena bought a kitchen table at the sale price of $375.20. The original price of the table was $560.
- Answer a
-
$184.80
- Answer b
-
33%
Exercise \(\PageIndex{14}\):
Find (a) the amount of discount and (b) the discount rate: Nick bought a multi-room air conditioner at a sale price of $340. The original price of the air conditioner was $400.
- Answer a
-
$60
- Answer b
-
15%
Solve Mark-up Applications
Applications of mark-up are very common in retail settings. The price a retailer pays for an item is called the wholesale price. The retailer then adds a mark-up to the wholesale price to get the list price, the price he sells the item for. The mark-up is usually calculated as a percent of the wholesale price. The percent is called the mark-up rate. To determine the amount of mark-up, multiply the mark-up rate by the wholesale price. We summarize the mark-up model in the box below.
Definition: mark-up
The mark-up is the amount added to the wholesale price.
amount of mark-up = mark-up rate • wholesale price
list price = wholesale price + mark up
The list price should always be more than the wholesale price.
Example \(\PageIndex{8}\):
Adam's art gallery bought a photograph at the wholesale price of $250. Adam marked the price up 40%. Find the (a) amount of mark-up and (b) the list price of the photograph.
Solution
(a)
| Identify what you are asked to find. | What is the amount of mark-up? |
| Choose a variable to represent it. | Let m = the amount of each mark-up. |
| Write a sentence that gives the information to find it. | The mark-up is 40% of the wholesale price. |
| Translate into an equation. |  |
| Simplify. | m = 100 |
| Check if this answer is reasonable. | Yes. The markup rate is less than 50% and $100 is less than half of $250. |
| Write a complete sentence that answers the question. | The mark-up on the photograph was $100. |
(b)
| Identify what you are asked to find. | What is the list price? |
| Choose a variable to represent it. | Let p = the list price. |
| Write a sentence that gives the information to find it. | The list price is the wholesale price plus the mark-up. |
| Translate into an equation. |  |
| Simplify. | p = 350 |
| Check if this answer is reasonable. | Yes. The list price, $350, is more than the wholesale price, $250. |
| Write a complete sentence that answers the question. | The list price of the photograph was $350. |
Exercise \(\PageIndex{15}\):
Jim's music store bought a guitar at wholesale price $1,200. Jim marked the price up 50%. Find the (a) amount of mark-up and (b) the list price.
- Answer a
-
600%
- Answer b
-
$1,800
Exercise \(\PageIndex{16}\):
The Auto Resale Store bought Pablo's Toyota for $8,500. They marked the price up 35%. Find the (a) amount of mark-up and (b) the list price.
- Answer a
-
$2,975
- Answer b
-
$11,475
Practice Makes Perfect
Solve Sales Tax Applications
In the following exercises, find (a) the sales tax and (b) the total cost.
- The cost of a pair of boots was $84. The sales tax rate is 5% of the purchase price.
- The cost of a refrigerator was $1,242. The sales tax rate is 8% of the purchase price.
- The cost of a microwave oven was $129. The sales tax rate is 7.5% of the purchase price.
- The cost of a tablet computer is $350. The sales tax rate is 8.5% of the purchase price.
- The cost of a file cabinet is $250. The sales tax rate is 6.85% of the purchase price.
- The cost of a luggage set $400. The sales tax rate is 5.75% of the purchase price.
- The cost of a 6 -drawer dresser $1,199. The sales tax rate is 5.125% of the purchase price.
- The cost of a sofa is $1,350. The sales tax rate is 4.225% of the purchase price.
In the following exercises, find the sales tax rate.
- Shawna bought a mixer for $300. The sales tax on the purchase was $19.50.
- Orphia bought a coffee table for $400. The sales tax on the purchase was $38.
- Bopha bought a bedroom set for $3,600. The sales tax on the purchase was $246.60.
- Ruth bought a washer and dryer set for $2,100. The sales tax on the purchase was $152.25.
Solve Commission Applications
In the following exercises, find the commission.
- Christopher sold his dinette set for $225 through an online site, which charged him 9% of the selling price as commission. How much was the commission?
- Michele rented a booth at a craft fair, which charged her 8% commission on her sales. One day her total sales were $193. How much was the commission?
- Farrah works in a jewelry store and receives 12% commission when she makes a sale. How much commission will she receive for selling a $8,125 ring?
- Jamal works at a car dealership and receives 9% commission when he sells a car. How much commission will he receive for selling a $32,575 car?
- Hector receives 17.5% commission when he sells an insurance policy. How much commission will he receive for selling a policy for $4,910?
- Denise receives 10.5% commission when she books a tour at the travel agency. How much commission will she receive for booking a tour with total cost $7,420?
In the following exercises, find the rate of commission.
- Dontay is a realtor and earned $11,250 commission on the sale of a $375,000 house. What is his rate of commission?
- Nevaeh is a cruise specialist and earned $364 commission after booking a cruise that cost $5,200. What is her rate of commission?
- As a waitress, Emily earned $420 in tips on sales of $2,625 last Saturday night. What was her rate of commission?
- Alejandra earned $1,393.74 commission on weekly sales of $15,486 as a salesperson at the computer store. What is her rate of commission?
- Maureen earned $7,052.50 commission when she sold a $45,500 car. What was the rate of commission?
- Lucas earned $4,487.50 commission when he brought a $35,900 job to his office. What was the rate of commission?
Solve Discount Applications
In the following exercises, find the sale price.
- Perla bought a cellphone that was on sale for $50 off. The original price of the cellphone was $189.
- Sophie saw a dress she liked on sale for $15 off. The original price of the dress was $96.
- Rick wants to buy a tool set with original price $165. Next week the tool set will be on sale for 40% off.
- Angelo's store is having a sale on TV sets. One set, with an original price of $859, is selling for $125 off.
In the following exercises, find (a) the amount of discount and (b) the sale price.
- Janelle bought a beach chair on sale at 60% off. The original price was $44.95
- Errol bought a skateboard helmet on sale at 40% off. The original price was $49.95.
- Kathy wants to buy a camera that lists for $389. The camera is on sale with a 33% discount.
- Colleen bought a suit that was discounted 25% from an original price of $245.
- Erys bought a treadmill on sale at 35% off. The original price was $949.95.
- Jay bought a guitar on sale at 45% off. The original price was $514.75.
In the following exercises, find (a) the amount of discount and (b) the discount rate. (Round to the nearest tenth of a percent if needed.)
- Larry and Donna bought a sofa at the sale price of $1,344. The original price of the sofa was $1,920.
- Hiroshi bought a lawnmower at the sale price of $240. The original price of the lawnmower is $300.
- Patty bought a baby stroller on sale for $301.75. The original price of the stroller was $355.
- Bill found a book he wanted on sale for $20.80. The original price of the book was $32.
- Nikki bought a patio set on sale for $480. The original price was $850.
- Stella bought a dinette set on sale for $725. The original price was $1,299.
Solve Mark-up Applications
In the following exercises, find (a) the amount of the mark-up and (b) the list price.
- Daria bought a bracelet at wholesale cost $16 to sell in her handicraft store. She marked the price up 45%.
- Regina bought a handmade quilt at wholesale cost $120 to sell in her quilt store. She marked the price up 55%.
- Tom paid $0.60 a pound for tomatoes to sell at his produce store. He added a 33% mark-up.
- Flora paid her supplier $0.74 a stem for roses to sell at her flower shop. She added an 85% mark-up.
- Alan bought a used bicycle for $115. After re-conditioning it, he added 225% mark-up and then advertised it for sale.
- Michael bought a classic car for $8,500. He restored it, then added 150% mark-up before advertising it for sale.
Everyday Math
- Coupons Yvonne can use two coupons for the same purchase at her favorite department store. One coupon gives her $20 off and the other gives her 25% off. She wants to buy a bedspread that sells for $195.
- Calculate the discount price if Yvonne uses the $20 coupon first and then takes 25% off.
- Calculate the discount price if Yvonne uses the 25% off coupon first and then uses the $20 coupon.
- In which order should Yvonne use the coupons?
- Cash Back Jason can buy a bag of dog food for $35 at two different stores. One store offers 6% cash back on the purchase plus $5 off his next purchase. The other store offers 20% cash back.
- Calculate the total savings from the first store, including the savings on the next purchase.
- Calculate the total savings from the second store.
- Which store should Jason buy the dog food from? Why?
Writing Exercises
- Priam bought a jacket that was on sale for 40% off. The original price of the jacket was $150. While the sales clerk figured the price by calculating the amount of discount and then subtracting that amount from $150, Priam found the price faster by calculating 60% of $150.
- Explain why Priam was correct.
- Will Priam's method work for any original price?
- Roxy bought a scarf on sale for 50% off. The original price of the scarf was $32.90. Roxy claimed that the price she paid for the scarf was the same as the amount she saved. Was Roxy correct? Explain.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
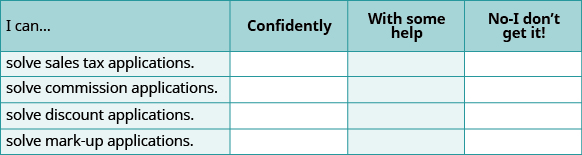
(b) What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."