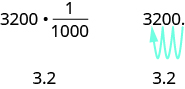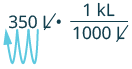In this section we will see how to convert among different types of units, such as feet to miles or kilograms to pounds. The basic idea in all of the unit conversions will be to use a form of 1, the multiplicative identity, to change the units but not the value of a quantity.
Make Unit Conversions in the U.S. System
There are two systems of measurement commonly used around the world. Most countries use the metric system. The United States uses a different system of measurement, usually called the U.S. system. We will look at the U.S. system first.
The U.S. system of measurement uses units of inch, foot, yard, and mile to measure length and pound and ton to measure weight. For capacity, the units used are cup, pint, quart and gallons. Both the U.S. system and the metric system measure time in seconds, minutes, or hours.
The equivalencies among the basic units of the U.S. system of measurement are listed in Table \(\PageIndex{1}\). The table also shows, in parentheses, the common abbreviations for each measurement.
Table \(\PageIndex{1}\)
| U.S. System Units |
| Length |
Volume |
|
1 foot (ft) = 12 inches (in)
1 yard (yd) = 3 feet (ft)
1 mile (mi) = 5280 feet (ft)
|
3 teaspoons (t) = 1 tablespoon (T)
16 Tablespoons (T) = 1 cup (C)
1 cup (C) = 8 fluid ounces (fl oz)
1 pint (pt) = 2 cups (C)
1 quart (qt) = 2 pints (pt)
1 gallon (gal) = 4 quarts (qt)
|
| Weight |
Time |
|
1 pound (lb) = 16 ounces (oz)
1 ton = 2000 pounds (lb)
|
1 minute (min) = 60 seconds (s)
1 hour (h) = 60 minutes (min)
1 day = 24 hours (h)
1 week (wk) = 7 days
1 year (yr) = 365 days
|
In many real-life applications, we need to convert between units of measurement. We will use the identity property of multiplication to do these conversions. We’ll restate the Identity Property of Multiplication here for easy reference.
For any real number a,
\[a \cdot 1 = a \qquad 1 \cdot a = a\]
To use the identity property of multiplication, we write 1 in a form that will help us convert the units. For example, suppose we want to convert inches to feet. We know that 1 foot is equal to 12 inches, so we can write 1 as the fraction \(\dfrac{1\; ft}{12\; in}\). When we multiply by this fraction, we do not change the value but just change the units. But \(\dfrac{12\; in}{1\; ft}\) also equals 1. How do we decide whether to multiply by \(\dfrac{1\; ft}{12\; in}\) or \(\dfrac{12\; in}{1\; ft}\)? We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert 60 inches to feet. If we choose the fraction that has inches in the denominator, we can eliminate the inches.
\[60\; \cancel{in} \cdot \dfrac{1\; ft}{12\; \cancel{in}} = 5\; ft\]
On the other hand, if we wanted to convert 5 feet to inches, we would choose the fraction that has feet in the denominator.
\[5\; \cancel{ft} \cdot \dfrac{12\; in}{1\; \cancel{ft}} = 60\; in\]
We treat the unit words like factors and ‘divide out’ common units like we do common factors.
HOW TO: MAKE UNIT CONVERSIONS
Step 1. Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
Step 2. Multiply.
Step 3. Simplify the fraction, performing the indicated operations and removing the common units.
Example \(\PageIndex{1}\):
Mary Anne is 66 inches tall. What is her height in feet?
Solution
| Convert 66 inches into feet. |
|
| Multiply the measurement to be converted by 1. |
66 inches • 1 |
| Write 1 as a fraction relating the units given and the units needed. |
$$66\; inches \cdot \dfrac{1\; foot}{12\; inches}$$ |
| Multiply. |
$$\dfrac{66\; inches\; \cdot 1\; foot}{12\; inches}$$ |
| Simplify the fraction. |
$$\dfrac{66\; \cancel{inches}\; \cdot 1\; foot}{12\; \cancel{inches}} = \dfrac{66\; feet}{12}$$ |
| |
5.5 feet |
Notice that the when we simplified the fraction, we first divided out the inches. Mary Anne is 5.5 feet tall.
Exercise \(\PageIndex{1}\):
Lexie is 30 inches tall. Convert her height to feet.
- Answer
-
2.5 feet
Exercise \(\PageIndex{2}\):
Rene bought a hose that is 18 yards long. Convert the length to feet.
- Answer
-
54 feet
When we use the Identity Property of Multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually this means we want the conversion fraction to have those units in the denominator.
Example \(\PageIndex{2}\):
Ndula, an elephant at the San Diego Safari Park, weighs almost 3.2 tons. Convert her weight to pounds.

Figure \(\PageIndex{1}\) (credit: Guldo Da Rozze, Flickr)
Solution
We will convert 3.2 tons into pounds, using the equivalencies in Table \(\PageIndex{1}\). We will use the Identity Property of Multiplication, writing 1 as the fraction \(\dfrac{2000\; pounds}{1\; ton}\)
| Multiply the measurement to be converted by 1. |
3.2 tons • 1 |
| Write 1 as a fraction relating tons and pounds. |
$$3.2\; tons\; \cdot \dfrac{2000\; lbs}{1\; tons}$$ |
| Simplify. |
$$\dfrac{3.2\; \cancel{tons}\; \cdot 2000\; lbs}{1\; \cancel{tons}}$$ |
| Multiply. |
6400 lbs |
.Ndula weighs almost 6,400 pounds.
Exercise \(\PageIndex{3}\):
Arnold’s SUV weighs about 4.3 tons. Convert the weight to pounds.
- Answer
-
8600 pounds
Exercise \(\PageIndex{4}\):
A cruise ship weighs 51,000 tons. Convert the weight to pounds.
- Answer
-
102,000,000 pounds
Sometimes to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.
Example \(\PageIndex{3}\):
Juliet is going with her family to their summer home. She will be away for 9 weeks. Convert the time to minutes.
Solution
To convert weeks into minutes, we will convert weeks to days, days to hours, and then hours to minutes. To do this, we will multiply by conversion factors of 1.
| Write 1 as \(\dfrac{7\; days}{1\; week}, \dfrac{24\; hours}{1\; day}, \dfrac{60\; minutes}{1\; hour}\). |
$$\dfrac{9\; wk}{1} \cdot \dfrac{7\; days}{1\; wk} \cdot \dfrac{24\; hr}{1\; day} \cdot \dfrac{60\; min}{1\; hr}$$ |
| Cancel common units. |
$$\dfrac{9\; \cancel{wk}}{1} \cdot \dfrac{7\; \cancel{\textcolor{blue}{days}}}{1\; \cancel{wk}} \cdot \dfrac{24\; \cancel{\textcolor{red}{hr}}}{1\; \cancel{\textcolor{blue}{day}}} \cdot \dfrac{60\; min}{1\; \cancel{\textcolor{red}{hr}}}$$ |
| Multiply. |
$$\dfrac{9 \cdot 7 \cdot 24 \cdot \cdot 60\; min}{1 \cdot 1 \cdot 1 \cdot 1} = 90,720\; min$$ |
Juliet will be away for 90,720 minutes.
Exercise \(\PageIndex{5}\)
The distance between Earth and the moon is about 250,000 miles. Convert this length to yards.
- Answer
-
440,000,000 yards
Exercise \(\PageIndex{6}\):
A team of astronauts spends 15 weeks in space. Convert the time to minutes.
- Answer
-
151,200 minutes
Example \(\PageIndex{4}\):
How many fluid ounces are in 1 gallon of milk?

Figure \(\PageIndex{2}\) (credit: www.bluewaikiki.com, Flickr)
Solution
Use conversion factors to get the right units: convert gallons to quarts, quarts to pints, pints to cups, and cups to fluid ounces.
| Multiply the measurement to be converted by 1. |
$$\dfrac{1\; gal}{1} \cdot \dfrac{4\; qt}{1\; gal} \cdot \dfrac{2\; pt}{1\; qt} \cdot \dfrac{2\; C}{1\; pt} \cdot \dfrac{8\; fl\; oz}{1\; C}$$ |
| Simplify. |
$$\dfrac{1\; \cancel{gal}}{1} \cdot \dfrac{4\; \cancel{qt}}{1\; \cancel{gal}} \cdot \dfrac{2\; \cancel{pt}}{1\; \cancel{qt}} \cdot \dfrac{2\; \cancel{C}}{1\; \cancel{pt}} \cdot \dfrac{8\; fl\; oz}{1\; \cancel{C}}$$ |
| Multiply. |
$$\dfrac{1 \cdot 4 \cdot 2 \cdot 2 \cdot 8\; fl\; oz}{1 \cdot 1 \cdot 1 \cdot 1 \cdot 1}$$ |
| Simplify. |
128 fluid ounces |
There are 128 fluid ounces in a gallon.
Exercise \(\PageIndex{7}\):
How many cups are in 1 gallon?
- Answer
-
16 cups
Exercise \(\PageIndex{8}\):
How many teaspoons are in 1 cup?
- Answer
-
48 teaspoons
Make Unit Conversions in the Metric System
In the metric system, units are related by powers of 10. The root words of their names reflect this relation. For example, the basic unit for measuring length is a meter. One kilometer is 1000 meters; the prefix kilo- means thousand. One centimeter is \(\dfrac{1}{100}\) of a meter, because the prefix centi- means one one-hundredth (just like one cent is \(\dfrac{1}{100}\) of one dollar).
The equivalencies of measurements in the metric system are shown in Table \(\PageIndex{2}\). The common abbreviations for each measurement are given in parentheses.
Table \(\PageIndex{2}\)
| Metric Measurements |
| Length |
Mass |
Volume/Capacity |
|
1 kilometer (km) = 1000 m
1 hectometer (hm) = 100 m
1 dekameter (dam) = 10 m
1 meter (m) = 1 m
1 decimeter (dm) = 0.1 m
1 centimeter (cm) = 0.01 m
1 millimeter (mm) = 0.001 m
|
1 kilogram (kg) = 1000 g
1 hectogram (hg) = 100 g
1 dekagram (dag) = 10 g
1 gram (g) = 1 g
1 decigram (dg) = 0.1 g
1 centigram (cg) = 0.01 g
1 milligram (mg) = 0.001 g
|
1 kiloliter (kL) = 1000 L
1 hectoliter (hL) = 100 L
1 dekaliter (daL) = 10 L
1 liter (L) = 1 L
1 deciliter (dL) = 0.1 L
1 centiliter (cL) = 0.01 L
1 milliliter (mL) = 0.001 L
|
|
1 meter = 100 centimeters
1 meter = 1000 millimeters
|
1 gram = 100 centigrams
1 gram = 1000 milligrams
|
1 liter = 100 centiliters
1 liter = 1000 milliliters
|
To make conversions in the metric system, we will use the same technique we did in the U.S. system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.
Have you ever run a 5 k or 10 k race? The lengths of those races are measured in kilometers. The metric system is commonly used in the United States when talking about the length of a race.
Example \(\PageIndex{7}\):
Nick ran a 10-kilometer race. How many meters did he run?

Figure \(\PageIndex{4}\) (credit: William Warby, Flickr)
Solution
We will convert kilometers to meters using the Identity Property of Multiplication and the equivalencies in Table 7.63.
| Multiply the measurement to be converted by 1. |
$$10\; \textcolor{red}{km}\; \cdot 1$$ |
| Write 1 as a fraction relating kilometers and meters. |
$$10\; \textcolor{red}{km}\; \cdot \dfrac{1000\; m}{1\; \textcolor{red}{km}}$$ |
| Simplify. |
$$\dfrac{10\; \cancel{\textcolor{red}{km}}\; \cdot 1000\; m}{1\; \cancel{\textcolor{red}{km}}}$$ |
| Multiply. |
$$10,000\; m$$ |
Nick ran 10,000 meters.
Exercise \(\PageIndex{13}\):
Sandy completed her first 5-km race. How many meters did she run?
- Answer
-
5000 m
Exercise \(\PageIndex{14}\):
Herman bought a rug 2.5 meters in length. How many centimeters is the length?
- Answer
-
250 cm
Example \(\PageIndex{8}\):
Eleanor’s newborn baby weighed 3200 grams. How many kilograms did the baby weigh?
Solution
We will convert grams to kilograms.
| Multiply the measurement to be converted by 1. |
$$3200\; \textcolor{red}{g}\; \cdot 1$$ |
| Write 1 as a fraction relating kilograms and grams. |
$$3200\; \textcolor{red}{g}\; \cdot \dfrac{1\; kg}{1000\; \textcolor{red}{g}}$$ |
| Simplify. |
$$3200\; \cancel{\textcolor{red}{g}}\; \cdot \dfrac{1\; kg}{1000\; \cancel{\textcolor{red}{g}}}$$ |
| Multiply. |
$$\dfrac{3200\; kilograms}{1000}$$ |
| Divide. |
$$3.2\; kilograms$$ |
The baby weighed 3.2 kilograms.
Exercise \(\PageIndex{15}\)
Kari’s newborn baby weighed 2800 grams. How many kilograms did the baby weigh?
- Answer
-
2.8 kilograms
Exercise \(\PageIndex{16}\)
Anderson received a package that was marked 45004500 grams. How many kilograms did this package weigh?
- Answer
-
4.5 kilograms
Since the metric system is based on multiples of ten, conversions involve multiplying by multiples of ten. In Decimal Operations, we learned how to simplify these calculations by just moving the decimal. To multiply by 10, 100, or 1000, we move the decimal to the right 1, 2, or 3 places, respectively. To multiply by 0.1, 0.01, or 0.001 we move the decimal to the left 1, 2, or 3 places respectively. We can apply this pattern when we make measurement conversions in the metric system.
In Example 7.51, we changed 3200 grams to kilograms by multiplying by 1 1000 (or 0.001). This is the same as moving the decimal 3 places to the left.
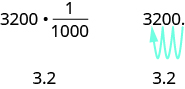
Example \(\PageIndex{9}\):
Convert: (a) 350 liters to kiloliters (b) 4.1 liters to milliliters.
Solution
(a) We will convert liters to kiloliters. In Table 7.63, we see that 1 kiloliter = 1000 liters.
| Multiply by 1, writing 1 as a fraction relating liters to kiloliters. |
$$350\; L\; \cdot \dfrac{1\; kL}{1000\; L}$$ |
| Simplify. |
$$350\; \cancel{L}\; \cdot \dfrac{1\; kL}{1000\; \cancel{L}}$$ |
| Move the decimal 3 units to the left. |
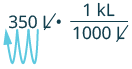 |
0.35 kL
(b) We will convert liters to milliliters. In Table 7.63, we see that 1 liter = 1000 milliliters.
| Multiply by 1, writing 1 as a fraction relating milliliters to liters. |
$$4.1\; L\; \cdot \dfrac{1000\; mL}{1\; L}$$ |
| Simplify. |
$$4.1\; \cancel{L}\; \cdot \dfrac{1000\; mL}{1\; \cancel{L}}$$ |
| Move the decimal 3 units to the left. |
 |
4100 mL
Exercise \(\PageIndex{17}\):
Convert: (a) 7.25 L to kL (b) 6.3 L to mL.
- Answer a
-
0.00725 kL
- Answer b
-
6300 mL
Exercise \(\PageIndex{18}\):
Convert: (a) 350 hL to L (b) 4.1 L to cL.
- Answer a
-
35,000 L
- Answer b
-
410 cL