2.5: Homework
- Last updated
- Aug 24, 2021
- Save as PDF
- Page ID
- 82986
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Submit homework separately from this workbook and staple all pages together. (One staple for the entire submission of all the unit homework)
- Start a new module on the front side of a new page and write the module number on the top center of the page.
- Answers without supporting work will receive no credit.
- Some solutions are given in the solutions manual.
- You may work with classmates but do your own work.
Hw #1
Let U = {a, c, e, m n, r, u, v, w, x, z} with subsets A, B, C and D defined below: A = {m, n, r, u, x} B = { a, c , r, u, x} C = {e, v, w, x, z } D = {a, c, z} Using correct notation, find the following, show all work
| a. B∩D | f. A−Cc | k. (A∩D)−Bc |
| b. A∩D | g. B−(A∩C) | l. n(A∪B) |
| c. C - B | h. Dc−(B∪C) | m. n(A) + n(B) |
| d. (A∪C)c | i. (A∩B)∩(C∪D) | n. n(D - C) |
| e. Dc∩B | j. (Bc∪D)c | o. n(B∩C) |
HW #2
Let U = {a, c, e, m n, r, u, v, w, x, z} with subsets A, B, C defined as follows:
| A = {m, n, r, u, v} | B = {r, u, w, x} | C = {n, r, x, c} |
Draw a Venn Diagram and place each element of the universe in the correct region
HW #3
Use deMorgan's Laws to rewrite each of the following:
| a. N∪Pc | b. Rc∩S |
HW #4
Use the distributive properties of sets to rewrite each of the following:
| a. (Ac∪E)∩(Ac∪F) | b. B∩(A∪C) |
HW #5
A survey was given to determine which of the three beverages (tea, milk and/or coffee) people drank each day. The results were as follows:
| 7 only drank coffee | 6 drank all three | 11 drank tea and coffee |
| 21 drank coffee | 4 drank none of the three | 9 drank neither coffee or tea |
| 21 drank tea | 1 drank only tea and milk |
| a. Draw a Venn diagram indicating how many people would belong in each region. Label the three sets with meaningful letters. |
| b. How many people were surveyed? |
| c. How many drank milk? |
| d. How many drank only coffee and milk? |
| e. How many drank only milk? |
| f. How many drank tea or coffee but not milk? |
| g. How many drank exactly two kinds of beverages? |
| h. How many didn’t drink milk or tea? |
HW #6
Take out your A–blocks and arrange them into subsets so that each subset only contains elements that have the same size and color.
| a. How many subsets are there? | b. How many pieces are in each subset? |
HW #7
Let A, B and C represent any sets. Answer True or False for the following statements. In order for a statement to be true, it must always be true. For each False statement, give an example of why it is False.
| a. B is always a subset of A∪B |
| b. (A−B)c=Ac−Bc |
| c. B is always a subset of A∩B |
| d. n(A∪B) = n(A) + n(B) |
| e. n(A∪B) = n(A) + n(B) – n(A∩B) |
| f. If n(A∪B) = n(A) + n(B), then A and B are disjoint. |
HW #8
Draw a Venn diagram and shade in the region that represents the following
| a. (C∪A)−B | b. (C∩B)∪A | c. (C∩B)−A |
| d. (A∪C)∩B | e. ˉA−(B∩C) | f. (B−A)∩(B−C) |
HW #9
Identify the shaded area of each Venn diagram by set notation.
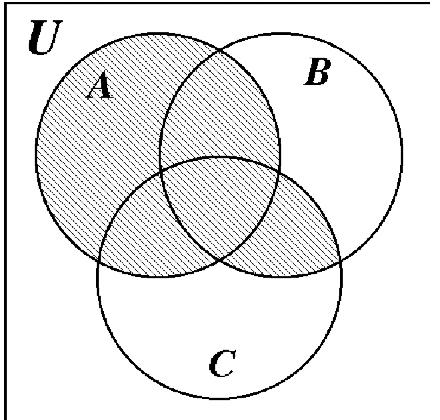 a. a. |
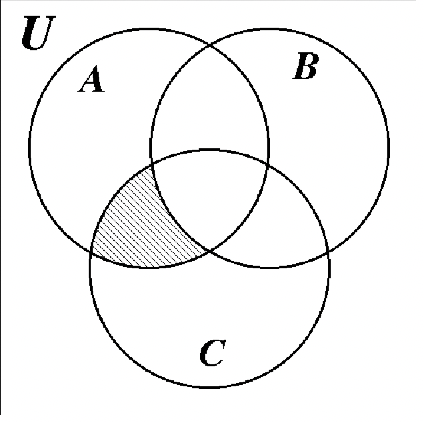 b. b. |
HW #10
List all possible subsets for each set given.
| a. { } | b. {a} | c. {a, b} | d. {a, b, c} |
HW #11
Let A = {1, 2, 4}, B = {(a, c), 5} and C = {x}. Find the following:
| a. A×A | a. A×B | c. B×C |
| d. C×A | a. C×C |
HW #12
Use your A–blocks to do this problem. Let X represent the set of large circles and Y represent the set of red circles. Using set notation and abbreviations, find the following:
| a. X - Y | b. X∩Y | c. X∪Y | d. Y - X |


