5.1: Definition and Properties
- Last updated
- Save as PDF
- Page ID
- 83002
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This exercise set presents a different, challenging way for you to look at multiplication. You will be using the Centimeter Strips (C-strips) to explore and discover the commutative, associative and distributive properties of multiplication. Below is a reminder of the different C-Strips we'll be working with along with the abbreviation used for each highlighted in bold:
| 1 cm by 1 cm | WHITE | 1 cm by 2 cm | RED |
| 1 cm by 3 cm | LIGHT GREEN | 1 cm by 4 cm | PURPLE |
| 1 cm by 5 cm | YELLOW | 1 cm by 6 cm | DARK GREEN |
| 1 cm by 7 cm | BLACK | 1 cm by 8 cm | BROWN |
| 1 cm by 9 cm | BLUE | 1 cm by 10 cm | ORANGE |
| 1 cm by 11 cm | SILVER | 1 cm by 12 cm | HOT PINK |
We will begin by defining a way to "multiply" two C-strips together. Consider multiplying the Purple C-strip by the Yellow C-Strip. Using abbreviations, we will write \(P \times Y\), which we will read aloud as "P cross Y". The first step in this "multiplication" is to place the first strip (P) down in a horizontal position and then to place the second strip (Y) underneath the first strip so that it is perpendicular to the first strip. The second step is to fill in more yellow C-strips alongside the one already there so that you form a rectangle of yellow strips where the length is the yellow strip and the width is the purple strip. Last, remove the horizontal strip (purple in this case) and form a train of the vertical strip(s) (yellow in this case). This train is \(P \times Y\) and is shown below. See the illustrations of the three steps.
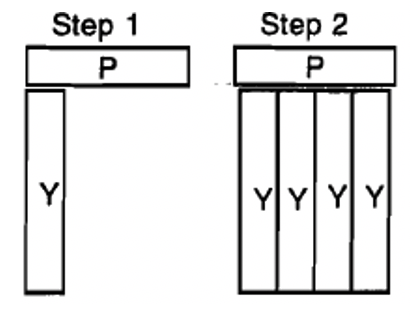

We say \(P \times Y\) is the train consisting of 4 yellow C-strips. It is important to notice that the answer is a train that is formed with only yellow strips, which is the second letter in the multiplication.
Exercise 1
a. Make the train \(P \times Y\) as explained above. Save it until you finish part d.
b. Find \(Y \times P\) by following the same procedure used to find \(P \times Y\), by doing the first two steps and showing them below.
| Step 1: | Step 2: |
c. This train you eventually end up with should consist of only purple C-strips. How many purple strips are there? Draw a picture of the train \(Y \times P\).
d. Place the two trains, \(P \times Y\) and \(Y \times P\), side by side and compare the lengths of the two trains. What do you notice?
To make notation simple, let's agree to say that two trains are equal if they have the same length. In other words, from what you discovered in Exercise 1, \(P \times Y = Y \times P\).
For the following exercises, describe the trains formed by doing the following multiplications with C-strips. You should physically form each train by going through the same steps used to multiply \(P \times Y\) on the previous page. For part a and b, fill in the first blank with a numeral (how many) and the second blank with a color. Save each train in order to answer part c. Use your observation to write the equations asked for in Exercise 1d. For instance, since you discovered \(P \times Y = Y \times P\), this translates to \(4 \times 5 = 5 \times 4\), since P is 4 cm long and Y is 5 cm long. Use this example to fill in blanks for exercises 2, 3 and 4.
Example a
Find \(P \times Y\). This train consists of
Example b
Find \(Y \times P\). This train consists of
Exercise 2
a. Find \(R \times D\). This train consists of _____ C-strips
b. Find \(D \times R\). This train consists of ______ C-strips
c. \(R \times D\) is made up of ____ white strips and \(D \times R\) is made up of _____ white strips.
d. What do you notice when you compare the lengths of the trains \(R \times D\) and \(D \times R\)?
e. From your work in parts a - d, write an equation including C-strips R and D; then translate the equation to one with numbers.
Exercise 3
a. Find \(K \times L\). This train consists of _____ C-strips
b. Find \(L \times K\). This train consists of _____ C-strips
c. \(K \times L\) is made up of ____ white strips and \(L \times K\) is made up of _____ white strips.
d. What do you notice when you compare the lengths of the trains \(K \times L\) and \(L \times K\)?
e. From your work in parts a - d, write an equation including C-strips K and L; then translate the equation to one with numbers.
Exercise 4
a. Find \(H \times W\). This train consists of _____ C-strips
b. Find \(W \times H\). This train consists of _____ C-strips
c. \(H \times W\) is made up of ____ white strips and \(W \times H\) is made up of ____ white strips.
d. What do you notice when you compare the lengths of the trains \(H \times W\) and \(W \times H\)?
e. From your work in parts a - d, write an equation including C-strips H and W; then translate the equation to one with numbers.
The above problems illustrate the commutative property of multiplication for trains.
The commutative property of multiplication for trains states that if s and t are any two trains, then \(s \times t = t \times s\)
Note: A train can consist of one or more C-strips. In other words, a single white (or any other color) C-strip is actually a train. There doesn't have to be a caboose and engine!
Exercise 5
Fill in the blanks to each of the following problems. To do this, take the color c-strip shown after the multiplication sign and make a train out of that color that is equal in length to the c-strip on the right side of the equal sign. Second, take the train and form it into a rectangle. Then find a c-strip that fits across the width of the rectangle. Write the abbreviation for that c-strip in the blank.
| a. ____ \(\times R = H\) | b. ____ \(\times P = P\) | c. ____ \(\times L = D\) |
| d. ____ \(\times R = N\) | e. ____ \(\times L = B\) | f. ____ \(\times W = K\) |
| g. ____ \(\times R = D\) | h. ____ \(\times D = H\) | i. ____ \(\times Y = O\) |
Exercise 6
a. Take out the Hot Pink (H) C-strip. Use your C-strips (one color at a time) to see if you can form a train made up of c-strips of the same color equal in length to the hot pink c-strip in other words, see if you can do it with all whites (always possible for any train), or all reds, or all light greens, etc. You should be able to make six different trains each train is made up of a single color. Draw a picture of each of these trains under the Hot Pink one shown. I've drawn two trains for you already one is simply the hot pink strip (a train consisting of just one c-strip), and a second is made up of three purple c-strips.
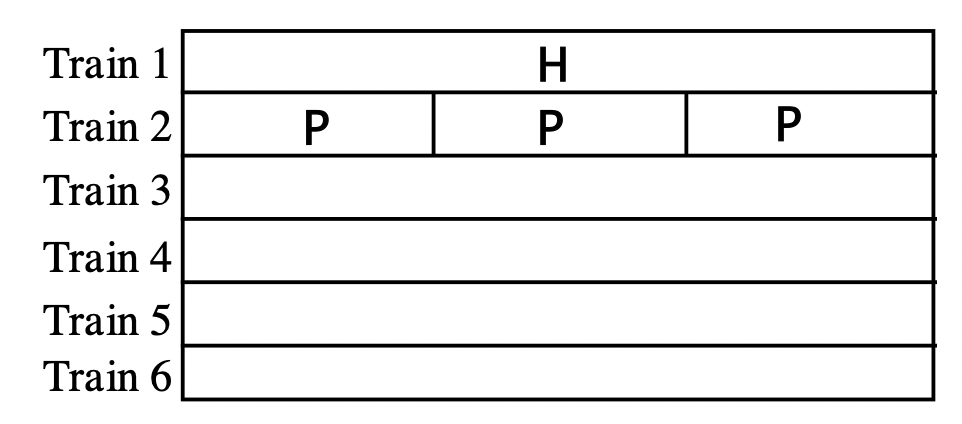
b. Your work from exercise 5 should help complete this exercise. Take each train, one at a time, and put each strip in a vertical position, but side by side to form a rectangle. Then, find a c-strip that fits across the width (or top) of the rectangle. This should tell you from which multiplication problem each train was formed. Write an equation using c-strips and then translate to an equation with numbers. For instance, for train 2, first I would make a rectangle out of the three purple c-strips. Next, I would try to find a c-strip to fit across the top, which would be light green. Therefore, train 2 was formed from the multiplication \(L \times P\) remember that since the train is formed with purple c-strips, P is the second letter in the multiplication. So, the equation in c-strips is \(L \times P = H\), and the numerical equivalent is \(3 \times 4 = 12\). Follow this same procedure for the other four trains you made in part a.
Train 1 illustrates the multiplication \(W \times H = H\), or \(1 \times 12 = 12\). (Note that if the hot pink strip is vertical, the white c-strip fits across the top.)
Train 2 illustrates the multiplication \(L \times P\) = H, or \(3 \times 4 = 12\)
Train 3 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = 12
Train 4 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = _____
Train 5 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = _____
Train 6 illustrates the multiplication ____ \(\times\) ____ = H, or ____ \(\times\) ____ = _____
Exercise 7
For train 2 in exercise 6, I made a train of purple c-strips equal in length to the hot pink c-strip. Now, make a train of purple c-strips equal in length to the brown (N) c-strip. Take the train of the purple c-strips and make it into a rectangle.
Which color c-strip measures across the width of this rectangle? ______
Put the answer (abbreviation for the c-strip) in the blank to solve the multiplication: ____ \(\times\) P = N.
Now, we'll explore more about the equations formed in exercise 5. Consider part a. You should have written \(D \times R = H\). This is analogous to the statement \(6 \times 2 = 12\). But, if you actually look at the original train that was formed to find the answer, you would see that there were 6 red c-strips that made a train equal in length to the hot pink c-strip. This gives rise to one of the whole number definitions of multiplication. Multiplication is really just the same thing as Repeated Addition.
Definition: Multiplication of Whole Numbers using the repeated addition approach
If a and b are whole numbers, then a \(\times\) b = b + b+ b+ b + ... + b, where there are a addends of b in this sum.
I like to think of using the definition like this:
3 \(\times\) 4 means 3 fours added together or 3 \(\times\) 4 = 4 + 4 + 4 = 12
4 \(\times\) 3 means 4 threes added together, or 4 \(\times\) 3 = 3 + 3 + 3 + 3 = 12
5 \(\times\) 2 means 5 twos added together, or 5 \(\times\) 2 = 2 + 2 + 2 + 2 + 2 = 10
2 \(\times\) 5 means 2 fives added together, or 2 \(\times\) 5 = 5 + 5 = 10
Note that although 3 \(\times\) 4 gives the same answer as 4 \(\times\) 3, it does not mean the same thing! One means 4 + 4 + 4 and the other means 3 + 3 + 3 + 3. Before we delve any further into this discussion, I want you to use the repeated addition definition to compute the following:
Exercise 8
Use the repeated addition definition of multiplication to compute the following. First, write out the meaning of the multiplication, and then compute the answer.
a. 6 \(\times\) 3 =
b. 2 \(\times\) 9 =
c. 9 \(\times\) 2 =
Now, it may seem obvious to you that 3 \(\times\) 4 is the same answer as 4 \(\times\) 3. That's because you've no doubt been using the commutative property of addition for years. Whether or not you really thought about why it was true is another thing. But, although 3 \(\times\) 4 gives the same answer as 4 \(\times\) 3, it does not mean the same thing. One means 4 + 4 + 4 and the other means 3 + 3 + 3 + 3. To a child just learning about addition and multiplication, there is no reason for them to conclude that one sum (4 + 4 + 4) happens to give the same answer as the other sum (3 + 3 + 3 + 3). For instance, if I was asked to compute the following two sums, it wouldn't be evident to me at all that the answer to each would be end up being the same:
| 17 + 17 + 17 + 17 and 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 |
Actually, I find it quite amazing that they are equal. But, indeed they are, because the first sum comes from the multiplication problem 4 \(\times\) 17 (since there are 4 seventeens added together), and the second sum comes from the multiplication problem 17 \(\times\) 4 (since there are 17 fours added together). Later, when we discuss a more geometrical definition for multiplication, it becomes obvious why the commutative property of multiplication is true.
The commutative property of multiplication for whole numbers states that if a and b are any two numbers, then
\[a \times b = b \times a. \nonumber \]
So, the very exciting thing about the commutative property of multiplication is that, given a problem like 100 \(\times\) 7, where it would take a long time to write out and compute the answer using the strict definition of multiplication by adding 7 over and over again, we can use our knowledge of the commutative property, that is 100 \(\times\) 7 = 7 \(\times\) 100, and compute the second multiplication instead. Wouldn't you agree that 100 + 100 + 100 + 100 + 100 + 100 + 100 is quicker and easier to compute than adding together 100 sevens? Thank goodness for the commutative property of multiplication!!!
Before going on to another property, let's practice verifying that the commutative property of multiplication is true for some numbers by using the repeated addition definition of multiplication. The commutative property requires two numbers (they don't have to be two different numbers) and there are two sides of an equation to verify. The difference between the expressions a \(\times\) b and b \(\times\) a is that the order of the numbers is different. Remember that the commutative property means there has been an order change. To verify the commutative property of multiplication, you need to use the repeated addition definition of multiplication and add from left to right, one number at a time. The next example shows how to verify the commutative property of multiplication, given a set of two numbers.
Example
Verify the commutative property of multiplication is true for the given set of numbers. You'll have to remember how to add in base six to do part b.
a. {5, 3}
Solution
I need to show \(5 \times 3 = 3 \times 5\). Since \(5 \times 3\) = 3 + 3 + 3 + 3 + 3 = 6 + 3 + 3 + 3 = 9 + 3 + 3 = 12 + 3 = 15 and since \(3 \times 5\)= 5 + 5 + 5 = 10 + 5 = 15, then \(5 \times 3 = 3 \times 5\), because both equal 15.
b. {\(3_{\text{six}}, 4_{\text{six}}\)}
Solution
I need to show \(3_{\text{six}} \times 4_{\text{six}} = 4_{\text{six}} \times 3_{\text{six}}\) Since \(3_{\text{six}} \times 4_{\text{six}} = 4_{\text{six}} + 4_{\text{six}} + 4_{\text{six}} = 12_{\text{six}} + 4_{\text{six}} = 20_{\text{six}}\) and since \(4_{\text{six}} \times 3_{\text{six}} = 3_{\text{six}} + 3_{\text{six}} + 3_{\text{six}} + 3_{\text{six}} = 10_{\text{six}} + 3_{\text{six}} + 3_{\text{six}} = 13_{\text{six}} + 3_{\text{six}} = 20_{\text{six}}\), then \(3_{\text{six}} \times 4_{\text{six}} = 4_{\text{six}} \times 3_{\text{six}}\), because both equal \(20_{\text{six}}\).
Exercise 9
Verify the commutative property of multiplication by writing an equation that must be true and using the repeated addition definition of multiplication is true using the given set of numbers. Simplify each expression separately; then show they are equal.
| a. {4, 3} |
| b. {\(2_{\text{five}}\), \(3_{\text{five}}\)} |
| c. Make up a set in a base other than 10 and verify the commutative property of multiplication. |
We can also use the repeated addition definition of multiplication to multiply in other numeration systems. Study the following examples and then work through the problems in exercise 10.
Example in Tally
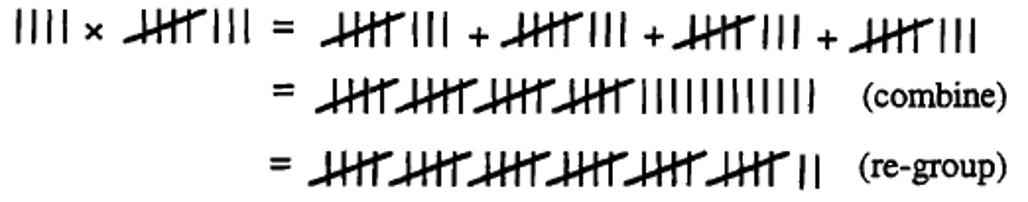
Example in Egyptian
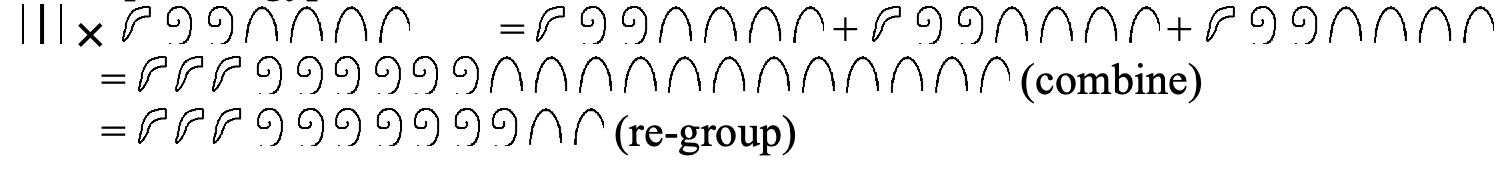
Example in Mayan
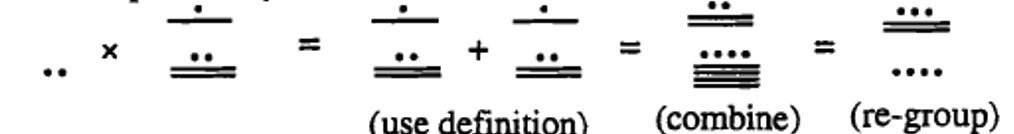
Notice that all of these examples are done completely in the numeration system given. All of the steps are shown in that numeration system. This is how you should do the problems in exercise 10. If you want, you can check the answer after you complete the problem by converting to base ten. For instance, the Mayan example in base ten is 2 \(\times\) 132. So the answer should be 264. If you convert the final answer to base ten, it is also 264.
Exercise 10
Use the repeated addition definition of multiplication to compute the following. Make sure you write out the meaning of the multiplication in the system given (see examples on previous page), showing all of the work and exchanges (if necessary), to compute the answer. Do not do the problem in base ten, although you can use base ten to check the answer when you are done.
|
a. 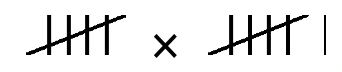 |
|
b. 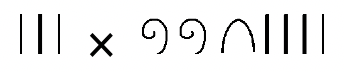 |
|
c. 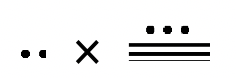 |
Exercise 11
Next, we will form the trains for \((R \times L) \times P\) and for \(R \times (L \times P)\). We can only work on one at a time. In both cases, you must do what's inside the parentheses first.
a. First, we'll do \((R \times L) \times P\). Begin by forming the train \(R \times L\) to use in part b.
b. Next, we need to form the train \((R \times L) \times P\). The first part, \(R \times L\), which you formed in part a, should be in a horizontal position, and the purple c-strip goes underneath it, perpendicular to the train \(R \times L\). Note that although \(R \times L\) is made up of more than one c-strip, it still forms one train across the top. In the space to the right, draw a picture of what this looks like so far.
c. Do the multiplication by filling in the rest of the purple c-strips in the vertical position under the train \(R \times L\); then form a train out of the rectangle of purple c-strips. Keep this train until you have finished all of exercise 11. How many purple c-strips are in the train formed by doing the multiplication \((R \times L) \times P\)?
d. Now, we'll do \(R \times (L \times P)\). Begin by forming the train \(L \times P\) to use in part e.
e. Next, form the train \(R \times (L \times P)\). Put the first part, R, in the horizontal position. The second part, \(L \times P\), formed in part d, should go in the vertical position as one long train, underneath and perpendicular to the train R. Don't separate the purple strips in \(L \times P\) line up as one long vertical train (made up of more than one purple C-strip) under the red c-strip. To the right, draw a picture of what this looks like so far.
f. Do the multiplication by filling in the rest of the purple c-strips to form the rectangle; then make a train out of the rectangle of purple c-strips. How many purple c-strips are in the train formed by doing the multiplication \(R \times (L \times P)\)?
g. Compare the length of train \((R \times L) \times P\), from part c with length of train \(R \times (L \times P)\), from part f. What do you notice?
h. From your observation, write an equation using the c-strips:
i. Translate the equation from part h to one with numbers:
j. Write the left side of the equation you wrote down in part i (which has numbers, not c-strips), and simplify by following the order of operations do what is in parentheses first. Then, do the same for the right side of the equation.
Left side:
Right side:
k. Are the two expressions you simplified in part (j) equal? If so, you have verified the equation from part (i) is true
Exercise 12
Next, we will form the trains for (\(Y \times R) \times L\) and for \(Y \times (R \times L)\).
a. First, we'll do (\(Y \times R) \times L\). Begin by forming the train \(Y \times R\).
b. Next, we need to form the train (\(Y \times R) \times L\). The first part, \(Y \times R\), which you formed in part a, should be in a horizontal position, and the light green c-strip should go underneath it, perpendicular to the train \(Y \times R\). Note that although \(Y \times R\) is made up of more than one c-strip, it still forms one train that is across the top. That's okay. Below, draw a picture of what this looks like so far.
c. Do the multiplication by filling in the rest of the light green c-strips and then making a train out of the rectangle of light green c-strips. Keep this train until you have finished all of exercise 12. How many light green c-strips are in the train formed by doing the multiplication \((Y \times R) \times L\) ?
d. Now, we'll do \(Y \times (R \times L)\). Begin by forming the train \(R \times L\).
e. Next, form the train \(Y \times (R \times L)\). Put the first part, Y, in the horizontal position. The second part, \(R \times L\), formed in part d, should go in the vertical position as one long train, underneath and perpendicular to the train Y. Don't separate the light green strips in \(R \times L\) line up as one long vertical train (made up of more than one light green C-strip) under the yellow c-strip. To the right, draw a picture of what this looks like so far.
f. Do the multiplication by filling in the rest of the light green c-strips to form the rectangle, and then making a train out of the rectangle of light green c-strips. How many light green c-strips are in the train formed by the multiplication \(Y \times (R \times L)\)?
g. Compare the length of train \((Y \times R) \times L\), from part c with the length of train \(Y \times (R \times L)\), from part f. What do you notice?
h. From your observation, write an equation using the c-strips:
i. Translate the equation from part h to one with numbers:
j. Write the left side of the equation you wrote down in part i (which has numbers, not c-strips), and simplify by following the order of operations do what is in parentheses first. Then, do the same for the right side of the equation.
Left side:
Right side:
k. Are the two expressions you simplified in part (j) equal? If so, you have verified the equation from part (i) is true.
Exercises 11 and 12 illustrate the associative property of multiplication for trains.
The associative property of multiplication for trains states that if r, s and t are any three trains, then \((r \times s) \times t = r \times (s \times t\)).
Before going on to any more properties, we'll practice verifying that the associative property of multiplication is true for some numbers in base ten later on, we'll do it in other bases, too. The associative property requires three numbers (they don't have to be three different numbers) and there are different expressions on each side of the equation. The difference between the left and right sides is that the parentheses are around a different pair of numbers. Remember that the associative property means there is a parentheses change, whereas the commutative property means there has been an order change. To verify, you need to use the order of operations when simplifying each side. If each expression simplifies to same thing, the equation is true. In the order of operations, you always simplify what is in parentheses first. The following are some examples of how to verify the associative property of multiplication, given a set of three numbers.
The associative property of multiplication for whole numbers states that if a, b and c are any three numbers, then \(( a \times b ) \times c = a \times ( b \times c )\).
Example 1
Verify the associative property of multiplication is true using the three numbers {4, 5, 7} in your example.
Note: Since the associative property states \((a \times b) \times c = a \times (b \times c)\), one of the numbers given is put in for a, the other for b and the other for c. The choice is yours. For example, we can show any of the following six equations are true:
| a. \((4 \times 5) \times 7 = 4 \times (5 \times 7)\) or d. \((4 \times 7) \times 5 = 4 \times (7 \times 5)\) |
| b. \((5 \times 4) \times 7 = 5 \times (4 \times 7)\) or e. \((7 \times 4) \times 5 = 7 \times (4 \times 5)\) |
| c. \((7 \times 5) \times 4 = 7 \times (5 \times 4)\) or f. \((5 \times 7) \times 4 = 5 \times (7 \times 4)\). |
If this was a question on a test, you would only have to verify one of the six equations shown there are always six possibilities one might choose, depending on which numbers you put in for a, b or c. I will show you how to do it if you decided to verify the equation (e). I'll also verify it for another equation (f). Then, for practice, you get to verify the other four equations.
One Solution to Example 1: I'll show: \((7 \times 4) \times 5 = 7 \times (4 \times 5)\)
Left side: \((7 \times 4) \times 5 = 28 \times 5 = 140\) and Right side: \(7 \times (4 \times 5) = 7 \times 20 = 140\)
Since I used the order of operations to simplify each expression, and both expressions are equal, the associative property is true using the numbers 4, 5 and 7.
Here is a different way to verify it using a different equation.
Another Solution to Example 1: I'll show: \((5 \times 7) \times 4 = 5 \times (7 \times 4)\)
Left side: \((5 \times 7) \times 4 = 35 \times 4 = 140\) and Right side: \(5 \times (7 \times 4) = 5 \times 28 = 140\)
Since I used the order of operations to simplify each expression, and both expressions are equal, the associative property is true using the numbers 4, 5 and 7.
Exercise 13
Verify the associative property of multiplication is true using the numbers 4, 5 and 7, by doing the order of operations on each side. Do this four times, using the equations a, b, c and then d, as shown on the previous page.
| a. Verify: \((4 \times 5) \times 7 = 4 \times (5 \times 7)\) |
| b. Verify: \((5 \times 4) \times 7 = 5 \times (4 \times 7)\) |
| c. Verify: \((7 \times 5) \times 4 = 7 \times (5 \times 4)\) |
| d. Verify: \((4 \times 7) \times 5 = 4 \times (7 \times 5)\) |
To verify the associative property of multiplication is true by example, first you must write an equation that must be true using any three numbers (or by using three particular numbers given to you.) Then, by doing the order of operations on each side (each individual expression), you must show each side of the equation gives the same result.
Example 2
Verify the associative property is true using the numbers 10, 8 and 3.
a. I will show this equation is true: \((10 \times 8) \times 3 = 10 \times (8 \times 3)\)
Since \((10 \times 8) \times 3 = 80 \times 3 = 240\) and \(10 \times (8 \times 3) = 10 \times 24 = 240\), then the equation \((10 \times 8) \times 3 = 10 \times (8 \times 3)\) is true.
Exercise 14
Verify the associative property is true using the numbers given.
a. {9, 7, 6}
b. any three numbers of your choice.
Time to work on another property...
STEP 1: Form the train \(P \times (R + L)\). To do this, the purple strip should be place in a horizontal position, and the train R + L should be placed in a vertical position underneath the purple c-strip. Then, the rectangle needs to filled in. Lastly, make a long train out of the rectangle. Note that this train is made up of 8 c-strips (4 reds and 4 light greens). Save this train.
STEP 2: Form two trains: \(P \times R\) and \(P \times L\). Then add the two trains together (in other words, \(P \times R + P \times L)\) to form one long train. Note that this train is made up of 8 c-strips (4 reds and 4 light greens). Compare the length of the train formed in Step 1 with this train. Are they are the same length? Are they made up of the same exact c-strips?
We have just shown and verified that \(P \times (R + L) = P \times R + P \times L\).
Exercise 15
a. Form the train \(L \times (P + Y)\) by first forming the train P + Y. Then do the multiplication \(L \times (P + Y)\). Exactly what c-strips make up this train?
b. Form the train \(L \times P\) and \(L \times Y\). Now add them together to form one long train. Exactly what c-strips make up this train?
c. Compare the trains from part a and b, and write an equation (with c-strips).
d. Translate the equation from part c by writing an equation using numbers.
e. Verify the equation you wrote in part d by first simplifying the left hand side of the equation using the order of operations and then by simplifying the right hand side as well. If the answer to each expression is the same, you have verified the equation.
left side:
right side:
Exercise 16
a. Form the train \(R \times (W + D)\) by first forming the train W + D. Then do the multiplication \(R \times (W + D)\). Exactly what c-strips make up this train?
b. Form the train \(R \times W\) and \(R \times D\). Now add them together to form one long train. Exactly what c-strips make up this train?
c. Compare the trains from part a and b, and write an equation (with c-strips).
d. Translate the equation from part c by writing an equation using numbers.
e. Verify the equation you wrote in part d by first simplifying the left hand side of the equation using the order of operations and then by simplifying the right hand side as well. If the answer to each expression is the same, you have verified the equation.
left side:
right side:
The above problems illustrate the distributive property of multiplication over addition for trains.
The distributive property of multiplication over addition for trains states that if r, s and t are any three trains (each train may be made up of one or more c-strips), then \(r \times (s + t) = (r \times s) + (r \times t)\).
Now, it's time to practice verifying the distributive property of multiplication over addition is true for some numbers in base ten — later on, we'll do it in other bases, too. The distributive property requires three numbers (they don't have to be three different numbers) and there are two sides of an equation to verify. Note the difference between the left and right sides. To verify, you need to use the order of operations when simplifying each side. In the order of operations, you always simplify what is in parentheses first. If each expression simplifies to same thing, the equation is true. The following are some examples of how to verify the distributive property of multiplication, given a set of three numbers.
The distributive property of multiplication over addition for whole numbers states that if a, b and c are any three numbers, then \(a \times (b + c) = (a \times b) + (a \times c)\).
Example 1
Verify the distributive property of multiplication is true using the three numbers {4, 5, 7} in your example.
Note: Since the distributive property states \(a \times (b + c) = (a \times b) + (a \times c)\), one of the numbers given is put in for a, the other for b and the other for c. The choice is yours. For example, we can show any of the following six equations are true:
| a. \(4 \times (5 + 7) = (4 \times 5) + (4 \times 7)\) or d. \(5 \times (7 + 4) = (5 \times 7) + (5 \times 4)\) |
| b. \(4 \times (7 + 5) = (4 \times 7) + (4 \times 5)\) or e. \(7 \times (4 + 5) = (7 \times 4) + (7 \times 5)\) |
| c. \(5 \times (4 + 7) = (5 \times 4) + (5 \times 7)\) or f. \(7 \times (5 + 4) = (7 \times 5) + (7 \times 4)\) |
If this was a question on a test, you would only have to verify one of the six equations shown. There are always six possibilities one might choose, depending on which numbers you put in for a, b or c. I will show you how to do it if you decided to verify the equation (c). I'll also verify it for another equation (f). Then, for practice, you get to verify the other four equations.
One Solution to Example 1: I'll show: \(5 \times (4 + 7) = (5 \times 4) + (5 \times 7)\)
Left side: \(5 \times (4 + 7) = 5 \times (11) = 55\) and Right side: \((5 \times 4) + (5 \times 7) = 20 + 35 = 55\)
Since I used the order of operations to simplify each expression, and both expressions are equal, the distributive property is true using the numbers 4, 5 and 7.
Here is a different way to verify it using a different equation.
Another Solution to Example 1: I'll show: \(7 \times (5 + 4) = (7 \times 5) + (7 \times 4)\)
Left side: \(7 \times (5 + 4) = 7 \times 9 = 63\) and Right side: \((7 \times 5) + (7 \times 4) = 35 + 28 = 63\)
Since I used the order of operations to simplify each expression, and both expressions are equal, the distributive property is true using the numbers 4, 5 and 7.
Exercise 17
Verify the distributive property of multiplication is true using the numbers 4, 5 and 7, by doing the order of operations on each side. Do this four times, using the equations a, b, d and then e, as shown on the previous page.
| a. Verify: \(4 \times (5 + 7) = (4 \times 5) + (4 \times 7)\) |
| b. Verify: \(4 \times (7 + 5) = (4 \times 7) + (4 \times 5)\) |
| c. Verify: \(5 \times (7 + 4) = (5 \times 7) + (5 \times 4)\) |
| d. Verify: \(7 \times (4 + 5) = (7 \times 4) + (7 \times 5)\) |
To verify the distributive property of multiplication is true by example, first you must write an equation that must be true using any three numbers (or by using three particular numbers given to you.) Then, by doing the order of operations on each side (each individual expression), you must show each side of the equation gives the same result.
Example 2
Verify the distributive property is true using the numbers 10, 8 and 5.
a. I will show this equation is true: \(10 \times (8 + 5) = (10 \times 8) + (10 \times 5)\)
Solution
Since \(10 \times (8 + 5) = 10 \times 13\) and \((10 \times 8) + (10 \times 5) = 80 + 50\), then the equation \(10 \times (8 + 5) = (10 \times 8) + (10 \times 5)\) is true.
Exercise 18
Verify the distributive property of multiplication over addition is true for the three numbers specified:
| a. {7, 8, 12} |
| b. {28, 65, 35} |
| c. any three numbers of your choice. |
Exercise 19
Use the definition of multiplication for trains to compute the following. Then translate to make an equation using numbers.
a. \(W \times R\) = _____ translates to _______________
b. \(W \times B\) = _____ translates to _______________
c. \(W \times D\) = _____ translates to _______________
d. \(W \times S\) = _____ translates to _______________
e. \(N \times W\) = _____ translates to _______________
f. \(H \times W\) = _____ translates to _______________
Exercise 19 illustrates that 1 is the identity element for multiplication. In other words, for any number m, \(\bf m \times 1 = m\) and \(\bf 1 \times m = m\).
Exercise 20
The identity element for multiplication if we are referring to trains is what you fill in the blank to make the following statement true. Fill in the blanks to find the identity.
For any train t, \(\bf t \times\) _____ \(\bf = t\) and _____ \(\bf \times t = t\).
The distributive property of multiplication over addition is used quite often to simplify arithmetic problems. Consider the following examples:
Someone who needed to multiply \(57 \times 102\) might find it easier to think of the problem as \(57 \times (100 + 2) = (57 \times 100) + (57 \times 2) = 5700 + 114 = 5814\).
Someone who needed to compute \(47 \times 38 + 47 \times 62\) might realize this is really just the same as \(47 \times (38 + 62) = 47 \times 100 = 4700\).
This next example illustrates that multiplication also distributes over subtraction:
Someone who needed to multiply \(38 \times 99\) might find it easier to think of the problem as \(38 \times (100 - 1) = (38 \times 100) - (38 \times 1) = 3800 - 38 = 3762\).
Exercise 21
Use the distributive property of multiplication over addition (or subtraction) to rewrite the following problems. Then, simplify. For d, e and f, make up three of your own problems where it would be easier to use the distributive property first before simplifying. Show how to use the property and simplify.
| a. \(764 \times 999\) |
| b. \(324 \times 102\) |
| c. \(83 \times 74 + 83 \times 26\) |
| d. |
| e. |
| f. |
Exercise 22
So far, you have worked with three operations; addition, subtraction and multiplication. You have learned many properties. Take a little time to reflect on and review these by writing the properties or answering the questions as stated below:
| a. State the associative property of multiplication and provide an example. |
| b. State the commutative property of addition and provide an example. |
| c. State the identity element for addition and what it means and provide an example. |
| d. State the commutative property of multiplication and provide an example. |
| e. State the distributive property of multiplication over addition and provide an example. |
| f. State the identity element for multiplication and provide an example. |
| g. Provide a counterexample to show that subtraction is not commutative |
| h. State the associative property of addition. |
| i. Provide a counterexample to show that subtraction is not associative. |
There is another way to define multiplication using Set Theory. In order to do this, we have to remember how to take the Cartesian product of two sets, A and B.
The Cartesian product of set A with set B, which is written \(A \times B\) and is read as "A cross B" is the set of all possible ordered pairs (a,b), where \(a \times A\) and \(b \times B\).
If you are finding the Cartesian product, the answer is a set that contains ordered pairs.
Example 1
If A = {x, y, z} and B = {a, b}, find \(A \times B\).
Solution
\(A \times B\) = {(x, a), (x, b), (y, a), (y, b), (z, a), (z, b)}
Example 2
If E = {1, 2} and F = {2, 3}, find \(E \times F\).
Solution
\(E \times F\) = {(1, 2), (1, 3), (2, 2), (2, 3)}
Exercise 23
Write the Cartesian product. Each answer is a set containing ordered pairs!
a. {3, 4} \(\times\) {2, 6} = _______
b. {6, 7, 8, 9} \(\times\) {5} = ________
c. {r, s, t} \(\times\) { } = _________
d. {a} \(\times\) {a} = _________
e. {x, y} \(\times\) {x, y} = ________
f. {1, 3, 5} \(\times\) {1, 3, 5} = ________
Set Theory Definition for Multiplying two whole numbers:
For any two sets A and B, \(\bf n(A) \cdot n(B) = n(A \times B)\).
In other words, to multiply two numbers, a and b, write one set A which has a elements in it and another set B that has b elements in it. To find the product, write the Cartesian
product of A and B and count the elements in the set.
Note: There are no restrictions on what elements you choose for sets A and B. They can be disjoint or they can have elements in common. It’s up to you.
Example 1
Use the set theory definition of multiplication to show that \(3 \cdot 2 = 6\)
Solution
Let A = {v, w, x} and B = {1, 2}. Since n(A) = 3 and n(B) = 2, then
\(\begin{aligned} 3 \cdot 2 && = n(A) \cdot n(B) && \text{ by substituting n(A)for 3 and n(B)for 2} \\
&& = n(A \times B) && \text{ by the set theory definition of multiplication} \\
&& = n(\{(v,1), (v, 2), (w, 1), (w, 2), (x, 1), (x, 2)\}) && \text{ by computing } A \times B \\
&& =6 && \text{ by counting the elements in } A \times B \end{aligned}\)
Therefore, \(3 \cdot 2 = 6\).
Example 2
Use the set theory definition of multiplication to show that \(1 \cdot 3 = 3\)
Solution
Let A = {v} and B = {1, 2, 3}. Since n(A) = 1 and n(B) = 3, then
\(\begin{aligned} 1 \cdot 3 && = n(A) \cdot n(B) && \text{ by substituting n(A)for 1 and n(B)for 3} \\
&& = n(A \times B) && \text{ by the set theory definition of multiplication} \\
&& = n(\{(v,1), (v, 2), (v, 3)\}) && \text{ by computing } A \times B \\
&& = 3 && \text{ by counting the elements in } A \times B \end{aligned}\)
Therefore, \(1 \cdot 3 = 3\)
Example 3
Use the set theory definition of multiplication to show that \(2 \cdot 0 = 0\)
Solution
Let A = {v, w} and B = { }. Since n(A) = 2 and n(B) = 0, then
\(\begin{aligned} 2 \cdot 0 && = n(A) \cdot n(B) && \text{ by substituting n(A)for 2 and n(B)for 0} \\
&& = n(A \times B) && \text{ by the set theory definition of multiplication} \\
&& = n(\{ \ \}) && \text{ by computing } A \times B \\
&& = 0 && \text{ by counting the elements in } A \times B \end{aligned}\)
Therefore, \(2 \cdot 0 = 0\)
Example 4
Use the set theory definition of multiplication to show that \(4 \cdot 3 = 12\)
Solution
Let A = {e, f, g, h} and B = {g, h, i }. Since n(A) = 4 and n(B) = 3, then
\( \begin{aligned} 4 \cdot 3 && = n(A) \cdot n(B) && \text{ by substituting n(A)for 2 and n(B)for 0} \\
&& = n(A \times B) && \text{ by the set theory definition of multiplication} \\
&& = n(\{(e, g), (e, h), (e, i), (f, g), (f, h), (f, i), (g, g), (g, h), (g, i), (h, g), (h, h), (h, i) \}) && \text{ by computing } A \times B \\
&& = 12 && \text{ by counting the elements in } A \times B \end{aligned}\)
Therefore, \(4 \cdot 3 = 12\)
Exercise 24
Use the set theory definition of multiplication to verify each multiplication. Show and justify each step. Only the solution to 24a is shown in the solutions.
a. \(5 \cdot 2 = 10\)
b. \(3 \cdot 1 = 10\)
c. \(0 \cdot 2\)
Here's a more geometrical approach to defining multiplication of two whole numbers.
Definition
To find the product of any two whole numbers, m and n, make a rectangular array of objects having m rows and n columns. The product of m and n, written \(m \times n\), equals the number of objects in the array.
The cool thing about using this geometrical approach is that any objects can be used, and one only needs to be able to count to get the answer. You don't need to use addition in order to multiply! I personally advocate having lots of graph paper around for anyone just learning to multiply. To compute \(4 \times 7\), you or the learner can mark off a rectangle on the graph paper that has 4 rows and 7 columns of boxes. The number of boxes in the rectangle is the answer to the problem. This is a useful tool for first learning a particular multiplication fact, or for anyone (adults, too) who forgot a fact and needs to figure it out again. The "objects" used on a graph paper are the individual boxes on the graph paper.
Here is how six different students might geometrically show how to multiply \(4 \times 7\).
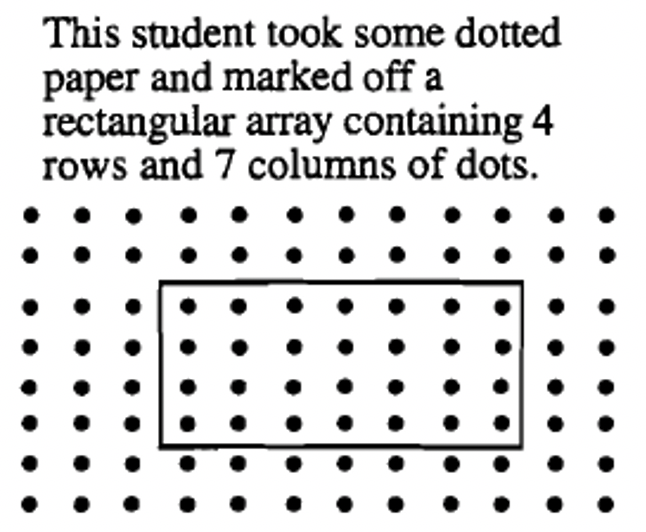 |
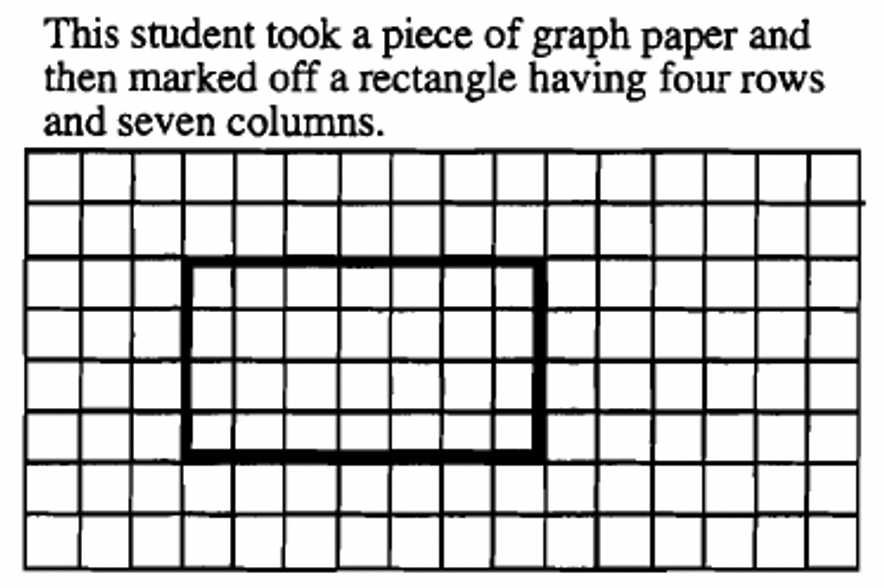 |
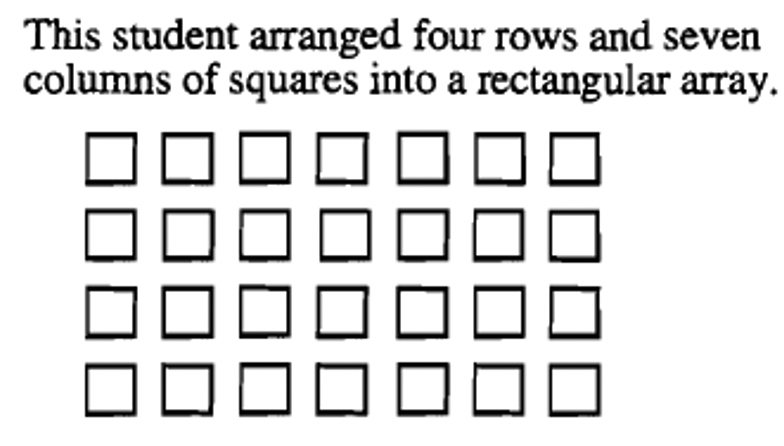 |
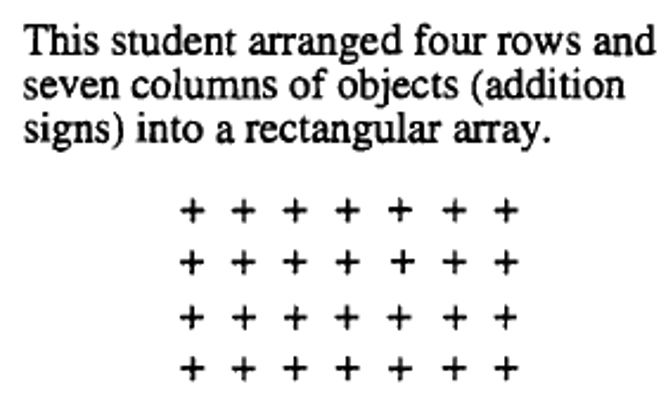 |
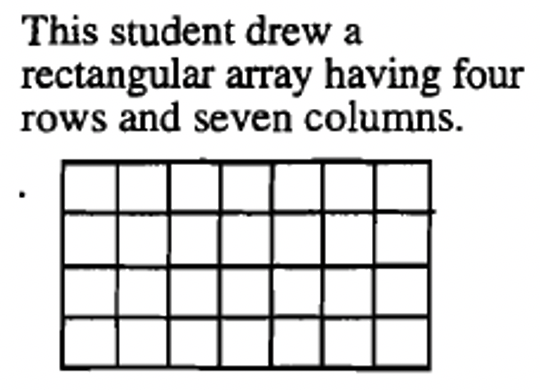 |
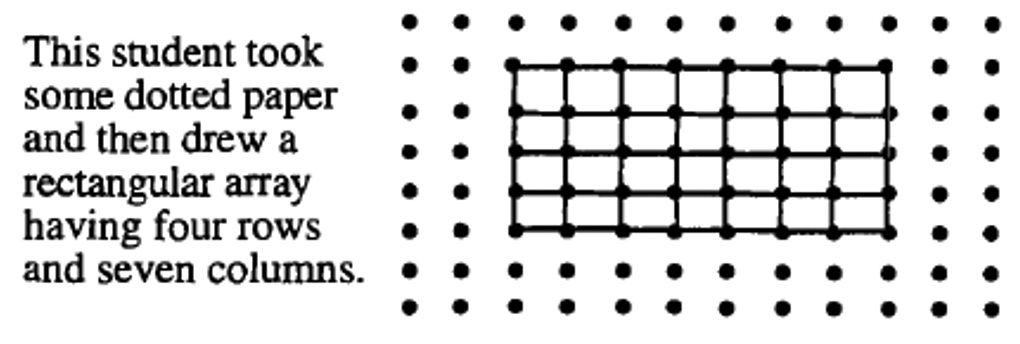 |
There is no point to making anyone stress out if they forgot, didn't memorize or couldn't recall the answer to \(4 \times 7\). The point is to KNOW WHAT MULTIPLICATION MEANS so you can figure a problem out again if you have to. Of course, there is merit to using flashcards and eventually memorizing basic multiplication facts like your multiplication tables. If not, it takes longer to do problems, you aren't able to focus on more advanced issues, and you might not trust your own mind. You shouldn't have to think about multiplication every time you have to multiply two numbers together, but you should be able to think about it. Knowing how to get the answer is better than having memorized a bunch of facts if you don't know where they came from, what multiplication really means, or how to figure it out again in case you forget the answer to some fact. And, as far as I'm concerned, nothing's wrong with using your fingers, either! Let people do what is comfortable for them, if they understand and can get the right answer, that's GREAT!
Exercise 25
Write the multiplication problem represented by each geometrical representation:
|
a. ____ 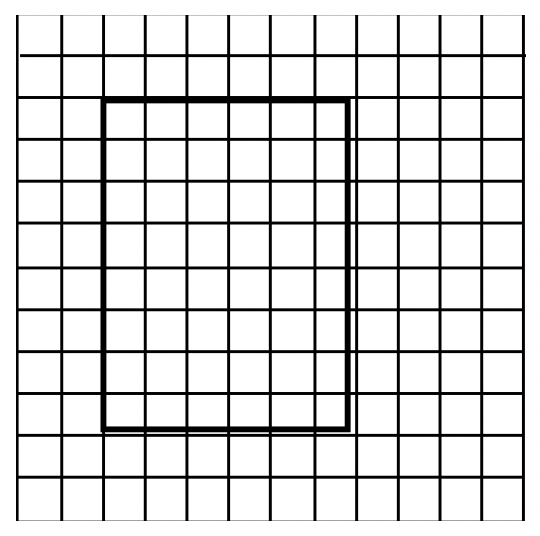 |
b. ____  |
|
c. ____ \(%\begin{matrix} \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \end{matrix}\nonumber\)  |
d. ____  |
|
e. ____  |
f. ____  |
Exercise 26
Show two different geometrical representations for \(4 \times 3\)
Exercise 27
For each multiplication, do the following to represent the multiplication: For part a, draw a rectangular array of objects, for part b use the graph paper, and for part c use the dotted paper. There are two ways you can choose to use the dotted paper.
|
a. \(2 \times 6\)
|
|
|
b. \(5 \times 3\)
|
|
|
c. \(3 \times 7\)
|
Exercise 28
a. Draw a rectangular array of boxes (a rectangle) on the graph paper provided to do the multiplication \(4 \times 6\):

b. Turn your page sideways and look at the rectangle. Draw what the picture looks like:

c. What multiplication problem is now represented? ________________
Exercise 28 should convince you that multiplication is commutative. In fact, the commutative property of multiplication is easiest to see using the geometrical approach. A rectangular array of objects having m rows and n columns represents the multiplication \(m \times n\). Once the rectangle is rotated \(90^{\circ}\) (or looked at sideways), there are now n rows and m columns, which represents the multiplication \(n \times m\). But of course, it's really the same rectangle of objects, so the number of objects in \(m \times n\) equals the number of objects in \(n \times m\). Therefore, \(m \times n = n \times m\). Okay, just for fun, one more time:
The commutative property of multiplication for whole numbers states that if a and b are any two numbers, then \(a \times b = b \times a\).
Wow! Isn't this exciting? There are several ways to think about and define multiplication, and we can show the commutative property still holds each time. Does it get any better than this? Well,...YES...but that's another story.
It's a little bit trickier to show on a two-dimensional page that the associative property of multiplication holds. With your work with the C-strips, you know multiplication is associative. Here's one way to geometrically model the multiplication of three numbers.
Definition
To find the product of any three whole numbers, \((a \times b) \times c\), first make a rectangular array of cubes (dice, sugar cubes, etc.) having a rows and b columns. Then, fill in c layers of the bottom rectangle to obtain a rectangular box, where the base of the box has width a and length b, and the height of the box is c.
Basically, you need to make (or visualize) a 3-dimensional box to do multiplication on three numbers. As it turns out, no matter how you construct it, if at the end, one dimension is a, one is b and the other is c, you've got the same box, and it holds the same number of cubes in it. Therefore, multiplication is associative. We won't be going through the motions of showing it in 3-dimensions, but elementary school children should have the benefit of working through it with cubes. I hope you'll model it this way if you become an elementary school teacher.
Since multiplication is both commutative and associative, any time more than two numbers are being multiplied together, the parentheses do not have to be shown, and the numbers can be multiplied together in any order.
For instance, notice how differently one might compute \(4 \times 10 \times 3 \times 5\)
Student 1: This person just goes left to right. First, \(4 \times 10\) is 40, then \(40 \times 3\) is 120, then \(120 \times 5 = 600\).
Student 2: This person first multiplies \(4 \times 5\) to get 20, then multiplies \(10 \times 3\) to get 30, then multiplies the two answers together, \(20 \times 30\) to get 600.
Student 3: This person does \(4 \times 5\) first to get 20, then multiplies by 3 to get 60, then multiplies by 10 to get 600.
Student 4: This person multiplies \(3 \times 5\) first to get 15, then multiplies that by 4 to get 60, and then multiplies by 10 to get 600.
And there are many more possibilities. The point is that you have the option of multiplying in any order and any combination you want. The following show how this is very convenient for certain computations:
Example
\(5 \times 87 \times 2\): Well, it's easier to multiply the 5 and 2 first to get 10 and then multiply by 87 to get 870. Otherwise, you could do \(5 \times 87\), which isn't so easy to do in your head.
Example
\(8 \times 22 \times 5\): Well, I'd do 8 times 5 first to get 40 and then multiply by 22 to get 880.
Exercise 29
Make up a multiplication problem, where it would be easier to multiply by doing some rearranging first. Explain your steps and how to get the answer.
Exercise 30
We're going to show that \(3 \times (4 + 2) = (3 \times 4) + (3 \times 2)\). Let's first work on the right side of the equation, which has two parts.
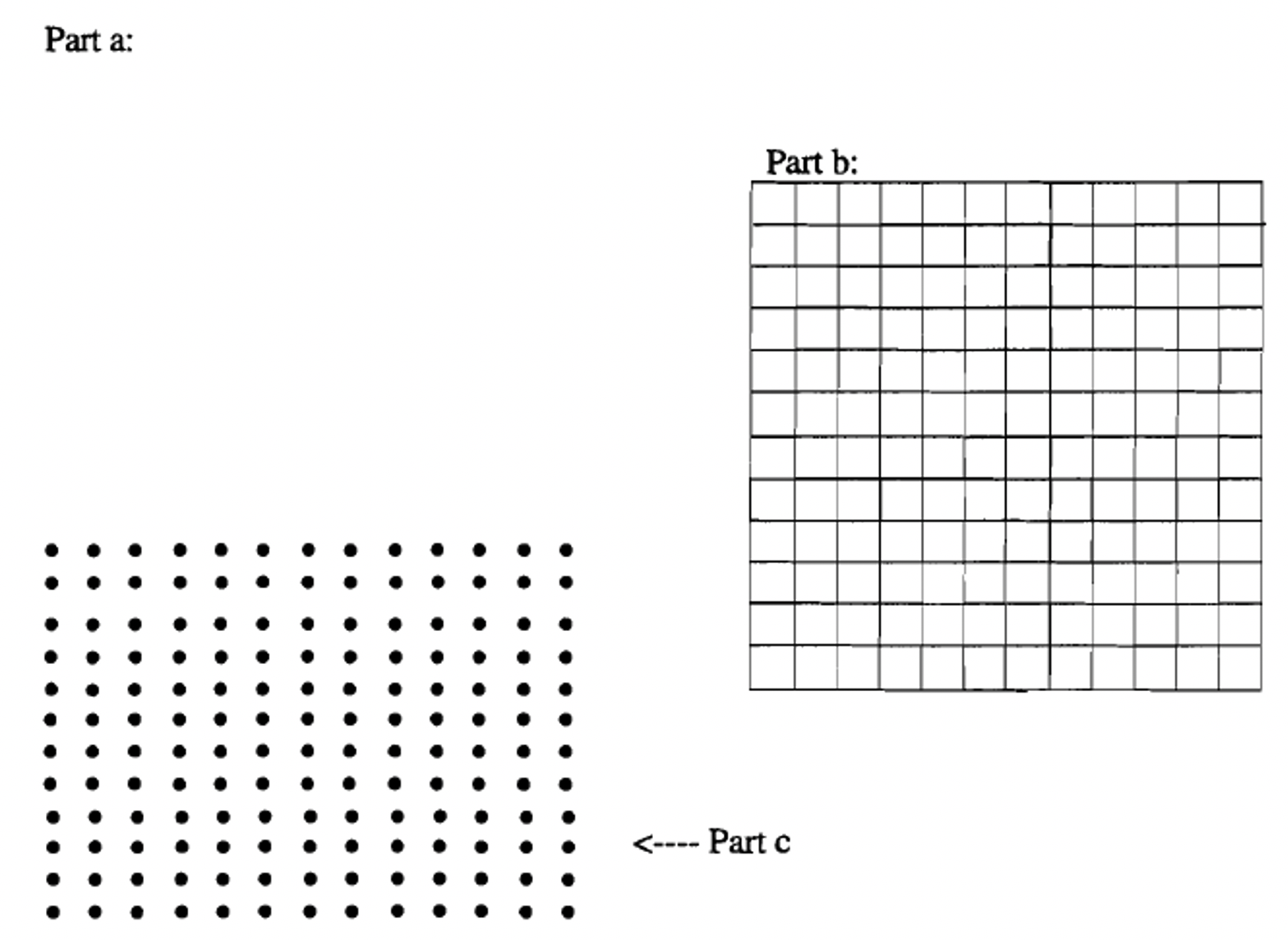
a. Draw a rectangular array of dots or stars to represent \(3 \times 4\).
b. Now, draw a rectangular array of dots or stars to represent \(3 \times 2\).
c. Since the right side of the equation says to join the two parts together (addition), then draw the array from part a below, and right next to it, draw the array from part b.
d. Now, let's do the left hand side of the equation, \(3 \times (4 + 2)\). We first have to compute in the parentheses to get \(3 \times 6\). So, make a rectangular array of dots or stars to represent \(3 \times 6\).
e. Is the number of dots or starts in part c equal to the number of dots or starts in part d?
Exercise 31
What property did you just illustrate in exercise 30?
Well, I hope you realize you just showed that multiplication distributes over addition. In fact, it is also true that multiplication distributes over subtraction. In other words,
For any three whole numbers, a, b and c, where b > c, \(a \times (b + c) = (a \times b) + (a \times c)\) and \(a \times (b – c) = (a \times b) – (a \times c)\).
Exercise 32
Show that \(2 \times (3 + 4) = (2 \times 3) + (2 \times 4)\) using a geometrical approach, like you did in exercise 30. Explain the steps.
Exercise 33
a. Form the train \(P \times (Y – L)\) by first forming the train Y – L. Find out what C-strip Y – L is. Then do the multiplication \(P \times (Y – L)\). Exactly how many white C-strips make up this train?
b. Form the train \(P \times Y\) and \(P \times L\). Now subtract the second train from the first train. Exactly how many white C-strips make up this train?
c. Compare the lengths of the trains from part a and b.
Exercise 33 showed that \(P \times (Y – L) = P \times Y – P \times L\). This is one illustration that multiplication distributes over subtraction.