5.2: Multiplication Algorithms
- Last updated
- Save as PDF
- Page ID
- 83003
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)You will need: Base Blocks (Material Cards 4-15)
There are many algorithms for multiplication. Personally, I think the way most of us learned it in school is one of the hardest algorithms. It's an uphill battle getting new methods into the school system. But, it's worth pursuing. It's a good thing to know what multiplication means, and how to multiply any two numbers together. However, there is no reason that everyone should have to use the same method to obtain the answer. In this exercise set, you'll learn some new algorithms for multiplication. You'll also learn how to multiply in different bases.
Many people use repeated addition all the time to multiply. Consider the multiplication problem 26 times 17. Basically, this means add 26 seventeens added together. This could be done by adding them together one at a time. That would take a long time.
Another approach would be to add 10 seventeens together first to get 170, then add 10 more seventeens together to get 170 again, then add 5 more seventeens together which is 85, and then add one more seventeen. Adding 10 seventeens (170), 10 seventeens (170), 5 seventeens (85) and 1 seventeen (17) gives 170 + 170 + 85 + 17 = 442, which is exactly the answer to 26 times 17. That should be no surprise since we added 26 (10+10+5+1) seventeens together.
Someone else might add 10 seventeens (170), 10 seventeens (170), 3 seventeens (51) and 3 more seventeens (51) to get 170 + 170 + 51 + 51 = 340 + 102 =442.
There are several other ways people might break up the number 26 and still get the correct answer. This approach may be one you frequently or maybe this is the first time you've thought of it this way. In any case, it's different from just doing it the same old way.
Because of the commutative property, you could have done 17 times 26 instead. Maybe you'd add 10 twenty-sixes (260), then 5 more twenty-sixes (130) and 2 more twenty-sixes (52) to get 260 + 130 + 52 = 442.
One reason it's advantageous to do multiplication using repeated addition is that many problems can be done in your head this way. But, of course, every new method takes practice and getting used to, and it's common for people to revert back to using their old, familiar methods even if it takes longer and requires paper. That's okay, too. It is, however, very important that a teacher knows several ways so that he or she can provide more opportunities for students. What seems obvious to one student is foreign to another, so you give alternatives and present different ways of looking at things.
Exercise 1
Use some form of repeated addition to do the following multiplications. Explain how you do each one.
a. \(23 \times 13\)
b. \(14 \times 14\)
One new algorithm (for most of you reading this) is called Duplation. This is actually a very old algorithm used in ancient times by the Egyptians. It also uses the principle that multiplication is simply repeated addition. It is called duplation because it uses the idea of doubling numbers to get the answer. Let's look again at the first multiplication we did in this section. It was \(26 \times 17\). Since 26 seventeens must be added together, the number 26 is broken down into powers of two. It's easy to get powers of two: simply start with 1, then double it to get 2, then double it to get 4, then double it to get 8, then double it to get 16, etc. To figure out how far you have to go in the doubling process, stop if doubling gives a number bigger than the number you are trying to break down (26, in this case). Now, all this sounds more complicated than it really is. Before explaining too much more, notice how you'll write it. Write 26 at the top and underline it. Underneath, start with 1, then, double continuously, stopping at 16 since if you doubled another time, you'd get a number bigger than 26. To the right of 26, write the number 17 and underline it.
Underneath it, first write 17, then double 17 to get 34, then double 34 to get 68, double 68 to get 136, etc., until you have the same amount of numbers under the 17 as you do under the 26.
\(\begin{aligned} &\begin{matrix}\underline{26} && \times & \underline{17} \\ 1 && 17 \\ 2 && 34 \\ 4 && 68 \\ 8 && 136 \\ 16 && 272 \end{matrix} \\ &\begin{matrix} \cdots \cdots && \cdots \cdots \end{matrix} \end{aligned}\)
Do you see the corresponding numbers? 1 corresponds with 17, because 17 is \(1 \times 17\), 2 corresponds with 34, because 34 is \(2 \times 17\), 4 corresponds with 68, because 68 is \(4 \times 17\), 8 corresponds with 136, because 136 is \(8 \times 17\), and 16 corresponds with 272, because 272 is \(8 \times 17\). Now, you may need to think about this for a few minutes. The left side keeps track of how many of some number you are adding together. So, the \(1 \times 17\) should be clear. So, \(2 \times 17\) is simply 17 doubled. Now if \(2 \times 17\) is 34, then \(4 \times 17\) is twice as many as \(2 \times 17\), so double 34 to get 68. This continues on and on. So, if \(8 \times 17\) is 136, then if we double 136, we should have \(16 \times 17\). Isn't it neat how we know that \(16 \times 17 = 272\) and we just double a few numbers to get there?
Okay, now we only need to add 26 seventeens together. Simply start at the bottom of the first column, and check off numbers that add up to 26 (this is like doing it in base two). After you check off the numbers in the left column, circle or point to their corresponding numbers in the right column. It's those numbers in the right column that you add together to get the answer. Watch how the rest of the problem is done:
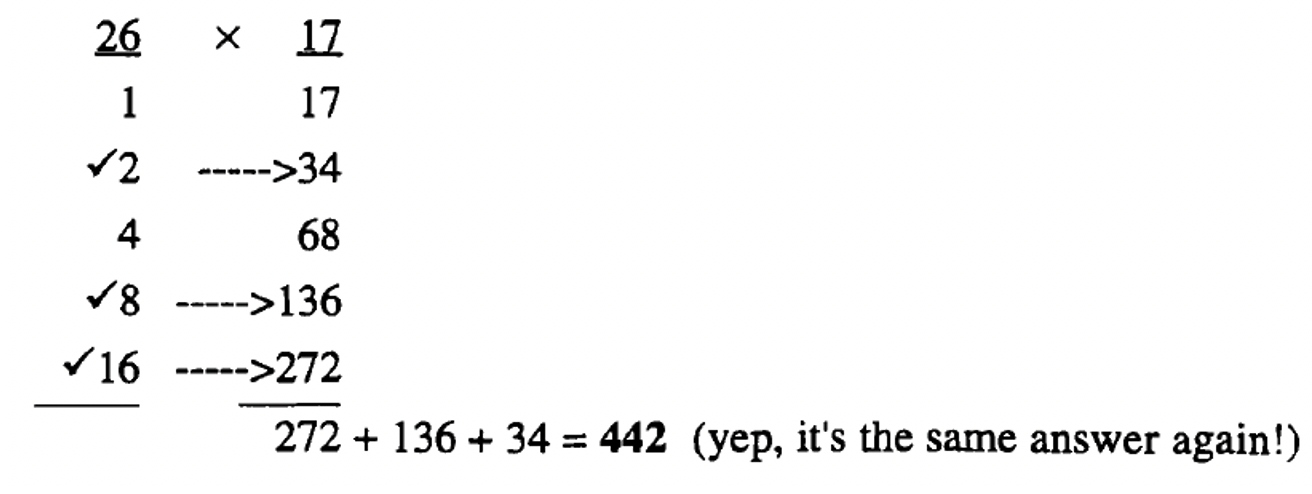
Let's do the same problem over again, but use the commutative property of multiplication. In other words, use the duplation method to compute: \(17 \times 26\). This time, in the left column, you check off numbers that add up to 17 it's coincidental that I had to double to 16 again and stop. In the right hand column, start with 26 and double away.

Here are two more examples for you to study. I'll do \(15 \times 35\) and \(35 \times 15\).

Of course, because of the commutative property of multiplication, the answer is 525, no matter which way you do it. Are you ready to try a couple of duplation problems of your own? Well, ready or not, here they come!
Exercise 2
Multiply \(13 \times 29\) using duplation. Then, multiply \(29 \times 13\) using duplation. Show all of your work. Make it clear what is added together for each problem.
Exercise 3
Use duplation to multiply 27 by 14, and then 14 by 27. Show your work.
Here is an example of how the Egyptians multiplied using duplation.
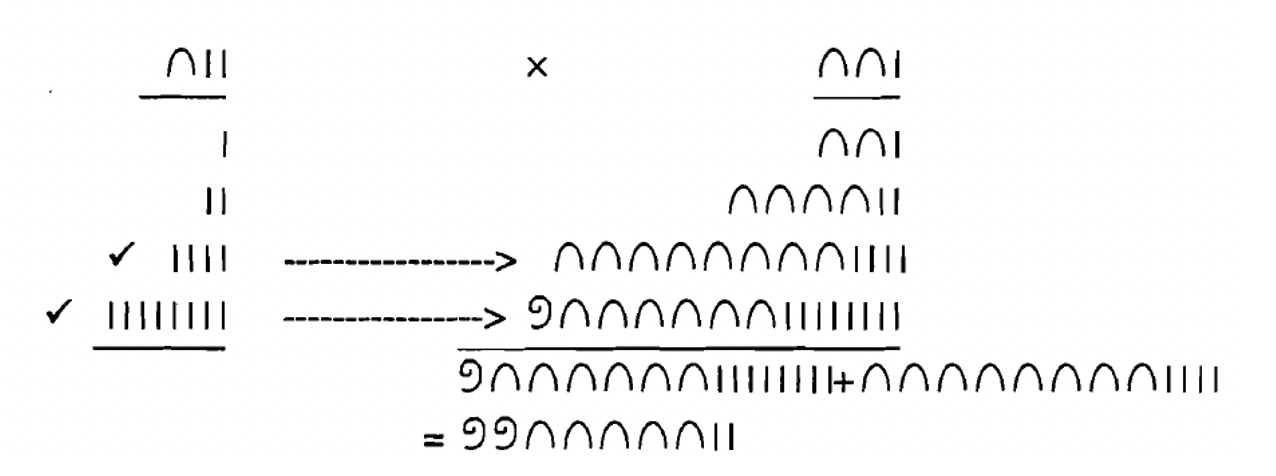
Exercise 4
Use duplation to multiply 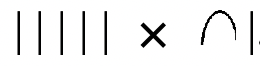 .
.
Do the problem entirely in Egyptian.
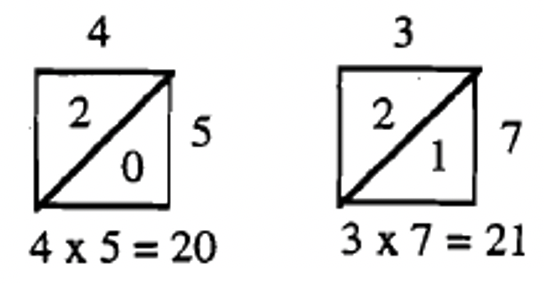
You are going to learn a cool and easy way to multiply numbers together. But first, I’ll show you how to multiply 2 single digits together. Make a square with a diagonal in it. Put one number on top and the other on the right of the square. Multiply the two digits together and put the answer in the box with the diagonal. Look at the examples to the right.
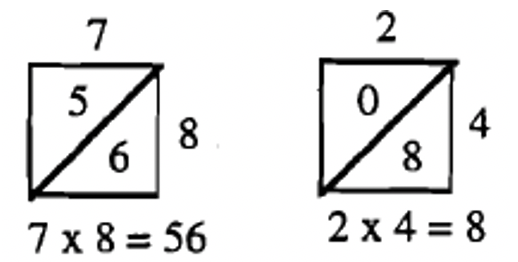
The method you are now going to learn is called the LATTICE METHOD and it could be used for multiplying 2 digit or 3 digit or even bigger numbers together. The example well do is \(47 \times 32\).
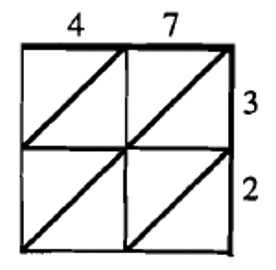
STEP 1: To begin, put one of the numbers at the top (47) of a rectangle (that has a space for each digit in the number) and the other number along the side (32) of the same rectangle (that has a space for each digit). In this case, we need a rectangle that has two spaces across the top and 2 spaces along the side. Then, you make diagonals. Look to the right.
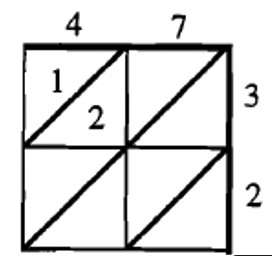
STEP 2: Multiply each of the digits on the top by each of the digits along the side, and put the answer where they would meet. For instance, look where the 12 goes when you multiply 4 times 3.
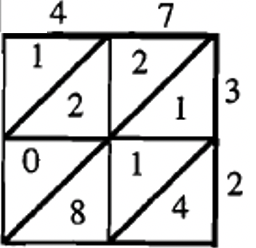
STEP 3: There are three other multiplications to do: 7 times 3, 4 times 2 and 7 times 2. Do you see how all the answers are filled in? It doesn’t matter which ones you multiply and put in first.
STEP 4: There are four diagonals (made up of little triangles) slanting to the right inside the rectangle. Starting with the one in the right bottom corner, add the digits inside each diagonal and fill put the sum in the “cup” under its diagonal. In the first diagonal is 4, so 4 is put in the “cup” under its diagonal (bottom right of rectangle). In the next diagonal are three digits a 1, 1 and 8 which adds up to 10, so put a 0 in the cup under that diagonal (at the bottom to the left) and a 1 (for the carry) in one of the triangles to the left. The next diagonal has a 2, 2, 0 and 1, which adds up to 5, and goes in the “cup” under its diagonal (left, bottom). In the last diagonal, there is just a 1, so a 1 is put in the “cup”under its diagonal (left, top). Look at how I filled in the numbers one at a time.
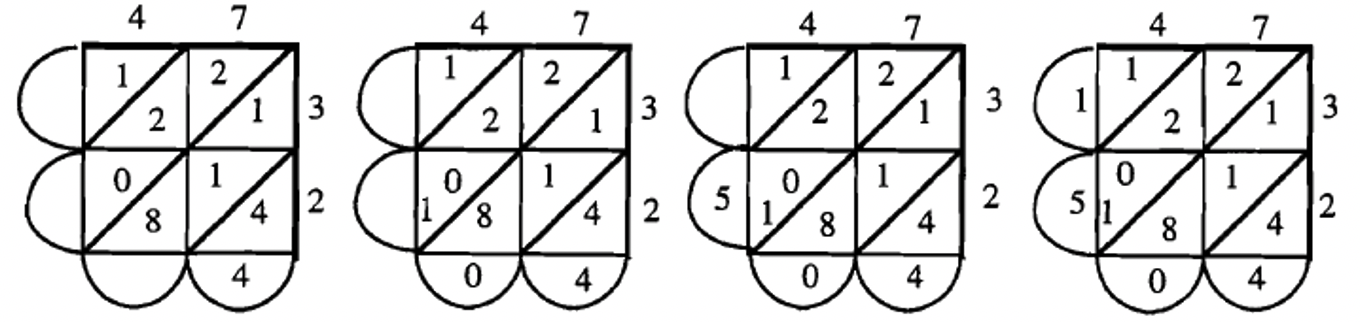
STEP 5: The numbers you filled in under each diagonal in the “cups” (outside the rectangle) form the answer. It is read by starting at the left top and reading down and then across the bottom. In this case, the answer is 1504. Isn’t that cool? That’s all there is to it!
Most of my students love this very old Lattice method of multiplying. It works as easily for small numbers as it does for large numbers. First, you simply do a series of simple single digit multiplications, and then you add, with carrying. Actually you could use the left to right (with underlining for carrying) method of addition for the last step. The main disadvantage is that you have to draw a lattice, which is a small price to pay to make multiplication easier and less complicated. Most likely, it takes less time than using the standard algorithm with carrying, because there's less chance of error and confusion with all that multiplying and carrying, etc. I propose all students learn multiplication this way first, and let them stay with it if they like it. Who needs to shorten it up and make it more complicated than it really is? Ah, well, I take it you get my point.
Exercise 5
Use the lattices provided in a - d to multiply the given numbers. Then write the answer in the space provided. For e, draw your own lattice to compute the multiplication. By the way, you don't have to draw the little cups. That was my own little invention so it would be easy to identify the answer. There are two more problems (f and g) on the next page. Check your answers with a calculator
|
a. \(63 \times 57\) = ____  |
b. \(342 \times 85\) = ____  |
|
c. Make up a problem:  |
d. Make up a problem:  |
| e. \(58 \times 67\) = ____ Draw your own lattice. |
Exercise 6
a. Get out your Base Four Blocks. Take 41 units, and trade them in using your Base Four blocks. You should have some flats, longs and units which you can write as a numeral in Base Four.
Write the Base Four numeral here:
b. If you wanted to multiply 2 times that number, you would need to make two piles representing that number, join the two equal piles together (since multiplication is repeated addition) and then take the new pile and make trade-ins. Make two equal piles with the blocks, where each pile is the same as the one you formed from trade-ins in part a.Draw a picture of what the two piles look like.
c. Join the two piles together and make trade-ins to get a new base four numeral. Write this Base Four numeral here:
d. Fill in the first blank with what you got for part a and the second blank with what you got for part c. You just did a multiplication problem in Base Four using repeated addition!
\(2_{\text{four}} \times\) _____ \(_{\text{four}} = \) _____ \(_{\text{four}}\)
Exercise 7
a. Write the Base Four numeral from 6a here:
b. If you wanted to multiply 3 times that number, you would need to make three piles representing that number, join the three equal piles together (since multiplication is repeated addition) and then take the new pile and make trade ins. Make three equal piles with the blocks, where each pile is the same as the one you formed from trade-ins in part a. Draw a picture of what the three piles look like.
c. Join the three piles together and make trade-ins to get a new base four numeral. What Base Four numeral did you get?
d. Fill in the first blank with what you got for part a and the second blank with what you got for part c. You just did another multiplication problem in Base Four using repeated addition!
\(3_{\text{four}} \times\) _______ \(_{\text{four}} =\) _____ \(_{\text{four}}\)
Exercise 8
Using the same procedure as in 6 and 7, take out your base three blocks and do the following multiplication: \(2_{\text{three}} \times 221_{\text{three}}\). Explain your work, and show pictures.
Exercise 9
If you wanted to do \(10_{\text{three}} \times 221_{\text{three}}\), you would need to trade the long (\(10_{\text{three}}\)) in for three units, make three piles using Base three blocks representing \(221_{\text{three}}\), and do the same thing you did in exercise 7. Explain how you do this and show pictures.
This method of repeated addition with the blocks would be too cumbersome if we were working with higher numbers. For instance, if you were trying to use this method to multiply \(321_{\text{four}} \times 312_{\text{four}}\), the first number when broken down into single units would consist of more than 50 units, and that would be way too many piles to make! Instead, we'll think about and figure out what it means to multiply using larger blocks than units. For instance, we'll figure out what a flat times a long is, or what a long times a flat is in any base! We'll be using these abbreviations: U for unit, L for long, F for flat, B for block, LB for long block, FB for flat block, and BB for block block.
Exercise 10
a. Get out your base three blocks. You're going to find the product of a long and a long similar to how you did products with the C-strips in Exercise Set 1. \(L \times L\) is obtained by putting one long in the horizontal position and the second long in the vertical position, underneath and perpendicular to the first long. Then form a rectangle of longs underneath. Take the rectangle (don't include the top horizontal long) and trade up in base three, if possible. What is the product of long and a long in base three?
b. Get out your base four blocks. Find the product of long and a long in base four using the method explained in part a. What is the product of long and a long in base four?
c. Get out your base five blocks. Find the product of long and a long in base five using the method explained in part a. What is the product of long and a long in base five?
d. In any base, what is the product of a long and a long? \(L \times L =\)
Exercise 11
a. Get out your base three blocks. You're going to find the product of a flat and a long now. First, we need to convert the flat to longs so that we can make a horizontal train across the top of the T. Do this. Then, put a long in the vertical position, underneath and perpendicular to the long train of longs making the top of the T. Then form a rectangle of longs underneath. Take the rectangle (don't include any longs from the top horizontal part of the T) and trade up in base three, if possible. What is the product of flat and a long in base three?
b. Get out your base four blocks. Find the product of flat and a long in base four using the method explained in part a. What is the product of flat and a long in base four?
c. Get out your base six blocks. Find the product of flat and a long in base six using the method explained in part a. What is the product of flat and a long in base six?
d. In any base, what is the product of a flat and a long? \(F \times L =\)
Exercise 12
a. Get out your base three blocks. You're going to find the product of a block and a long now. First, we need to convert the block to flats, and then the flat to longs so that we can make a horizontal train across the top of the T. Do this. Then, put a long in the vertical position, underneath and perpendicular to the long train of longs making the top of the T. Then form a rectangle of longs underneath. Take the rectangle (don't include any longs from the top horizontal part of the T) and trade up in base three, if possible. What is the product of block and a long in base three?
b. Get out your base four blocks. Find the product of block and a long in base four using the method explained in part a. What is the product of block and a long in base four?
c. Get out your base two blocks. Find the product of block and a long in base two using the method explained in part a. What is the product of block and a long in base two?
d. In any base, what is the product of a block and a long? \(B \times L =\)
Exercise 13
Summarize the results from part d of exercises 10, 11 and 12.
a. \(L \times L =\) _______
b. \(L \times F =\) _______
c. \(L \times B =\) ________
Use the commutative property of multiplication to compute the following:
d. \(F \times L =\) ________
e. \(B \times L =\) ________
Exercise 14
In your own words, what happens when something is multiplied by a long?
Did you notice that when something is multiplied by a long, it bumps up to the next place value. This is analogous to multiplying by 10 in base 10, since 10 is a long in base ten. For instance, in base 10, 347 represents 3 hundreds, 4 tens and 7 ones; when you multiply \(347 \times 10\), you get 3470, 3 thousands, 4 hundreds and 7 tens, the place value for each digit moved up one place value.
Exercise 15
Consider multiplying \(312_{\text{four}} \times 10_{\text{four}}\). This means you are multiplying a number in base four by a long in base four. Get out your base four blocks and represent the number \(312_{\text{four}}\).
a. You have ____ flats, _____ longs and _____ units.
b. If you multiply each of these by the long, now how many of each type of place value block do you have in base four?
To multiply a two-digit numeral, X, in a base by some number, Y, in that base, the idea of repeated addition can be used. For instance, if we represent the number with base blocks, we'll want to create an "answer pile" where we put the blocks representing the product as we multiply by the two-digit numeral. Every unit in X multiplied by Y gives us one set of base blocks contained in Y in the answer pile. Every long in X multiplied by Y gives us the next place value up for each of the base blocks contained in Y. This is much more complicated to explain than to do with the blocks. So, let's do an example.
Get out your Base Four Blocks. We'll multiply \(23_{\text{four}} \times 32_{\text{four}}\). With your blocks, represent this as a multiplication problem. It should look something like this:

Recall that each long in the bottom multiplied by the top makes each top piece move up to the next higher place value block. So, when the first bottom long is multiplied by the top number, 2 flats and 3 longs go into the answer pile. When the second bottom long is multiplied by the top number, another 2 flats and 3 longs go into the answer pile. When the third bottom long is multiplied by the top number, yet another 2 flats and 3 longs go into the answer pile. When I do this with the blocks, I usually move each part of the multiplier (bottom number) I've done so far to the right or out of the way. In any case, in your answer pile, you should now have 6 flats and 9 longs in the answer pile. We still have to multiply by each of the two units. Each unit multiplied by the top number gives a set of the top number; it's like multiplying by 1. So, when the first bottom unit is multiplied by the top number, 2 longs and 3 units go into the answer pile. When the second bottom unit is multiplied by the top number, another 2 longs and 3 units go into the answer pile. Create a place for the answer pile and do this with your blocks. Try it yourself, then check on the next page.
I'll show the answer pile below: each row shows what I got as I multiplied each bottom piece (3 longs and 2 units) by the top. By the way, you could have multiplied by the units first and then by the longs I'll do it that way for the next example. It all just eventually ends up in the answer pile and all exchanges have to made in the end, so you can write it in Base Four. This is \(23_{\text{four}} \times 32_{\text{four}}\):

THE Answer PILE IS SHOWN BELOW:
Now, make all your trade-ins with these pieces. You should end up with 2 blocks, 1 flat, 2 longs and 2 units, which is the number \(2122_{\text{four}}\), written in base four.
Next, we'll multiply \(132_{\text{four}} \times 23_{\text{four}}\). With your blocks, represent this as a multiplication problem. It should look something like this:

Each unit multiplied by the top number gives a set of the top number it's like multiplying by 1. So, when the first bottom unit is multiplied by the top number, a flat, 3 longs and 2 units go into the answer pile. When the second bottom unit is multiplied by the top number, another flat, 3 longs and 2 units go into the answer pile. When the third bottom unit is multiplied by the top number, yet another flat, 3 longs and 2 units go into the answer pile. Create a place for the answer pile and do this with your blocks. When I do this with the blocks, I usually move each part of the multiplier I've done so far to the right or out of the way. In any case, in your answer pile, you should now have 3 flats, 9 longs and 6 units in the answer pile. We still have to multiply by each of the two longs. Recall that each long multiplied by the top makes each top piece move up to the next higher place value block. So, when the first bottom long is multiplied by the top number, a block, 3 flats and 2 longs go into the answer pile. When the second bottom long is multiplied by the top number, another block, 3 flats and 2 longs go into the answer pile. I'll show the answer pile below: each row shows what I got as I multiplied each bottom piece (3 units and 2 longs) by the top. By the way, you could have multiplied by the longs first and then by the units. It all just eventually ends up in the answer pile and all exchanges have to made in the end, so you can write it in Base Four. This is \(132_{\text{four}} \times 23_{\text{four}}\):

THE Answer PILE IS SHOWN BELOW:
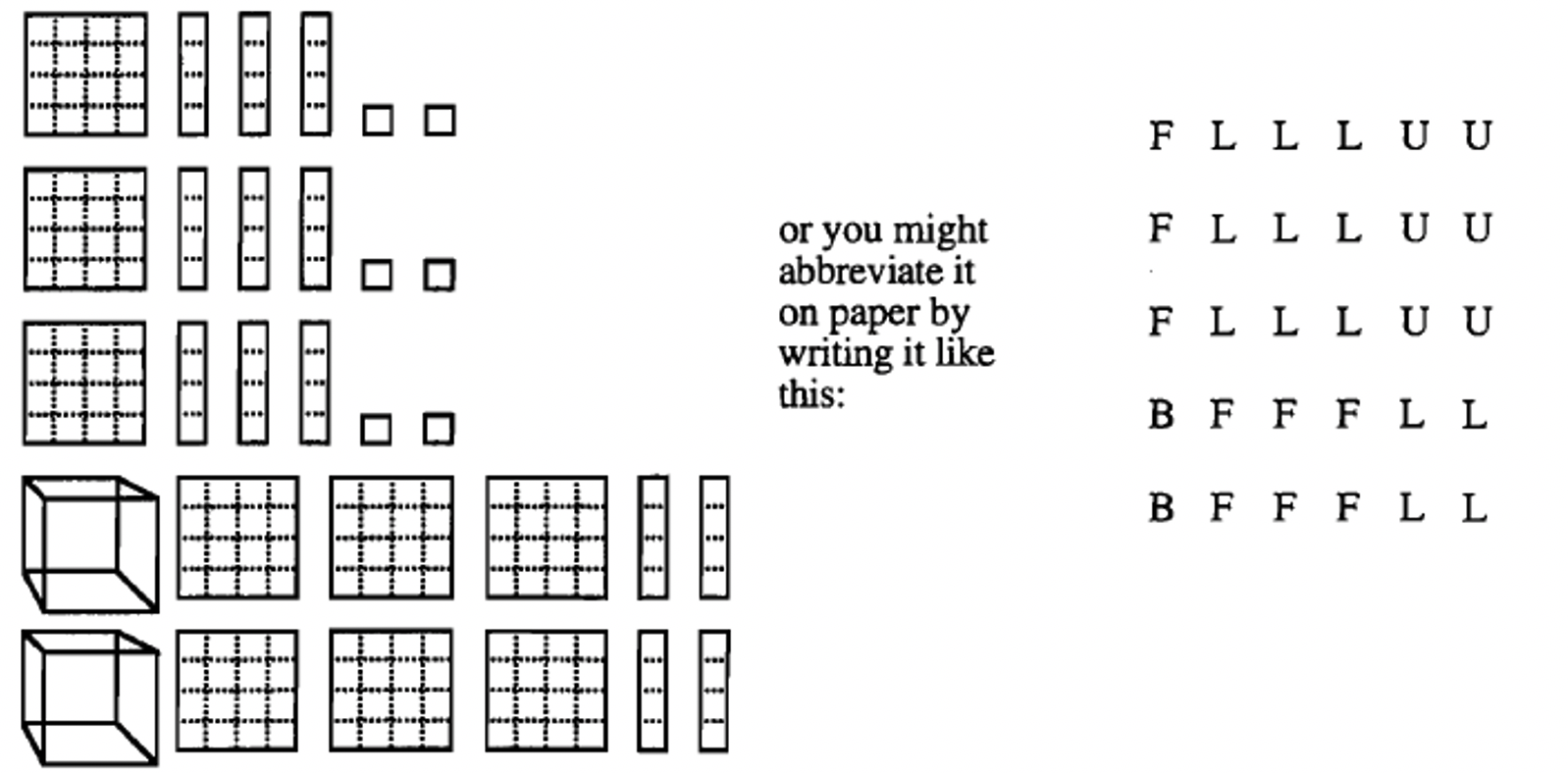
Now, make all your trade-ins with these pieces. You should end up with 1 long block, 1 block, 2 longs and 2 units, which is the number \(11022_{\text{four}}\), written in base four. Make sure you do and understand these last two problems before going on.
Exercise 16
Multiply each of the following using base blocks. Then explain and draw the steps in the space below as done in the previous two examples.
a. Use Base Four blocks to multiply \(12_{\text{four}} \times 31_{\text{four}}\)
b. Use Base Three blocks to multiply \(112_{\text{three}} \times 21_{\text{three}}\)
Exercise 17
a. Get out your base three blocks. You're going to find the product of a flat and a flat now. We need to convert the first flat to longs, make a train, and put this horizontal train across the top of the T. Do this. Then, convert the second flat to longs, make a train, put this train in the vertical position, underneath and perpendicular to the long train of longs making the top of the T. Then form a rectangle of a bunch of longs underneath. Take the rectangle (don't include any longs from the top horizontal part of the T) and trade up as much as possible in base three, if possible. What is the product of flat and a flat in base three?
b. Here's another way to find the product of a flat and a flat in base three. For each unit in the first flat, put a flat in an answer pile. Take all those flats in the answer pile and trade them in to see what you get. What is the product of flat and a flat in base three?
c. Get out your base two blocks. Find the product of flat and a flat in base two using the method explained in part a or b. What is the product of flat and a flat in base two?
d. Complete the following: In any base, \(F \times F =\) _____
Another way to think about what happens when you multiply by a flat is to think of a flat as a long times a long. Let's say you are multiplying something by a flat. First, multiply it by a long, which means it moves up one place value, and then multiply that answer by a long once more, which means it moves up one more place value. So, anything multiplied by a long moves up one place value, and anything multiplied by a flat moves up two place values. Multiplying by a flat is analogous to multiplying by 100 in base ten. 100b in any base b represents a flat. Think about what happens when a block is multiplied by anything.
Exercise 18
Complete the following:
| a. \(U \times U =\) ____ | f. \(F \times U = \) _______ |
| b. \(U \times L = \) _____ | g. \(B \times U = \) _______ |
| c. \(U \times F = \) _____ | h. \(L \times L = \) _______ |
| d. \(U \times B = \) _____ | i. \(L \times F = \) _______ |
| e. \(L \times U = \) _____ | j. \(L \times B = \) _______ |
Exercise 19
Use base six blocks to multiply the following. \(105_{\text{six}} \times 123_{\text{six}}\). If you have trouble, go on to the next page, where it is explained and then try it again. Show the steps and diagram.
If you had trouble with #19, below is an abbreviated picture of of the steps. The multiplication shown on the left is \(105_{\text{six}} \times 123_{\text{six}}\) and the multiplication shown on the right is \(123_{\text{six}} \times 105_{\text{six}}\) In both cases, I started multiplying with the biggest block at the bottom and moved left to right. In both cases, the final result is the same, and after all exchanges have been made, there is 1 long block, 3 blocks, 4 flats and 3 units, which is \(13403_{\text{six}}\), written in base six. It takes a lot of practice to really do this with the blocks. But it's fun once you get it!
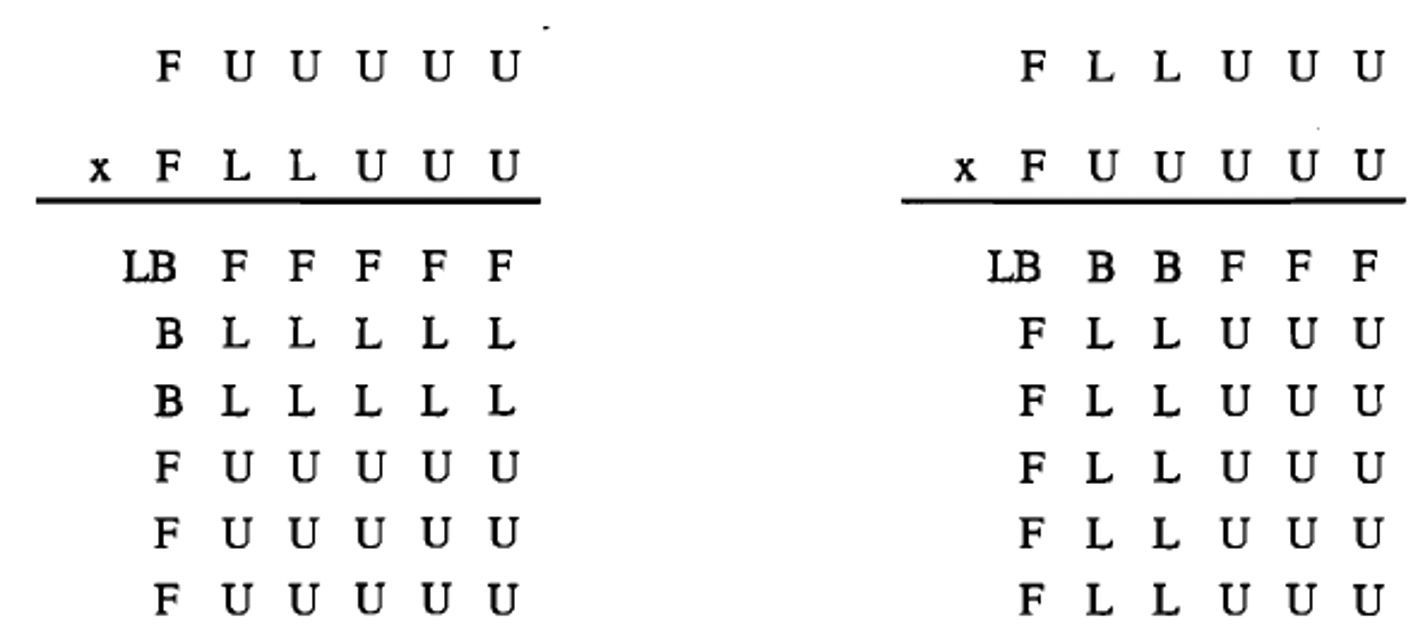
Exercise 20
Use base three blocks to multiply \(102_{\text{three}} \times 120_{\text{three}}\). Show steps like done in the example shown above.
We can shorten up this process of multiplying with the blocks even further. In exercise 18, you showed the products obtained when multiplying two base blocks together. The interesting thing is that a flat times a long is a block, no matter what base you are in. You can actually make up a multiplication chart for using blocks.
Exercise 21
Complete the rest of the multiplication chart below.
| \(\times\) | U | L | F | B |
| U | ||||
| L | L | B | ||
| F | FB | |||
| B | LB |
In our first example with the blocks, we computed \(23_{\text{four}} \times 32_{\text{four}}\). Since we are multiplying 2 longs and 3 units by 3 longs and 2 units, the multiplication can be written as \((2L + 3U) \times (3L + 2U)\). Applying the distributive property (or FOIL), we get
\((2L + 3U) \times (3L + 2U)\)
= \(2L \times 3L + 2L \times 2U + 3U \times 3L + 3U \times 2U\)
= \(\bf (2 \times 3)(L \times L) + (2 \times 2)(L \times U) + (3 \times 3)(L \times U) + (3 \times 2)(U \times U)\)
= 6F + 4L + 9L + 6U
= 6F + 13L + 6U **
At this point exchanges have to be made. In Base Four,
6F = 1B + 2F, 13L = 3F + 1L and 6U = 1L + 2U
= 1B + 2F + 3F + 1L + 1L + 2U
= 1B + 5F + 2L + 2U
The 5 flats are now exchanged for a block and a flat
= 1B + 1B + 1F + 2L + 2U
= 2B + 1F + 2L + 2U
which is written as \(2122_{\text{four}}\) in base four. This is the same answer we got before.
**If I were doing \(23 \times 32\) in a different base, all of steps up to this point are exactly the same. For instance, on the next page, the same basic problem is done in base six. All of the steps are the same, but notice that once exchanges are made, they are done with base six blocks in mind.
Also, it isn't necessary to write out the step that is in bold type. That's an application of the commutative and associative properties, and I wanted to show that step for clarification.
Here is the same basic problem done in Base Six.
\( \begin{aligned} & 23_{\text{six}} \times 32_{\text{six}} = (2L + 3U) \times (3L + 2U) \\ &= 2L \times 3L + 2L \times 2U + 3U \times 3L + 3U \times 2U \\ &= (2 \times 3)(L \times L) + (2 \times 2)(L \times U) + (3 \times 3)(L \times U) + (3 \times 2)(U \times U) \\ &= 6F + 4L + 9L + 6U \\ &= 6F + 13L + 6U \\ &= 1B + 2F + 1L + 1L \\ &= 1B + 2F + 2L \\ &= 1220_{\text{six}} \end{aligned} \)
Here is the same basic problem done in Base Nine.
\( \begin{aligned} & 23_{\text{nine}} \times 32_{\text{nine}} = (2L + 3U) \times (3L + 2U) \\ &= 2L \times 3L + 2L \times U 3U \times 3L + 3U \times 2U \\ &= 6F + 4L + 9L + 6U \\ &= 6F + 13L + 6U \\ &= 6F + 1F + 4L + 6U \\ &= 7F + 4L + 6U \\ &= 746_{\text{nine}} \end{aligned}\)
Exercise 22
Show the steps using the blocks as shown in the previous examples to multiply the following.
a. \(23_{\text{five}} \times 32_{\text{five}}\)
b. \(42_{\text{eight}} \times 53_{\text{eight}}\)
Here is an example of using this method for numerals with more than two digits each. You still use the distributive property. Each term in the first parentheses is multiplied by each term in the second parentheses.
\(\begin{aligned} & 212_{\text{five}} \times 102_{\text{five}} = (2F + 1L + 2U) \times (1F + 2U) \\ &= 2F \times 1F + 2F \times 2U + 1L \times 1F + 1L \times 2U + 2U \times 1F + 2U \times 2U \\ &= 2LB + 4F + 1B + 2L + 2F + 4U \\ &= 2LB + 1B + 6F + 2L + 4U \\ &= 2LB + 1B + 1B + 1F + 2L + 4U \\ &= 2LB + 2B + 1F + 2L + 4U \\ &= 22124_{\text{five}} \end{aligned} \)
\(\begin{aligned} & 212_{\text{eight}} \times 102_{\text{eight}} = (2F + 1L + 2U) \times (1F + 2U) \\ &= 2F \times 1F + 2F \times 2U + 1L \times 1F + 1L \times 2U + 2U \times 1F + 2U \times 2U \\ &= 2LB + 4F + 1B + 2L + 2F + 4U \\ &= 2LB + 1B + 6F + 2L + 4U \\ &= 21624_{\text{eight}} \end{aligned} \)
In this last example, we got away without having to make any exchanges. We aren't so lucky in this next example, which is in base three. Base Three is harder to work with since it only takes three of something before you have to make an exchange. Sometimes it
seems that all you are doing is exchanging!
\( \begin{aligned} & 212_{\text{three}} \times 102_{\text{three}} = (2F + 1L + 2U) \times (1F + 2U) \\ &= 2F \times 1F + 2F \times 2U + 1L \times 1F + 1L \times 2U + 2U \times 1F + 2U \times 2U \\ &= 2LB + 4F + 1B + 2L + 2F + 4U \\ &= 2LB + 1B + 6F + 2L + 4U \\ &= 2LB + 1B + 2B + 2L + 1L + 1U \\ &= 2LB + 3B + 3L + 1U \\ &= 2LB + 1LB + 1F + 1U \\ &= 3LB + 1F + 1U \\ &= 1FB + 1F + 1U \\ &= 100101_{\text{three}} \end{aligned}\)
Exercise 23
Show the steps using the blocks as shown in the previous examples to multiply:
\(212_{\text{four}} \times 102_{\text{four}}\)
Exercise 24
Show the steps using the blocks as shown in the previous examples to multiply:
a. \(361_{\text{nine}} \times 15_{\text{nine}}\)
b. \(111_{\text{two}} \times 11_{\text{two}}\)
Another way to multiply with the blocks is by using a chart. This is similar to how we did it for addition. It's actually very similar to doing it using the regular multiplication algorithm, except we don't have to write the carry as we go. You simply multiply each digit of one numeral by each digit in the other numeral, and put it in the proper column. Then, you add the like terms, and still do exchanges. Here is an example writing it out with the distributive property. Below, contrast with the method using a chart.
\( \begin{aligned} & 23_{\text{six}} \times 32_{\text{six}} = (2L + 3U) \times (3L + 2U) \\ &= 2L \times 3L + 2L \times 2U + 3U \times 3L + 3U \times 2U \\ &= 6F + 4L + 9L + 6U \\ &= 6F + 13L + 6U \\ &= 1B + 2F + 1L + 1L \\ &= 1B + 2F + 2L \\ &= 1220_{\text{six}} \end{aligned}\)
In step one, the individual multiplications are done. If you get a 2-digit numeral, just write it in. No need to carry. In step 2, the like terms are added. Then, exchanges are made. I did the exchanges by exchanging the units first. In step 3, When 6 units were exchanged, I had 0 units and 1 more long, so I crossed off the 13 and put 14 in the next column to the left. In step 4, I exchanged 14 longs for 2 flats and 2 longs, so I crossed off 6 in the flat column, and added 2 more to get 8, and crossed off 14 in the long column since there were only 2 left. In the last step, 8 flats are exchanged for 1 block and 2 flats. I've shown the individual steps, all the work is shown in Step 5. That's all the space it takes.
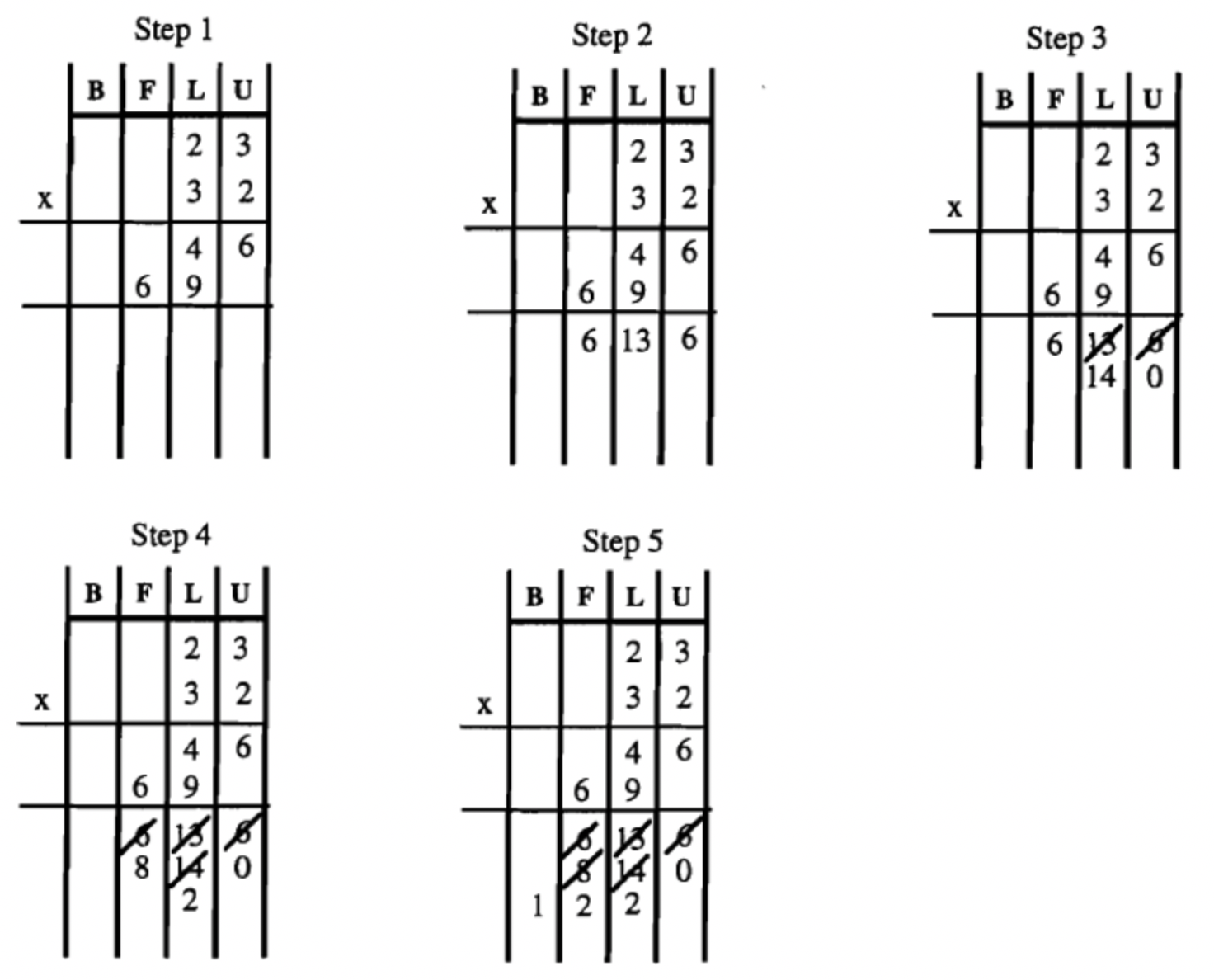
Here are three more examples of using the charts to multiply with the blocks.
| \(36_{\text{eight}} \times 45_{\text{eight}}\) | \(23_{\text{five}} \times 14_{\text{five}}\) | \(212_{\text{three}} \times 22_{\text{three}}\) |
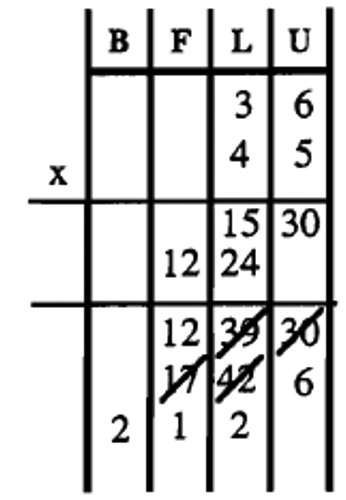 |
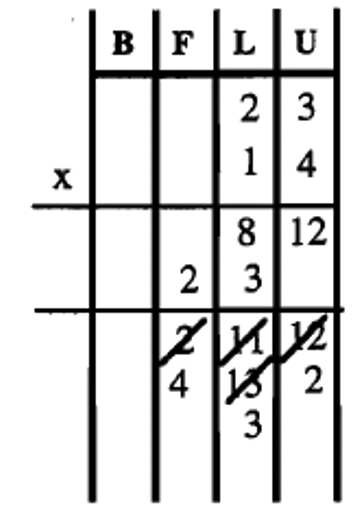 |
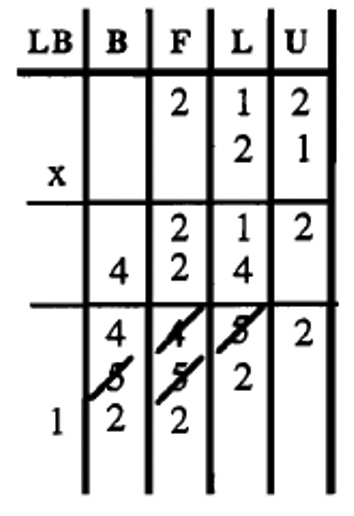 |
| = \(2126_{\text{eight}}\) | = \(432_{\text{five}}\) | = \(12222_{\text{three}}\) |
Exercise 25
Use the base block charts, writing the numbers in terms of actual base blocks at first, as shown in the above examples, to compute the following. Show all your work and steps below.
 a. \(34_{\text{six}} \times 25_{\text{six}}\) = |
 b. \(32_{\text{eleven}} \times 4T_{\text{eleven}}\) = |
 c. \(111_{\text{two}} \times 101_{\text{two}}\) = |
 d. \(1E_{\text{twelve}} \times 53_{\text{twelve}}\) = |
 e. \(212_{\text{three}} \times 22_{\text{three}}\) = |
 f. \(23_{\text{four}} \times 32_{\text{four}}\) = |
Eventually, it would be nice to be able to do the multiplications without having to think in terms of the actual blocks. The traditional algorithm could be used. To do this, you have to make sure you immediately convert to the given base before writing the answer. For instance, \(4_{\text{five}} \times 4_{\text{five}} = 31_{\text{five}}\) because 4 units times 4 units is 16 units, which in base five converts to 3 longs and 1 unit, which is written as \(31_{\text{five}}\) in base five. A good start is to make up some multiplication tables in other bases. A base seven multiplication table is shown on the next page. Keep in mind that there are seven digits in base seven, so you'll have a table to fill in that is 7 rows by 7 columns. Because of the commutative property, there is symmetry in the table, which means many answers are duplicated. Furthermore, multiplying by 0 or 1 is trivial. At the top of the table, we'll indicate it is in base seven, and then leave off writing the base to the right and below each numeral.
Table \(\PageIndex{1}\): Base Seven Multiplication Table
| \(\times\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 0 | 2 | 4 | 6 | 11 | 13 | 15 |
| 3 | 0 | 3 | 6 | 12 | 15 | 21 | 24 |
| 4 | 0 | 4 | 11 | 15 | 31 | 26 | 33 |
| 5 | 0 | 5 | 13 | 21 | 26 | 34 | 42 |
| 6 | 0 | 6 | 15 | 24 | 33 | 42 | 51 |
Make sure you don't read these as base ten numerals. 26 means "two six, base seven", which is 2 longs and 6 units, or 20 base ten units! An easy way to get started is to do the two rows and two columns where you multiply by 0 and 1, then, go down the diagonal, from upper left to bottom right. Then, fill in the numbers above the diagonal. Using the commutative property, fill in the bottom of the diagonal.
Exercise 26
Make up a multiplication table for each base indicated.
| a. Base Two Multiplication Table | b. Base Three Multiplication Table |
| c. Base Six Multiplication Table | d. Base Eight Multiplication Table |
| e. Base Twelve Multiplication Table |
If you can quickly figure out the answer to multiplying two single digits in any given base, you can now use a lattice or the standard algorithm to do multiplication in different bases. Here are some examples of multiplying numbers in different bases using the lattice method.
|
\(54_{\text{six}} \times 23_{\text{six}} = 2210_{\text{six}}\) 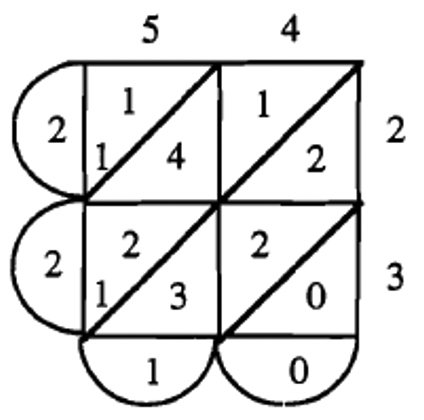 |
\(42_{\text{twelve}} \times 58_{\text{twelve}} = 1E74_{\text{twelve}}\) 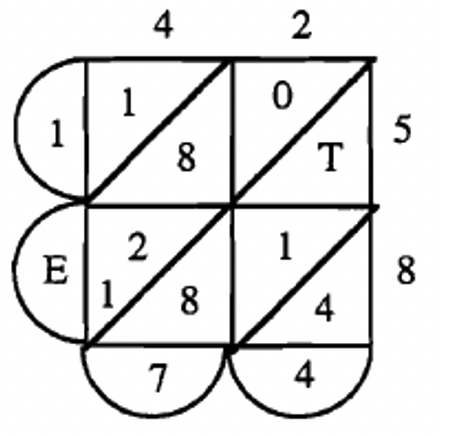 |
|
\(202_{\text{three}} \times 21_{\text{three}} = 12012_{\text{three}}\) 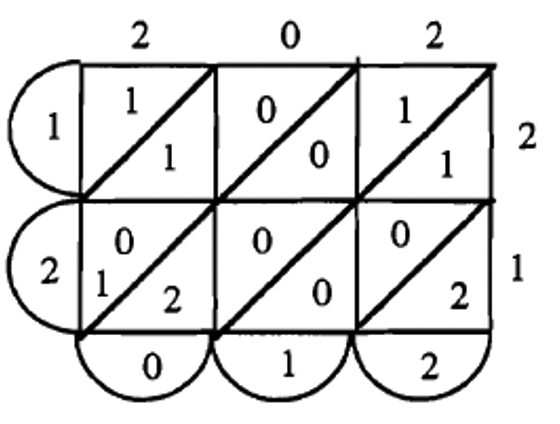 |
\(111_{\text{two}} \times 11_{\text{two}} = 10101_{\text{two}}\) 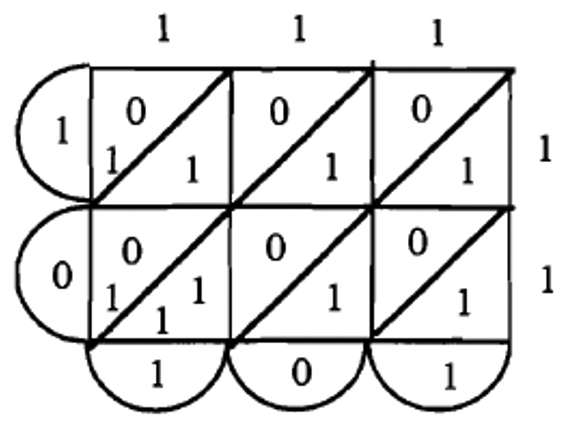 |
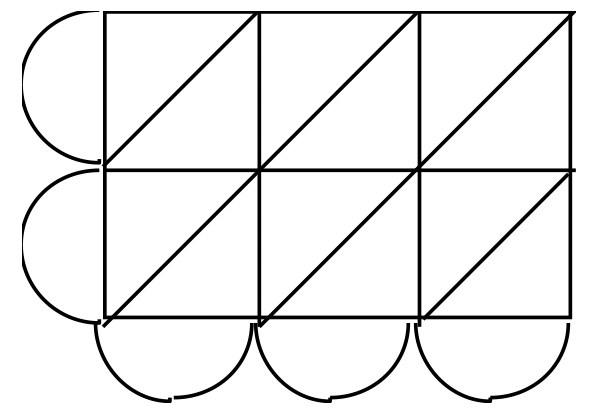
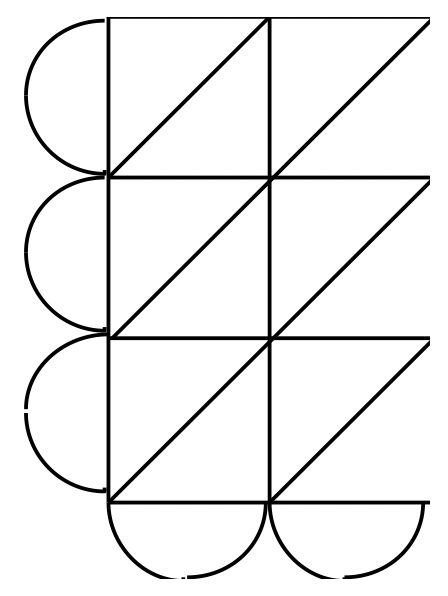
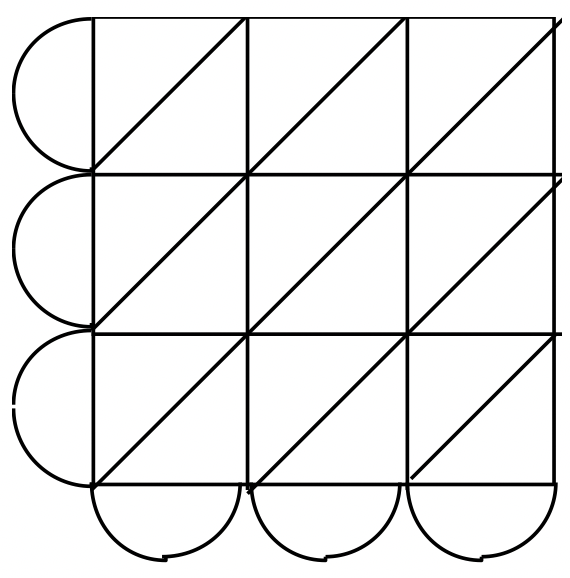
Exercise 27
Use a lattice to multiply each of the numbers in the base given.
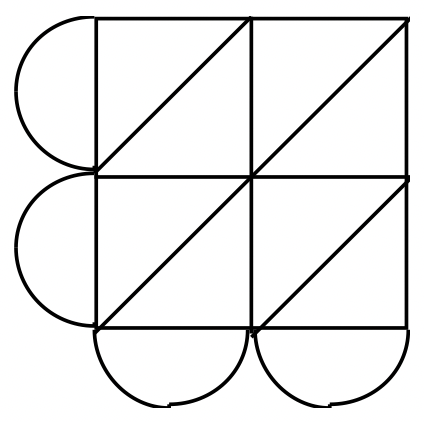 |
 |
 |
 |
 |
 |
Finally, you could use the standard multiplication algorithm with carrying. This is the shortest algorithm in terms of space on the paper, but you have to be fairly adept at mental calculations, which doesn't come naturally to most of us when working in other bases.
Before going on to the standard multiplication algorithm, we need to notice a few more things. First of all, remember when we were working with the blocks to figure out a \(L \times L\), etc.? When something was multiplied by a long, everything moved up one place value. In base ten, when you multiply a whole number by 10, the effect is that the answer is the original number with a zero tacked on to the end. That is, every digit moved up a place value. This is true in all bases. For example, \(524_{\text{seven}} \times 10_{\text{seven}} = 5240_{\text{seven}}\) and \(1T6_{\text{twelve}} \times 10_{\text{twelve}} = 1T60_{\text{twelve}}\). If you are multiplying by 100 in any base, two zeroes are tacked on to the end, and so on. This principle can be used to multiply \(2000 \times 400\) by taking advantage of the commutative and associative properties of multiplication as shown below:
\(2000 \times 400 = 2 \times 1000 \times 4 \times 100 = 2 \times 4 \times 1000 \times 100 = 8 \times 100000 = 800000\).
Of course, there is no need to write all the steps out. Simply multiply 2 times 4 and tack on five zeroes. Here's one in base eight: \(3000_{\text{eight}} \times 500_{\text{eight}} = 1700000_{\text{eight}}\).
The Partial Products Algorithm uses the above fact. Doing the partial products algorithm is similar to how we used the distributive property to multiply with the blocks (back in exercise 22). For instance, to multiply, rewrite the problem like this:
\(\begin{aligned} & 346 \times 72 = (300 + 40 + 6) \times (70 + 2) \\ &= (300 + 40 + 6) \times 70 + (300 + 40 + 6) \times 2 \\ &= 300 \times 70 + 40 \times 70 + 6 \times 70 + 300 \times 2 + 40 \times 2 + 6 \times 2 \\ &= 21000 + 2800 + 420 + 600 + 80 + 12 \\ &= 24912 \end{aligned}\)
The partial products are shown in the third line in the example above. They are:
\(300 \times 70, 40 \times 70, 6 \times 70, 300 \times 2, 40 \times 2 \text{ and } 6 \times 2\)
It's easier to write this in a vertical format. I'll show this problem two ways. It doesn't matter which partial products you multiply first. The second way it is shown is more similar to our standard algorithm, where we start with the unit's value of the bottom number and eventually work up to the larger place values.
| \(\begin{aligned} 346 \\ \times \underline{ 72} \\ 21000 && (300 \times 70) \\ 2800 && (40 \times 70) \\ 420 && (6 \times 70) \\ 600 && (300 \times 2) \\ 80 && (40 \times 2) \\ \underline{12} && (6 \times 2) \\ 24912 \end{aligned}\) | \(\begin{aligned} 346 \\ \times \underline{ 72} \\ 12 && (2 \times 6) \\ 80 && (2 \times 40) \\ 600 && (2 \times 300) \\ 420 && (70 \times 6) \\ 2800 && (70 \times 40) \\ \underline{21000} && (70 \times 300) \\ 24912 \end{aligned}\) |
On the left the first three partial products are \(346 \times 70\) and the second three partial products are \(346 \times 2\). On the right, the first three partial products are \(2 \times 346\) and the second three partial products are \(70 \times 346\).
Our standard algorithm is simply a shortening up of the partial products algorithm. We don't write all the zeroes and we doing the carrying involved with adding more than one partial product at a time in our head. Sure, it's shorter, but it is easier to make mistakes.
\(\begin{aligned} 346 \\ \times \underline{ 72} \\ 692 && (2 \times 346) \\ \underline{24220} && (70 \times 346) \\ 24912 \end{aligned}\)
Usually we just move over one place to the left to account for the zero in the one's place and don't write the zero in 24220. We "think" 7 times 346.
Exercise 28
For each problem, write out the partial products in a vertical format to multiply the numbers together. Show your work, identifying the multiplication for each partial product as shown in the example on the bottom of the previous page.
| a. \(\begin{aligned} 538 \\ \times \underline{34} \end{aligned}\) | b. \(\begin{aligned} 257 \\ \times \underline{941} \end{aligned}\) |
Finally, I'll provide some examples of what the multiplication looks like when the standard algorithm is used to multiply numbers in different bases. You have to remember to write down the number and all carries in the base you are working in. We tend to always put the numeral with the most digits on the top, but this is not necessary. Here are three ways to multiply \(563_{\text{eight}} \times 24_{\text{eight}}\).
IMPORTANT NOTE:
Each numeral below is in base eight, even though the "eight" isn't written in each intermediate step. E.g., \(4 \times 3\) in the first multiplication below, is done in base 8; therefore \(4 \times 3 = 14\).
| \(\begin{aligned} 563&_{\text{eight}} \\ \times \underline{ 24}&_{\text{eight}} \\ 2714 \\ \underline{13460} \\ 16374&_{\text{eight}} \end{aligned}\) | \(\begin{aligned} 24&_{\text{eight}} \\ \times \underline{ 563}&_{\text{eight}} \\ 74 \\ 1700 \\ \underline{14400} \\ 16374&_{\text{eight}} \end{aligned}\) | \(\begin{aligned} 563&_{\text{eight}} \\ \times \underline{ 24}&_{\text{eight}} \\ 14 && (4 \times 2) \\ 300 && (4 \times 60) \\ 2400 && (4 \times 500) \\ 60 && (20 \times 3) \\ 1400 && (20 \times 60) \\ \underline{12000} && (20 \times 500) \\ 16374&_{\text{eight}} \end{aligned}\) |
Multiply the following numbers together using two different algorithms (or switching the order of the numbers around as shown above). Show your work. Do not do it by converting each number to base ten, multiplying them together, and then convert back to the given base. Use each algorithm at least one time; lattice, partial products, standard algorithm, using the blocks with charts, using the distributive property with or without the blocks. You have lots of choices, but always keep in mind what base you are working in. You need to know all the algorithms for the exam so be sure to try them all. Okay, have fun!
Exercise 29
\(23_{\text{five}} \times 43_{\text{five}}\)
| First way: | Second way: |
Exercise 30
\(612_{\text{seven}} \times 35_{\text{seven}}\)
| First way: | Second way: |
Exercise 31
\(1011_{\text{two}} \times 1101_{\text{two}}\)
| First way: | Second way: |
Exercise 32
\(2121_{\text{three}} \times 202_{\text{three}}\)
| First way: | Second way: |
Exercise 33
\(4T1_{\text{tweleve}} \times 27_{\text{tweleve}}\)
| First way: | Second way: |
Exercise 34
\(423_{text{six}} \times 145_{\text{six}}\)
| First way: | Second way: |
Exercise 35
\(2212_{\text{three}} \times 210_{\text{three}}\)
| First way: | Second way: |
Exercise 36
\(5421_{\text{six}} \times 44_{\text{six}}\)
| First way: | Second way: |
Exercise 37
\(10110_{\text{two}} \times 1111_{\text{two}}\)
| First way: | Second way: |
Exercise 38
\(E4T_{\text{twelve}} \times E2_{\text{twelve}}\)
| First way: | Second way: |
Exercise 39
\(6661_{\text{eight}} \times 72_{\text{eight}}\)
| First way: | Second way: |
Exercise 40
\(1212_{\text{four}} \times 302_{\text{four}}\)
| First way: | Second way: |
Exercise 41
\(4234_{\text{five}} \times 244_{\text{five}}\)
| First way: | Second way: |


