4.E: Review Exercises and Sample Exam
- Last updated
- Save as PDF
- Page ID
- 61391
Review Exercises
Exercise \(\PageIndex{1}\) Rectangular Coordinate System
Graph the given set of ordered pairs.
- \(\{(−3, 4), (−4, 0), (0, 3), (2, 4)\}\)
- \(\{(−5, 5), (−3, −1), (0, 0), (3, 2)\}\)
- Graph the points \((−3, 5), (−3, −3),\) and \((3, −3)\) on a rectangular coordinate plane. Connect the points and calculate the area of the shape.
- Graph the points \((−4, 1), (0, 1), (0, −2),\) and \((−4, −2)\) on a rectangular coordinate plane. Connect the points and calculate the area of the shape.
- Graph the points \((1, 0), (4, 0), (1, −5),\) and \((4, −5)\) on a rectangular coordinate plane. Connect the points and calculate the perimeter of the shape.
- Graph the points \((−5, 2), (−5, −3), (1, 2),\) and \((1, −3)\) on a rectangular coordinate plane. Connect the points and calculate the perimeter of the shape.
- Answer
-
1.
.png?revision=1)
Figure 3.E.1
3. Area: \(24\) square units
.png?revision=1)
Figure 3.E.2
5. Perimeter: \(16\) units
.png?revision=1)
Figure 3.E.3
Exercise \(\PageIndex{2}\) Rectangular Coordinate System
Calculate the distance between the given two points.
- \((−1, −2)\) and \((5, 6)\)
- \((2, −5)\) and \((−2, −2)\)
- \((−9, −3)\) and \((−8, 4)\)
- \((−1, 3)\) and \((1, −3)\)
- Answer
-
1. \(10\) units
3. \(5\sqrt{2}\) units
Exercise \(\PageIndex{3}\) Rectangular Coordinate System
Calculate the midpoint between the given points.
- \((−1, 3)\) and \((5, −7)\)
- \((6, −3)\) and \((−8, −11)\)
- \((7, −2)\) and \((−6, −1)\)
- \((−6, 0)\) and \((0, 0)\)
- Show algebraically that the points \((−1, −1), (1, −3),\) and \((2, 0)\) form an isosceles triangle.
- Show algebraically that the points \((2, −1), (6, 1),\) and \((5, 3)\) form a right triangle.
- Answer
-
1. \((2,-2)\)
3. \((\frac{1}{2},-\frac{3}{2})\)
5. Answers may vary
Exercise \(\PageIndex{4}\) Graph by Plotting Points
Determine whether the given point is a solution.
- \(−5x+2y=7\); \((1, −1)\)
- \(6x−5y=4\); \((−1, −2)\)
- \(y=\frac{3}{4}x+1\); \((−\frac{2}{3}, \frac{1}{2})\)
- \(y=−\frac{3}{5}x−2\); \((10, −8)\)
- Answer
-
1. No
3. Yes
Exercise \(\PageIndex{5}\) Graph by Plotting Points
Find at least five ordered pair solutions and graph.
- \(y=−x+2\)
- \(y=2x−3\)
- \(y=\frac{1}{2}x−2\)
- \(y=−\frac{2}{3}x\)
- \(y=3\)
- \(x=−3\)
- \(x−5y=15\)
- \(2x−3y=12\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.4
3.
.png?revision=1)
Figure 3.E.5
5.
.png?revision=1)
Figure 3.E.6
7.
.png?revision=1)
Figure 3.E.7
Exercise \(\PageIndex{6}\) Graph Using Intercepts
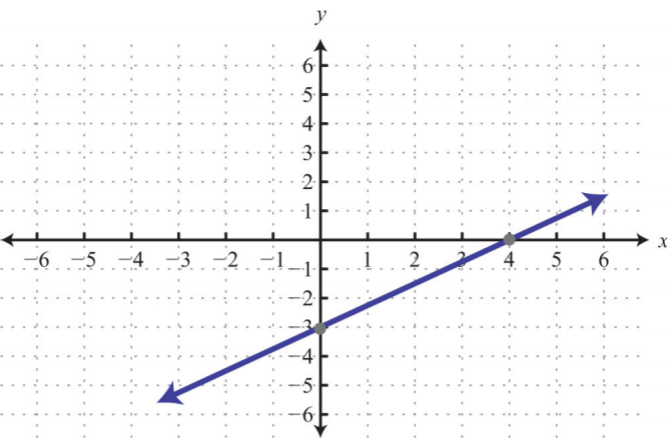
Given the graph, find the \(x\)- and \(y\)- intercepts.
1.
.png?revision=1)
Figure 3.E.8
2.
.png?revision=1)
Figure 3.E.9
3.
.png?revision=1)
Figure 3.E.10
4.
.png?revision=1)
Figure 3.E.11
- Answer
-
1. \(y\)-intercept: \((0, −2)\); \(x\)-intercept: \((−4, 0)\)
3. \(y\)-intercept: none; \(x\)-intercept: \((5, 0)\)
Exercise \(\PageIndex{7}\) Graph Using Intercepts
Find the intercepts and graph them.
- \(3x−4y=12\)
- \(2x−y=−4\)
- \(\frac{1}{2}x−\frac{1}{3}y=1\)
- \(−\frac{1}{2}x+\frac{2}{3}y=2\)
- \(y=−\frac{5}{3}x+5\)
- \(y=−3x+4\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.12
3.
.png?revision=1)
Figure 3.E.13
5.
.png?revision=1)
Figure 3.E.14
Exercise \(\PageIndex{8}\) Graph Using the \(y\)-Intercept and Slope
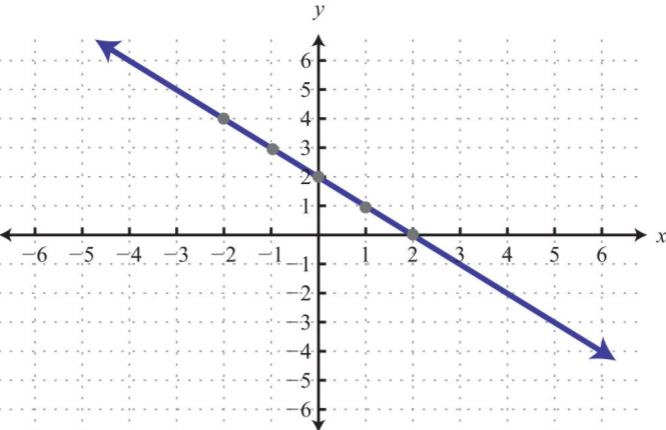
Given the graph, determine the slope and \(y\)-intercept.
1.
.png?revision=1)
Figure 3.E.15
2.
.png?revision=1)
Figure 3.E.16
- Answer
-
1. \(y\)-intercept: \((0, 1)\); slope: \(−2\)
Exercise \(\PageIndex{9}\) Graph Using the \(y\)-Intercept and Slope
Determine the slope, given two points.
- \((−3, 8)\) and \((5, −6)\)
- \((0, −5)\) and \((−6, 3)\)
- \((\frac{1}{2}, −\frac{2}{3})\) and \((\frac{1}{4}, −\frac{1}{3})\)
- \((5, −\frac{3}{4})\) and \((2, −\frac{3}{4})\)
- Answer
-
1. \(-\frac{7}{4}\)
3. \(-\frac{4}{3}\)
Exercise \(\PageIndex{10}\) Graph Using the \(y\)-Intercept and Slope
Express in slope-intercept form and identify the slope and \(y\)-intercept.
- \(12x−4y=8\)
- \(3x−6y=24\)
- \(−\frac{1}{3}x+\frac{3}{4}y=1\)
- \(−5x+3y=0\)
- Answer
-
1. \(y=3x−2\); slope: \(3\); \(y\)-intercept \((0, −2)\)
3. \(y=\frac{4}{9}x+\frac{4}{3}\); slope: \(\frac{4}{9}\); \(y\)-intercept \((0, \frac{4}{3})\)
Exercise \(\PageIndex{11}\) Graph Using the \(y\)-Intercept and Slope
- \(y=−x+3\)
- \(y=4x−1\)
- \(y=−2x\)
- \(y=−\frac{5}{2}x+3\)
- \(2x−3y=9\)
- \(2x+\frac{3}{2}y=3\)
- \(y=0\)
- \(x−4y=0\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.17
3.
.png?revision=1)
Figure 3.E.18
5.
.png?revision=1)
Figure 3.E.19
7.
.png?revision=1)
Figure 3.E.20
Exercise \(\PageIndex{12}\) Finding Linear Equations
Given the graph, determine the equation of the line.
1.
.png?revision=1)
Figure 3.E.21
2.
.png?revision=1)
Figure 3.E.22
3.
.png?revision=1)
Figure 3.E.23
4.
.png?revision=1)
Figure 3.E.24
- Answer
-
1. \(y=−2x+1\)
3. \(y=−5\)
Exercise \(\PageIndex{13}\) Finding Linear Equations
Find the equation of a line, given the slope and a point on the line.
- \(m = \frac{1}{2}\); \((−4, 8)\)
- \(m = −\frac{1}{5}\); \((−5, −9)\)
- \(m = \frac{2}{3}\); \((1, −2)\)
- \(m = −\frac{3}{4}\); \((2, −3)\)
- Answer
-
1. \(y=\frac{1}{2}x+10\)
3. \(y=\frac{2}{3}x−\frac{8}{3}\)
Exercise \(\PageIndex{14}\) Finding Linear Equations
Find the equation of the line given two points on the line.
- \((−5, −5)\) and \((10, 7)\)
- \((−6, 12)\) and \((3, −3)\)
- \((2, −1)\) and \((−2, 2)\)
- \((\frac{5}{2}, −2)\) and \((−5, \frac{5}{2})\)
- \((7, −6)\) and \((3, −6)\)
- \((10, 1)\) and \((10, −3)\)
- Answer
-
1. \(y=\frac{4}{5}x−1\)
3. \(y=−\frac{3}{4}x+\frac{1}{2}\)
5. \(y=−6\)
Exercise \(\PageIndex{15}\) Parallel and Perpendicular Lines
Determine if the lines are parallel, perpendicular, or neither.
- \(\left\{\begin{aligned}−3x+7y&=14\\6x−14y&=42\end{aligned}\right.\)
- \(\left\{\begin{aligned}2x+3y&=18\\2x−3y&=36\end{aligned}\right.\)
- \(\left\{\begin{aligned}x+4y&=2\\8x−2y=&−1\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=2\\x&=2\end{aligned}\right.\)
- Answer
-
1. Parallel
3. Perpendicular
Exercise \(\PageIndex{16}\) Parallel and Perpendicular Lines
Find the equation of the line in slope-intercept form.
- Parallel to \(5x−y=15\) and passing through \((−10, −1)\).
- Parallel to \(x−3y=1\) and passing through \((2, −2)\).
- Perpendicular to \(8x−6y=4\) and passing through \((8, −1)\).
- Perpendicular to \(7x+y=14\) and passing through \((5, 1)\).
- Parallel to \(y=1\) and passing through \((4, −1)\).
- Perpendicular to \(y=1\) and passing through \((4, −1)\).
- Answer
-
1. \(y=5x+49\)
3. \(y=−\frac{3}{4}x+5\)
5. \(y=−1\)
Exercise \(\PageIndex{17}\) Introduction to Functions
Determine the domain and range and state whether it is a function or not.
1. \(\{(−10, −1), (−5, 2), (5, 2)\}\)
2. \(\{(−12, 4), (−1, −3), (−1, −2)\}\)
3.
.png?revision=1)
Figure 3.E.25
4.
.png?revision=1)
Figure 3.E.26
5.
.png?revision=1)
Figure 3.E.27
6.
.png?revision=1)
Figure 3.E.28
- Answer
-
1. Domain: \(\{−10, −5, 5\}\); range: \(\{−1, 2\}\); function: yes
3. Domain: \(R\); range: \(R\); function: yes
5. Domain: \([−3,∞)\); range: \(R\); function: no
Exercise \(\PageIndex{18}\) Introduction to Functions
Given the following,
- \(f(x)=9x−4\), find \(f(−1)\).
- \(f(x)=−5x+1\), find \(f(−3)\).
- \(g(x)=\frac{1}{2}x−\frac{1}{3}\), find \(g(−\frac{1}{3})\).
- \(g(x)=−\frac{3}{4}x+\frac{1}{3}\), find \(g(\frac{2}{3})\).
- \(f(x)=9x−4\), find \(x\) when \(f(x)=0\).
- \(f(x)=−5x+1\), find \(x\) when \(f(x)=2\).
- \(g(x)=\frac{1}{2}x−\frac{1}{3}\), find \(x\) when \(g(x)=1\).
- \(g(x)=−\frac{3}{4}x+\frac{1}{3}\), find \(x\) when \(g(x)=−1\).
- Answer
-
1. \(f(−1)=−13\)
3. \(g(−\frac{1}{3})=−\frac{1}{2}\)
5. \(x=\frac{4}{9}\)
7. \(x=\frac{8}{3}\)
Exercise \(\PageIndex{19}\) Introduction to Functions
Given the graph of a function \(f(x)\), determine the following.
.png?revision=1)
Figure 3.E.29
- \(f(3)\)
- \(x\) when \(f(x)=4\)
- Answer
-
1. \(f(3)=−2\)
Exercise \(\PageIndex{20}\) Linear Inequalities (Two Variables)
Is the ordered pair a solution to the given inequality?
- \(6x−2y≤1\); \((−3, −7)\)
- \(−3x+y>2\); \((0, 2)\)
- \(6x−10y<-1\); \((5,-3)\)
- \(x-\frac{1}{3}y>0\); \((1, 4)\)
- \(y>0\); \((−3, −1)\)
- \(x≤−5\); \((−6, 4)\)
- Answer
-
1. Yes
3. No
5. Yes
Exercise \(\PageIndex{21}\) Linear Inequalities (Two Variables)
Graph the solution set.
- \(y≥−2x+1\)
- \(y<3x−4\)
- \(−x+y≤3\)
- \(\frac{5}{2}x+\frac{1}{2}y≤2\)
- \(3x−5y>0\)
- \(y>0\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.30
3.
.png?revision=1)
Figure 3.E.31
5.
.png?revision=1)
Figure 3.E.32
Sample Exam
Exercise \(\PageIndex{22}\)
- Graph the points \((−4, −2), (−4, 1),\) and \((0, −2)\) on a rectangular coordinate plane. Connect the points and calculate the area of the shape.
- Is \((−2, 4)\) a solution to \(3x−4y=−10\)? Justify your answer.
- Answer
-
1. Area: \(6\) square units
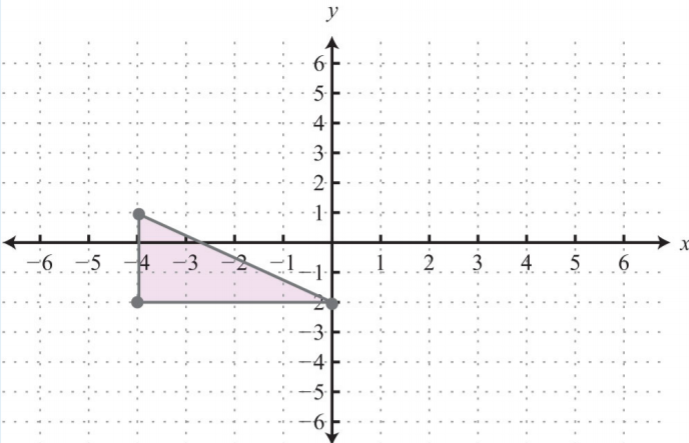.png?revision=1)
Figure 3.E.33
Exercise \(\PageIndex{23}\)
Given the set of \(x\)-values \(\{−2, −1, 0, 1, 2\}\), find the corresponding \(y\)-values and graph the following.
- \(y=x−1\)
- \(y=−x+1\)
- On the same set of axes, graph \(y=4\) and \(x=−3\). Give the point where they intersect.
- Answer
-
1.
.png?revision=1)
Figure 3.E.34
3. Intersection: \((-3,4)\)
.png?revision=1)
Figure 3.E.35
Exercise \(\PageIndex{24}\)
Find the \(x\)- and \(y\)-intercepts and use those points to graph the following.
- \(2x−y=8\)
- \(12x+5y=15\)
- Calculate the slope of the line passing through \((−4, −5)\) and \((−3, 1)\).
- Answer
-
2.
.png?revision=1)
Figure 3.E.36
Exercise \(\PageIndex{25}\)
Determine the slope and \(y\)-intercept. Use them to graph the following.
- \(y=−\frac{3}{2}x+6\)
- \(5x−2y=6\)
- Given \(m=−3\), determine \(m_{⊥}\).
- Are the given lines parallel, perpendicular, or neither? \(\left\{\begin{aligned} -2x+3y&=-12\\4x-6y&=30 \end{aligned}\right.\)
- Determine the slope of the given lines.
- \(y=−2\)
- \(x=\frac{1}{3}\)
- Are these lines parallel, perpendicular, or neither?
- Determine the equation of the line with slope \(m=−\frac{3}{4}\) passing through \((8, 1)\).
- Find the equation to the line passing through \((−2, 3)\) and \((4, 1)\).
- Find the equation of the line parallel to \(5x−y=6\) passing through \((−1, −2)\).
- Find the equation of the line perpendicular to \(−x+2y=4\) passing through \((\frac{1}{2}, 5)\).
- Answer
-
1. Slope: \(−\frac{3}{2}\); \(y\)-intercept: \((0, 6)\)
.png?revision=1)
Figure 3.E.37
3. \(m_{⊥}=\frac{1}{3}\)
5. a. \(0\); b. Undefined; c. Perpendicular
6. \(y=−\frac{3}{4}x+7\)
8. \(y=5x+3\)
Exercise \(\PageIndex{26}\)
Given a linear function \(f(x)=−\frac{4}{5}x+2\), determine the following.
- \(f(10)\)
- \(x\) when \(f(x)=0\)
- Graph the solution set: \(3x−4y>4\).
- Graph the solution set: \(y−2x≥0\).
- A rental car company charges $\(32.00\) plus $\(0.52\) per mile driven. Write an equation that gives the cost of renting the car in terms of the number of miles driven. Use the formula to determine the cost of renting the car and driving it \(46\) miles.
- A car was purchased new for $\(12,000\) and was sold 5 years later for $\(7,000\). Write a linear equation that gives the value of the car in terms of its age in years.
- The area of a rectangle is \(72\) square meters. If the width measures \(4\) meters, then determine the length of the rectangle.
- Answer
-
1. \(f(10)=−6\)
3.
.png?revision=1)
Figure 3.E.38
5. cost\(=0.52x+32\); $\(55.92\)
7. \(18\) meters

