2.EA: Exercises for Polynomials Expressions
- Page ID
- 92364
Polynomials
In Exercises 1-6, state the coefficient and the degree of each of the following terms.
1) \(3 v^{5} u^{6}\)
- Answer
-
Coefficient \(=3,\) Degree \(=11\)
2) \(-3 b^{5} z^{8}\)
3) \(-5 v^{6}\)
- Answer
-
Coefficient \(=-5,\) Degree \(=6\)
4) \(-5 c^{3}\)
5) \(2 u^{7} x^{4} d^{5}\)
- Answer
-
Coefficient \(=2,\) Degree \(=16\)
6) \(9 w^{4} c^{5} u^{7}\)
In Exercises 7-16, state whether each of the following expressions is a monomial, binomial, or trinomial.
7) \(-7 b^{9} c^{3}\)
- Answer
-
Monomial
8) \(7 b^{6} c^{2}\)
9) \(4 u+7 v\)
- Answer
-
Binomial
10) \(-3 b+5 c\)
11) \(3 b^{4}-9 b c+9 c^{2}\)
- Answer
-
Trinomial
12) \(8 u^{4}+5 u v+3 v^{4}\)
13) \(5 s^{2}+9 t^{7}\)
- Answer
-
Binomial
14) \(-8 x^{6}-6 y^{7}\)
15) \(2 u^{3}-5 u v-4 v^{4}\)
- Answer
-
Trinomial
16) \(6 y^{3}-4 y z+7 z^{3}\)
In Exercises 17-20, sort each of the given polynomials in descending powers of \(x\).
17) \(-2 x^{7}-9 x^{13}-6 x^{12}-7 x^{17}\)
- Answer
-
\(-7 x^{17}-9 x^{13}-6 x^{12}-2 x^{7}\)
18) \(2 x^{4}-8 x^{19}+3 x^{10}-4 x^{2}\)
19) \(8 x^{6}+2 x^{15}-3 x^{11}-2 x^{2}\)
- Answer
-
\(2 x^{15}-3 x^{11}+8 x^{6}-2 x^{2}\)
20) \(2 x^{6}-6 x^{7}-7 x^{15}-9 x^{18}\)
In Exercises 21-24, sort each of the given polynomials in ascending powers of \(x\).
21) \(7 x^{17}+3 x^{4}-2 x^{12}+8 x^{14}\)
- Answer
-
\(3 x^{4}-2 x^{12}+8 x^{14}+7 x^{17}\)
22) \(6 x^{18}-6 x^{4}-2 x^{19}-7 x^{14}\)
23) \(2 x^{13}+3 x^{18}+8 x^{7}+5 x^{4}\)
- Answer
-
\(5 x^{4}+8 x^{7}+2 x^{13}+3 x^{18}\)
24) \(-6 x^{18}-8 x^{11}-9 x^{15}+5 x^{12}\)
In Exercises 25-32, simplify the given polynomial, combining like terms, then arranging your answer in descending powers of \(x\).
25) \(-5 x+3-6 x^{3}+5 x^{2}-9 x+3-3 x^{2}+6 x^{3}\)
- Answer
-
\(2 x^{2}-14 x+6\)
26) \(-2 x^{3}+8 x-x^{2}+5+7+6 x^{2}+4 x^{3}-9 x\)
27) \(4 x^{3}+6 x^{2}-8 x+1+8 x^{3}-7 x^{2}+5 x-8\)
- Answer
-
\(12 x^{3}-x^{2}-3 x-7\)
28) \(-8 x^{3}-2 x^{2}-7 x-3+7 x^{3}-9 x^{2}-8 x+9\)
29) \(x^{2}+9 x-3+7 x^{2}-3 x-8\)
- Answer
-
\(8 x^{2}+6 x-11\)
30) \(-4 x^{2}-6 x+3-3 x^{2}+3 x-6\)
31) \(8 x+7+2 x^{2}-8 x-3 x^{3}-x^{2}\)
- Answer
-
\(-3 x^{3}+x^{2}+7\)
32) \(-x^{2}+8-7 x+8 x-5 x^{2}+4 x^{3}\)
In Exercises 33-44, simplify the given polynomial, combining like terms, then arranging your answer in a reasonable order, perhaps in descending powers of either variable. Note: Answers may vary, depending on which variable you choose to dictate the order.
33) \(-8 x^{2}-4 x z-2 z^{2}-3 x^{2}-8 x z+2 z^{2}\)
- Answer
-
\(-11 x^{2}-12 x z\)
34) \(-5 x^{2}+9 x z-4 z^{2}-6 x^{2}-7 x z+7 z^{2}\)
35) \(-6 u^{3}+4 u v^{2}-2 v^{3}-u^{3}+6 u^{2} v-5 u v^{2}\)
- Answer
-
\(-7 u^{3}+6 u^{2} v-u v^{2}-2 v^{3}\)
36) \(7 a^{3}+6 a^{2} b-5 a b^{2}+4 a^{3}+6 a^{2} b+6 b^{3}\)
37) \(-4 b^{2} c-3 b c^{2}-5 c^{3}+9 b^{3}-3 b^{2} c+5 b c^{2}\)
- Answer
-
\(9 b^{3}-7 b^{2} c+2 b c^{2}-5 c^{3}\)
38) \(4 b^{3}-6 b^{2} c+9 b c^{2}-9 b^{3}-8 b c^{2}+3 c^{3}\)
39) \(-8 y^{2}+6 y z-7 z^{2}-2 y^{2}-3 y z-9 z^{2}\)
- Answer
-
\(-10 y^{2}+3 y z-16 z^{2}\)
40) \(8 x^{2}+x y+3 y^{2}-x^{2}+7 x y+y^{2}\)
41) \(7 b^{2} c+8 b c^{2}-6 c^{3}-4 b^{3}+9 b c^{2}-6 c^{3}\)
- Answer
-
\(-4 b^{3}+7 b^{2} c+17 b c^{2}-12 c^{3}\)
42) \(7 x^{3}-9 x^{2} y+3 y^{3}+7 x^{3}+3 x y^{2}-7 y^{3}\)
43) \(9 a^{2}+a c-9 c^{2}-5 a^{2}-2 a c+2 c^{2}\)
- Answer
-
\(4 a^{2}-a c-7 c^{2}\)
44) \(7 u^{2}+3 u v-6 v^{2}-6 u^{2}+7 u v+6 v^{2}\)
In Exercises 45-50, state the degree of the given polynomial.
45) \(3 x^{15}+4+8 x^{3}-8 x^{19}\)
- Answer
-
\(19\)
46) \(-4 x^{6}-7 x^{16}-5+3 x^{18}\)
47) \(7 x^{10}-3 x^{18}+9 x^{4}-6\)
- Answer
-
\(18\)
48) \(3 x^{16}-8 x^{5}+x^{8}+7\)
49) \(-2-x^{7}-5 x^{5}+x^{10}\)
- Answer
-
\(10\)
50) \(x^{11}+7 x^{16}+8-7 x^{10}\)
51) Given \(f(x)=5 x^{3}+4 x^{2}-6\), evaluate \(f(-1)\).
- Answer
-
\(-7\)
52) Given \(f(x)=-3 x^{3}+3 x^{2}-9\), evaluate \(f(-1)\).
53) Given \(f(x)=5 x^{4}-4 x-6\), evaluate \(f(-2)\).
- Answer
-
\(82\)
54) Given \(f(x)=-2 x^{4}-4 x-9\), evaluate \(f(2)\).
55) Given \(f(x)=3 x^{4}+5 x^{3}-9\), evaluate \(f(-2)\).
- Answer
-
\(-1\)
56) Given \(f(x)=-3 x^{4}+2 x^{3}-6\), evaluate \(f(-1)\).
57) Given \(f(x)=3 x^{4}-5 x^{2}+8\), evaluate \(f(-1)\).
- Answer
-
\(6\)
58) Given \(f(x)=-4 x^{4}-5 x^{2}-3\), evaluate \(f(3)\).
59) Given \(f(x)=-2 x^{3}+4 x-9\), evaluate \(f(2)\).
- Answer
-
\(-17\)
60) Given \(f(x)=4 x^{3}+3 x+7\), evaluate \(f(-2)\).
In Exercises 61-64, use your graphing calculator to sketch the given quadratic polynomial. In each case the graph is a parabola, so adjust the WINDOW parameters until the vertex is visible in the viewing window, as needed.
61) \(p(x)=-2 x^{2}+8 x+32\)
- Answer
-
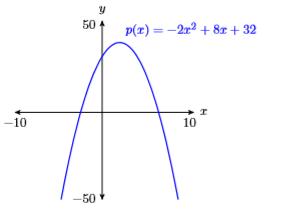
62) \(p(x)=2 x^{2}+6 x-18\)
63) \(p(x)=3 x^{2}-8 x-35\)
- Answer
-
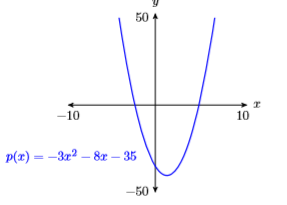
64) \(p(x)=-4 x^{2}-9 x+50\)
In Exercises 65-68, use your graphing calculator to sketch the polynomial using the given WINDOW parameters.
65) \(p(x)=x^{3}-4 x^{2}-11 x+30\)
\(\mathbf{X} \min =-10 \quad \mathbf{X} \max =10\)
\(\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50\)
- Answer
-
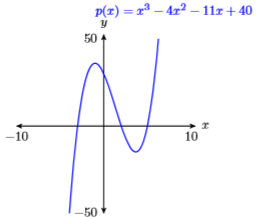
66) \(p(x)=-x^{3}+4 x^{2}+27 x-90\)
\(\mathbf{X} \min =-10 \quad \mathbf{X} \max =10\)
\(\mathbf{Y} \min =-150 \quad \mathbf{Y} \max =50\)
67) \(p(x)=x^{4}-10 x^{3}-4 x^{2}+250 x-525\)
\(\mathbf{X} \min =-10 \quad \mathbf{X} \max =10\)
\(\mathbf{Y} \min =-1000 \quad \mathbf{Y} \max =500\)
- Answer
-
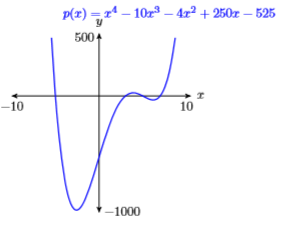
68) \(p(x)=-x^{4}+2 x^{3}+35 x^{2}-36 x-180\)
\(\mathbf{X} \min =-10 \quad \mathbf{X} \max =10\)
\(\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50\)
Adding and Subtracting Polynomials
In Exercises 1-8, simplify the given expression. Arrange your answer in some sort of reasonable order.
1) \(\left(-8 r^{2} t+7 r t^{2}+3 t^{3}\right)+\left(9 r^{3}+2 r t^{2}+4 t^{3}\right)\)
- Answer
-
\(9 r^{3}-8 r^{2} t+9 r t^{2}+7 t^{3}\)
2) \(\left(-a^{3}-8 a c^{2}-7 c^{3}\right)+\left(-7 a^{3}-8 a^{2} c+8 a c^{2}\right)\)
3) \(\left(7 x^{2}-6 x-9\right)+\left(8 x^{2}+10 x+9\right)\)
- Answer
-
\(15 x^{2}+4 x\)
4) \(\left(-7 x^{2}+5 x-6\right)+\left(-10 x^{2}-1\right)\)
5) \(\left(-2 r^{2}+7 r s+4 s^{2}\right)+\left(-9 r^{2}+7 r s-2 s^{2}\right)\)
- Answer
-
\(-11 r^{2}+14 r s+2 s^{2}\)
6) \(\left(-2 r^{2}+3 r t-4 t^{2}\right)+\left(7 r^{2}+4 r t-7 t^{2}\right)\)
7) \(\left(-8 y^{3}-3 y^{2} z-6 z^{3}\right)+\left(-3 y^{3}+7 y^{2} z-9 y z^{2}\right)\)
- Answer
-
\(-11 y^{3}+4 y^{2} z-9 y z^{2}-6 z^{3}\)
8) \(\left(7 y^{2} z+8 y z^{2}+2 z^{3}\right)+\left(8 y^{3}-8 y^{2} z+9 y z^{2}\right)\)
In Exercises 9-14, simplify the given expression by distributing the minus sign.
9) \(-\left(5 x^{2}-4\right)\)
- Answer
-
\(-5 x^{2}+4\)
10) \(-\left(-8 x^{2}-5\right)\)
11) \(-\left(9 r^{3}-4 r^{2} t-3 r t^{2}+4 t^{3}\right)\)
- Answer
-
\(-9 r^{3}+4 r^{2} t+3 r t^{2}-4 t^{3}\)
12) \(-\left(7 u^{3}-8 u^{2} v+6 u v^{2}+5 v^{3}\right)\)
13) \(-\left(-5 x^{2}+9 x y+6 y^{2}\right)\)
- Answer
-
\(5 x^{2}-9 x y-6 y^{2}\)
14) \(-\left(-4 u^{2}-6 u v+5 v^{2}\right)\)
In Exercises 15-22, simplify the given expression. Arrange your answer in some sort of reasonable order.
15) \(\left(-u^{3}-4 u^{2} w+7 w^{3}\right)-\left(u^{2} w+u w^{2}+3 w^{3}\right)\)
- Answer
-
\(-u^{3}-5 u^{2} w-u w^{2}+4 w^{3}\)
16) \(\left(-b^{2} c+8 b c^{2}+8 c^{3}\right)-\left(6 b^{3}+b^{2} c-4 b c^{2}\right)\)
17) \(\left(2 y^{3}-2 y^{2} z+3 z^{3}\right)-\left(-8 y^{3}+5 y z^{2}-3 z^{3}\right)\)
- Answer
-
\(10 y^{3}-2 y^{2} z-5 y z^{2}+6 z^{3}\)
18) \(\left(4 a^{3}+6 a c^{2}+5 c^{3}\right)-\left(2 a^{3}+8 a^{2} c-7 a c^{2}\right)\)
19) \(\left(-7 r^{2}-9 r s-2 s^{2}\right)-\left(-8 r^{2}-7 r s+9 s^{2}\right)\)
- Answer
-
\(r^{2}-2 r s-11 s^{2}\)
20) \(\left(-4 a^{2}+5 a b-2 b^{2}\right)-\left(-8 a^{2}+7 a b+2 b^{2}\right)\)
21) \(\left(10 x^{2}+2 x-6\right)-\left(-8 x^{2}+14 x+17\right)\)
- Answer
-
\(18 x^{2}-12 x-23\)
22) \(\left(-5 x^{2}+19 x-5\right)-\left(-15 x^{2}+19 x+8\right)\)
In Exercises 23-28, for the given polynomial functions \(f(x)\) and \(g(x)\), simplify \(f(x)+g(x)\). Arrange your answer in descending powers of \(x\).
23) \(\begin{aligned}f(x)&=-2 x^{2}+9 x+7 \\ g(x)&=8 x^{3}-7 x^{2}+5\end{aligned}\)
- Answer
-
\(8 x^{3}-9 x^{2}+9 x+12\)
24) \(\begin{aligned}f(x)&=-8 x^{3}+6 x-9 \\ g(x)&=x^{3}-x^{2}+3 x\end{aligned}\)
25) \(\begin{aligned}f(x)&=5 x^{3}-5 x^{2}+8 x \\ g(x)&=7 x^{2}-2 x-9\end{aligned}\)
- Answer
-
\(5 x^{3}+2 x^{2}+6 x-9\)
26) \(\begin{aligned}f(x)&=-x^{2}+8 x+1 \\ g(x)&=-7 x^{3}+8 x-9\end{aligned}\)
27) \(\begin{aligned}f(x)&=-3 x^{2}-8 x-9 \\ g(x)&=5 x^{2}-4 x+4\end{aligned}\)
- Answer
-
\(2 x^{2}-12 x-5\)
28) \(\begin{aligned}f(x)&=-3 x^{2}+x-8 \\ g(x)&=7 x^{2}-9\end{aligned}\)
In Exercises 29-34, for the given polynomial functions \(f(x)\) and \(g(x)\), simplify \(f(x)−g(x)\). Arrange your answer in descending powers of \(x\).
29) \(\begin{aligned}f(x)&=-6 x^{3}-7 x+7 \\ g(x)&=-3 x^{3}-3 x^{2}-8 x\end{aligned}\)
- Answer
-
\(-3 x^{3}+3 x^{2}+x+7\)
30) \(\begin{aligned}f(x)&=5 x^{3}-5 x+4 \\ g(x)&=-8 x^{3}-2 x^{2}-3 x\end{aligned}\)
31) \(\begin{aligned}f(x)&=12 x^{2}-5 x+4 \\ g(x)&=8 x^{2}-16 x-7\end{aligned}\)
- Answer
-
\(4 x^{2}+11 x+11\)
32) \(\begin{aligned}f(x)&=-7 x^{2}+12 x+17 \\ g(x)&=-10 x^{2}-17\end{aligned}\)
33) \(\begin{aligned}f(x)&=-3 x^{3}-4 x+2 \\ g(x)&=-4 x^{3}-7 x^{2}+6\end{aligned}\)
- Answer
-
\(x^{3}+7 x^{2}-4 x-4\)
34) \(\begin{aligned}f(x)&=-9 x^{2}+9 x+3 \\ g(x)&=7 x^{3}+7 x^{2}+5\end{aligned}\)
In Exercises 35-36, find the area of the given square by summing the areas of its four parts.
35)
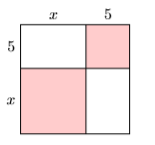
- Answer
-
\(x^{2}+10 x+25\)
36)
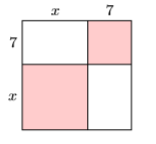
Laws of Exponents
In Exercises 1-8, simplify each of the given exponential expressions.
1) \((-4)^{3}\)
- Answer
-
\(-64\)
2) \((-9)^{2}\)
3) \(\left(-\dfrac{5}{7}\right)^{0}\)
- Answer
-
\(1\)
4) \(\left(-\dfrac{2}{5}\right)^{0}\)
5) \(\left(-\dfrac{4}{3}\right)^{2}\)
- Answer
-
\(\dfrac{16}{9}\)
6) \(\left(-\dfrac{2}{3}\right)^{2}\)
7) \((-19)^{0}\)
- Answer
-
\(1\)
8) \((-17)^{0}\)
In Exercises 9-18, simplify each of the given exponential expressions.
9) \((7 v-6 w)^{18} \cdot(7 v-6 w)^{17}\)
- Answer
-
\((7 v-6 w)^{35}\)
10) \((8 a+7 c)^{3} \cdot(8 a+7 c)^{19}\)
11) \(3^{4} \cdot 3^{0}\)
- Answer
-
\(3^{4}\)
12) \(5^{7} \cdot 5^{0}\)
13) \(4^{n} \cdot 4^{8 n+3}\)
- Answer
-
\(4^{9 n+3}\)
14) \(4^{6 m+5} \cdot 4^{m-5}\)
15) \(x^{8} \cdot x^{3}\)
- Answer
-
\(x^{11}\)
16) \(a^{9} \cdot a^{15}\)
17) \(2^{5} \cdot 2^{3}\)
- Answer
-
\(2^{8}\)
18) \(2^{10} \cdot 2^{3}\)
In Exercises 19-28, simplify each of the given exponential expressions.
19) \(\dfrac{4^{16}}{4^{16}}\)
- Answer
-
\(1\)
20) \(\dfrac{3^{12}}{3^{12}}\)
21) \(\dfrac{w^{11}}{w^{7}}\)
- Answer
-
\(w^{4}\)
22) \(\dfrac{c^{10}}{c^{8}}\)
23) \(\dfrac{(9 a-8 c)^{15}}{(9 a-8 c)^{8}}\)
- Answer
-
\((9 a-8 c)^{7}\)
24) \(\dfrac{(4 b+7 c)^{15}}{(4 b+7 c)^{5}}\)
25) \(\dfrac{2^{9 n+5}}{2^{3 n-4}}\)
- Answer
-
\(2^{6 n+9}\)
26) \(\dfrac{2^{4 k-9}}{2^{3 k-8}}\)
27) \(\dfrac{4^{17}}{4^{9}}\)
- Answer
-
\(4^{8}\)
28) \(\dfrac{2^{17}}{2^{6}}\)
In Exercises 29-38, simplify each of the given exponential expressions.
29) \(\left(4^{8 m-6}\right)^{7}\)
- Answer
-
\(4^{56 m-42}\)
30) \(\left(2^{2 m-9}\right)^{3}\)
31) \(\left[(9 x+5 y)^{3}\right]^{7}\)
- Answer
-
\((9 x+5 y)^{21}\)
32) \(\left[(4 u-v)^{8}\right]^{9}\)
33) \(\left(4^{3}\right)^{2}\)
- Answer
-
\(4^{6}\)
34) \(\left(3^{4}\right)^{2}\)
35) \(\left(c^{4}\right)^{7}\)
- Answer
-
\(c^{28}\)
36) \(\left(w^{9}\right)^{5}\)
37) \(\left(6^{2}\right)^{0}\)
- Answer
-
\(1\)
38) \(\left(8^{9}\right)^{0}\)
In Exercises 39-48, simplify each of the given exponential expressions.
39) \((u w)^{5}\)
- Answer
-
\(u^{5} w^{5}\)
40) \((a c)^{4}\)
41) \((-2 y)^{3}\)
- Answer
-
\(-8 y^{3}\)
42) \((-2 b)^{3}\)
43) \(\left(3 w^{9}\right)^{4}\)
- Answer
-
\(81 w^{36}\)
44) \(\left(-3 u^{9}\right)^{4}\)
45) \(\left(-3 x^{8} y^{2}\right)^{4}\)
- Answer
-
\(81 x^{32} y^{8}\)
46) \(\left(2 x^{8} z^{6}\right)^{4}\)
47) \(\left(7 s^{6 n}\right)^{3}\)
- Answer
-
\(343 s^{18 n}\)
48) \(\left(9 b^{6 n}\right)^{3}\)
In Exercises 49-56, simplify each of the given exponential expressions.
49) \(\left(\dfrac{v}{2}\right)^{3}\)
- Answer
-
\(\dfrac{v^{3}}{8}\)
50) \(\left(\dfrac{t}{9}\right)^{2}\)
51) \(\left(-\dfrac{2}{u}\right)^{2}\)
- Answer
-
\(\dfrac{4}{u^{2}}\)
52) \(\left(-\dfrac{3}{w}\right)^{3}\)
53) \(\left(-\dfrac{r^{8}}{5}\right)^{4}\)
- Answer
-
\(\dfrac{r^{32}}{625}\)
54) \(\left(-\dfrac{x^{11}}{5}\right)^{5}\)
55) \(\left(\dfrac{5}{c^{9}}\right)^{4}\)
- Answer
-
\(\dfrac{625}{c^{36}}\)
56) \(\left(\dfrac{5}{u^{12}}\right)^{2}\)
57) Complete each of the laws of exponents presented in the first column, then use the results to simplify the expressions in the second column.
| \(a^{m} a^{n}=?\) | \(a^{3} a^{5}=?\) |
| \(\dfrac{a^{m}}{a^{n}}=?\) | \(\dfrac{a^{6}}{a^{2}}=?\) |
| \(\left(a^{m}\right)^{n}=?\) | \(\left(a^{5}\right)^{7}=?\) |
| \((a b)^{m}=?\) | \((a b)^{9}=?\) |
| \(\left(\dfrac{a}{b}\right)^{m}=?\) | \(\left(\dfrac{a}{b}\right)^{3}=?\) |
- Answer
-
The general answers are: \(a^{m+n}, a^{m-n}, a^{m n}, a^{m} b^{m}, \dfrac{a^m}{b^m}\).
The specific answers are: \(a^{8}, a^{4}, a^{35}, a^{9} b^{9}, \dfrac{a^3}{b^3}\).
Multiplying Polynomials
In Exercises 1-10, simplify the given expression.
1) \(-3(7 r)\)
- Answer
-
\(-21 r\)
2) \(7(3 a)\)
3) \(\left(-9 b^{3}\right)\left(-8 b^{6}\right)\)
- Answer
-
\(72b^{9}\)
4) \(\left(8 s^{3}\right)\left(-7 s^{4}\right)\)
5) \(\left(-7 r^{2} t^{4}\right)\left(7 r^{5} t^{2}\right)\)
- Answer
-
\(-49 r^{7} t^{6}\)
6) \(\left(-10 s^{2} t^{8}\right)\left(-7 s^{4} t^{3}\right)\)
7) \(\left(-5 b^{2} c^{9}\right)\left(-8 b^{4} c^{4}\right)\)
- Answer
-
\(40 b^{6} c^{13}\)
8) \(\left(-9 s^{2} t^{8}\right)\left(7 s^{5} t^{4}\right)\)
9) \(\left(-8 v^{3}\right)\left(4 v^{4}\right)\)
- Answer
-
\(-32 v^{7}\)
10) \(\left(-9 y^{3}\right)\left(3 y^{5}\right)\)
In exercises 11-50, multiply to expand the given expression.
11) \(9\left(-2 b^{2}+2 b+9\right)\)
- Answer
-
\(-18 b^{2}+18 b+81\)
12) \(9\left(-4 b^{2}+7 b-8\right)\)
13) \(-4\left(10 t^{2}-7 t-6\right)\)
- Answer
-
\(-40 t^{2}+28 t+24\)
14) \(-5\left(-7 u^{2}-7 u+2\right)\)
15) \(-8 u^{2}\left(-7 u^{3}-8 u^{2}-2 u+10\right)\)
- Answer
-
\(56 u^{5}+64 u^{4}+16 u^{3}-80 u^{2}\)
16) \(-3 s^{2}\left(-7 s^{3}-9 s^{2}+6 s+3\right)\)
17) \(10 s^{2}\left(-10 s^{3}+2 s^{2}+2 s+8\right)\)
- Answer
-
\(-100 s^{5}+20 s^{4}+20 s^{3}+80 s^{2}\)
18) \(8 u^{2}\left(9 u^{3}-5 u^{2}-2 u+5\right)\)
19) \(2 s t\left(-4 s^{2}+8 s t-10 t^{2}\right)\)
- Answer
-
\(-8 s^{3} t+16 s^{2} t^{2}-20 s t^{3}\)
20) \(7 u v\left(-9 u^{2}-3 u v+4 v^{2}\right)\)
21) \(-2 u w\left(10 u^{2}-7 u w-2 w^{2}\right)\)
- Answer
-
\(-20 u^{3} w+14 u^{2} w^{2}+4 u w^{3}\)
22) \(-6 v w\left(-5 v^{2}+9 v w+5 w^{2}\right)\)
23) \((-9 x-4)(-3 x+2)\)
- Answer
-
\(27 x^{2}-6 x-8\)
24) \((4 x-10)(-2 x-6)\)
25) \((3 x+8)(3 x-2)\)
- Answer
-
\(9 x^{2}+18 x-16\)
26) \((-6 x+8)(-x+1)\)
27) \(-12 x^{3}+14 x^{2}+6 x-5\)
- Answer
-
\(-\dfrac{930}{289}\)
28) \((4 x-6)\left(-7 x^{2}-10 x+10\right)\)
29) \((x-6)\left(-2 x^{2}-4 x-4\right)\)
- Answer
-
\(-2 x^{3}+8 x^{2}+20 x+24\)
30) \((5 x-10)\left(-3 x^{2}+7 x-8\right)\)
31) \((8 u-9 w)(8 u-9 w)\)
- Answer
-
\(64 u^{2}-144 u w+81 w^{2}\)
32) \((3 b+4 c)(-8 b+10 c)\)
33) \((9 r-7 t)(3 r-9 t)\)
- Answer
-
\(27 r^{2}-102 r t+63 t^{2}\)
34) \((-6 x-3 y)(-6 x+9 y)\)
35) \((4 r-10 s)\left(-10 r^{2}+10 r s-7 s^{2}\right)\)
- Answer
-
\(-40 r^{3}+140 r^{2} s-128 r s^{2}+70 s^{3}\)
36) \((5 s-9 t)\left(-3 s^{2}+4 s t-9 t^{2}\right)\)
37) \((9 x-2 z)\left(4 x^{2}-4 x z-10 z^{2}\right)\)
- Answer
-
\(36 x^{3}-44 x^{2} z-82 x z^{2}+20 z^{3}\)
38) \((r-4 t)\left(7 r^{2}+4 r t-2 t^{2}\right)\)
39) \((9 r+3 t)^{2}\)
- Answer
-
\(81 r^{2}+54 r t+9 t^{2}\)
40) \((4 x+8 z)^{2}\)
41) \((4 y+5 z)(4 y-5 z)\)
- Answer
-
\(16 y^{2}-25 z^{2}\)
42) \((7 v+2 w)(7 v-2 w)\)
43) \((7 u+8 v)(7 u-8 v)\)
- Answer
-
\(49 u^{2}-64 v^{2}\)
44) \((6 b+8 c)(6 b-8 c)\)
45) \((7 b+8 c)^{2}\)
- Answer
-
\(49 b^{2}+112 b c+64 c^{2}\)
46) \((2 b+9 c)^{2}\)
47) \(\left(2 t^{2}+9 t+4\right)\left(2 t^{2}+9 t+4\right)\)
- Answer
-
\(4 t^{4}+36 t^{3}+97 t^{2}+72 t+16\)
48) \(\left(3 a^{2}-9 a+4\right)\left(3 a^{2}-9 a+2\right)\)
49) \(\left(4 w^{2}+3 w+5\right)\left(3 w^{2}-6 w+8\right)\)
- Answer
-
\(12 w^{4}-15 w^{3}+29 w^{2}-6 w+40\)
50) \(\left(4 s^{2}+3 s+8\right)\left(2 s^{2}+4 s-9\right)\)


