3.3: Functions and Function Notation

Last updated
Save as PDF

Page ID: 87080

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Determine whether a relation represents a function.
Evaluate functions.
Find domain of functions.

Are You Ready?

Try these questions prior to beginning this section to help determine if you are set up for success:

Evaluate the expression at the given value: \[x^2-8x-13 \text{ at } x=-1\nonumber\]
Simplify:
1. $\quad -4-(b-1)^2$
2. $\quad\dfrac{3}{3-m}-\dfrac{2m}{m+3}+\dfrac{12-8m}{m^2-9}$
3. $\quad\dfrac{1-\frac{4}{t^2}}{1-\frac{2}{t}}$
Solve: \[2y^3-3y^2=8y-12\nonumber\]
Solve the inequality and write your answer in interval notation: \[x(6x+1) \geq 12 \nonumber\]

Answer

$-4$

If you missed this problem or feel you could use more practice, review [2.3: Polynomial Expressions]

1. $\quad -b^2+2b-5$. If you missed this problem or feel you could use more practice, review [2.6: Multiplying Polynomial Expressions]
2. $\quad -\dfrac{2m-1}{m-3} \nonumber$. If you missed this problem or feel you could use more practice, review [2.14: Adding and Subtracting Rational Expressions]
3. $\quad\dfrac{t+2}{t} \nonumber$. If you missed this problem or feel you could use more practice, review [2.15: Simplifying Complex Rational Expressions]

$y=-2 \text{, } 0 \text{, } \dfrac{3}{2} $

If you missed this problem or feel you could use more practice, review [2.8: Solving Polynomial Equations and 2.12: General Strategy for Factoring Polynomials]

$\left(-\infty,-\dfrac{3}{2}\right) \cup \left(-\dfrac{3}{2},\dfrac{4}{3}\right) \cup \left(\dfrac{4}{3},\infty\right)$

If you missed this problem or feel you could use more practice, review [3.2: Solving Nonlinear Inequalities]

Imagine visiting a faraway city or even outer space from the comfort of your living room. It could be possible using virtual reality. This technology creates realistic images that make you feel as if you are truly immersed in the scene and even enable you to interact with them. It is being developed for fun applications, such as video games, but also for architects to plan buildings, car companies to design prototypes, the military to train, and medical students to learn. Developing virtual reality devices requires modeling the environment using functions.

Person wearing a virtual reality headset — Figure $\PageIndex{1}$: This odd-looking headgear provides the user with a virtual world. (credit: fill/Pixabay)

What is a Function?

The natural world is full of relationships between quantities that change. When we see these relationships, it is natural for us to ask "If I know one quantity, can I then determine the other?" This establishes the idea of an input quantity, or independent variable, and a corresponding output quantity, or dependent variable. From this we get the notion of a functional relationship in which the output can be determined from the input.

For some quantities, like height and age, there are certainly relationships between these quantities. Given a specific person and any age, it is easy enough to determine their height, but if we tried to reverse that relationship and determine age from a given height, that would be problematic, since most people maintain the same height for many years.

Determining Whether a Relation Represents a Function

A relation is a set of ordered pairs. The set of the first components of the ordered pairs is called the domain and the set of the second components of the ordered pairs is called the range.

Consider the following set of ordered pairs: $\{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)\}$

The domain is $\{1, 2, 3, 4, 5\}$. The range is $\{2, 4, 6, 8, 10\}$.

Each value in the domain is also known as an input value. Each value in the range is also known as an output value.

A function is a relation that assigns each value in the domain to a single value in the range.

To determine if a relation represents a function we can use a mapping diagram.

Figure $\PageIndex{1}$ shows mapping diagrams for relations that are functions and are not functions.

Function

A function is a relation in which each input value in the domain is assigned to exactly one output value in the range. We say “the output is a function of the input.”

The set of all input values are called the domain values, and the set of all output values are called the range values.

Example $\PageIndex{1}$

The coffee shop menu, shown in Figure $\PageIndex{2}$ consists of items and their prices.

Is price a function of the item?
Is the item a function of the price?

Figure $\PageIndex{2}$: A menu of donut prices from a coffee shop where a plain donut is $1.49 and a jelly donut and chocolate donut are $1.99.

Solution

Let’s begin by considering the input as the items on the menu. The output values are then the prices. See Figure $\PageIndex{3}$.

Each item on the menu has only one price, so the price is a function of the item.

Two items on the menu have the same price. If we consider the prices to be the input values and the items to be the output, then the same input value could have more than one output associated with it. See Figure $\PageIndex{4}$.

[Association of the prices to the donuts.] — Figure $\PageIndex{4}$: Association of the prices to the donuts.

Therefore, the item is a not a function of price.

Example $\PageIndex{2}$

In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? Table $\PageIndex{1}$ shows a possible rule for assigning grade points.

Table $\PageIndex{1}$: Class grade points.
Percent grade	0–56	57–61	62–66	67–71	72–77	78–86	87–91	92–100
Grade point average	0.0	1.0	1.5	2.0	2.5	3.0	3.5	4.0

Solution

For any percent grade earned, there is an associated grade point average, so the grade point average is a function of the percent grade. In other words, if we input the percent grade, the output is a specific grade point average.

In the grading system given, there is a range of percent grades that correspond to the same grade point average. For example, students who receive a grade point average of 3.0 could have a variety of percent grades ranging from 78 all the way to 86. Thus, percent grade is not a function of grade point average.

You Try $\PageIndex{1}$

Table $\PageIndex{2}$ lists the five greatest baseball players of all time in order of rank.

Table $\PageIndex{2}$: Five greatest baseball players.
Player	Rank
Babe Ruth	1
Willie Mays	2
Ty Cobb	3
Walter Johnson	4
Hank Aaron	5

Is the rank a function of the player name?
Is the player name a function of the rank?

Answer a: Yes
Answer b: Yes. (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)

Function Notation

Once we determine that a relation is a function of the input, we can define a name to describe this relationship. This is especially useful in programming. We typically use a letter or symbol when naming a function. The letters $f$, $g$,and $h$ are often used to represent functions. Sometimes we refer to the function relationship as a rule.

For example, to represent “height is a function of age,” we start by identifying variables for the domain and range. Let $a$ represent age and $h$ represent height. Next, define a name for the function. Let $f$ be the function name.

\[\begin{array}{ll} h \text{ is } f \text{ of }a \;\;\;\;\;\; & \text{We name the function }f \text{; height is a function of age.} \\ h=f(a) & \text{We use parentheses to indicate the function input.} \\ f(a) & \text{We name the function }f \text{ ; the expression is read as “ }f \text{ of }a \text{.”}\end{array}\nonumber\]

The notation $f(a)$ shows us that $h$ depends on $a$. The value $a$ must be put into the function $f$ to get an output $h$. The parentheses indicate that age is the input for the function; they do not indicate multiplication.

Note that the input and output of a function do not have to be numbers. They can be names of people, labels of geometric objects, etc. Most of the functions we will work with in this book will have numbers as inputs and outputs.

Function Notation

For the function $y=f(x)$

\[\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}\]

We read $f(x)$ as $f$ of $x$ or the value of $f$ at $x$.

We call x the independent variable as it can be any value in the domain. We call y the dependent variable as its value depends on x.

Example $\PageIndex{3}$

Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.

Solution

The number of days in a month is a function of the name of the month, so if we name the function $f$, we write $\text{days}=f(\text{month})$ or $d=f(m)$. The name of the month is the input to a “rule” that associates a specific number (the output) with each input.

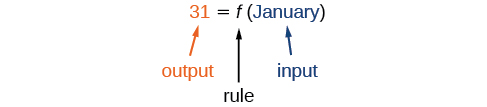
The function 31 = f(January) where 31 is the output, f is the rule, and January is the input. — Figure $\PageIndex{5}$: The function $31 = f(January)$ where 31 is the output, f is the rule, and January is the input.

For example, $f(\text{March})=31$, because March has 31 days. The notation $d=f(m)$ reminds us that the number of days, $d$ (the output), is dependent on the name of the month, $m$ (the input).

Analysis

Note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with in this book will have numbers as inputs and outputs.

Example $\PageIndex{4}$

A function $N=f(y)$ gives the number of police officers, $N$, in a town in year $y$. What does $f(2005)=300$ represent?

Solution

When we read $f(2005)=300$, we see that the input year is 2005. The value for the output, the number of police officers $(N)$, is 300. Remember, $N=f(y)$. The statement $f(2005)=300$ tells us that in the year 2005 there were 300 police officers in the town.

Q&A

Instead of a notation such as $y=f(x)$, could we use the same symbol for the output as for the function, such as $y=y(x)$, meaning “$y$ is a function of $x$?”

Yes, this is often done with formulas, especially in applied subjects that use higher level math, such as physics and engineering. While exploring math itself we like to maintain a distinction between a function such as $f$, which is a rule or procedure, and the output y we get by applying $f$ to a particular input $x$. This is why we usually use notation such as $y=f(x),P=W(d)$, and so on.

Evaluating a Function

When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.

Let's look at the function $y=4x−5$. To find the value of y when $x=2$, we know to substitute $x=2$ into the function and then simplify.

	$y=4x-5$
Let x=2.	$y=4\cdot 2-5$
	$y = 3 $

The value of the function at $x=2$ is 3.

We do the same thing using function notation, the equation $y=4x−5$ can be written as $f(x)=4x−5$. To find the value when $x=2$, we write:

	$f(x) = 4x-5$
Let x=2.	$f(2)=4 \cdot {\color{Red}2} -5 $
	$f(2) = 3 $

The value of the function at $x=2$ is 3.

This process of finding the value of $f(x)$ for a given value of x is called evaluating a function.

Example $\PageIndex{5}$

For the function $f(x)=2x^2+3x−1$, evaluate the function.

$f(3)$
$f(−2)$
$f(a)$

Solution

	$f(x)=2 x^2+3 x-1$
To evaluate $f(3)$, substitute 3 for x.	$f(3)=2(3)^2+3 \cdot 3-1$
Simplify.	$f(3)=2 \cdot 9+3 \cdot 3-1$
	$f(3)=18+9-1$
	$f(3)=26$

		$f(x) = 2$
To evaluate $f(-2)$, substitute $-2$ for $x$.		$f(-2)=2(-2)^2+3(-2)-1$
Simplify.		$f(-2)=2 \cdot 4+(-6)-1$
		$f(-2)=8+(-6)-1$
		$f(-2)=1$

	$f(x)=2 x^2+3 x-1$
To evaluate f(a),f(a), substitute a for x.	$f(x)=2 a^2+3 a-1$
Simplify.

You Try $\PageIndex{2}$

For the function $f(x)=3x^2−2x+1$, find the following:

$f(3)$
$f(−1)$
$f(t)$

Answer

a. $f(3)=22$

b. $f(−1)=6$

c. $f(t)=3t^2−2t+1$

Example $\PageIndex{6}$

For the function $g(x)=3x−5$, evaluate the function.

$g(h^2)$
$g(x+2)$
$g(x)+g(2)$

Solution

	$g(x)=3 x-5$
To evaluate $g(h^2)$, substitute $h^2$ for x.	$g\left(h^2\right)=3 h^2-5$
	$g\left(h^2\right)=3 h^2-5$

	$g(x)=3 x-5$
To evaluate $g(x+2)$, substitute $x+2$ for x.	$g(x+2)=3(x+2)-5$
Simplify.	$g(x+2)=3 x+6-5$
	$g(x+2)=3 x+1$

	$g(x)=3 x-5$
To evaluate $g(x)+g(2)$, first find $g(2)$.	$g(2)=3 \cdot 2-5$
	$g(2)=1$
	$g(x)+g(2)=\underbrace{3 x-5}_{g(x) \quad \quad g(2)}+1$
Simplify.	$g(x)+g(2)=3 x-5+1$
	$g(x)+g(2)=3 x-4$

Notice the difference between part b and c. We get $g(x+2)=3x+1$ and $g(x)+g(2)=3x−4$. So we see that $g(x+2)\neq g(x)+g(2)$.

You Try $\PageIndex{3}$

For the function $g(x)=4x−7$, evaluate the function.

$g(m^2)$
$g(x−3)$
$g(x)−g(3)$

Answer

a. $4m^2−7$

b. $4x−19$

c. $4x−12$

You Try $\PageIndex{4}$

Given the function $g(m)=\sqrt{m−4}$, evaluate

$g(5)$
$g(7)$

Answer

$g(5)=1$
$g(7)=\sqrt{3}$

Note: $\sqrt{3}$ is an irrational number. Since the directions did not indicate to approximate, we leave the answer in this form, called exact form, since irrational numbers are non-terminating non-repeating decimals. If the directions indicated to round to one decimal place, then we could state the answer as an approximatimation as, $g(7)\approx1.7$. Do remember to round appropriately.

Example $\PageIndex{7}$

Evaluate $f(x)=x^2+3x−4$ at

$2$
$a$
$a+h$
Evaluate $\frac{f(a+h)−f(a)}{h}$

Solution

Replace the x in the function with each specified value.

a. Because the input value is a number, 2, we can use simple algebra to simplify.

\[\begin{align*}f(2)&=2^2+3(2)−4\\&=4+6−4\\ &=6\end{align*}\]

b. In this case, the input value is a letter so we cannot simplify the answer any further.

\[f(a)=a^2+3a−4\nonumber\]

c. With an input value of $a+h$, we must use the distributive property.

\[\begin{align*}f(a+h)&=(a+h)^2+3(a+h)−4\\&=a^2+2ah+h^2+3a+3h−4 \end{align*}\]

d. In this case, we apply the input values to the function more than once, and then perform algebraic operations on the result. We already found that

\[f(a+h)=a^2+2ah+h^2+3a+3h−4\nonumber\]

and we know that

\[f(a)=a^2+3a−4 \nonumber\]

Now we combine the results and simplify.

\[\begin{align*}\dfrac{f(a+h)−f(a)}{h}&=\dfrac{(a^2+2ah+h^2+3a+3h−4)−(a^2+3a−4)}{h}\\ &=\dfrac{(2ah+h^2+3h)}{h} \\ &=\dfrac{h(2a+h+3)}{h} & &\text{Factor out h.}\\ &=2a+h+3 & & \text{Simplify.}\end{align*}\]

In the previous example, the formula in part d is called a difference quotient. In calculus, the difference quotient provides us with a way to describe instantaneous rate of change which is very useful.

Many everyday situations can also be modeled using functions. Let's look at an example.

You Try $\PageIndex{5}$

The number of unread emails in Sylvia’s account is 75. This number grows by 10 unread emails a day. The function $N(t)=75+10t$ represents the relation between the number of emails, N, and the time, t, measured in days.

Determine the independent and dependent variable.
Find $N(5)$. Explain what this result means.

Answer

a. The number of unread emails is a function of the number of days. The number of unread emails, N, depends on the number of days, t. Therefore, the variable N, is the dependent variable and the variable tt is the independent variable.

b. Find $N(5)$. Explain what this result means.

	$N(t)=75+10 t$
Substitute in t=5.t=5.	$N({\color{Red} 5})=75+10 \cdot {\color{Red} 5}$
Simplify.	$N(5)=75+50$
	$N(5)=125$

Since 5 is the number of days, $N(5)$, is the number of unread emails after 5 days. After 5 days, there are 125 unread emails in the account.

Finding Input Value(s) When Given an Output Value

When we know an output value and want to determine the input values that would produce the given output value, we set the output equal to the function’s formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.

Example $\PageIndex{8}$

Given the function $h(p)=p^2+2p$, solve for $h(p)=3$.

Solution

\[\begin{array}{rl} h(p)=3\\p^2+2p=3 & \text{Substitute the original function}\\ p^2+2p−3=0 & \text{Subtract 3 from each side.}\\(p+3)(p−1)=0&\text{Factor.}\end{array} \nonumber \]

If $(p+3)(p−1)=0$, either $(p+3)=0$ or $(p−1)=0$ (or both of them equal $0$). We will set each factor equal to $0$ and solve for $p$ in each case.

\[(p+3)=0,\; p=−3 \nonumber \]

\[(p−1)=0,\, p=1 \nonumber\]

This gives us two solutions. The output $h(p)=3$ when the input is either $p=1$ or $p=−3$. We can also verify by graphing as in Figure $\PageIndex{6}$. The graph verifies that $h(1)=h(−3)=3$ and $h(4)=24$.

[Graph of a parabola with labeled points (-3, 3), (1, 3), and (4, 24).] — Figure $\PageIndex{6}$: Graph of $h(p)=p^2+2p$

You Try $\PageIndex{6}$

Given the function $g(m)=\sqrt{m−4}$, solve $g(m)=2$.

Answer: $m=8$

Writing Equations as Functions

Some functions are defined by mathematical rules or procedures expressed in equation form. If it is possible to express the function output with a formula involving the input quantity, then we can write the equation using function notation. For example, the equation $2n+6p=12$ represents a functional relationship between $n$ and $p$. We can rewrite the equation as $p$ is a function of $n$ by solving the equation for $p$.

Example $\PageIndex{9}$

Express the relationship $2n+6p=12$ as a function $p=f(n)$

Solution

To express the relationship in this form, we need to write the relationship where $p$ is a function of $n$, which means writing it as $p=[\text{expression involving }n]$.

\[\begin{align*}2n+6p&=12 \\ 6p&=12−2n && \text{Subtract 2n from both sides.} \\ p&=\dfrac{12−2n}{6} & &\text{Divide both sides by 6 and simplify.} \\ p&=\frac{12}{6}−\frac{2n}{6} \\ p&=2−\frac{1}{3}n\end{align*}\]

Therefore, $p$ as a function of $n$ is written as

\[p=f(n)=2−\frac{1}{3}n \nonumber\]

Note: Not every relationship can be expressed using function notation. This can only be done when the equation represents a function.

Piecewise Defined Functions

Piecewise defined functions are used in many real-world phenomena (e.g. postal rates and income tax formulas) are modeled by such functions. It is important that we are familiar with them and know how to evaluate them.

Consider the absolute value function $f(x)=\left|x\right|$.

The domain is real numbers and the range is values greater than or equal to 0.

$f(x) = x$ if $x \ge 0$

If we input a negative value the sign of the output must change from negative to positive ($f(-1)=\left|-1\right|=1$, $f(-4.5)=\left|-4.5\right|=4.5$, ...).

$f(x) = -x$ if $x < 0$, since multiplying a negative value by -1 makes it positive.

Since this requires two different processes or pieces, the absolute value function is often called the most basic piecewise defined function.

Piecewise Function

A piecewise function is a function in which the formula used depends upon the domain the input lies in. We notate this idea like:

\[f(x) = \begin{cases} \text{formula 1, if domain value satisfies given criteria 1} \\ \text{formula 2, if domain value satisfies given criteria 2} \\ \text{formula 3, if domain value satisfies given criteria 3} \end{cases}\nonumber \]

Note that piecewise defined functions are not rescricted to 3 formulas, they may contain 2 or more.

Example $\PageIndex{10}$

A museum charges $5 per person for a guided tour with a group of 1 to 9 people, or a fixed $50 fee for 10 or more people in the group. Set up a function relating the number of people, $n$, to the cost, $C$.

Solution

To set up this function, two different formulas would be needed. C = 5n would work for n values under 10, and C = 50 would work for values of n ten or greater. Notating this:

\[C(n) = \begin{cases} 5n & \text{if 0 < n < 10} \\ 50 &\text{if } n \ge 10\end{cases}\nonumber \]

Example $\PageIndex{11}$

For the function $f(x)=\begin{cases}x+6, & \text{if }x<1\\ 3-x^2, &\text{if }x≥1\end{cases}$, find the following:

$f(0)$
$f(1)$
$f(3)$

Solution

Since the input is 0, we input into the top formula, $x+6$. So, $f(0)=0+6=6$
Since the input is 1, we input into the top formula, $x+6$. So, $f(1)=1+6=7$
Since the input is 3 we input into the bottom formula, $3-x^2$. So, $f(0)=0+6=6$

Example $\PageIndex{12}$

A cell phone company uses the function below to determine the cost, C, in dollars for g gigabytes of data transfer.

\[C(g)=\left\{\begin{array}{ccc} {25} & \text{if} & {0<g<2} \\ {25+10(g-2)} & \text{if} & {g\ge 2} \end{array}\right.\nonumber \]

Find the cost of using 1.5 gigabytes of data, and the cost of using 4 gigabytes of data.

Solution

To find the cost of using 1.5 gigabytes of data, $C(1.5)$, we first look to see which piece of domain our input falls in. Since 1.5 is less than 2, we use the first formula, giving $C(1.5)$ = $25.

The find the cost of using 4 gigabytes of data, $C(4)$, we see that our input of 4 is greater than 2, so we’ll use the second formula. $C(4)$ = 25 + 10(4 - 2) = $45.

Example $\PageIndex{13}$

The height $h$ in feet of a model rocket above the ground $t$ seconds after lift-off is given by

\[ h(t) = \left\{ \begin{array}{rcl} -5t^2 + 100t, & \mbox{if} & 0 \leq t \leq 20 \\ 0, & \mbox{if} & t > 20 \\ \end{array} \right.\nonumber\]

Find and interpret $h(10)$ and $h(60)$.
Solve $h(t) = 375$ and interpret your answers.

Solution

We first note that the independent variable here is $t$, chosen because it represents time. Secondly, the function is broken up into two rules: one formula for values of $t$ between $0$ and $20$ inclusive, and another for values of $t$ greater than 20. Since $t=10$ satisfies the inequality $0 \leq t \leq 20$, we use the first formula listed, $h(t) = -5t^2 + 100t$, to find $h(10)$. We get $h(10) = -5(10)^2 + 100(10) = 500$. Since $t$ represents the number of seconds since lift-off and $h(t)$ is the height above the ground in feet, the equation $h(10) = 500$ means that $10$ seconds after lift-off, the model rocket is $500$ feet above the ground. To find $h(60)$, we note that $t=60$ satisfies $t > 20$, so we use the rule $h(t) = 0$. This function returns a value of $0$ regardless of what value is substituted in for $t$, so $h(60) = 0$. This means that $60$ seconds after lift-off, the rocket is $0$ feet above the ground; in other words, a minute after lift-off, the rocket has already returned to Earth.
Since the function $h$ is defined in pieces, we need to solve $h(t) = 375$ in pieces. For $0 \leq t \leq 20$, $h(t) = -5t^2 + 100t$, so for these values of $t$, we solve $-5t^2 + 100t = 375$. Rearranging terms, we get $5t^2 - 100t + 375 = 0$, and factoring gives $5(t-5)(t-15) = 0$. Our answers are $t=5$ and $t=15$, and since both of these values of $t$ lie between $0$ and $20$, we keep both solutions. For $t>20$, $h(t) = 0$, and in this case, there are no solutions to $0=375$. In terms of the model rocket, solving $h(t) = 375$ corresponds to finding when, if ever, the rocket reaches $375$ feet above the ground. Our two answers, $t=5$ and $t=15$ correspond to the rocket reaching this altitude twice - once $5$ seconds after launch, and again $15$ seconds after launch.

Domain of Functions

We have learned that the domain of a function is the set of input values. How do find the domain when we are given a formula for a function?

First, let's recall some things from algebra.

If $f(x) = \frac{x}{x - 5}$, find $f(5)$. Evaluating this,

\[f(5) = \dfrac{(5)}{(5) - 5} = \dfrac{5}{0},\nonumber \]

which is undefined. Since the number $5$ makes the function undefined, this value is excluded from the domain. Since $5$ is the only real number that would make the denominator zero, the domain is $(-\infty, 5) \cup (5, \infty)$.

Next, If $g(x) = \sqrt{x + 3}$, find $g(-4)$. Evaluating this,

\[g(4) = \sqrt{(-4) + 3} = \sqrt{-1}\nonumber \]

which is not a real number.

Any real number that we input into this function that makes $x + 3$ negative must be excluded from the domain. So, the domain of this function is all real numbers such that $x + 3 \geq 0$ which yields $x \geq -3$. The domain in interval notation is $[-3, \infty)$.

When finding the domain of a function, we start with the set of all real numbers. Then, we exclude any values that make a denominator zero or result in an even root of a negative number.

How To Find the Domain of a Function

Identify the input values.
Identify any restrictions on the input and exclude those values from the domain. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for x . If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
Write the domain in interval notation.

Example $\PageIndex{14}$

Find the domain of the function $f(x)=x^2−1$.

Solution

The input value, shown by the variable x in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers.

In interval form, the domain of f is $(−\infty,\infty)$.

You Try $\PageIndex{7}$

Find the domain of the function:

\[f(x)=5−x+x^3 \nonumber\]

Answer: $(−\infty,\infty)$

Example $\PageIndex{15}$

Find the domain of the function $f(x)=\dfrac{x+1}{2−x}$.

Solution

When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for x.

\[ \begin{align*} 2−x=0 \\[4pt] −x &=−2 \\[4pt] x&=2 \end{align*}\]

Now, we will exclude 2 from the domain. The answers are all real numbers where $x<2$ or $x>2$. We can use a symbol known as the union, $\cup$,to combine the two sets. In interval notation, we write the solution:$(−\infty,2)∪(2,\infty)$.

$[Line graph of f(x).]$

In interval notation, the domain of f is $(−\infty,2)\cup(2,\infty)$.

You Try $\PageIndex{8}$

Find the domain of the function:

\[f(x)=\dfrac{1+4x}{2x−1} \nonumber\]

Answer: \[(−\infty,\dfrac{1}{2})\cup(\dfrac{1}{2},\infty) \nonumber\]

Example $\PageIndex{16}$

Find the domain of the function:

\[f(x)=\sqrt{7-x} \nonumber \]

Solution

When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand.

Set the radicand greater than or equal to zero and solve for x.

\[ \begin{align*} 7−x&≥0 \\[4pt] −x&≥−7\\[4pt] x&≤7 \end{align*}\]

Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to 7, or $\left(−\infty,7\right]$.

You Try $\PageIndex{9}$

Find the domain of the function

\[f(x)=\sqrt{5+2x}. \nonumber\]

Answer: \[\left[−2.5,\infty\right) \nonumber\]

Example $\PageIndex{17}$

Find the domain of the following functions. State answer in interval notation.

$g(x) = \sqrt{4 - 3x}$
$h(x) = \sqrt[5]{4 - 3x}$
$R(x) = \sqrt{x^2+5}$
$ F(x) = \dfrac{\sqrt[4]{2x+1}}{x^2 - 1}$
$r(t) = \dfrac{4}{6 - \sqrt{t+3}}$
$ I(p) = \dfrac{3p^2}{p}$

Solution

Set $4 - 3x \geq 0$. Solving this, we get $x \leq \frac{4}{3}$. This shows that as long as $x \leq \frac{4}{3}$, the radicand is greater than or equal to $0$, $4 - 3x \geq 0$, and the formula $g(x)$ outputs a real number. The domain is $\left(-\infty, \frac{4}{3}\right]$.
Although the formula for $h(x)$ is very similar to that of $g(x)$ there is one key difference: $g(x)$ is an even indexed root (namely a square root) and $h(x)$ is an odd indexed root (the fifth root). Since odd roots of real numbers (even negative real numbers) are real numbers, there is no restriction on the inputs to $h$. Hence, the domain is $(-\infty, \infty)$.
Since $x^2+5>0$ for all x, there is no restrictions on the inputs. Hence, the domain is $(-\infty, \infty)$.
There are two issues here: not only do we have a denominator, we have a fourth (even-indexed) root. We must determine the restrictions on each part and select the real numbers which satisfy both conditions. To satisfy the fourth root, $2x+1 \geq 0$. From this we get $x \geq -\frac{1}{2}$. Next, we find the values of $x$ which make the denominator equal to $0$, $x^2 - 1=0$. Solving this, $x = \pm 1$. Hence, in order for a real number $x$ to be in the domain of $F$, $x \geq -\frac{1}{2}$ but $x \neq \pm 1$. In interval notation, this set is $\left[ -\frac{1}{2}, 1 \right) \cup (1, \infty)$.
Don't be put off by the '$t$' here. It is an independent variable representing a real number, just like $x$ does, and is subject to the same restrictions. As in the previous problem, we have two issues here: we have a square root and a denominator. To satisfy the square root, we need a non-negative radicand so we set $t + 3 \geq 0$ to get $t \geq -3$. Setting the denominator equal to zero gives $6 - \sqrt{t+3} =0$, or $\sqrt{t+3} = 6$. Squaring both sides gives $t+3 = 36$, or $t = 33$. Remember that since we squared both sides in the course of solving this equation, we need to check our answer. Sure enough, when $t=33$, $6 - \sqrt{t+3} = 6 - \sqrt{36} = 0$, so $t=33$ will cause problems in the denominator. For the domain of $r$: we need $t \geq -3$, but $t \neq 33$. Hence, the domain is $[-3, 33) \cup (33, \infty)$.
It's tempting to simplify $I(x) = \frac{3x^2}{x} = 3x$. Since there are no longer any denominators it appears that the domain is $(-\infty, \infty)$ which is not the case. When simplifying $I(x)$, we are assuming $x \neq 0$, since $\frac{0}{0}$ is undefined. Proceeding as before, we find the domain of $I$ to be all real numbers except $0$: $(-\infty, 0) \cup (0, \infty)$.

It is worth reiterating the importance of finding the domain of a function before simplifying, as evidenced by the function $I$ in the previous example. Even though the formula $I(x)$ simplifies to $3x$, it would be inaccurate to write $I(x) = 3x$ without adding the stipulation that $x \neq 0$.

Example $\PageIndex{18}$

Find the domain of the function $v(t)=\sqrt{6-5t-t^{2} }$.

Solution

A square root is only defined when the quantity inside the square root, is zero or greater. Thus, the domain of this function will be when $6-5t-t^{2} \ge 0$. Solving this non-linear inequality yields $[-6, 1]$ which is the domain of the $v(t)$ function.

Example $\PageIndex{19}$

Given $g(x)=\dfrac{4+x}{x-3}$,

Find and simplify $g\left(\dfrac{1}{t}\right)$.
What is the domain of the function you found in part 1? State your answer in interval notation.

Solution

\[\begin{align*}g\left(\dfrac{1}{t}\right)&=\dfrac{4+\dfrac{1}{t}}{\dfrac{1}{t}-3}\\[4pt] &=\left(\dfrac{t}{t}\right)\left(\dfrac{4+\dfrac{1}{t}}{\dfrac{1}{t}-3}\right)\\[4pt] &=\dfrac{4t+1}{1-3t} \end{align*}\]
For $g\left(\dfrac{1}{t}\right) \text{ to be defined, } t\neq0$. In addition, for the function to be defined, $1-3t\neq0$. So, $t\neq\dfrac{1}{3}$.

The domain is $(-\infty,0) \cup \left(0,\dfrac{1}{3}\right) \cup \left(\dfrac{1}{3},\infty\right)$.

You Try $\PageIndex{10}$

Given $f(a)=\dfrac{3a}{a^2-7a+10} \text{ and } g(a)=\dfrac{2a}{a^2-8a+15}$,

Find and simplify $f(a)-g(a)$.
What is the domain of the function you found in part 1? State your answer in interval notation.

Answer

$\dfrac{a}{(a-3)(a-2)}$
$(-\infty,2) \cup (2,3) \cup (3,5) \cup (5,\infty)$

	\(y=4x-5\)
Let x=2.	\(y=4\cdot 2-5\)
	\(y = 3 \)

	\(f(x) = 4x-5\)
Let x=2.	\(f(2)=4 \cdot {\color{Red}2} -5 \)
	\(f(2) = 3 \)

	\(f(x)=2 x^2+3 x-1\)
To evaluate \(f(3)\), substitute 3 for x.	\(f(3)=2(3)^2+3 \cdot 3-1\)
Simplify.	\(f(3)=2 \cdot 9+3 \cdot 3-1\)
	\(f(3)=18+9-1\)
	\(f(3)=26\)

		\(f(x) = 2\)
To evaluate \(f(-2)\), substitute \(-2\) for \(x\).		\(f(-2)=2(-2)^2+3(-2)-1\)
Simplify.		\(f(-2)=2 \cdot 4+(-6)-1\)
		\(f(-2)=8+(-6)-1\)
		\(f(-2)=1\)

	\(g(x)=3 x-5\)
To evaluate \(g(h^2)\), substitute \(h^2\) for x.	\(g\left(h^2\right)=3 h^2-5\)
	\(g\left(h^2\right)=3 h^2-5\)

Search

Function

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

You Try \(\PageIndex{1}\)

Function Notation

Example \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Q&A

Example \(\PageIndex{5}\)

You Try \(\PageIndex{2}\)

Example \(\PageIndex{6}\)

You Try \(\PageIndex{3}\)

You Try \(\PageIndex{4}\)

Example \(\PageIndex{7}\)

You Try \(\PageIndex{5}\)

Example \(\PageIndex{8}\)

You Try \(\PageIndex{6}\)

Example \(\PageIndex{9}\)

Piecewise Function

Example \(\PageIndex{10}\)

Example \(\PageIndex{11}\)

Example \(\PageIndex{12}\)

Example \(\PageIndex{13}\)

How To Find the Domain of a Function

Example \(\PageIndex{14}\)

You Try \(\PageIndex{7}\)

Example \(\PageIndex{15}\)

You Try \(\PageIndex{8}\)

Example \(\PageIndex{16}\)

You Try \(\PageIndex{9}\)

Example \(\PageIndex{17}\)

Example \(\PageIndex{18}\)

Example \(\PageIndex{19}\)

You Try \(\PageIndex{10}\)

	\(f(x)=2 x^2+3 x-1\)
To evaluate f(a),f(a), substitute a for x.	\(f(x)=2 a^2+3 a-1\)
Simplify.

	\(g(x)=3 x-5\)
To evaluate \(g(x+2)\), substitute \(x+2\) for x.	\(g(x+2)=3(x+2)-5\)
Simplify.	\(g(x+2)=3 x+6-5\)
	\(g(x+2)=3 x+1\)

	\(g(x)=3 x-5\)
To evaluate \(g(x)+g(2)\), first find \(g(2)\).	\(g(2)=3 \cdot 2-5\)
	\(g(2)=1\)
	\(g(x)+g(2)=\underbrace{3 x-5}_{g(x) \quad \quad g(2)}+1\)
Simplify.	\(g(x)+g(2)=3 x-5+1\)
	\(g(x)+g(2)=3 x-4\)

	\(N(t)=75+10 t\)
Substitute in t=5.t=5.	\(N({\color{Red} 5})=75+10 \cdot {\color{Red} 5}\)
Simplify.	\(N(5)=75+50\)
	\(N(5)=125\)