2.5: Arcs, Angles, and Trig Function Values

Last updated
Save as PDF

Page ID: 69137

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

After studying this section, we should understand the concepts motivated by the questions below and be able to write precise, coherent answers to these questions:

How do we measure angles using degrees?
What do we mean by the radian measure of an angle? How is the radian measure of an angle related to the length of an arc on the unit circle?
Why is radian measure important?
How do we convert from radians to degrees and from degrees to radians?
How do we determine the values of both $x$ and $y$ when parameters on the domain are restricted?
What trigonometric functions are positive in the first, second, third and fourth quadrants?
How do we use one trigonometric function to represent or describe another?

The ancient civilization known as Babylonia was a cultural region based in southern Mesopotamia, which is present-day Iraq. Babylonia emerged as an independent state around 1894 BCE. The Babylonians developed a system of mathematics that was based on a sexigesimal (base 60) number system. This was the origin of the modern day usage of 60 minutes in an hour, 60 seconds in a minute, and 360 degrees in a circle.

Many historians now believe that for the ancient Babylonians, the year consisted of 360 days, which is not a bad approximation given the crudeness of the ancient astronomical tools. As a consequence, they divided the circle into 360 equal length arcs, which gave them a unit angle that was 1/360 of a circle or what we now know as a degree. Even though there are 365.24 days in a year, the Babylonian unit angle is still used as the basis for measuring angles in a circle. Figure $\PageIndex{1}$ shows a circle divided up into 6 angles of 60 degrees each, which is also something that fit nicely with the Babylonian base-60 number system.

$1.8.png$

Figure $\PageIndex{1}$: A circle with six 60-degree angles.

We often denote a line that is drawn through 2 points A and B by $\overleftrightarrow{AB}$. The portion of the line $\overleftrightarrow{AB}$ that starts at the point A and continues indefinitely in the direction point of point B is called ray AB and is denoted by $\overrightarrow{AB}$. The point A is the initial point of ray $\overrightarrow{AB}$. An angle is formed by rotating a ray about its endpoint. The ray in its initial position is called the initial side of the angle, and the position of the ray after it has been rotated is called the terminal side of the ray. The endpoint of the ray is called the vertex of the angle.

$1.9.png$

Figure $\PageIndex{2}$: An angle including some notation.

Figure $\PageIndex{2}$ shows the ray $\overrightarrow{AB}$ rotated about the point A to form an angle. The terminal side of the angle is the ray $\overrightarrow{AC}$. We often refer to this as angle BAC, which is abbreviated as $\angle{BAC}$. We can also refer to this angle as angle $CAB$ or $\angle{CAB}$. If we want to use a single letter for this angle, we often use a Greek letter such as $\alpha$(alpha). We then just say the angle ̨. Other Greek letters that are often used are $\beta$(beta), $\gamma$(gamma), $\theta$(theta), $\phi$(phi), and $\rho$(rho).

Arcs and Angles

To define the trigonometric functions in terms of angles, we will make a simple connection between angles and arcs by using the standard position of an angle. When the vertex of an angle is at the origin in the $xy$-plane and the initial side lies along the positive x-axis, we see that the angle is in standard position. The terminal side of the angle is then in one of the four quadrants or lies along one of the axes. When the terminal side is in one of the four quadrants, the terminal side determines the so-called quadrant designation of the angle. See Figure $\PageIndex{3}$.

$1.10.png$

Figure $\PageIndex{3}$: Standard position of an angle in the second quadrant.

Exercise $\PageIndex{1}$

Draw an angle in standard position in

the first quadrant;
the third quadrant; and
the fourth quadrant.

Answer

These graphs show positive angles in standard position. The one on the left has its terminal point in the first quadrant, the one in the middle has its terminal point in the third quadrant, and the one on the right has its terminal point in the fourth quadrant.

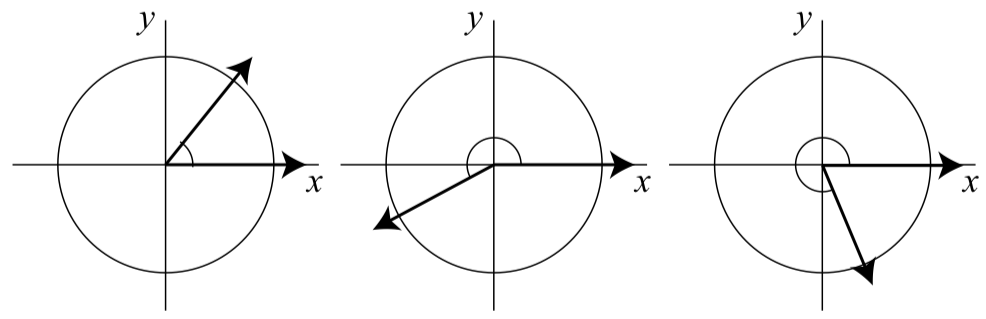
$1.13.png$

If an angle is in standard position, then the point where the terminal side of the angle intersects the unit circle marks the terminal point of an arc as shown in Figure 1.11. Similarly, the terminal point of an arc on the unit circle determines a ray through the origin and that point, which in turn defines an angle in standard position. In this case we say that the angle is subtended by the arc. So there is a natural correspondence between arcs on the unit circle and angles in standard position. Because of this correspondence, we can also define the trigonometric terminal side functions in terms of angles as well as arcs. Before we do this, however, we need to discuss two different ways to measure angles.

$1.11.png$

Figure $\PageIndex{4}$: An arc and its corresponding angle.

Degrees Versus Radians - A Review (Because we ALL need one!)

There are two ways we will measure angles – in degrees and radians. When we measure the length of an arc, the measurement has a dimension (the length, be it inches, centimeters, or something else). As mentioned in the introduction, the Babylonians divided the circle into 360 regions. So one complete wrap around a circle is 360 degrees, denoted $360^\circ$. The unit measure of $1^\circ$ is an angle that is 1/360 of the central angle of a circle. Figure $\PageIndex{1}$ shows 6 angles of $60^\circ$ each. The degree $^\circ$ is a dimension, just like a length. So to compare an angle measured in degrees to an arc measured with some kind of length, we need to connect the dimensions. We can do that with the radian measure of an angle.

Radians will be useful in that a radian is a dimensionless measurement. We want to connect angle measurements to arc measurements, and to do so we will directly define an angle of 1 radian to be an angle subtended by an arc of length 1 (the length of the radius) on the unit circle as shown in Figure $\PageIndex{5}$.

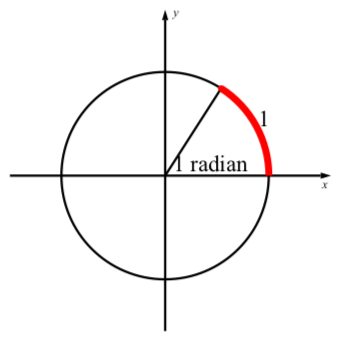
$1.12.png$

Figure $\PageIndex{5}$: One radian.

Definition: Radian

An angle of one radian is the angle in standard position on the unit circle that is subtended by an arc of length 1 (in the positive direction).

This directly connects angles measured in radians to arcs in that we associate a real number with both the arc and the angle. So an angle of 2 radians cuts off an arc of length 2 on the unit circle, an angle of 3 radians cuts of an arc of length 3 on the unit circle, and so on. Figure 1.13 shows the terminal sides of angles with measures of 0 radians, 1 radian, 2 radians, 3 radians, 4 radians, 5 radians, and 6 radians. Notice that $2\pi \approx 6.2832$ and so $6 < 2\pi$ as shown in Figure $\PageIndex{6}$.

$1.13.png$

Figure $\PageIndex{6}$: Angles with Radian Measure 1, 2, 3, 4, 5, and 6

We can also have angles whose radian measure is negative just like we have arcs with a negative length. The idea is simply to measure in the negative (clockwise) direction around the unit circle. So an angle whose measure is $-1$ radian is the angle in standard position on the unit circle that is subtended by an arc of length 1 in the negative (clockwise) direction.

So in general, an angle (in standard position) of $t$ radians will correspond to an arc of length $t$ on the unit circle. This allows us to discuss the sine and cosine of an angle measured in radians. That is, when we think of sin$(t)$ and cos$(t)$, we can consider $t$ to be:

a real number;
the length of an arc with initial point $(1, 0)$ on the unit circle;
the radian measure of an angle in standard position.

When we draw a picture of an angle in standard position, we often draw a small arc near the vertex from the initial side to the terminal side as shown in Figure $\PageIndex{7}$, which shows an angle whose measure is $\dfrac{3}{4}\pi$ radians.

Example $\PageIndex{1}$

1. Draw a terminal ray in the quadrant defined by the given $\theta$ restrictions; measuring from standard position with a radian measure:

Let $\sin({\theta}$

$\dfrac{\pi}{2}$
$\pi$ radians.
$\dfrac{3\pi}{2}$ radians.
$\dfrac{-3\pi}{2}$ radians.

2. What is the degree measure of each of the angles in part (1)?

Answer

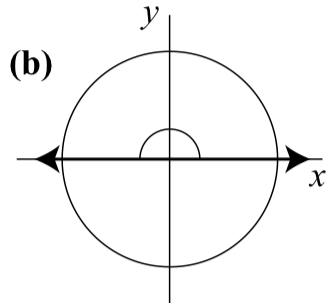
$1.14 b.png$ $1.14 c.png$ $1.14 d.png$

\[90^\circ\]
\[180^\circ\]
\[270^\circ\]
\[-270^\circ\]

Conversion Between Radians and Degrees

Radian measure is the preferred measure of angles in mathematics for many reasons, the main one being that a radian has no dimensions. However, to effectively use radians, we will want to be able to convert angle measurements between radians and degrees.

Recall that one wrap of the unit circle corresponds to an arc of length $2\pi$, and an arc of length $2\pi$ on the unit circle corresponds to an angle of $2\pi$ radians. An angle of $360^\circ$ is also an angle that wraps once around the unit circle, so an angle of $360^\circ$ is equivalent to an angle of $2\pi$ radians, or

each degree is $\dfrac{\pi}{180}$ radians,
each radian is $\dfrac{180}{\pi}$ degrees.

Notice that 1 radian is then $\dfrac{180}{\pi} \approx 57.3^\circ$, so a radian is quite large compared to a degree. These relationships allow us to quickly convert between degrees and radians.

Example $\PageIndex{1}$

If an angle has a degree measure of 35 degrees, then its radian measure can be calculated as follows:

\[35 \space degrees \times \dfrac{\pi \space radians}{180 \space degrees} = \dfrac{35\pi}{180} \space radians\]

Rewriting this fraction, we see that an angle with a measure of 35 degrees has a radian measure of $\dfrac{7\pi}{36}$ radians.

If an angle has a radian measure of $\dfrac{3\pi}{10}$ radians, then its degree measure can be calculated as follows:

\[\dfrac{3\pi}{10} \space radians \space \times \dfrac{180 \space degrees}{\pi \space radians}= \dfrac{540}{10} \space degrees\]

So an angle with a radian measure of $\dfrac{3\pi}{10}$ has an angle measure of 54$^\circ$.

IMPORTANT NOTE

Since a degree is a dimension, we MUST include the degree mark $^\circ$ whenever we write the degree measure of an angle. A radian has no dimension so there is no dimension mark to go along with it. Consequently, if we write 2 for the measure of an angle we understand that the angle is measured in radians. If we really mean an angle of 2 degrees, then we must write 2$^\circ$.

Exercise $\PageIndex{3}$

Complete the following table to convert from degrees to radians and vice versa.

Answer

Angle in Radians	Angle in degrees
$0$	$0^\circ$
$\dfrac{\pi}{6}$	$30^\circ$
$\dfrac{\pi}{4}$	$45^\circ$
$\dfrac{\pi}{3}$	$60^\circ$
$\dfrac{\pi}{2}$	$90^\circ$
$\dfrac{7\pi}{6}$	$210^\circ$
$\dfrac{5\pi}{4}$	$225^\circ$
$\dfrac{4\pi}{3}$	$240^\circ$
$\dfrac{3\pi}{2}$	$270^\circ$
$\dfrac{5\pi}{3}$	$300^\circ$
$\dfrac{2\pi}{3}$	$120^\circ$
$\dfrac{4\pi}{3}$	$135^\circ$
$\dfrac{5\pi}{6}$	$150^\circ$
$\pi$	$180^\circ$
$\dfrac{7\pi}{4}$	$315^\circ$
$\dfrac{11\pi}{6}$	$330^\circ$
$2\pi$	$360^\circ$

Calculators and the Trigonometric Functions

We have now seen that when we think of $\sin(t)$ or $\cos(t)$, we can think of $(t)$ as a real number, the length of an arc, or the radian measure of an angle. We will see how to determine the exact values of the cosine and sine functions for a few special arcs (or angles). For example, we will see that $\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2}$. However, the definition of cosine and sine as coordinates of points on the unit circle makes it difficult to find exact values for these functions except at very special arcs. While exact values are always best, technology plays an important role in allowing us to approximate the values of the circular (or trigonometric)functions. Most hand-held calculators, calculators in phone or tablet apps, and online calculators have a cosine key and a sine key that you can use to approximate values of these functions, but we must keep in mind that the calculator only provides an approximation of the value, not the exact value (except for a small collection of arcs). In addition, most calculators will approximate the sine and cosine of angles. Remember to read homework questions carefully - if it says anything about an exact number, it probably does NOT want a calculator approximation.

Angle in radians	Angle in degrees
0	$0^\circ$
$\dfrac{\pi}{6}$
$\dfrac{\pi}{4}$
$\dfrac{\pi}{3}$
$\dfrac{\pi}{2}$	$90^\circ$
	$120^\circ$
$\dfrac{3\pi}{4}$	$135^\circ$
	$150^\circ$
	$180^\circ$
$\dfrac{7\pi}{6}$
$\dfrac{5\pi}{4}$
$\dfrac{4\pi}{3}$
$\dfrac{3\pi}{2}$	$270^\circ$
	$300^\circ$
	$315^\circ$
	$330^\circ$
$2\pi$	$360^\circ$

Table 1.1: Conversions between radians and degrees.

To do this, the calculator has two modes for angles: Radian and Degree. Because of the correspondence between real numbers, length of arcs, and radian measures of angles, for now, we will always put our calculators in radian mode. In fact, we have seen that an angle measured in radians subtends an arc of that radian measure along the unit circle. So the cosine or sine of an angle measure in radians is the same thing as the cosine or sine of a real number when that real number is interpreted as the length of an arc along the unit circle. (When we study the trigonometry of triangles, we will use the degree mode. In general, if a questions or application is given in degrees the solution is usually also given in degrees. Similarly, when working in radians the solution would also be given in radians, unless you have specifically been asked to convert from one to the other form.

Exercise $\PageIndex{4}$

We can use the Geogebra Applet called Terminal Points of Arcs on the Unit Circle at http://gvsu.edu/s/JY to approximate the values of the cosine and sine functions at certain values. For example, we could find the following:

$\cos(1) \approx 0.5403$, $\sin(1) \approx 0.8415$.
$\cos(2) \approx -0.4161$, $\sin(2) \approx 0.9093$.
$\cos(-4) \approx -0.6536$, $\sin(-4) \approx 0.7568$.
$\cos(-15) \approx -0.7597$, $\sin(-15) \approx -0.6503$.

Use a calculator to determine these values of the cosine and sine functions and compare the values to the ones above. Are they the same? How are they different?

Answer

Using a calculator, we obtain the following results correct to ten decimal places:

$\cos(1) \approx 0.5403023059, \sin(1) \approx 0.8414709848$. $\cos(1) \approx 0:4161468365, \sin(1) \approx 0.9092974268$.

The difference between these values and those obtained previously, is that these values are correct to 10 decimal places (and the others are correct to 4 decimal places). If we round off each of the values above to 4 decimal places, we get the same results.

$\cos(1) \approx 0:6536436209, \sin(1) \approx 0.7568024953$.
$\cos(1) \approx 0:7596879129, \sin(1) \approx 0.6502878402$.

Exercise $\PageIndex{5}$

When working with sine and cosine we are reminded that these two functions can be used to generate the remaining 4 functions - tangent, secant, cosecant and cotangent.

Each of these trigonometric functions are positive in different quadrants of the unit circle. Now that we can calculate the values of sine and cosine at ANY terminal point along a unit circle, we now need to be able to do the same for the remaining 4 functions.

In quadrant I ALL trigonometric functions are positive.
In quadrant II the SINE function is positive.
In quadrant III the TANGENT function is positive.
In quadrant IV the COSINE function is positive.

Using the first letter from each of these quadrants and putting it into an easy-to-remember phrase can help you remember where functions are positive.

Here are some common phrases: "All Students Take Calculus" "A Smart Trig Class" or maybe you can think up a better one!

In what quadrant does the terminal ray reside if $sin(t)<0$ and $cos(t)<0$?
In what quadrant does the terminal ray reside if $tan(t)<0$ and $cos(t)>0$?
In what quadrant does the terminal ray reside if $sec(t)<0$ and $tan(t)>0$?
In what quadrant does the terminal ray reside if $csc(t)>0$ and $cot(t)<0$?

Answer

Sine is negative in quadrant III and IV, while cosine is negative in quadrant II and III. Therefore the overlap must be in quadrant II where both functions are negative.
Recall that tangent has an identity where $tan(t)=\dfrac{sin(t)}{cos(t)}$ is negative in quadrant II and IV, while cosine is positive in quadrant I and IV. Therefore the overlap must be in quadrant IV where these parameters are both met.
Recall that secant has an identity where $sec(t)=\dfrac{1}{cos(t)}$ this implies that the same quadrants will be positive for secant as for cosine. Secant is negative in quadrants II and III, while tangent is positive in quadrant I and III. Therefore the overlap must be in quadrant III where these parameters are both met.
Recall that cosecant has an identity where $csc(t)=\dfrac{1}{sin(t)}$ this implies that the same quadrants will be positive for cosecant as for sine. Recall that cotangent is the reciprocal of tangent and has an identity where $cot(t)=\dfrac{cos(t)}{sin(t)}$ is negative in quadrant II and IV. Cosecant is positive in quadrants I and II, while cotangent is negative in quadrant II and IV. Therefore, the overlap must be in quadrant II where these parameters are both met.

Exercise $\PageIndex{6}$

Sometimes it will be important to write a given trigonometric function in terms of another.

The Pythagorean Theorem is $sin^2(\theta)$+$cos^2(\theta)$=1.

Dividing this initial identity by $sin^2(\theta)$ will generate another form for Pythagorean Theorem.

Dividing this initial identity by $cos^2(\theta)$ will generate a third form.

Use these three different forms to find the functions listed in terms of another function. Use the quadrant to determine if the function is positive or negative.

Remember from the previous exercise that the following are true:

In quadrant I ALL trigonometric functions are positive.
In quadrant II the SINE function is positive.
In quadrant III the TANGENT function is positive.
In quadrant IV the COSINE function is positive.

Use the Pythagorean Theorem and the phrase you have memorized to find the following trigonometric functions:

Write the $tan\theta$ in terms of $cos\theta$ for $\theta$ in Quadrant II.
Write the $sin\theta$ in terms of $cos\theta$ for $\theta$ in Quadrant III.
Write the $tan\theta$ in terms of $sec\theta$ for $\theta$ in Quadrant I.
Write the $sec\theta$ in terms of $cos\theta$ for $\theta$ in Quadrant IV.

Answer

We need to find a way to write $tan\theta$ equal to something on the right with only cosine functions included. If we divide $sin^2\theta$+$cos^2\theta$=1 by $cos^2\theta$ we will have a form for the Pythagorean Theorem in terms of tangent and cosine. \[\dfrac{sin^2\theta}{cos^2\theta}+\dfrac{cos^2\theta}{cos^2\theta}=\dfrac{1}{cos^2\theta}\] Now, solving for tangent we should have: \[tan^2\theta=\dfrac{1}{cos^2\theta}-\dfrac{cos^2\theta}{cos^2\theta}\] Simplify and take the square root of both sides. Remember, tangent is negative in Quadrant II, therefore our answer should be: \[tan\theta=-\dfrac{\sqrt{1-cos^2 \theta} }{cos\theta }\]
\[sin\theta=- \sqrt{1-cos^2\theta} \]
\[tan\theta= \sqrt{sec^2\theta-1} \]
\[tan\theta=-\dfrac{1}{ \sqrt{1-cos^2 \theta } }\]

Exercise $\PageIndex{7}$

Throughout trigonometry - even in Calculus, Linear Algebra and some Differential Equations classes - we will be asked to find the terminal point given limited information and sometimes restrictions on your domain or quadrant. Use the Pythagorean Theorem to find the missing sides and recognize when the function will be positive or negative based on the quadrant. It is usually helpful to first restrict the quadrant to the one in which the values are true, then calculate the exact value for the remaining five functions based on the given information.

Given $sin\theta=-\dfrac{4}{5}$ find the remaining five values for the remaining five functions if $\theta$ is in Quadrant IV.
Given $cos\theta=-\dfrac{5}{6}$ find the remaining five values for the remaining five functions if $cot\theta>0$.
Given $csc\theta=3$ find the remaining five values for the remaining five functions in Quadrant I.
Given $cos\theta=\dfrac{7}{13}$ find the remaining five values for the remaining five functions if $sin\theta<0$.
Given $sec\theta=-\dfrac{1}{2}$ find the remaining five values for the remaining five functions if $csc\theta<0$.
Given $cos\theta=-\dfrac{2}{11}$ find the remaining five values for the remaining five functions if$tan\theta<0$.

Answer

Rotating through to a terminal ray in Quadrant IV, we now can draw a triangle using the terminal ray as the hypotenuse of the triangle. Use a reference angle off the x axis to orient the opposite and adjacent sides. The missing side is the x-direction length. Using the Pythagorean Theorem the sides of the triangle should be: Opposite is -4, Adjacent is 3 and Hypotenuse is 5. Now, using the identities, \[sin\theta=\dfrac{opposite}{hypotenuse}=\dfrac{-4}{5}\] \[cos\theta=\dfrac{adjacent}{hypotenuse}=\dfrac{3}{5}\] and \[tan\theta=\dfrac{opposite}{adjacent}=\dfrac{sin\theta}{cos\theta}=\dfrac{-4}{3}\] For the remaining three trig functions we can use what we found previously, just as reciprocals: \[csc\theta=\dfrac{hypotenuse}{opposite}=\dfrac{5}{-4}\] \[sec\theta=\dfrac{hypotenuse}{adjacent}=\dfrac{5}{3}\] \[cot\theta=\dfrac{adjacent}{opposite}=\dfrac{cos\theta}{sin\theta}=\dfrac{3}{-4}\] NOTE:From here on the answers will be simplified such that we bring the negative sign in front of the fraction and it is understood that it was associated with the negative side of the triangle. It is more formal to write it in front of the fraction instead of with the numerator or denominator.
Cotangent is only positive in Quadrants I and III. While Cosine is only negative in Quadrants II and III. Therefore, we know our values for all six trig functions must exist in Quadrant III! \[sin\theta=\dfrac{opposite}{hypotenuse}=-\dfrac{\sqrt{11}}{6}\] \[cos\theta=-\dfrac{5}{6}\] \[tan\theta=\dfrac{opposite}{adjacent}=\dfrac{sin\theta}{cos\theta}=\dfrac{\sqrt{11}}{5}\] For the remaining three trig functions we can use what we found previously, just as reciprocals:\[csc\theta=\dfrac{hypotenuse}{opposite}=-\dfrac{6\sqrt{11}}{11}\] \[sec\theta=\dfrac{hypotenuse}{adjacent}=-\dfrac{6}{5}\] \[cot\theta=\dfrac{adjacent}{opposite}=\dfrac{cos\theta}{sin\theta}=\dfrac{5\sqrt{11}}{11}\]
\[sin\theta=\dfrac{1}{3}\] \[cos\theta=\dfrac{2\sqrt{2}}{3}\] \[tan\theta=\dfrac{\sqrt{2}}{4}\] \[csc\theta=3\] \[sec\theta=\dfrac{3\sqrt{2}}{4}\] \[cot\theta=2\sqrt{2}\]
\[sin\theta=-\dfrac{2\sqrt{30}}{13}\] \[cos\theta=\dfrac{7}{13}\] \[tan\theta=2\dfrac{2\sqrt{30}}{7}\] \[csc\theta=-\dfrac{13\sqrt{30}}{60}\] \[sec\theta=\dfrac{13}{7}\] \[cot\theta=-\dfrac{7\sqrt{30}}{60}\]
Algebraically, we can calculate the value of cosine because $sec\theta=-\dfrac{1}{2}$. Therefore, cosine is -2. If we try to calculate the values for the remaining 5 functions we notice that the hypotenuse is less than the adjacent side. This should be a warning sign that the values do not exist. Geometrically/Graphically, we could plot or graph the function $f(x)=sec\theta$ simultaneously with $f(x)=-\dfrac{1}{2}$ to see that there is never a point at which the two functions intersect. This should lead us to believe that there is NO SOLUTION, or a solution DOES NOT EXIST (sometimes annotated as DNE).
\[sin\theta=\dfrac{3\sqrt{13}}{11}\] \[cos\theta=-\dfrac{2}{1}\] \[tan\theta=-\dfrac{3\sqrt{13}}{2}\] \[csc\theta=\dfrac{11\sqrt{13}}{39}\] \[sec\theta=-\dfrac{11}{2}\] \[cot\theta=-\dfrac{2\sqrt{13}}{39}\]

Section Summary

In this section, we studied the following important concepts and ideas:

An angle is formed by rotating a ray about its endpoint. The ray in its initial position is called the initial side of the angle, and the position of the ray after it has been rotated is called the terminal side of the ray. The endpoint of the ray is called the vertex of the angle.
When the vertex of an angle is at the origin in the $xy$-plane and the initial side lies along the positive x-axis, we see that the angle is in standard position.
There are two ways to measure angles. For degree measure, one complete wrap around a circle is 360 degrees, denoted 360$^\circ$. The unit measure of 1$^\circ$ is an angle that is 1=360 of the central angle of a circle. An angle of one radian is the angle in standard position on the unit circle that is subtended by an arc of length 1 (in the positive direction).
We convert the measure of an angle from degrees to radians by using the fact that each degree is radians. We convert the measure of an angle from 180 radians to degrees by using the fact that each radian is 180 degrees.
We looked at the strategies to use when finding the range values for all 6 trigonometric functions.
We imposed restriction on the domain and quadrant, then found the missing trig function value. This will come in handy in the following sections!

Angle in Radians	Angle in degrees
\(0\)	\(0^\circ\)
\(\dfrac{\pi}{6}\)	\(30^\circ\)
\(\dfrac{\pi}{4}\)	\(45^\circ\)
\(\dfrac{\pi}{3}\)	\(60^\circ\)
\(\dfrac{\pi}{2}\)	\(90^\circ\)
\(\dfrac{7\pi}{6}\)	\(210^\circ\)
\(\dfrac{5\pi}{4}\)	\(225^\circ\)
\(\dfrac{4\pi}{3}\)	\(240^\circ\)
\(\dfrac{3\pi}{2}\)	\(270^\circ\)
\(\dfrac{5\pi}{3}\)	\(300^\circ\)
\(\dfrac{2\pi}{3}\)	\(120^\circ\)
\(\dfrac{4\pi}{3}\)	\(135^\circ\)
\(\dfrac{5\pi}{6}\)	\(150^\circ\)
\(\pi\)	\(180^\circ\)
\(\dfrac{7\pi}{4}\)	\(315^\circ\)
\(\dfrac{11\pi}{6}\)	\(330^\circ\)
\(2\pi\)	\(360^\circ\)

Angle in radians	Angle in degrees
0	\(0^\circ\)
\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{\pi}{2}\)	\(90^\circ\)
	\(120^\circ\)
\(\dfrac{3\pi}{4}\)	\(135^\circ\)
	\(150^\circ\)
	\(180^\circ\)
\(\dfrac{7\pi}{6}\)
\(\dfrac{5\pi}{4}\)
\(\dfrac{4\pi}{3}\)
\(\dfrac{3\pi}{2}\)	\(270^\circ\)
	\(300^\circ\)
	\(315^\circ\)
	\(330^\circ\)
\(2\pi\)	\(360^\circ\)