1.1: Integers
- Page ID
- 104794
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
By the end of this section, you will be able to:
- Add and subtract integers
- Multiply and divide integers
- Simplify expressions with absolute value
Natural Numbers and Integers
Let's begin by reviewing some numbers. We are all familiar with the counting numbers, or as mathematicians say, natural numbers \(\mathbb{N}\). These are \(0, 1,2,\ldots, 51,\ldots, 1000000,\ldots\)
We can see these numbers on what is called a number line. Here is the number line with the natural numbers going from 0 to 5. The numbers are ascending going from left to right and descending from right to left. Larger numbers are to the right and smaller numbers are to the left.
We can add them together to get another natural number.
Compute the following:
- 1+2=
- 3+5=
- 43 + 27=
- 900+716=
- Answer
-
- 1+2=3
- 3+5=8
- 43 + 27 = 70
- 900+716=1616
We say the result of addition is the sum For example, the sum of 1 and 2 is 3. (The sum is 3, not 1 or 2).
We can also come up with numbers that add up to a certain number.
Come up with two natural numbers whose sum is 7.
- Possible answers:
-
6 and 1
5 and 2
4 and 3
7 and 0
Any other combinations would be a repeat of those above.
What if we want to subtract? Sometimes we run into a new kind of number. For example 5-7=-2. This is a negative number and they were invented to keep track of debts. For example if you have 5 dollars and you need to pay me 7 dollars then you have -2 dollars, that is, you are 2 dollars in debt to me, the book.
You can actually think of subtraction as adding a negative, e.g, 5+(-7)=-2. So you really never lose money, you just get a negative money!
We can expand our view of numbers to include negative numbers to define the integers, \(\mathbb{Z}\), by \(\ldots,-1000000,\ldots, -51,\ldots, -2,-1,0,1,2,\ldots, 51\ldots, 1000000,\ldots\). That is, the integers are the negative AND positive versions of the natural numbers combined.
We also say that the result of subtraction is the difference. For example, the difference between 5 and 2 is 3. (The difference is 3, not 5 or 2).
Let's expand the number line to include the negatives. Again, larger numbers are to the right and smaller numbers are to the left.
Addition and subtraction may be easier to see with a number line. On a number line we go to the right for adding a positive number and to when adding a negative (subtraction).
Consider -4+8=4. On a number line, this looks like

We start at -4 and then move 8 numbers to the right (because we are adding 8), landing at 4.
We can do the same for subtraction.
For example, let's do -3-4=-7

Now we start at -3 and move 4 numbers to the left (because we are subtracting 4), landing at -7.
With this in mind, let's try some examples.
Compute the following:
- 5-2=
- 7-5=
- 5-10=
- -10+5=
- -7+4=
- Answer
-
- 5-2=3
- 7-5=2
- 5-10=-5
- -10+5=-5
- -7+4=-3
We see that there is a relationship between addition and subtraction in the sense that one "undoes" the other. For example
\[
1+2=3\\
1=3-2\\
\]
We see that the action of adding 2 to 1 to get 3 can be "undone" by subtracting 2 from 3.
Multiply and Divide Integers
Often in math and life, we would like to add quickly. Say you had 4 boxes with 3 phones in each box and I ask "how many phones do you have"? You could use addition with 3+3+3+3=12 or you could use multiplication with \(3\cdot 4=12\). So one could think of multiplication as adding the same number to itself in a succinct way. Multiplication is very useful when numbers get too inconvenient to add. For example, let's say you have 100 boxes now. It would be difficult to add up all those 3's but with multiplication we know that \(3\cdot 100=300\). We call the result of multiplication, the "product". For example, the product of 3 and 100 is 300. (300 is the product, not 3 or 100).
- \(1\cdot 2\)
- \(5\cdot 6\)
- \(3\cdot 9\)
- \(12\cdot 54\)
- Come up with two integers whose product is 6.
- Answer
-
- 2
- 30
- 27
- 648
- An answer is \(2\cdot 3\)
What if we want to do multiplication with negative numbers? An intuitive way of understanding multiplication with negative numbers is to consider debts again. Say you owe 3 dollars to 4 people, how much are you in debt? The answer is 12 dollars in debt. In math terms, this is \(4\cdot (-3)=-12\). So a positive number multiplied by a negative number is a negative number. (A negative number multiplied by a positive number is a negative number).
What about a negative number multiplied by a negative number? To understand this, let's consider an "I owe you" note. This note is a physical interpretation of debt or "negative money". If Tom has a note that reads "Tom owes (your name) 3 dollars" this means that Tom is in debt to you by the amount of 3 dollars. Ok, now let's say that you needs to give Tom 4 copies of the note above, we can say that you owe Tom those notes. How much money would you have if everyone paid off their debt? Well, each note reads "Tom owes (your name) 3 dollars" and you gives Tom 4 of those notes, then you will have 12 dollars once the debt is paid off. In math terms we have -4 (notes that you owes Tom) \(\cdot -3\) (The amount of negative money each note carries)=12. That is to say "if you owe someone negative money then you are owed positive money". So a negative times a negative is a positive!
This also answers the question about why 4-(-3)=7. Since you can think of the subtraction of negative 3 as giving one of the notes above.
Division is a way of...dividing up a number into another number. To get an intuitive understanding let's consider some pizza. Let's say that your friends eat 2 slices of pizza each and you have a pizza with 8 slices. How many of your friends can you feed with that pizza? This question is asking to divide 8 (slices of pizza) by 2 (the amount of slices each friend will eat). So \(8\div 2=4\), you will be able to feed 4 friends with 1 pizza. We call the result of division, the "quotient". For example, the quotient of 8 by 2 is 4. (4 is the quotient, not 8 or 2). We see the same intuition with negative numbers works for division as well. That is, if you need to divide a debt of 6 dollars between 3 people evenly then each person would owe you 2 dollars: \(\frac{-6}{-3}=2\). Same intuition holds if you need to pay off a 6 dollar debt between 3 people evenly: \(\frac{-6}{3}=-2\).
- \(2\div 2=\)
- \(30\div 6=\)
- \(-27\div 9=\)
- \(-16\div -8=\)
- \(648\div 54=\)
- Answer
-
- 1
- 5
- -3
- 2
- 12
To recap
For multiplication and division of two signed numbers:
| Same signs | Result |
|---|---|
| • Two positives | Positive |
| • Two negatives | Positive |
If the signs are the same, the result is positive.
| Different signs | Result |
|---|---|
| • Positive and negative | Negative |
| • Negative and positive | Negative |
If the signs are different, the result is negative.
Sometimes we encounter a division that we can't get an integer out of. Say you have one slice of pizza and eat friend eats 2 slices. How many friends can you feed? You can feed half of a friend. In math this would look like this \(\frac{1}{2}\). These are called fractions and we will be talking about them in the next section but first we should talk about when we do get an integer from division.
Simplify Expressions with Absolute Value
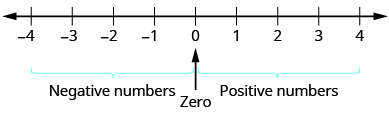
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers \(2\) and \(−2\) are the same distance from zero, each one is called the opposite of the other. The opposite of \(2\) is \(−2\), and the opposite of \(−2\) is \(2\).
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
This figure \(\PageIndex{2}\) illustrates the definition.

Figure \(\PageIndex{2}\). The opposite of 3 is \(−3\).
\[\begin{align} & -a \text{ means the opposite of the number }a \\ & \text{The notation} -a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
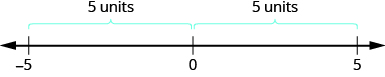
We saw that numbers such as 3 and −3 are opposites because they are the same distance from 0 on the number line. They are both three units from 0. The distance between 0 and any number on the number line is called the absolute value of that number.
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number \(n\) is written as \(|n|\) and \(|n|≥0\) for all numbers.
Absolute values are always greater than or equal to zero.
For example,
\[\begin{align} & -5 \text{ is } 5 \text{ units away from 0, so } |-5|=5. \\ & 5 \text{ is }5\text{ units away from 0, so }|5|=5. \end{align}\]
Figure \(\PageIndex{3}\) illustrates this idea.
The absolute value of a number is never negative because distance cannot be negative. The only number with absolute value equal to zero is the number zero itself because the distance from 0 to 0 on the number line is zero units.
In the next example, we’ll order expressions with absolute values.
Fill in \(<,\,>,\) or \(=\) for each of the following pairs of numbers:
- \(\mathrm{|-5|}\,\_\_\,\mathrm{-|-5|}\)
- \(8\_\_−|−8|\)
- \(−9\_\_−|−9|\)
- \(−(−16)\_\_|−16|\).
- Answer
-
- First, simplify each side:
\( |-5| = 5 \text { and } -|-5| = -5\)
Then choose an inequality that makes the simplified statement true:
\( 5 > -5\)
This is the inequality that makes the original statement true!
\(|-5| > -|-5|\)
- First, simplify each side:
The left side is already simplified. The right side simplifies as \( -|-8| = -8\)
Then choose an inequality that makes the simplified statement true:
\( 8 > -8\)
This is the inequality that makes the original statement true!
\(8 > -|-8|\)
- First, simplify each side:
The left side is already simplified. The right side simplifies as \( -|-9| = -9\)
Then choose an inequality (or equality!) that makes the simplified statement true:
\( -9 = -9\)
This is the inequality or equality that makes the original statement true!
\(-9 = -|-9|\)
- First, simplify each side:
\( -(-16) = 16 \text { and } |-16| = 16\)
Then choose an inequality (or equality!) that makes the simplified statement true:
\( 16 = 16\)
This is the inequality or equality that makes the original statement true!
\(-(-16) > |-16|\)
- First, simplify each side:
Fill in \(<,\,>,\) or \(=\) for each of the following pairs of numbers:
- \(−9 \_\_−|−9|\)
- \(2 \_\_−|−2|\)
- \(−8 \_\_|−8|\)
- \(−(−9) \_\_|−9|\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(=\)
Order of Addition and Multiplication
If we want to compute \(2+3\cdot 2\) is this 10 or 8? It's ambiguous which operation we want to do first so mathematicians have some rules of which operations we do first. In order we do multiplication, division, addition, and finally subtraction. We will have exceptions like if the addition is inside parenthesis, like \((2+3)\cdot 2\), in this case, it would be 10. Expressions in parenthesis (or any grouping symbols) take priority.
We now add absolute value bars to our list of grouping symbols. When we use the order of operations, first we simplify inside the absolute value bars as much as possible, then we take the absolute value of the resulting number.
\[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
In the next example, we simplify the expressions inside absolute value bars first just like we do with parentheses.
Simplify: \(\mathrm{24−|19−3(6−2)|}\).
- Answer
-
Work inside parentheses first -- subtract 2 from 6: \(24−|19−3(4)|\)
Simplify the multiplication inside the absolute value next: \(24−|19−12|\)
Simplify the inside of the absolute value bars -- subtract 12 from 19: \(24−|7|\)
Take the absolute value: \(24 - 7\)
Subtract: \(17\)
Simplify: \(19−|11−4(3−1)|\).
- Answer
-
16
Work inside parentheses first -- subtract 1 from 3: \(19−|11−4(2)|\)
Simplify the multiplication inside the absolute value next: \(19−|11−8|\)
Simplify the inside of the absolute value bars -- subtract 8 from 11: \(19−|3|\)
Take the absolute value: \(19 - 3\)
Subtract: \(16\)
Simplify: \(9−|8−4(7−5)|\).
- Answer
-
9
Key Concepts
- Numberlines help visualize addition and subtraction.
- The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as \(|n|\) and \(|n|≥0\) for all numbers.
Absolute values are always greater than or equal to zero.
- \[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
- Subtraction Property
\(a−b=a+(−b)\)
Subtracting a number is the same as adding its negative. - For multiplication and division of two signed numbers:
If the signs are the same, the result is positive.Multiplication and division for two same signed numbers Same signs Result • Two positives Positive • Two negatives Positive
If the signs are different, the result is negative.Multiplication and division for two different signed numbers Different signs Result • Positive and negative Negative • Negative and positive Negative - Multiplication by \(−1\)
\(−1a=−a\)
Multiplying a number by \(−1\) gives its opposite.
Glossary
- absolute value
- The absolute value of a number is its distance from \(0\) on the number line.
- integers
- The whole numbers and their opposites are called the integers.
- negative numbers
- Numbers less than \(0\) are negative numbers.

