1.2: Fractions
- Page ID
- 104796
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Simplify fractions
- Multiply and divide fractions
- Add and subtract fractions
- Use the order of operations to simplify fractions
Compute the following
- \(16\div 2\)
- \(-16\div -8\)
- \(6\div -6\)
- Answer
-
- 8
- 2
- -1
What is a Fraction?
Now try \(1\div 2\). Is this an integer? No, it's just \(1\div 2\)
Conceptually this is asking how many friends you can feed with 1 slice of pizza if each friend eats 2 slices. Well, you can feed half of a friend, that is \(\frac{1}{2}\). If we expand our numbers once again we can accommodate these new numbers we will call fractions. Fractions represent smaller parts of whole numbers. If we now allow fractions, we get the rationals, \(\mathbb{Q}\). Rationals are any number that can be written as an integer over an integer.
A fraction is written \(\dfrac{a}{b}\), where \(b\neq 0\) and
\(a\) is the numerator and \(b\) is the denominator.
A fraction represents parts of a whole. The denominator \(b\) is the number of equal parts the whole has been divided into, and the numerator \(a\) indicates how many parts are included.
Let's create a fraction for example, take a random integer.
7? Good choice! Take another integer.
3? Another good choice!Taking 7 over 3 we get \(\frac{7}{3}\). Really this is expressing the number we get when we divide 7 by 3.
Where does the negative sign go in a fraction? Usually the negative sign is in front of the fraction, but you will sometimes see a fraction with a negative numerator, or sometimes with a negative denominator. Remember that fractions represent division. When the numerator and denominator have different signs, the quotient is negative.
\[\dfrac{−1}{3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{negative}}{\text{positive}}=\text{negative}\]
\[\dfrac{1}{−3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{positive}}{\text{negative}}=\text{negative}\]
For any positive numbers \(a\) and \(b\),
\[\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\]
If we have -7 or -3 but not both then we would get \(-\frac{7}{3}\) This is the same as \(\frac{-7}{3}\) or \(\frac{7}{-3}\).
\(\frac{-7}{3} = \frac{7}{-3} = -\frac{7}{3}\)
Any integer can be turned into a fraction with 1 as the denominator e.g \(3=\frac{3}{1}\).
Let's take a look at when we will get a nice integer from division.
Factor Trees
A number \(x\) is "divisible" by another number \(y\) if \(x\div y\) is an integer
9 is divisible by 3 since \(9\div 3=3\)
9 is not divisible by 2 since \(9\div 2\) is not an integer.
A "prime number" is an integer that is only divisible by itself and 1 as well as negative itself and -1.
7 is prime since it is not divisible by any integer except for \(\pm 7\) and \(\pm 1\)
9 is not prime since 9 is divisible by 3 which is not \(\pm 9\) or \(\pm 1\).
We can "decompose" numbers into the prime numbers that were multiplied together to create them. This is called factoring.
Factor
- 24
- 30
- 90
Solution
- \(24 = 2 \cdot 2 \cdot 2 \cdot 3\)
- \(30 = 2 \cdot 3 \cdot 5\)
- \(90 = 2 \cdot 3\cdot 3 \cdot 5\)
A popular trick to use for factoring numbers is called a factor tree. Let's take a look at a simple example on how to do this. Let's decompose 6 into its prime factors
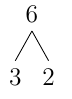
This involves dividing numbers until you get numbers that are prime. Here we note 6 is divisible by 3 and \(6\div 3=2\) so we broke 6 up into \(3\cdot 2\). We can't break this up anymore since 3 and 2 are prime.
Decompose 24 using a factor tree.
- Answer
-
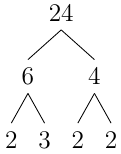
You can divide 24 by 4 to get 6. You can decompose 6 into 3 and 2. While you can decompose 4 into 2 and 2. So you can decompose 24 into \(2\cdot 3\cdot 2\cdot 2\) we see that 3 and 2 are prime so we can't decompose anymore. Notice that the factors produced are the same as in the previous example.
Decompose 30 using a factor tree.
- Answer
-
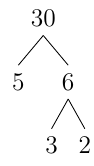
30 is divisible by 5 and \(30\div 5=6\) which we can decompose into 3 and 2.
So \(30=5\cdot 3\cdot 2\). This agrees with the answer in the previous example.
We see this isn't the only way to decompose 30 but you will still get the same result. For example you could have used 3 and 10 and decomposed 10 into 5 and 2 but the result is still \(30=5\cdot 3\cdot 2\)
Decompose 90 using a factor tree.
- Answer
-
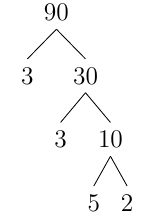
We can break 90 up into 3 and 30 and decompose 30.
So \(90=3\cdot 3\cdot 5\cdot 2\). This agrees with the example in the previous example.
Simplify Fractions
Try to input \(\frac{4}{8}\) and \(\frac{1}{2}\) into your calculator. What do you get? Why do you think the both inputs give you .5? It is because both of them express the same number. That is, 4 is half of 8 and 1 is half of 2. We can simplify \(\frac{4}{8}\) by decomposing 4 and 8 into a product of its primes, that is \(\frac{4}{8}=\frac{2\cdot2}{2\cdot 2\cdot 2}\). Now using the fact that we can break up a fraction, we can break up \(\frac{2\cdot2}{2\cdot 2\cdot 2}=\frac{2\cdot2\cdot 1}{2\cdot 2\cdot 2}=\frac{2}{2}\cdot \frac{2}{2}\cdot \frac{1}{2}=1\cdot1\cdot\frac{1}{2}=\frac{1}{2}\). This is why it is ok to cancel terms that are multiplied from the numerator and denominator. It is also common to just cross things out as in \(\frac{2\cdot2}{2\cdot 2\cdot 2}=\frac{\cancel{2}\cdot\cancel{2}}{\cancel{2}\cdot \cancel{2}\cdot 2}=\frac{1}{2}\).
There are many ways to write a fraction, some may say there is an infinite way to write the same fraction, but we usually write it in simplest form, that is when we can no longer cancel anything from the top and bottom.
Fractions that have the same value are equivalent fractions.
The Equivalent Fractions Property allows us to find equivalent fractions and also simplify fractions.
If \(a\), \(b\), and \(c\) are numbers where \(b\neq 0,c\neq 0\),
then \(\dfrac{a}{b}=\dfrac{a·c}{b·c}\) and \(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator.
For example,
\(\dfrac{2}{3}\) is simplified because there are no common factors of \(2\) and \(3\).
\(\dfrac{10}{15}\) is not simplified because \(5\) is a common factor of \(10\) and \(15\).
We simplify, or reduce, a fraction by removing the common factors of the numerator and denominator. A fraction is not simplified until all common factors have been removed. If an expression has fractions, it is not completely simplified until the fractions are simplified.
Sometimes it may not be easy to find common factors of the numerator and denominator. When this happens, it is a good idea to factor the numerator and the denominator into prime numbers using the factor tree, then cancel out the common factors using the Equivalent Fractions Property.
Simplify \(\dfrac{120}{252}\)
- Answer
-
Steps to solve the example. Step 1: Write out the factor trees 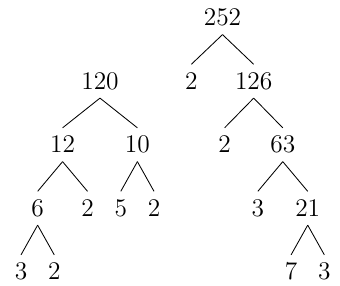
Step 2: Rewrite the fraction as a product (multiplication) of primes on the top and bottom. \(\dfrac{120}{252}=\dfrac{3\cdot2\cdot2\cdot5\cdot2}{2\cdot2\cdot3\cdot7\cdot3}\) Step 3: Cancel like terms from top and bottom \(=\dfrac{\cancel{3}\cdot\cancel{2}\cdot\cancel{2}\cdot 5\cdot2}{\cancel{2}\cdot\cancel{2}\cdot\cancel{3}\cdot7\cdot3}=\dfrac{5\cdot 2}{7\cdot 3}\) Step 4: Multiply to get 1 term on top and bottom, that is, in the numerator and denominator. \(\dfrac{5\cdot 2}{7\cdot 3}=\dfrac{10}{21}\)
Simplify \(\dfrac{−315}{770}\).
- Answer
-
Solution to the example. Step 1: Write out the factor trees 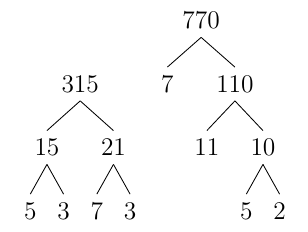
Step 2: Rewrite the fraction as a product (multiplication) of primes on the top and bottom. \(-\dfrac{315}{770}=-\dfrac{5\cdot 3\cdot 7\cdot 3}{7\cdot 11\cdot 5\cdot 2}\) Step 3: Cancel like terms from top and bottom \(=-\dfrac{\cancel{5}\cdot 3\cdot\cancel{7}\cdot 3}{\cancel{7}\cdot 11\cdot\cancel{5}\cdot 2}=-\dfrac{9}{22}\) Step 4: Multiply to get 1 term on top and bottom, that is, in the numerator and denominator. \(=-\dfrac{9}{22}\)
Simplify \(−\dfrac{69}{120}\).
- Answer
-
\(−\dfrac{23}{40}\)
Simplify \(−\dfrac{120}{192}\).
- Answer
-
\(−\dfrac{5}{8}\)
Multiplying Fractions
Multiplying fractions is a simple operation. All you do is multiple the numerator with the numerator and the denominator with the denominator. Let's first get an intuitive idea on why that works. First say you have \(\frac{1}{3}\) of a pizza and you multiplied it by 3, that is you put 3 \(\frac{1}{3}\) pizzas together. You would get 1 whole pizza! In math, this would look like \(3\cdot \frac{1}{3}=\frac{3}{1}\cdot\frac{1}{3}=\frac{3\cdot 1}{1\cdot3}=\frac{3}{3}=1\).
We can also go backwards as in we can rewrite \(\frac{2}{3}\) as \(2\cdot \frac{1}{3}\).
What about the denominators? Why do we multiply those? Say you have a whole pizza and you divide it into 3 equal slices. You then cut a slice in half to get two slices. We see that the small slices from the 2nd cut make up \(\frac{1}{6}\) of a pizza. This makes sense because if you cut each slice in half, you would have 6 equally sized slices and 1 slice from that would be \(\frac{1}{6}\) a pizza. So we divided a pizza by 3 and then each slice in 2. We can express this using an equation as \(\frac{1}{3}\cdot\frac{1}{2}=\frac{1}{3}\div 2=(1\div 3)\div 2=\frac{1}{6}\).
Now let's put all that intuition together.
Compute
\[\frac{2}{3}\cdot \frac{7}{5}\]
- Answer
-
\begin{align*}
\frac{2}{3}\cdot \frac{7}{5}&=\frac{2\cdot 7}{3\cdot 5}\\
&=\frac{14}{15}
\end{align*}
We that was way easier than all that intuition.
Let's do some more examples,
Compute the following:
- \(\frac{1}{4}\cdot \frac{1}{4}\)
- \(\frac{1}{3}\cdot -\frac{2}{3}\)
- \(-\frac{2}{3}\cdot -\frac{4}{5}\)
- Answer
-
- \(\frac{1\cdot 1}{4\cdot 4}=\frac{1}{16} \)
- \(-\frac{1\cdot 2}{3\cdot 3}=-\frac{2}{9} \)
- \(--\frac{2\cdot 4}{3\cdot 5}=\frac{8}{15} \)
Now lets combine these strategies to compute and simplify a product of fractions.
Compute \(\dfrac{2}{3}\cdot\dfrac{27}{4}\)
- Answer
-
Solution to previous example. Step 1: Rewrite every number as a product of primes. \(=\dfrac{2}{3}\cdot\dfrac{3\cdot 3\cdot 3}{2\cdot 2}\) Step 2: Multiply \(=\dfrac{2\cdot3\cdot3\cdot 3}{3\cdot2\cdot2}\) Step 3: Cancel like terms \(=\dfrac{3\cdot 3}{2}\) Step 4: Simplify if possible \(=\frac{9}{2}\)
Compound Fractions and Dividing Fractions
The numerators or denominators of some fractions contain fractions themselves. A fraction in which the numerator or the denominator is a fraction is called a compound fraction. Some people may use complex fraction but we will see later that this is actually terrible and horrible terminology. Still just know that complex fraction is the same as a compound fraction.
A compound fraction is a fraction in which the numerator or the denominator contains a fraction.
Some examples of compound fractions are:
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{ \frac{5}{6}}\]
To simplify a compound fraction, remember that the fraction bar means division. For example, the compound fraction \(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) means \(\dfrac{3}{4}÷\frac{5}{8}.\)
Surprisingly, division is just as easy as multiplication! All we need to do is take the top fraction and multiply it by the "reciprocal" of the bottom fraction.
The reciprocal of a number is the multiplicative inverse. That is, the number you need to multiply to it to get 1.
This is very easy for the rationals as we just need to switch the numerator with the denominator.
The reciprocal of \(2=\dfrac{1}{2}\) is \(\dfrac{1}{2}\) since \(2\cdot \dfrac{1}{2}=1\).
The reciprocal of \(\dfrac{3}{2}\) is \(\frac{2}{3}\) since \(\dfrac{3}{2}\cdot\dfrac{2}{3}=1\)
Now we can look at an intuitive example of dividing by a fraction. Lets say a child eats half a slice of pizza and you have a pizza that contains 8 slices. How many children can you feed with 8 slices? Well each child eats half a slice so you would be able to feed 2 children with each slice and you have 8 slices, so you can feed 16 children. In an equation, this looks like \[\dfrac{\dfrac{8}{1}}{\dfrac{1}{2}}=\dfrac{8}{1}\cdot\dfrac{2}{1}=\dfrac{16}{1}=16\]
Now lets get a bit more complicated with...teenagers...that eat \(\dfrac{3}{4}\) of a slice each. That is, each teenager eat 3 quarter slices. Say you have \(\dfrac{3}{2}\) slices of pizza, that is 3 half slices. How many teenagers can you feed with that? Well let's rewrite \(\dfrac{3}{2}\) as \(3 \cdot \dfrac{1}{2}\) and save the multiplication with \(\dfrac{1}{2}\) for later. Let's cut up 3 slices into quarter slices so we have \(3\cdot 4=12\) quarter slices. each teenager eats 3 quarter slices so we can feed \(\dfrac{12}{3}=4\) teenagers. BUT WAIT we had 3 half slices so we can actually feed \(4\cdot \dfrac{1}{2}=\dfrac{4}{2}=2\) teenagers. This is just
\[\dfrac{\dfrac{3}{2}}{\dfrac{3}{4}}=\dfrac{3}{2}\cdot\dfrac{4}{3}=\dfrac{12}{6}=2\]
WOW that was way easier than the intuition. You don't need to remember the intuitive examples for the test but hopefully you now understand why you are doing what you are doing. Now lets take a look at a step by step problem. To help with the examples, remember "invert and multiply"; this means that to divide, we flip over the denominator and multiply it by the numerator.
Compute \(\dfrac{\dfrac{9}{2}}{\dfrac{27}{4}}\)
- Answer
-
Solution to previous example. Step 1: Rewrite the quotient as a product. \(=\dfrac{9}{2}\cdot\dfrac{4}{27}\) Step 2: Rewrite every number as a product of primes. \(=\dfrac{3\cdot 3}{2}\cdot\dfrac{2\cdot 2}{3\cdot 3\cdot 3}\) Step 3: Multiply \(=\dfrac{3\cdot3\cdot2\cdot 2}{2\cdot3\cdot3\cdot 3}\) Step 4: Cancel like terms \(=\dfrac{2}{3}\) Step 5: Simplify if possible \(=\dfrac{2}{3}\)
This is the same process as above just with an extra step in the beginning.
Compute \(−\dfrac{7}{18}÷(−\dfrac{14}{27}).\)
- Answer
-
Solution to previous example. Step 1: Rewrite the quotient as a product. \(=-\dfrac{7}{18}\cdot-\dfrac{27}{14}\) Step 2: Rewrite every number as a product of primes. \(=-\dfrac{7}{3\cdot 3\cdot 2}\cdot-\dfrac{3\cdot 3\cdot 3}{7\cdot 2}\) Step 3: Multiply \(=\dfrac{7\cdot 3\cdot3\cdot 3}{3\cdot 3\cdot 2\cdot 7\cdot 2}\) Step 4: Cancel like terms \(=\dfrac{3}{2\cdot 2}\) Step 5: Simplify if possible \(=\dfrac{3}{4}\)
Divide: \(−\dfrac{7}{27}÷(−\dfrac{35}{36})\).
- Answer
-
\(\dfrac{4}{15}\)
Divide: \(−\dfrac{5}{14}÷(−\dfrac{15}{28}).\)
- Answer
-
\(\dfrac{2}{3}\)
Add and Subtract Fractions
Let's move on to addition. Say you have half a pizza and your friend has half a pizza, then between the two of you, you all have a whole pizza. That is, \(\frac{1}{2}+\frac{1}{2} = \frac{2}{2} = 1\). Note that we added the numerators together and left the denominators unchanged.
When we multiplied fractions, we just multiplied the numerators and multiplied the denominators right straight across. To add or subtract fractions, they must have a common denominator.
If \(a\), \(b\), and \(c\) are numbers where \(c≠0\), then
\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\]
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
What if the denominators are different? Then make them the same! We can make them the same by using a fundamental trick of math
A number multiplied by 1 is the same number. That is, if \(a\) is any number, then \(a\cdot 1=a\)
That doesn't seem like much of a trick but there are many creative ways to write the number 1.
For example \(\frac{2}{2}\) and \(\frac{62}{62}\) are 1.
The least common multiple (LCM) of two integers \(x,y\) is the smallest integer, \(c\) such that \(c\) is divisible by \(x\) and \(y\).
The LCM of 4 and 6 is 12 because 4 and 6 divide 12 and 12 is the smallest integer that both 6 and 4 divide evenly.
The LCM of 4 and 6 is not 24 because, even though 4 and 6 divide 24, it is not the smallest integer that both 6 and 4 divide evenly.
Let's do an example of how to find the LCM
Find the lcm of 8 and 12.
- Answer
-
Solution to previous example. Step 1: factor the numbers 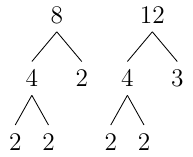
Step 2: multiply all the primes but skip repeats \(2\cdot 2 \cdot 2\cdot 3\) Step 3: Compute the lcm by doing the multiplication \(=24\) Note: Starting from left to right, we write down the three 2s we got from 8. We skip the two 2s from 12 since we already picked up three 2s from 8, and we pick up a 3 since we didn't already have it.
The least common denominator (LCD) of two fractions is the smallest number that can be used as a common denominator of the fractions. The LCD of the two fractions is the least common multiple (LCM) of their denominators.
The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
After we find the least common denominator of two fractions, we convert the fractions to equivalent fractions with the LCD. Putting these steps together allows us to add and subtract fractions because their denominators will be the same!
Let's first do an intuitive example.
Let's say you have half a pizza and a quarter of a pizza. How much pizza do you have all together and why is it \(\frac{3}{4}\)th of a pizza? We broke up the half of a pizza into 2 quarters of a pizza and then added them to the quarter of a pizza to get 3 quarters of a pizza. In an equation this looks like
\(\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{2}{4}+\dfrac{1}{4}=\dfrac{3}{4}\)
Did you notice that 4 is the LCM of 2 and 4? If we want to add fractions all we do is make them have the same denominator and the denominator that is easiest to work with is the LCM!
Compute \(\dfrac{3}{10}+\dfrac{2}{15}\)
- Answer
-
Solution to previous example. Step 1: Compute lcm of denominator if they are different, if same then skip to step 5. Solution to previous example. Substep 1: factor the denominators 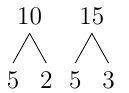
Substep 2: multiply all the primes but skip repeats \(5\cdot 2 \cdot 3\) Substep 3: Compute the lcm \(=30\) Step 2: divide the lcm by the denominators \(\dfrac{30}{10}=3, \dfrac{30}{15}=2\) Step 3: multiply the 1st numerator and denominator by the 1st number above.
\(\dfrac{3\cdot 3}{10\cdot 3}=\dfrac{9}{30}\)
This is where we multiply by a 1 since \(\dfrac{3}{10}=\dfrac{3}{10}\cdot 1=\dfrac{3}{10}\cdot\frac{3}{3}=\dfrac{3\cdot 3}{10\cdot 3}\). Same thing goes for the next step.
Step 4: multiply the 2nd numerator and denominator by the 2nd number above \(\dfrac{2\cdot 2}{15\cdot 2}=\dfrac{4}{30}\) Step 5: add the two numbers together \(\dfrac{9}{30}+\dfrac{4}{30}=\dfrac{13}{30}\) Step 6: Simplify if possible \(=\frac{13}{30}\)
This is the same procedure for subtraction too.
Compute \(\dfrac{2}{3}-\dfrac{4}{5}\)
- Answer
-
Solution to previous example. Step 1: Compute lcm of denominator Solution to previous example. Substep 1: factor the denominators 3 and 5 are both prime. Substep 2: multiply all the primes but skip repeats \(3 \cdot 5\) Substep 3: Compute the lcm =15 Step 2: divide the lcm by the denominators \(\frac{15}{3}=5\)
\(\frac{15}{5}=3\)
Step 3: multiply the 1st numerator and denominator by the 1st number above \(\frac{2\cdot 5}{3\cdot 5}=\frac{10}{15}\) Step 4: multiply the 2nd numerator and denominator by the 2nd number above \(\frac{4\cdot 3}{5\cdot 3}=\frac{12}{15}\) Step 5: subtract the two numbers \(\frac{10}{15}-\frac{12}{15}=-\frac{2}{15}\) Step 6: Simplify if possible \(=-\frac{2}{15}\)
Lets take a look at some more examples.
Add: \(\dfrac{7}{12}+\dfrac{11}{15}\).
- Answer
-
\(\dfrac{79}{60}\)
Add: \(\dfrac{13}{15}+\dfrac{17}{20}\).
- Answer
-
\(\dfrac{103}{60}\)
We now have all four operations for fractions. The Table below summarizes fraction operations.
| Fraction Multiplication | Fraction Division |
|---|---|
| \(\dfrac{a}{b}⋅\dfrac{c}{d}=\dfrac{ac}{bd}\) | \(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\) |
| Multiply the numerators and multiply the denominators | Multiply the first fraction by the reciprocal of the second. |
| Fraction Addition | Fraction Subtraction |
| \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) | \(\dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\) |
| Add the numerators and place the sum over the common denominator. | Subtract the numerators and place the difference over the common denominator. |
|
To multiply or divide fractions, an LCD is NOT needed. To add or subtract fractions, an LCD is needed. |
|
Use the Order of Operations to Simplify Fractions
The fraction bar in a fraction acts as grouping symbol. The order of operations then tells us to simplify the numerator and then the denominator. Then we divide.
- Simplify the expression in the numerator. Simplify the expression in the denominator.
- Simplify the fraction.
Simplify: \(\dfrac{4(−3)+6(−2)}{−3(2)−2}\).
- Answer
-
The fraction bar acts like a grouping symbol. So completely simplify the numerator and the denominator separately.
\(\begin{array}{lc} \text{} & \dfrac{4(−3)+6(−2)}{−3(2)−2} \\[5pt] \text{Multiply.} & \dfrac{−12+(−12)}{−6−2} \\[5pt] \text{Simplify.} & \dfrac{−24}{−8} \\[5pt] \text{Divide.} & 3 \end{array}\)
Simplify:\(\dfrac{8(−2)+4(−3)}{−5(2)+3}\).
- Answer
-
4
Simplify: \(\dfrac{7(−1)+9(−3)}{−5(3)−2}\).
- Answer
-
2
Now we’ll look at compound fractions where the numerator or denominator contains an expression that can be simplified. So we first must completely simplify the numerator and denominator separately using the order of operations. Then we divide the numerator by the denominator as the fraction bar means division.
Simplify \(\frac{\frac{1}{2}-\frac{5}{2}}{\frac{3}{5}+\frac{1}{5}}\)
- Answer
-
Solution to the example. Step 1: Simplify the numerator \(=\frac{-\frac{4}{2}}{\frac{3}{5}+\frac{1}{5}}\) Step 2: Simplify the denominator \(=\frac{-\frac{4}{2}}{\frac{4}{5}}\) Step 3: Compute the division \(=-\frac{4}{2}\cdot \frac{5}{4}=-\frac{5}{2}\) Step 4: Simplify if possible \(=-\frac{5}{2}\)\
Simplify: \(\dfrac{\left(\frac{1}{3}\right)}{2+2}\).
- Answer
-
\(\frac{1}{12}\)
Simplify: \(\dfrac{1+4\cdot 4}{\left(\frac{1}{4}\right)}\).
- Answer
-
68
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator.
- Simplify if possible.
Simplify: \(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}}\).
- Answer
-
It may help to put parentheses around the numerator and the denominator.
\(\begin{array}{lc}\text{} & \dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}} \\[6pt] \text{Simplify the numerator }(LCD=6)\text{ and } \\[6pt] \text{simplify the denominator }(LCD=12). & \dfrac{\left(\dfrac{3}{6}+\dfrac{4}{6}\right)}{\left(\dfrac{9}{12}−\dfrac{2}{12}\right)} \\[6pt] \text{Simplify.} & \left(\dfrac{7}{6}\right)\left(\dfrac{7}{12}\right) \\[6pt] \text{Divide the numerator by the denominator.} & \dfrac{7}{6}÷\dfrac{7}{12} \\[6pt] \text{Simplify.} & \dfrac{7}{6}⋅\dfrac{12}{7} \\[6pt] \text{Divide out common factors.} & \dfrac{\cancel{7}⋅\cancel{6}⋅2}{ \cancel{6}⋅\cancel{7}⋅1} \\[6pt] \text{Simplify.} & 2 \end{array}\)
Simplify: \( \dfrac{\dfrac{1}{3}+\dfrac{1}{2}}{ \dfrac{3}{4}−\dfrac{1}{3}}\).
- Answer
-
2
Simplify: \(\dfrac{\dfrac{2}{3}−\dfrac{1}{2}}{ \dfrac{1}{4}+\dfrac{1}{3}}\).
- Answer
-
\(\frac{2}{7}\)
Key Concepts
- If \(a\), \(b\), and \(c\) are numbers where \(b≠0,c≠0\), then
\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\) and \(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
- How to simplify a fraction.
- Rewrite the numerator and denominator to show the common factors.
If needed, factor the numerator and denominator into prime numbers first. - Simplify using the Equivalent Fractions Property by dividing out common factors.
- Multiply any remaining factors.
- Rewrite the numerator and denominator to show the common factors.
- If \(a\), \(b\), \(c\), and \(d\) are numbers where \(b≠0\), and \(d≠0\), then
\(\dfrac{a}{b}·\dfrac{c}{d}=\dfrac{ac}{bd}\)
To multiply fractions, multiply the numerators and multiply the denominators.
- If \(a\), \(b\), \(c\), and \(d\) are numbers where \(b≠0\),\(c≠0\), and \(d≠0\), then
\(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)
To divide fractions, we multiply the first fraction by the reciprocal of the second.
- If \(a\), \(b\), and \(c\) are numbers where \(c≠0\), then
\(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)
To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
- How to add or subtract fractions.
- Do they have a common denominator?
- Yes—go to step 2.
- No—rewrite each fraction with the LCD (least common denominator).
- Find the LCD.
- Change each fraction into an equivalent fraction with the LCD as its denominator.
- Add or subtract the fractions.
- Simplify, if possible.
- Do they have a common denominator?
- How to simplify an expression with a fraction bar.
- Simplify the expression in the numerator. Simplify the expression in the denominator.
- Simplify the fraction.
- For any positive numbers \(a\) and \(b\),
\(\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\)
- How to simplify compound fractions.
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator. Simplify if possible.
Glossary
- compound fraction
- A fraction in which the numerator or the denominator is a fraction is called a compound fraction.
- denominator
- In a fraction, written \(\dfrac{a}{b}\), where \(b≠0\), the denominator \(b\) is the number of equal parts the whole has been divided into.
- equivalent fractions
- Equivalent fractions are fractions that have the same value.
- fraction
- A fraction is written \(\dfrac{a}{b}\), where \(b≠0\), and a is the numerator and \(b\) is the denominator. A fraction represents parts of a whole.
- least common denominator
- The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
- numerator
- In a fraction, written \(\dfrac{a}{b}\), where \(b≠0\), the numerator a indicates how many parts are included.
- reciprocal
- The reciprocal of a fraction is found by inverting the fraction, placing the numerator in the denominator and the denominator in the numerator.

