1.7E: Exercises for Section 1.7

In exercises 1 - 6, evaluate each integral in terms of an inverse trigonometric function.

1) $\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}}$

Answer

$\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}} \quad = \quad \sin^{−1}x\bigg|^{\sqrt{3}/2}_0=\dfrac{π}{3}$

2) $\displaystyle ∫^{1/2}_{−1/2}\frac{dx}{\sqrt{1−x^2}}$

3) $\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}}$

Answer

$\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}} \quad = \quad \tan^{−1}x\bigg|^1_{\sqrt{3}}=−\dfrac{π}{12}$

4) $\displaystyle ∫^{\sqrt{3}}_{\frac{1}{\sqrt{3}}}\frac{dx}{1+x^2}$

5) $\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

Answer

$\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}} \quad = \quad \sec^{−1}x\bigg|^{\sqrt{2}}_1=\dfrac{π}{4}$

6) $\displaystyle ∫^{\frac{2}{\sqrt{3}}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

In exercises 7 - 12, find each indefinite integral, using appropriate substitutions.

7) $\displaystyle ∫\frac{dx}{\sqrt{9−x^2}}$

Answer

$\displaystyle ∫\frac{dx}{\sqrt{9−x^2}} \quad = \quad \sin^{−1}\left(\frac{x}{3}\right)+C$

8) $\displaystyle ∫\frac{dx}{\sqrt{1−16x^2}}$

9) $\displaystyle ∫\frac{dx}{9+x^2}$

Answer

$\displaystyle ∫\frac{dx}{9+x^2} \quad = \quad \frac{1}{3}\tan^{−1}\left(\frac{x}{3}\right)+C$

10) $\displaystyle ∫\frac{dx}{25+16x^2}$

11) $\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}}$

Answer

$\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}} \quad = \quad \frac{1}{3}\sec^{−1}\left(\frac{|x|}{3}\right)+C$

12) $\displaystyle ∫\frac{dx}{x\sqrt{4x^2−16}}$

13) Explain the relationship $\displaystyle −\cos^{−1}t+C=∫\frac{dt}{\sqrt{1−t^2}}=\sin^{−1}t+C.$ Is it true, in general, that $\cos^{−1}t=−\sin^{−1}t$?

Answer

$\cos(\frac{π}{2}−θ)=\sin θ.$ So, $\sin^{−1}t=\dfrac{π}{2}−\cos^{−1}t.$ They differ by a constant.

14) Explain the relationship $\displaystyle \sec^{−1}t+C=∫\frac{dt}{|t|\sqrt{t^2−1}}=−\csc^{−1}t+C.$ Is it true, in general, that $\sec^{−1}t=−\csc^{−1}t$?

15) Explain what is wrong with the following integral: $\displaystyle ∫^2_1\frac{dt}{\sqrt{1−t^2}}$.

Answer

$\sqrt{1−t^2}$ is not defined as a real number when $t>1$.

16) Explain what is wrong with the following integral: $\displaystyle ∫^1_{−1}\frac{dt}{|t|\sqrt{t^2−1}}$.

Answer

$\sqrt{t^2−1}$ is not defined as a real number when $-1 \lt t \lt 1$, and the integrand is undefined when $t = -1$ or $t = 1$.

In exercises 17 - 20, solve for the antiderivative of $f$ with $C=0$, then use a calculator to graph $f$ and the antiderivative over the given interval $[a,b]$. Identify a value of $C$ such that adding $C$ to the antiderivative recovers the definite integral $\displaystyle F(x)=∫^x_af(t)\,dt$.

17) [T] $\displaystyle ∫\frac{1}{\sqrt{9−x^2}}\,dx$ over $[−3,3]$

Answer

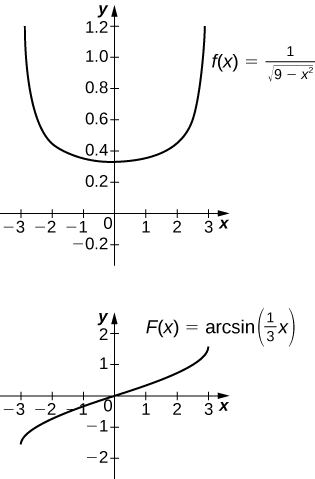
The antiderivative is $\sin^{−1}(\frac{x}{3})+C$. Taking $C=\frac{π}{2}$ recovers the definite integral.

18) [T] $\displaystyle ∫\frac{9}{9+x^2}\,dx$ over $[−6,6]$

19) [T] $\displaystyle ∫\frac{\cos x}{4+\sin^2x}\,dx$ over $[−6,6]$

Answer

The antiderivative is $\frac{1}{2}\tan^{−1}(\frac{\sin x}{2})+C$. Taking $C=\frac{1}{2}\tan^{−1}(\frac{\sin(6)}{2})$ recovers the definite integral.

20) [T] $\displaystyle ∫\frac{e^x}{1+e^{2x}}\,dx$ over $[−6,6]$

In exercises 21 - 26, compute the antiderivative using appropriate substitutions.

21) $\displaystyle ∫\frac{\sin^{−1}t}{\sqrt{1−t^2}}\,dt$

Answer

$\displaystyle ∫\frac{\sin^{−1}t\,dt}{\sqrt{1−t^2}} \quad = \quad \tfrac{1}{2}(\sin^{−1}t)^2+C$

22) $\displaystyle ∫\frac{dt}{\sin^{−1} t\sqrt{1−t^2}}$

23) $\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt$

Answer

$\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt \quad = \quad \frac{1}{4}(\tan^{−1}(2t))^2+C$

24) $\displaystyle ∫\frac{t\tan^{−1}(t^2)}{1+t^4}\,dt$

25) $\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt$

Answer

$\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt \quad = \quad \tfrac{1}{4}(\sec^{−1}\left(\tfrac{t}{2}\right))^2+C$

26) $\displaystyle ∫\frac{t\sec^{−1}(t^2)}{t^2\sqrt{t^4−1}}\,dt$

In exercises 27 - 32, use a calculator to graph the antiderivative of $f$ with $C=0$ over the given interval $[a,b]$. Approximate a value of $C$, if possible, such that adding $C$ to the antiderivative gives the same value as the definite integral $\displaystyle F(x)=∫^x_af(t)\,dt$.

27) [T] $\displaystyle ∫\frac{1}{x\sqrt{x^2−4}}\,dx$ over $[2,6]$

Answer

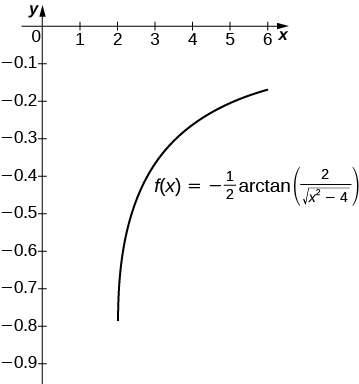
The antiderivative is $\frac{1}{2}\sec^{−1}(\frac{x}{2})+C$. Taking $C=0$ recovers the definite integral over $[2,6]$.

28) [T] $\displaystyle ∫\frac{1}{(2x+2)\sqrt{x}}\,dx$ over $[0,6]$

29) [T] $\displaystyle ∫\frac{(\sin x+x\cos x)}{1+x^2\sin^2x\,dx}$ over $[−6,6]$

Answer

The general antiderivative is $\tan^{−1}(x\sin x)+C$. Taking $C=−\tan^{−1}(6\sin(6))$ recovers the definite integral.

30) [T] $\displaystyle ∫\frac{2e^{−2x}}{\sqrt{1−e^{−4x}}}\,dx$ over $[0,2]$

31) [T] $\displaystyle ∫\frac{1}{x+x\ln 2x}$ over $[0,2]$

Answer

The general antiderivative is $\tan^{−1}(\ln x)+C$. Taking $\displaystyle C=\tfrac{π}{2}=\lim_{t \to ∞}\tan^{−1} t$ recovers the definite integral.

32) [T] $\displaystyle ∫\frac{\sin^{−1}x}{\sqrt{1−x^2}}$ over $[−1,1]$

In exercises 33 - 38, compute each integral using appropriate substitutions.

33) $\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt$

Answer

$\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt \quad = \quad \sin^{−1}(e^t)+C$

34) $\displaystyle ∫\frac{e^t}{1+e^{2t}}\,dt$

35) $\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}}$

Answer

$\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}} \quad = \quad \sin^{−1}(\ln t)+C$

36) $\displaystyle ∫\frac{dt}{t(1+\ln^2t)}$

37) $\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt$

Answer

$\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt \quad = \quad −\frac{1}{2}(\cos^{−1}(2t))^2+C$

38) $\displaystyle ∫\frac{e^t\cos^{−1}(e^t)}{\sqrt{1−e^{2t}}}\,dt$

In exercises 39 - 42, compute each definite integral.

39) $\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt$

Answer

$\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt \quad = \quad \frac{1}{2}\ln\left(\frac{4}{3}\right)$

40) $\displaystyle ∫^{1/2}_{1/4}\frac{\tan(\cos^{−1}t)}{\sqrt{1−t^2}}\,dt$

41) $\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt$

Answer

$\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt \quad = \quad 1−\frac{2}{\sqrt{5}}$

42) $\displaystyle ∫^{1/2}_0\frac{\cos(\tan^{−1}t)}{1+t^2}\,dt$

43) For $A>0$, compute $\displaystyle I(A)=∫^{A}_{−A}\frac{dt}{1+t^2}$ and evaluate $\displaystyle \lim_{a→∞}I(A)$, the area under the graph of $\dfrac{1}{1+t^2}$ on $[−∞,∞]$.

Answer

$2\tan^{−1}(A)→π$ as $A→∞$

44) For $1<B<∞$, compute $\displaystyle I(B)=∫^B_1\frac{dt}{t\sqrt{t^2−1}}$ and evaluate $\displaystyle \lim_{B→∞}I(B)$, the area under the graph of $\frac{1}{t\sqrt{t^2−1}}$ over $[1,∞)$.

45) Use the substitution $u=\sqrt{2}\cot x$ and the identity $1+\cot^2x=\csc^2x$ to evaluate $\displaystyle ∫\frac{dx}{1+\cos^2x}$. (Hint: Multiply the top and bottom of the integrand by $\csc^2x$.)

Answer

Using the hint, one has $\displaystyle ∫\frac{\csc^2x}{\csc^2x+\cot^2x}\,dx=∫\frac{\csc^2x}{1+2\cot^2x}\,dx.$ Set $u=\sqrt{2}\cot x.$ Then, $du=−\sqrt{2}\csc^2x$ and the integral is $\displaystyle −\tfrac{1}{\sqrt{2}}∫\frac{du}{1+u^2}=−\tfrac{\sqrt{2}}{2}\tan^{−1}u+C=\tfrac{\sqrt{2}}{2}\tan^{−1}(\sqrt{2}\cot x)+C$. If one uses the identity $\tan^{−1}s+\tan^{−1}(\frac{1}{s})=\frac{π}{2}$, then this can also be written $\tfrac{\sqrt{2}}{2}\tan^{−1}(\frac{\tan x}{\sqrt{2}})+C.$

46) [T] Approximate the points at which the graphs of $f(x)=2x^2−1$ and $g(x)=(1+4x^2)^{−3/2}$ intersect, and approximate the area between their graphs accurate to three decimal places.

47) [T] Approximate the points at which the graphs of $f(x)=x^2−1$ and $f(x)=x^2−1$ intersect, and approximate the area between their graphs accurate to three decimal places.

Answer

$x≈±1.13525.$ The left endpoint estimate with $N=100$ is 2.796 and these decimals persist for $N=500$.

48) Use the following graph to prove that $\displaystyle ∫^x_0\sqrt{1−t^2}\,dt=\frac{1}{2}x\sqrt{1−x^2}+\frac{1}{2}\sin^{−1}x.$