3.2E: Exercises for Section 3.2

In exercises 1 - 4, sketch the curves below by eliminating the parameter $t$. Give the orientation of the curve.

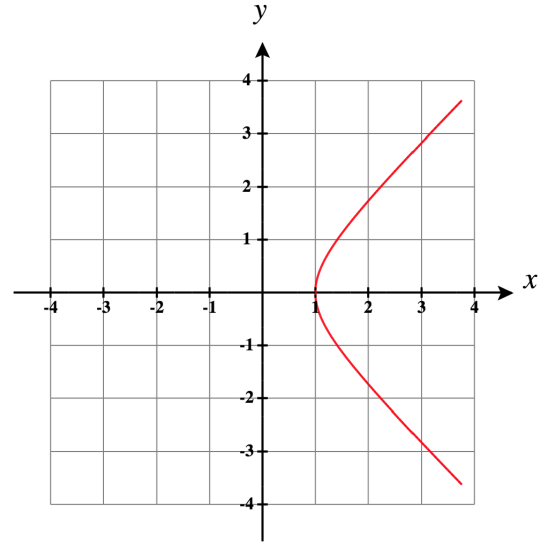
1) $x=t^2+2t, \quad y=t+1$

Answer

Orientation: bottom to top

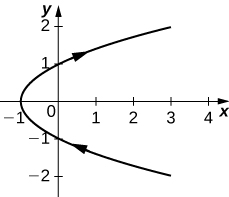
2) $x=\cos(t), \quad y=\sin(t), \quad \text{for } (0,2π]$

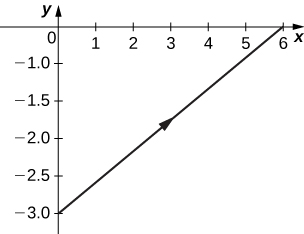
3) $x=2t+4, \quad y=t−1$

Answer

Orientation: left to right

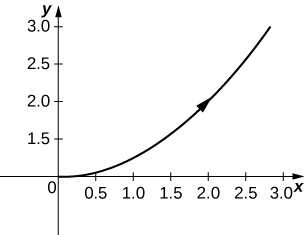
4) $x=3−t, \quad y=2t−3, \quad \text{for }1.5≤t≤3$

In exercise 5, eliminate the parameter and sketch the graph.

5) $x=2t^2,\quad y=t^4+1$

Answer

$y=\dfrac{x^2}{4}+1$

In exercises 6 - 9, use technology (CAS or calculator) to sketch the parametric equations.

6) [T] $x=t^2+t, \quad y=t^2−1$

7) [T] $x=e^{−t}, \quad y=e^{2t}−1$

Answer 

8) [T] $x=3\cos t, \quad y=4\sin t$

9) [T] $x=\sec t, \quad y=\cos t$

Answer

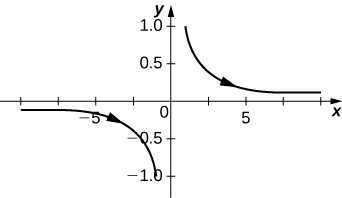
In exercises 10 - 20, sketch the parametric equations by eliminating the parameter. Indicate any asymptotes of the graph.

10) $x=e^t, \quad y=e^{2t}+1$

11) $x=6\sin(2θ), \quad y=-4\cos(2θ)$

Answer

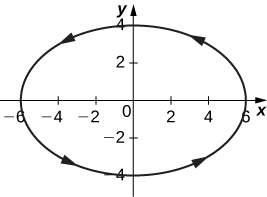
12) $x=\cos θ, \quad y=2\sin(2θ)$

13) $x=3−2\cos θ, \quad y=−5+3\sin θ$

Answer

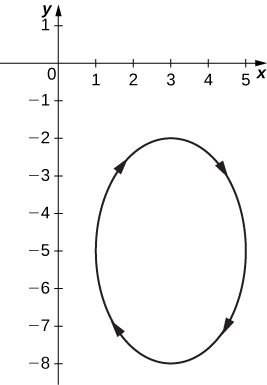
14) $x=4+2\cos θ, \quad y=−1+\sin θ$

15) $x=\sec t, \quad y=\tan t$

Answer

Asymptotes are $y=x$ and $y=−x$

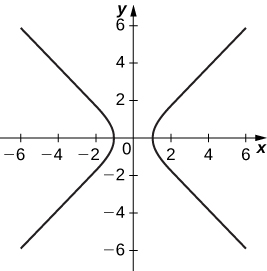
16) $x=\ln(2t), \quad y=t^2$

17) $x=e^t, \quad y=e^{2t}$

Answer

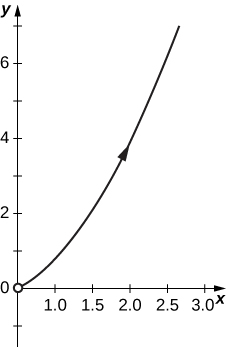
18) $x=e^{−2t}, \quad y=e^{3t}$

19) $x=t^3, \quad y=3\ln t$

Answer

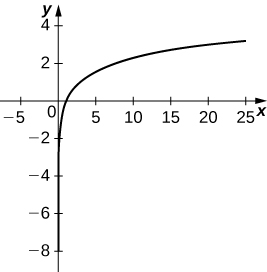
20) $x=4\sec θ, \quad y=3\tan θ$

In exercises 21 - 38, convert the parametric equations of a curve into rectangular form. No sketch is necessary. State the domain of the rectangular form.

21) $x=t^2−1, \quad y=\dfrac{t}{2}$

Answer

$x=4y^2−1;$ domain: $x∈[1,∞)$.

22) $x=\dfrac{1}{\sqrt{t+1}}, \quad y=\dfrac{t}{1+t}, \quad \text{for }t>−1$

23) $x=4\cos θ, \quad y=3\sin θ, \quad \text{for }t∈(0,2π]$

Answer

$\dfrac{x^2}{16}+\dfrac{y^2}{9}=1;$ domain $x∈[−4,4].$

24) $x=\cosh t, \quad y=\sinh t$

25) $x=2t−3, \quad y=6t−7$

Answer

$y=3x+2;$ domain: all real numbers.

26) $x=t^2, \quad y=t^3$

27) $x=1+\cos t, \quad y=3−\sin t$

Answer

$(x−1)^2+(y−3)^2=1$; domain: $x∈[0,2]$.

28) $x=\sqrt{t}, \quad y=2t+4$

29) $x=\sec t, \quad y=\tan t, \quad \text{for } π≤t<\frac{3π}{2}$

Answer

$y=\sqrt{x^2−1}$; domain: $x∈(−\infty,-1]$.

30) $x=2\cosh t, \quad y=4\sinh t$

31) $x=\cos(2t), \quad y=\sin t$

Answer

$y^2=\dfrac{1−x}{2};$ domain: $x∈[-1,1].$

32) $x=4t+3, \quad y=16t^2−9$

33) $x=t^2, \quad y=2\ln t, \quad \text{for }t≥1$

Answer

$y=\ln x;$ domain: $x∈[1,∞).$

34) $x=t^3, \quad y=3\ln t, \quad \text{for }t≥1$

35) $x=t^n, \quad y=n\ln t, \quad \text{for } t≥1,$ where $n$ is a natural number

Answer

$y=\ln x;$ domain: $x∈(0,∞).$

36) $x=\ln(5t), \quad y=\ln(t^2)$ where $1≤t≤e$

37) $x=2\sin(8t), \quad y=2\cos(8t)$

Answer

$x^2+y^2=4;$ domain: $x∈[−2,2].$

38) $x=\tan t, \quad y=\sec^2t−1$

In exercises 39 - 48, the pairs of parametric equations represent lines, parabolas, circles, ellipses, or hyperbolas. Name the type of basic curve that each pair of equations represents.

39) $x=3t+4, \quad y=5t−2$

Answer

line

40) $x−4=5t, \quad y+2=t$

41) $x=2t+1, \quad y=t^2−3$

Answer

parabola

42) $x=3\cos t, \quad y=3\sin t$

43) $x=2\cos(3t), \quad y=2\sin(3t)$

Answer

circle

44) $x=\cosh t, \quad y=\sinh t$

45) $x=3\cos t, \quad y=4\sin t$

Answer

ellipse

46) $x=2\cos(3t), \quad y=5\sin(3t)$

47) $x=3\cosh(4t) \quad y=4\sinh(4t)$

Answer

the right branch of a horizontally opening hyperbola

48) $x=2\cosh t, \quad y=2\sinh t$

49) Show that $x=h+r\cos θ, \quad y=k+r\sin θ$ represents the equation of a circle.

50) Use the equations in the preceding problem to find a set of parametric equations for a circle whose radius is $5$ and whose center is $(−2,3)$.

In exercises 51 - 53, use a graphing utility to graph the curve represented by the parametric equations and identify the curve from its equation.

51) [T] $x=θ+\sin θ, \quad y=1−\cos θ$

Answer

The equations represent a cycloid.

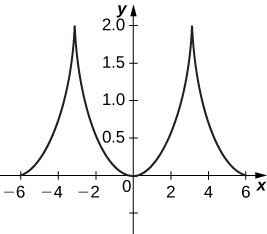
52) [T] $x=2t−2\sin t, \quad y=2−2\cos t$

53) [T] $x=t−0.5\sin t, \quad y=1−1.5\cos t$

Answer

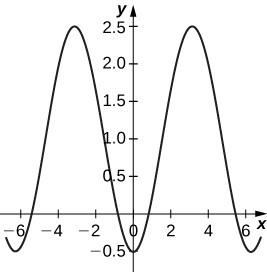
54) An airplane traveling horizontally at 100 m/s over flat ground at an elevation of 4000 meters must drop an emergency package on a target on the ground. The trajectory of the package is given by $x=100t, \quad y=−4.9t^2+4000, \quad \text{where }t≥0$ where the origin is the point on the ground directly beneath the plane at the moment of release. How many horizontal meters before the target should the package be released in order to hit the target?

55) The trajectory of a bullet is given by $x=v_0(\cos α)t, \quad y=v_0(\sin α)t−\frac{1}{2}gt^2$ where $v_0=500$ m/s, $g=9.8=9.8\text{ m/s}^2$, and $α=30$ degrees. When will the bullet hit the ground? How far from the gun will the bullet hit the ground?

Answer

22,092 meters at approximately 51 seconds.

56) [T] Use technology to sketch the curve represented by $x=\sin(4t), \quad y=\sin(3t), \quad \text{for }0≤t≤2π$.

57) [T] Use technology to sketch $x=2\tan(t), \quad y=3\sec(t), \quad \text{for }−π<t<π.$

Answer

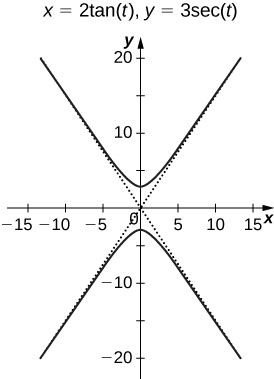
58) Sketch the curve known as an epitrochoid, which gives the path of a point on a circle of radius $b$ as it rolls on the outside of a circle of radius $a$. The equations are

$x=(a+b)\cos t−c⋅\cos\left[\frac{(a+b)t}{b}\right], \quad y=(a+b)\sin t−c⋅\sin\left[\frac{(a+b)t}{b}\right]$.

Let $a=1,\;b=2,\;c=1.$

59) [T] Use technology to sketch the spiral curve given by $x=t\cos(t), \quad y=t\sin(t)$ for $−2π≤t≤2π.$

Answer

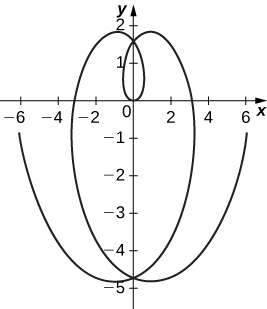
60) [T] Use technology to graph the curve given by the parametric equations $x=2\cot(t), \quad y=1−\cos(2t), \quad \text{for }−π/2≤t≤π/2.$ This curve is known as the witch of Agnesi.

61) [T] Sketch the curve given by parametric equations $x=\cosh(t), \quad y=\sinh(t),$ for $−2≤t≤2.$

Answer