5.E: Systems of ODEs (Exercises)

These are homework exercises to accompany Libl's "Differential Equations for Engineering" Textmap. This is a textbook targeted for a one semester first course on differential equations, aimed at engineering students. Prerequisite for the course is the basic calculus sequence.

3.1 Introduction to Systems of ODEs

Exercise $\PageIndex{3.1.1}$

Find the general solution of $x'_1 = x_2 - x_1 + t, x'_2 = x_2$.

Exercise $\PageIndex{3.1.2}$

Find the general solution of $x'_1 = 3x_1 - x_2 + e^t, x'_2 = x_1$.

Exercise $\PageIndex{3.1.3}$

Write $ay'' + by' + cy = f(x)$ as a first order system of ODEs.

Exercise $\PageIndex{3.1.4}$

Write $x'' + y^2y' - x^3 = \sin (t), y'' + {(x' + y')}^2 - x = 0$ as a first order system of ODEs.

Exercise $\PageIndex{3.1.5}$

Suppose two masses on carts on frictionless surface are at displacements $x_{1}$ and $x_{2}$ as in Example 3.1.3. Suppose that a rocket applies force $F$ in the positive direction on cart $x_{1}$. Set up the system of equations.

Example $\PageIndex{3.1.6}$

Suppose the tanks are as in Example 3.1.2, starting both at volume $V$, but now the rate of flow from tank 1 to tank 2 is $r_{1}$, and rate of flow from tank 2 to tank one is $r_{2}$. Notice that the volumes are now not constant. Set up the system of equations.

Exercise $\PageIndex{3.1.7}$

Find the general solution to $y'_1 = 3y_1, y'_2 = y_1 + y_2, y'_3 = y_1 + y_3$.

Answer

$y_{1}=C_{1}e^{3x}$, $y_{2}=y(x)=C_{2}e^{x}+\frac{C_{1}}{2}e^{3x}$, $y_{3}=y(x)=C_{3}e^{x}+\frac{C_{1}}{2}e^{3x}$

Exercise $\PageIndex{3.1.8}$

Solve $y' = 2x, x' = x + y, x(0) = 1, y(0) = 3$.

Answer

$x=\frac{5}{3}e^{2t}-\frac{2}{3}e^{-t}$, $y=\frac{5}{3}e^{2t}+\frac{4}{3}e^{-t}$

Exercise $\PageIndex{3.1.9}$

Write $x''' = x + t$ as a first order system.

Answer

$x_{1}'=x_{2}$, $x_{2}'=x_{3}$, $x_{3}'=x_{1}+t$

Exercise $\PageIndex{3.1.10}$

Write $y''_1 + y_1 + y_2 = t y''_2 + y_1 - y_2 = t^2$ as a first order system.

Answer

$y_{3}'+y_{1}+y_{2}=t$, $y_{4}'+y_{1}-y_{2}=t^{2}$, $y_{1}'=y_{3}$, $y_{2}'=y_{4}$

Exercise $\PageIndex{3.1.11}$

Suppose two masses on carts on frictionless surface are at displacements $x_{1}$ and $x_{2}$ as in Example 3.1.3. Suppose initial displacement is $x_{1}(0)=x_{2}(0)=0$, and initial velocity is $x_{1}'(0)=x_{2}'(0)=a$ for some number $a$. Use your intuition to solve the system, explain your reasoning.

Answer

$x_{1}=x_{2}=at$. Explanation of the intuition is left to reader.

Exercise $\PageIndex{3.1.12}$

Suppose the tanks are as in Example 3.1.2 except that clean water flows in at the rate $s$ liters per second into tank 1, and brine flows out of tank 2 and into the sewer also at the rate of $s$ liters per second.

1. Draw the picture.
2. Set up the system of equations.
3. Intuitively, what happens as $t$ goes to infinity, explain.

Answer

1. Left to reader
2. $x_{1}'=\frac{r}{V}(x_{2}-x_{1})$, $x_{2}'=\frac{r}{V}x_{1}-\frac{r-s}{V}x_{2}$.
3. As $t$ goes to infinity, both $x_{1}$ and $x_{2}$ go to zero, explanation is left to reader.

3.2: Matrices and linear systems

Exercise $\PageIndex{3.2.1}$

Solve $\begin {bmatrix} 1 & 2 \\ 3 & 4 \end {bmatrix} \vec {x} = \begin {bmatrix} 5 \\ 6 \end {bmatrix}$ by using matrix inverse.

Exercise $\PageIndex{3.2.2}$

Compute determinant of $\begin {bmatrix} 9 & -2 & -6 \\ -8 & 3 & 6 \\ 10 & -2 & -6 \end {bmatrix}$.

Exercise $\PageIndex{3.2.3}$

Compute determinant of $\begin {bmatrix} 1 & 2 & 3 & 1 \\ 4 & 0 & 5 & 0 \\ 6 & 0 & 7 & 0 \\ 8 & 0 & 10 & 1 \end {bmatrix}$. Hint: Expand along the proper row or column to make the calculations simpler.

Exercise $\PageIndex{3.2.4}$

Compute inverse of $\begin {bmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \\ 0 & 1 & 0 \end {bmatrix}$.

Exercise $\PageIndex{3.2.5}$

For which $h$ is $\begin {bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & h \end {bmatrix}$ not invertible? Is there only one such $h$? Are there several? Infinitely many?

Exercise $\PageIndex{3.2.6}$

For which $h$ is $\begin {bmatrix} h & 1 & 1 \\ 0 & h & 0 \\ 1 & 1 & h \end {bmatrix}$ not invertible? Find all such $h$.

Exercise $\PageIndex{3.2.7}$

Solve $\begin {bmatrix} 9 & -2 & -6 \\ -8 & 3 & 6 \\ 10 & -2 & -6 \end {bmatrix} \vec {x} = \begin {bmatrix} 1 \\ 2 \\ 3 \end {bmatrix}$.

Exercise $\PageIndex{3.2.8}$

Solve $\begin {bmatrix} 5 & 3 & 7 \\ 8 & 4 & 4 \\ 6 & 3 & 3 \end {bmatrix} \vec{x} = \begin {bmatrix} 2 \\ 0 \\ 0 \end {bmatrix}$.

Exercise $\PageIndex{3.2.9}$

Solve $\begin {bmatrix} 3 & 2 & 3 & 0 \\ 3 & 3 & 3 & 3 \\ 0 & 2 & 4 & 2 \\ 2 & 3 & 4 & 3 \end {bmatrix} \vec {x} = \begin {bmatrix} 2 \\ 0 \\ 4 \\ 1 \end {bmatrix}$.

Exercise $\PageIndex{3.2.10}$

Find 3 nonzero $2 \times 2$ matrices $A, B,$ and $C$ such that $AB = AC$ but $B \ne C$.

Exercise $\PageIndex{3.2.11}$

Compute determinant of $\begin {bmatrix} 1 & 1 & 1 \\ 2 & 3 & -5 \\ 1 & -1 & 0 \end {bmatrix}$

Answer

$-15$

Exercise $\PageIndex{3.2.12}$

Find $t$ such that $\begin {bmatrix} 1 & t \\ -1 & 2 \end {bmatrix}$ is not invertible.

Answer

$-2$

Exercise $\PageIndex{3.2.12}$

Solve $\begin {bmatrix} 1 & 1 \\ 1 & -1 \end {bmatrix} \vec{x} = \begin {bmatrix} 10 \\ 20 \end {bmatrix}$.

Answer

$\vec{x}=\left[\begin{array}{c}{15}\\{-5}\end{array}\right]$

Exercise $\PageIndex{3.2.12}$

Suppose $a, b, c$ are nonzero numbers. Let $M = \begin {bmatrix} a & 0 \\ 0 & b \end {bmatrix}, N = \begin {bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end {bmatrix}$.

1. Compute $M^{-1}$.
2. Compute $N^{-1}$.

Answer

1. $\left[\begin{array}{cc}{\frac{1}{a}}&{0}\\{0}&{\frac{1}{b}}\end{array}\right]$
2. $\left[\begin{array}{ccc}{\frac{1}{a}}&{0}&{0}\\{0}&{\frac{1}{b}}&{0}\\{0}&{0}&{\frac{1}{c}}\end{array}\right]$

3.3: Linear systems of ODEs

Exercise $\PageIndex{3.3.1}$

Write the system $x'_1 = 2x_1-3tx_2+\sin t$ and $x'_2=e^t\,x_1 - 3x_2 + \cos t$ in the form $\vec{x}'=P(t)\, \vec{x} + \vec{f}(t)$.

Exercise $\PageIndex{3.3.2}$

1. Verify that the system $\vec{x}' = \begin{bmatrix} 1&3 \\ 3&1 \end{bmatrix} \vec{x}$ has the two solutions $\begin{bmatrix} 1\\1 \end{bmatrix}e^{4t}$ and $\begin{bmatrix} 1\\-1\end{bmatrix} e^{-2t}$.
2. Write down the general solution.
3. Write down the general solution in the form $x_1 = ?$,$x_2 = ?$ (i.e. write down a formula for each element of the solution).

Exercise $\PageIndex{3.3.3}$

Verify that $\begin{bmatrix} 1\\1 \end{bmatrix}e^t$ and $\begin{bmatrix} 1\\-1 \end{bmatrix} e^t$ are linearly independent. Hint: Just plug in $t=0$.

Exercise $\PageIndex{3.3.4}$

Verify that $\begin{bmatrix} 1\\1\\0 \end{bmatrix}e^t$ and $\begin{bmatrix}1\\-1\\1 \end{bmatrix}e^t$ and $\begin{bmatrix} 1\\-1\\1 \end{bmatrix}e^{2t}$ are linearly independent. Hint: You must be a bit more tricky than in the previous exercise.

Exercise $\PageIndex{3.3.5}$

Verify that$\begin{bmatrix}t\\t^2 \end{bmatrix}$ and $\begin{bmatrix} t^3\\t^4 \end{bmatrix}$ are linearly independent.

Exercise $\PageIndex{3.3.6}$

Take the system $x_{1}'+x_{2}'=x_{1}$, $x_{1}'-x_{2}'=x_{2}$.

1. Write it in the form $A\vec{x}'=B\vec{x}$ for matrices $A$ and $B$.
2. Compute $A^{-1}$ and use that to write the system in the form $\vec{x}'=P\vec{x}$.

Exercise $\PageIndex{3.3.7}$

Are $\begin{bmatrix} e^{2t}\\e^t \end{bmatrix}$ and $\begin{bmatrix} e^t\\e^{2t} \end{bmatrix}$ linearly independent? Justify.

Answer

Yes.

Exercise $\PageIndex{3.3.8}$

Are $\begin{bmatrix} cosh(t) \\ 1 \end{bmatrix}$, $\begin{bmatrix} e^t \\1 \end{bmatrix}$ and $\begin{bmatrix} e^{-t} \\1 \end{bmatrix}$linearly independent? Justify.

Answer

No. $2\left[\begin{array}{c}{\cosh (t)}{1}\end{array}\right]-\left[\begin{array}{c}{e^{t}}\\{1}\end{array}\right]-\left[\begin{array}{c}{e^{-t}}\\{1}\end{array}\right]=\vec{0}$

Exercise $\PageIndex{3.3.9}$

Write $x' = 3x -y+e^t$ and $y'=tx$ in matrix notation.

Answer

$\left[\begin{array}{c}{x}\\{y}\end{array}\right]'=\left[\begin{array}{cc}{3}&{-1}\\{t}&{0}\end{array}\right]\left[\begin{array}{c}{x}\\{y}\end{array}\right]+\left[\begin{array}{c}{e^{t}}\\{0}\end{array}\right]$

Exercise $\PageIndex{3.3.10}$

1. Write $x'_1=2t\,x_2$ and $x'_2=2t\,x_2$ in matrix notation.
2. Solve and write the solution in matrix notation.Add exercises text here.

Answer

1. $\vec{x}'=\left[\begin{array}{cc}{0}&{2t}\\{0}&{2t}\end{array}\right]\vec{x}$
2. $\vec{x}=\left[\begin{array}{c}{C_{2}e^{t^{2}}+C_{1}} \\ {C_{2}e^{t^{2}}}\end{array}\right]$

3.4: Eigenvalue Method

Exercise $\PageIndex{3.4.1}$: (easy)

Let $A$ be a $3 \times 3$ matrix with an eigenvalue of $3$ and a corresponding eigenvector $\vec{v}= \left[ \begin{array}{c} 1 \\ -1 \\ 3 \end{array} \right]$. Find $A \vec{v}$.

Exercise $\PageIndex{3.4.2}$

1. Find the general solution of $x'_1=2x_1, x'_2=3x_2$ using the eigenvalue method (first write the system in the form $\vec{x}'=A\vec{x}$ ).
2. Solve the system by solving each equation separately and verify you get the same general solution.

Exercise $\PageIndex{3.4.3}$

Find the general solution of $x'_1 = 3x_1 +x_2, x'_2 =2x_1+4x_2$ using the eigenvalue method.

Exercise $\PageIndex{3.4.4}$

Find the general solution of $x'_1 =x_1-2x_2, x'_2=2x_1 x_2$ using the eigenvalue method. Do not use complex exponentials in your solution.

Exercise $\PageIndex{3.4.5}$

1. Compute eigenvalues and eigenvectors of $A= \left[ \begin{array}{ccc} 9 & -2 & -6 \\ -8 & 3 & 6 \\ 10 & -2 & -6 \end{array} \right]$.
2. Find the general solution of $\vec{x}'=A\vec{x}$.

Exercise $\PageIndex{3.4.6}$

Compute eigenvalues and eigenvectors of $\left[ \begin{array}{ccc} -2 & -1 & -1 \\ 3 & 2 & 1 \\ -3 & -1 & 0 \end{array} \right].$

Exercise $\PageIndex{3.4.7}$

Let $a, b, c, d, e, f$ be numbers. Find the eigenvalues of $\left[ \begin{array}{ccc} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{array} \right].$

Exercise $\PageIndex{3.4.8}$

1. Compute eigenvalues and eigenvectors of $A= \left[ \begin{array}{ccc} 1 & 0 & 3 \\ -1 & 0 & 1 \\ 2 & 0 & 2 \end{array} \right]$.
2. Solve the system $\vec{x}'=A\vec{x}$.

Answer

1. Eigenvalues: $4,\:0,\:-1$ Eigenvectors: $\left[\begin{array}{c}{1}\\{0}\\{1}\end{array}\right]$, $\left[\begin{array}{c}{0}\\{1}\\{0}\end{array}\right]$, $\left[\begin{array}{c}{3}\\{5}\\{-2}\end{array}\right]$
2. $\vec{x}=C_{1}\left[\begin{array}{c}{1}\\{0}\\{1}\end{array}\right] e^{4t}+C_{2}\left[\begin{array}{c}{0}\\{1}\\{0}\end{array}\right]+C_{3}\left[\begin{array}{c}{3}\\{5}\\{-2}\end{array}\right]$

Exercise $\PageIndex{3.4.9}$

1. Compute eigenvalues and eigenvectors of $A= \left[ \begin{array}{cc} 1 & 1 \\ -1 & 0 \end{array} \right].$
2. Solve the system $\vec{x}'=A\vec{x}$.

Answer

1. Eigenvalues: $\frac{1+\sqrt{3}i}{2}$, $\frac{1-\sqrt{3}i}{2}$, Eigenvectors: $\left[\begin{array}{c}{-2}\\{1-\sqrt{3}i}\end{array}\right]$, $\left[\begin{array}{c}{-2}\\{1+\sqrt{3}i}\end{array}\right]$
2. $\vec{x}=C_{1}e^{t/2}\left[\begin{array}{c}{-2\cos\left(\frac{\sqrt{3}t}{2}\right)}\\{\cos\left(\frac{\sqrt{3}t}{2}\right)+\sqrt{3}\sin\left(\frac{\sqrt{3}t}{2}\right)}\end{array}\right]+C_{2}e^{t/2}\left[\begin{array}{c}{-2\sin\left(\frac{\sqrt{3}t}{2}\right)}\\{\sin\left(\frac{\sqrt{3}t}{2}\right)-\sqrt{3}\cos\left(\frac{\sqrt{3}t}{2}\right)}\end{array}\right]$

Exercise $\PageIndex{3.4.10}$

Solve $x'_1=x_2, x'_2=x_1$ using the eigenvalue method.

Answer

$\vec{x}=C_{1}\left[\begin{array}{c}{1}\\{1}\end{array}\right]e^{t}+C_{2}\left[\begin{array}{c}{1}\\{-1}\end{array}\right]e^{-t}$

Exercise $\PageIndex{3.4.11}$

Solve $x'_1=x_2, x'_2=-x_1$ using the eigenvalue method.

Answer

$\vec{x}=C_{1}\left[\begin{array}{c}{\cos(t)}\\{-\sin(t)}\end{array}\right]+C_{2}\left[\begin{array}{c}{\sin(t)}\\{\cos(t)}\end{array}\right]$

3.5: Two dimensional systems and their vector fields

Exercise $\PageIndex{3.5.1}$

Take the equation $m{x}'' + c{x}'+kx =0$, with $m>0, c\geq 0, k>0$ for the mass-spring system.

1. Convert this to a system of first order equations.
2. Classify for what $m$, $c$, $k$ do you get which behavior.
3. Can you explain from physical intuition why you do not get all the different kinds of behavior here?

Exercise $\PageIndex{3.5.2}$

Can you find what happens in the case when $P =\begin{bmatrix} 1&1\\ 0&1 \end{bmatrix}$? In this case the eigenvalue is repeated and there is only one eigenvector. What picture does this look like?

Exercise $\PageIndex{3.5.3}$

Can you find what happens in the case when $P = \begin{bmatrix} 1&1\\1&1 \end{bmatrix}$? Does this look like any of the pictures we have drawn?

Exercise $\PageIndex{3.5.4}$

Which behaviors are possible if $P$ is diagonal, that is $P=\left[\begin{array}{cc}{a}&{0}\\{0}&{b}\end{array}\right]$? You can assume that $a$ and $b$ are not zero.

Exercise $\PageIndex{3.5.5}$

Take the system from Example 3.1.2, $x_{1}'=\frac{r}{V}(x_{2}-x_{1})$, $x_{2}'=\frac{r}{V}(x_{1}-x_{2})$. As we said, one of the eigenvalues is zero. What is the other eigenvalue, how does the picture look like and what happens when $t$ goes to infinity.

Exercise $\PageIndex{3.5.6}$

Describe the behavior of the following systems without solving:

1. $x' = x + y,\quad y' = x- y$
2. $x_1' = x_1 + x_2,\quad x_2' = 2x_2$
3. $x_1' = -2x_2,\quad x_2' = 2x_1$
4. $x' = x+ 3y,\quad y' = -2x-4y$
5. $x' = x - 4y,\quad y' = -4x+y$

Answer

1. Two eigenvalues: $\pm\sqrt{2}$ so the behavior is a saddle.
2. Two eigenvalues: $1$ and $2$, so the behavior is a source.
3. Two eigenvalues: $\pm 2i$, so the behavior is a center (ellipses).
4. Two eigenvalues: $−1$ and $−2$, so the behavior is a sink.
5. Two eigenvalues: $5$ and $−3$, so the behavior is a saddle.

Exercise $\PageIndex{3.5.7}$

Suppose that $\vec{x} = A \vec{x}$ where $A$ is a $2 \times 2$ matrix with eigenvalues $2\pm i$. Describe the behavior.

Answer

Spiral source.

Exercise $\PageIndex{3.5.8}$

Take $\begin{bmatrix} x\\y \end{bmatrix}' = \begin{bmatrix} 0&1 \\0&0 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}$. Draw the vector field and describe the behavior. Is it one of the behaviours that we have seen before?

Answer

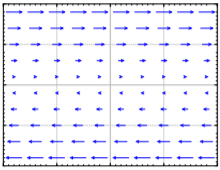
The solution does not move anywhere if $y=0$. When $y$ is positive, the solution moves (with constant speed) in the positive $x$ direction. When $y$ is negative, the solution moves (with constant speed) in the negative $x$ direction. It is not one of the behaviors we saw. Note that the matrix has a double eigenvalue $0$ and the general solution is $x=C_{1}t+C_{2}$ and $y=C_{1}$, which agrees with the description

3.6: Second order systems and applications

Exercise $\PageIndex{3.6.1}$

Find a particular solution to

$$\vec{x}'' = \left[ \begin{array}{cc} -3 & 1 \\ 2 & -2 \end{array} \right] \vec{x} + \left[ \begin{array}{c} 0 \\ 2 \end{array} \right] \cos(2t).$$

Exercise $\PageIndex{3.6.2}$: challenging

Let us take the example in Figure 3.6.3 with the same parameters as before: $m_1=2, k_1=4,$ and $k_2=2,$ except for $m_2$, which is unknown. Suppose that there is a force $\cos(5t)$ acting on the first mass. Find an $m_2$ such that there exists a particular solution where the first mass does not move.

Note

This idea is called dynamic damping. In practice there will be a small amount of damping and so any transient solution will disappear and after long enough time, the first mass will always come to a stop.

Example $\PageIndex{3.6.3}$

Let us take the Example 3.6.2, but that at time of impact, cart 2 is moving to the left at the speed of $3\:\frac{\text{m}}{\text{s}}$.

1. Find the behavior of the system after linkup.
2. Will the second car hit the wall, or will it be moving away from the wall as time goes on?
3. At what speed would the first car have to be traveling for the system to essentially stay in place after linkup?

Exercise $\PageIndex{3.6.4}$

Let us take the example in Figure 3.6.2 with parameters $m_1=m_2=1, k_1=k_2=1$. Does there exist a set of initial conditions for which the first cart moves but the second cart does not? If so, find those conditions. If not, argue why not.

Exercise $\PageIndex{3.6.5}$

Find the general solution to

$$\left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{array} \right] \vec{x}''=\left[ \begin{array}{ccc} -3 & 0 & 0 \\ 2 & -4 & 0 \\ 0 & 6 & -3 \end{array} \right] \vec{x}+\left[ \begin{array}{c} \cos(2t) \\ 0 \\ 0 \end{array} \right].$$

Answer

$\vec{x}=\left[\begin{array}{c}{1}\\{-1}\\{1}\end{array}\right]\left( a_{1}\cos (\sqrt{3} t)+b_{1}\sin (\sqrt{3} t)\right) +\left[\begin{array}{c}{0}\\{1}\\{-2}\end{array}\right]\left( a_{2}\cos (\sqrt{2} t)+b_{2}\sin (\sqrt{2} t)\right) +\left[\begin{array}{c}{0}\\{0}\\{1}\end{array}\right]\left( a_{3}\cos (t)+b_{3}\sin (t)\right) +\left[\begin{array}{c}{-1}\\{1/2}\\{2/3}\end{array}\right]\cos (2t)$

Exercise $\PageIndex{3.6.6}$

Suppose there are three carts of equal mass $m$ and connected by two springs of constant $k$ (and no connections to walls). Set up the system and find its general solution.

Answer

$\left[\begin{array}{ccc}{m}&{0}&{0}\\{0}&{m}&{0}\\{0}&{0}&{m}\end{array}\right]\vec{x}''=\left[\begin{array}{c}{-k}&{k}&{0}\\{k}&{-2k}&{k}\\{0}&{k}&{-k}\end{array}\right]\vec{x}$.

Solution: $\vec{x}=\left[\begin{array}{c}{1}\\{-2}\\{1}\end{array}\right]\left( a_{1}\cos (\sqrt{3k/m} t)+b_{1}\sin (\sqrt{3k/m} t)\right) + \left[\begin{array}{c}{1}\\{0}\\{-1}\end{array}\right]\left( a_{2}\cos (\sqrt{k/m} t)+b_{2}\sin (\sqrt{k/m} t)\right) +\left[\begin{array}{c}{1}\\{1}\\{1}\end{array}\right](a_{3}t+b_{3})$.

Exercise $\PageIndex{3.6.7}$

Suppose a cart of mass $2\text{ kg}$ is attached by a spring of constant $k=1$ to a cart of mass $3\text{ kg}$, which is attached to the wall by a spring also of constant $k=1$. Suppose that the initial position of the first cart is $1$ meter in the positive direction from the rest position, and the second mass starts at the rest position. The masses are not moving and are let go. Find the position of the second mass as a function of time.

Answer

$x_{2}=\left(\frac{2}{5}\right)\cos\left(\sqrt{\frac{1}{6}}t\right)-\left(\frac{2}{5}\right)\cos (t)$

3.7: Multiple Eigenvalues

Exercise $\PageIndex{3.7.1}$

Let $A = \begin{bmatrix} 5&-3 \\3&-1 \end{bmatrix}$. Find the general solution of $\vec{x}' = A\vec{x}$.

Exercise $\PageIndex{3.7.2}$

Let $A =\begin{bmatrix} 5&-4&4\\ 0&3&0 \\-2&4&-1\end{bmatrix}.$

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}' = A\vec{x}$.

Exercise $\PageIndex{3.7.3}$

Let $A = \begin{bmatrix} 2&1&0\\0&2&0\\0&0&2\end{bmatrix}$.

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}' = A\vec{x}$ in two different ways and verify you get the same answer.

Exercise $\PageIndex{3.7.4}$

Let $A = \begin{bmatrix}0&1&2 \\ -1&-2&-2\\-4&4&7 \end{bmatrix}$.

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}' = A\vec{x}$.

Exercise $\PageIndex{3.7.5}$

Let $A = \begin{bmatrix} 0&4&-2\\-1&-4&1\\0&0&-2 \end{bmatrix}$.

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}' = A \vec{x}$.

Exercise $\PageIndex{3.7.6}$

Let $\begin{bmatrix} 2&1&-1\\ -1&0&2\\-1&-2&4 \end{bmatrix}$.

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}' = A \vec{x}$.

Exercise $\PageIndex{3.7.7}$

Suppose that A is a $2 \times 2$ matrix with a repeated eigenvalue $\lambda$. Suppose that there are two linearly independent eigenvectors. Show that $A = \lambda I$.

Exercise $\PageIndex{3.7.8}$

Let $A = \begin{bmatrix} 1&1&1\\1&1&1\\1&1&1 \end{bmatrix}$.

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}' = A \vec{x}$.

Answer

1. $3,\:0,\:0$
2. No defects.
3. $\vec{x}=C_{1}\left[\begin{array}{c}{1}\\{1}\\{1}\end{array}\right]e^{3t}+C_{2}\left[\begin{array}{c}{1}\\{0}\\{-1}\end{array}\right]+C_{3}\left[\begin{array}{c}{0}\\{1}\\{-1}\end{array}\right]$

Exercise $\PageIndex{3.7.9}$

Let $A = \begin{bmatrix} 1&3&3 \\ 1&1&0 \\-1&1&2\end{bmatrix}$.

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}' = A \vec{x}$.

Answer

1. $1,\:1,\:2$
2. Eigenvalue $1$ has a defect of $1$
3. $\vec{x}=C_{1}\left[\begin{array}{c}{0}\\{1}\\{-1}\end{array}\right]e^{t}+C_{2}\left(\left[\begin{array}{c}{1}\\{0}\\{0}\end{array}\right]+t\left[\begin{array}{c}{0}\\{1}\\{-1}\end{array}\right]\right)e^{t}+C_{3}\left[\begin{array}{c}{3}\\{3}\\{-2}\end{array}\right]e^{2t}$

Exercise $\PageIndex{3.7.10}$

Let $A = \begin{bmatrix} 2&0&0 \\-1&-1&9\\0&-1&5\end{bmatrix}$.

1. What are the eigenvalues?
2. What is/are the defect(s) of the eigenvalue(s)?
3. Find the general solution of $\vec{x}'= A \vec{x}$.

Answer

1. $2,\:2,\:2$
2. Eigenvalue $2$ has a defect of $2$
3. $\vec{x}=C_{1}\left[\begin{array}{c}{0}\\{3}\\{1}\end{array}\right]e^{2t}+C_{2}\left(\left[\begin{array}{c}{0}\\{-1}\\{0}\end{array}\right]+t\left[\begin{array}{c}{0}\\{3}\\{1}\end{array}\right]\right)e^{2t}+C_{3}\left(\left[\begin{array}{c}{1}\\{0}\\{0}\end{array}\right]+t\left[\begin{array}{c}{0}\\{-1}\\{0}\end{array}\right]+\frac{t^{2}}{2}\left[\begin{array}{c}{0}\\{3}\\{1}\end{array}\right]\right)e^{2t}$

Exercise $\PageIndex{3.7.11}$

Let $A = \begin{bmatrix} a&a\\b&c\end{bmatrix}$, where $a$, $b$, and $c$ are unknowns. Suppose that 5 is a doubled eigenvalue of defect 1, and suppose that $\begin{bmatrix} 1\\0 \end{bmatrix}$ is the eigenvector. Find $A$ and show that there is only one solution.

Answer

$A=\left[\begin{array}{cc}{5}&{5}\\{0}&{5}\end{array}\right]$

3.8: Matrix Exponentials

Exercise $\PageIndex{3.8.1}$

Using the matrix exponential, find a fundamental matrix solution for the system , $x' = 3x +y, y' = x+ 3y$.

Exercise $\PageIndex{3.8.2}$

Find $e^{tA}$ for the matrix $A = \begin{bmatrix} 2&3\\0&2 \end{bmatrix}$.

Exercise $\PageIndex{3.8.3}$

Find a fundamental matrix solution for the system , $x'_1 =7x_1 +4x_2 +12x_3,~~~ x'_2= x_1 + 2x_2 +x_3,~~~x'_3 = -3x_1 - 2x_2 -5x_3$. Then find the solution that satisfies $\vec{x} = \begin{bmatrix}0\\1\\-2\end{bmatrix}$.

Exercise $\PageIndex{3.8.4}$

Compute the matrix exponential $e^A$ for $A = \begin{bmatrix} 1&2\\0&2\end{bmatrix}$.

Exercise $\PageIndex{3.8.5}$: (challenging)

Suppose $AB=BA$ . Show that under this assumption, $e^{A+B} = e^A e^B$.

Exercise $\PageIndex{3.8.6}$

Use Exercise $\PageIndex{3.8.5}$ to show that $(e^A)^{-1} = e^{-A}$. In particular this means that $e^A$ is invertible even if A is not.

Exercise $\PageIndex{3.8.7}$

Suppose $A$ is a matrix with eigenvalues $-1$, $1$, and corresponding eigenvectors $\begin{bmatrix} 1\\1\end{bmatrix}$, $\begin{bmatrix}0\\1\end{bmatrix}$.

1. Find matrix $A$ with these properties.
2. Find the fundamental matrix solution to $\vec{x}' = A \vec{x}$.
3. Solve the system in with initial conditions $\vec{x}(0) = \begin{bmatrix} 2\\3 \end{bmatrix}$.

Exercise $\PageIndex{3.8.8}$

Suppose that $A$ is an $n \times n$ matrix with a repeated eigenvalue $\lambda$ of multiplicity n. Suppose that there are n linearly independent eigenvectors. Show that the matrix is diagonal, in particular $A = \lambda \mathit{I}$. Hint: Use diagonalization and the fact that the identity matrix commutes with every other matrix.

Exercise $\PageIndex{3.8.9}$

Let $A =\begin{bmatrix} -1&-1\\1&-3 \end{bmatrix}$.

1. Find $e^{tA}$.
2. Solve $\vec{x}' = A \vec{x}$, $\vec{x}(0) = \begin{bmatrix} 1\\-2 \end{bmatrix}$.

Exercise $\PageIndex{3.8.10}$

Let $A = \begin{bmatrix} 1&2\\3&4 \end{bmatrix}$. Approximate $e^{tA}$ by expanding the power series up to the third order.

Exercise $\PageIndex{3.8.11}$

For any positive integer $n$, find a formula (or a recipe) for $A^{n}$ for the following matrices:

1. $\left[\begin{array}{cc}{3}&{0}\\{0}&{9}\end{array}\right]$
2. $\left[\begin{array}{cc}{5}&{2}\\{4}&{7}\end{array}\right]$
3. $\left[\begin{array}{cc}{0}&{1}\\{0}&{0}\end{array}\right]$
4. $\left[\begin{array}{cc}{2}&{1}\\{0}&{2}\end{array}\right]$

Exercise $\PageIndex{3.8.12}$

Compute $e^{tA}$ where $A = \begin{bmatrix} 1&-2\\-2&1\end{bmatrix}$.

Answer

$e^{tA}=\left[\begin{array}{cc}{\frac{e^{3t}+e^{-t}}{2}}&{\frac{e^{-t}-e^{3t}}{2}}\\{\frac{e^{-t}-e^{3t}}{2}}&{\frac{e^{3t}+e^{-t}}{2}}\end{array}\right]$

Exercise $\PageIndex{3.8.13}$

Compute $e^{tA}$ where $A=\begin{bmatrix} 1&-3&2\\-2&1&2\\-1&-3&4 \end{bmatrix}$.

Answer

$e^{tA}=\left[\begin{array}{ccc}{2e^{3t}-4e^{2t}+3e^{t}}&{\frac{3e^{t}}{2}-\frac{3e^{3t}}{2}}&{-e^{3t}+4e^{2t}-3e^{t}}\\{2e^{t}-2e^{2t}}&{e^{t}}&{2e^{2t}-2e^{t}}\\{2e^{3t}-5e^{2t}+3e^{t}}&{\frac{3e^{t}}{2}-\frac{3e^{3t}}{2}}&{-e^{3t}+5e^{2t}-3e^{t}}\end{array}\right]$

Exercise $\PageIndex{3.8.14}$

1. Compute $e^{tA}$ where $A = \begin{bmatrix} 3& -1\\1&1\end{bmatrix}$.
2. Solve $\vec{x} ' = A \vec{x}$ for $\vec{x}(0) = \begin{bmatrix} 1\\2 \end{bmatrix}$.

Answer

1. $e^{tA}=\left[\begin{array}{cc}{(t+1)e^{2t}}&{-te^{2t}}\\{te^{2t}}&{(1-t)e^{2t}}\end{array}\right]$
2. $\vec{x}=\left[\begin{array}{c}{(1-t)e^{2t}}\\{(2-t)e^{2t}}\end{array}\right]$

Exercise $\PageIndex{3.8.15}$

Compute the first 3 terms (up to the second degree) of the Taylor expansion of $e^{tA}$ where $A =\begin{bmatrix} 2&3\\2&2 \end{bmatrix}$ (Write as a single matrix). Then use it to approximate $e^{0.1A}$.

Answer

$\left[\begin{array}{cc}{1+2t+5t^{2}}&{3t+6t^{2}}\\{2t+4t^{2}}&{1+2t+5t^{2}}\end{array}\right]$ $e^{0.1A}\approx\left[\begin{array}{cc}{1.25}&{0.36}\\{0.24}&{1.25}\end{array}\right]$

Exercise $\PageIndex{3.8.16}$

For any positive integer $n$, find a formula (or a recipe) for $A^{n}$ for the following matrices:

1. $\left[\begin{array}{cc}{7}&{4}\\{-5}&{-2}\end{array}\right]$
2. $\left[\begin{array}{cc}{-3}&{4}\\{-6}&{-7}\end{array}\right]$
3. $\left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right]$

Answer

1. $\left[\begin{array}{cc}{5(3^{n})-2^{n+2}}&{4(3^{n})-2^{n+2}}\\{5(2^{n})-5(3^{n})}&{5(2^{n})-4(3^{n})}\end{array}\right]$
2. $\left[\begin{array}{cc}{3-2(3^{n})}&{2(3^{n})-2}\\{3-3^{n+1}}&{3^{n+1}-2}\end{array}\right]$
3. $\left[\begin{array}{cc}{1}&{0}\\{0}&{1}\end{array}\right]$ if $n$ is even, and $\left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right]$ if $n$ is odd.

3.9: Nonhomogeneous Systems

Exercise $\PageIndex{3.9.1}$

Find a particular solution to $x'=x+2y+2t,\: y'=3x+2y-4$,

1. using integrating factor method,
2. using eigenvector decomposition,
3. using undetermined coefficients.

Exercise $\PageIndex{3.9.2}$

Find the general solution to $x'=4x+y-1,\: y'=x+4y-e^t$,

1. using integrating factor method,
2. using eigenvector decomposition,
3. using undetermined coefficients.

Exercise $\PageIndex{3.9.3}$

Find the general solution to $x_1''=-6x_1+3x_2+ \cos(t),\: x''_2=2x_1-7x_2+ 3 \cos(t)$,

1. using eigenvector decomposition,
2. using undetermined coefficients.

Exercise $\PageIndex{3.9.4}$

Find the general solution to $x''_1=-6x_1+3x_2 + \cos(2t),\: x''_2=2x_1-7x_2+ \cos(2t)$,

1. using eigenvector decomposition,
2. using undetermined coefficients.

Exercise $\PageIndex{3.9.5}$

Take the equation

$$\vec{x}' = \left[ \begin{array}{cc} \frac{1}{t} & -1\\ 1 & \frac{1}{t} \end{array} \right] \vec{x}+ \left[ \begin{array}{c} t^2 \\ -t \end{array} \right].$$

1. Check that $$\vec{x}_c = c_1\left[ \begin{array}{c} t \sin t\\ -t \cos t \end{array} \right] + c_2\left[ \begin{array}{c} t \cos t\\ t \sin t \end{array} \right]$$ is the complementary solution.
2. Use variation of parameters to find a particular solution.

Exercise $\PageIndex{3.9.6}$

Find a particular solution to $x' = 5x +4y+t,\: y'=x+8y-t$,

1. using integrating factor method,
2. using eigenvector decomposition,
3. using undetermined coefficients.

Answer

The general solution is (particular solutions should agree with one of these): $x(t)=C_{1}e^{9t}+4C_{2}e^{4t}-\frac{t}{3}-\frac{5}{54}$, $y(t)=C_{1}e^{9t}-C_{2}e^{4t}+\frac{t}{6}+\frac{7}{216}$

Exercise $\PageIndex{3.9.7}$

Find a particular solution to $x'=y+e^t,\: y'=x+e^t$,

1. using integrating factor method,
2. using eigenvector decomposition,
3. using undetermined coefficients.

Answer

The general solution is (particular solutions should agree with one of these): $x(t)=C_{1}e^{t}+C_{2}e^{-t}+te^{t}$, $y(t)=C_{1}e^{t}-C_{2}e^{-t}+te^{t}$

Exercise $\PageIndex{3.9.8}$

Solve $x'_1=x_2+t, x'_2=x_1+t$ with initial conditions $x_1(0)=1, x_2(0)=2$, using eigenvector decomposition.

Answer

$\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right]\left(\frac{5}{2}e^{t}-t-1\right)+\left[\begin{array}{c}{1}\\{-1}\end{array}\right]\frac{-1}{2}e^{-t}$

Exercise $\PageIndex{3.9.9}$

Solve $x''_1=-3x_1+x_2+t, x''_2=9x_1+5x_2 +\cos(t)$ with initial conditions $x_1(0)=0, x_2(0)=0, x'_1(0)=0, x'_2(0)=0$, using eigenvector decomposition.

Answer

$\vec{x}=\left[\begin{array}{c}{1}\\{9}\end{array}\right]\left(\left(\frac{1}{140}+\frac{1}{120\sqrt{6}}\right)e^{\sqrt{6}t}+\left(\frac{1}{140}+\frac{1}{120\sqrt{6}}\right)e^{-\sqrt{6}t}-\frac{t}{60}-\frac{\cos (t)}{70}\right) +\left[\begin{array}{c}{1}\\{-1}\end{array}\right]\left(\frac{-9}{80}\sin (2t)+\frac{1}{30}\cos (2t)+\frac{9t}{40}-\frac{\cos (t)}{30}\right)$