4.7E: Exercises for Section 4.6
- Last updated
- Aug 18, 2022
- Save as PDF
- Page ID
- 111017
( \newcommand{\kernel}{\mathrm{null}\,}\)
For exercises 1 - 5, examine the graphs. Identify where the vertical asymptotes are located.
1)
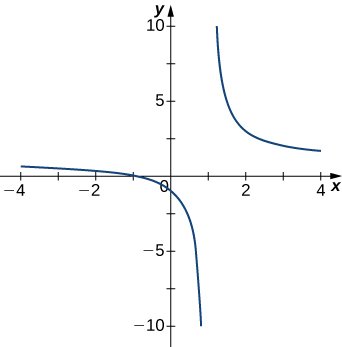
- Answer
- x=1
2)
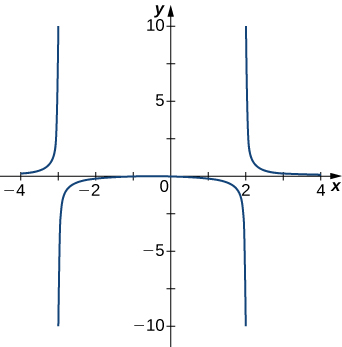
3)
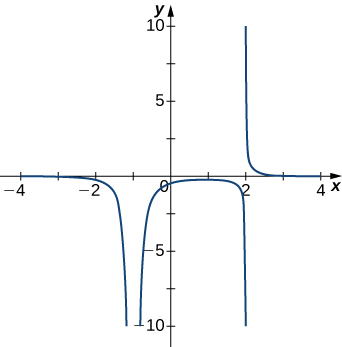
- Answer
- x=−1,x=2
4)
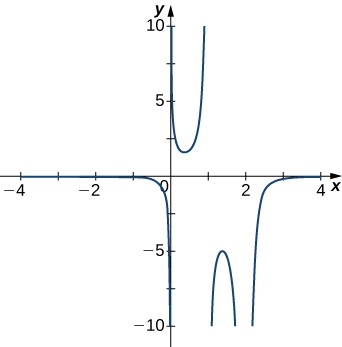
5)
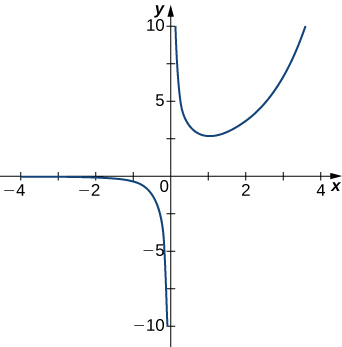
- Answer
- x=0
For the functions f(x) in exercises 6 - 10, determine whether there is an asymptote at x=a. Justify your answer without graphing on a calculator.
6) f(x)=x+1x2+5x+4,a=−1
7) f(x)=xx−2,a=2
- Answer
- Yes, there is a vertical asymptote at x=2.
8) f(x)=(x+2)3/2,a=−2
9) f(x)=(x−1)−1/3,a=1
- Answer
- Yes, there is vertical asymptote at x=1.
10) f(x)=1+x−2/5,a=1
In exercises 11 - 20, evaluate the limit.
11) limx→∞13x+6
- Answer
- limx→∞13x+6=0
12) limx→∞2x−54x
13) limx→∞x2−2x+5x+2
- Answer
- limx→∞x2−2x+5x+2=∞
14) limx→−∞3x3−2xx2+2x+8
15) limx→−∞x4−4x3+12−2x2−7x4
- Answer
- limx→−∞x4−4x3+12−2x2−7x4=−17
16) limx→∞3x√x2+1
17) limx→−∞√4x2−1x+2
- Answer
- limx→−∞√4x2−1x+2=−2
18) limx→∞4x√x2−1
19) limx→−∞4x√x2−1
- Answer
- limx→−∞4x√x2−1=−4
20) limx→∞2√xx−√x+1
For exercises 21 - 25, find the horizontal and vertical asymptotes.
21) f(x)=x−9x
- Answer
- Horizontal: none,
Vertical: x=0
22) f(x)=11−x2
23) f(x)=x34−x2
- Answer
- Horizontal: none,
Vertical: x=±2
24) f(x)=x2+3x2+1
25) f(x)=sin(x)sin(2x)
- Answer
- Horizontal: none,
Vertical: none
26) f(x)=cosx+cos(3x)+cos(5x)
27) f(x)=xsin(x)x2−1
- Answer
- Horizontal: y=0,
Vertical: x=±1
28) f(x)=xsin(x)
29) f(x)=1x3+x2
- Answer
- Horizontal: y=0,
Vertical: x=0 and x=−1
30) f(x)=1x−1−2x
31) f(x)=x3+1x3−1
- Answer
- Horizontal: y=1,
Vertical: x=1
32) f(x)=sinx+cosxsinx−cosx
33) f(x)=x−sinx
- Answer
- Horizontal: none,
Vertical: none
34) f(x)=1x−√x
For exercises 35 - 38, construct a function f(x) that has the given asymptotes.
35) x=1 and y=2
- Answer
- Answers will vary, for example: y=2xx−1
36) x=1 and y=0
37) y=4,x=−1
- Answer
- Answers will vary, for example: y=4xx+1
38) x=0
In exercises 39 - 43, graph the function on a graphing calculator on the window x=[−5,5] and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.
39) [T] f(x)=1x+10
- Answer
- limx→∞1x+10=0 so f has a horizontal asymptote of y=0.
40) [T] f(x)=x+1x2+7x+6
41) [T] limx→−∞x2+10x+25
- Answer
- limx→−∞x2+10x+25=∞
42) [T] limx→−∞x+2x2+7x+6
43) [T] limx→∞3x+2x+5
- Answer
- limx→∞3x+2x+5=3 so this function has a horizontal asymptote of y=3.
In exercises 44 - 55, draw a graph of the functions without using a calculator. Be sure to notice all important features of the graph: local maxima and minima, inflection points, and asymptotic behavior.
44) y=3x2+2x+4
45) y=x3−3x2+4
- Answer
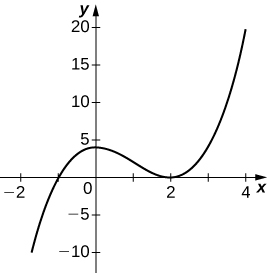
46) y=2x+1x2+6x+5
47) y=x3+4x2+3x3x+9
- Answer
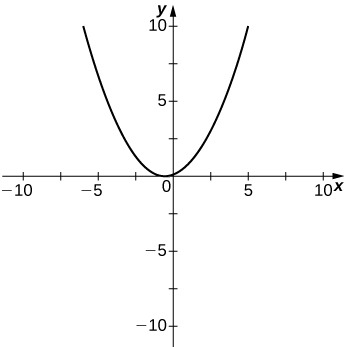
48) y=x2+x−2x2−3x−4
49) y=√x2−5x+4
- Answer
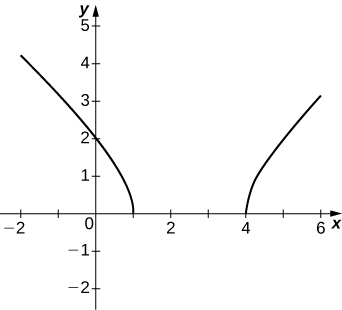
50) y=2x√16−x2
51) y=cosxx, on x=[−2π,2π]
- Answer
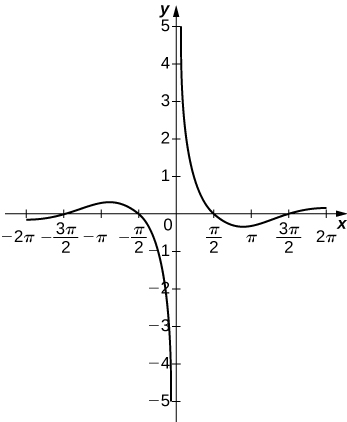
52) y=e^x−x^3
53) y=x\tan x, \quad x=[−π,π]
- Answer
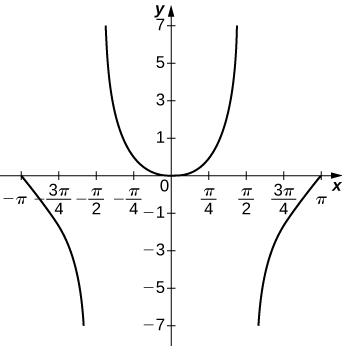
54) y=x\ln(x), \quad x>0
55) y=x^2\sin(x),\quad x=[−2π,2π]
- Answer
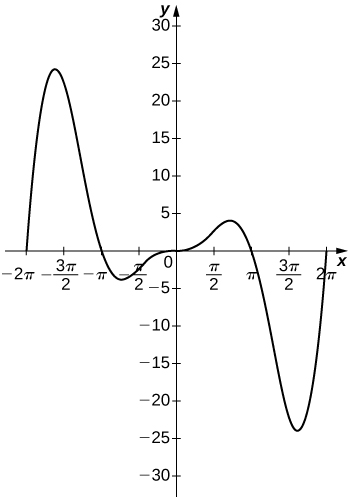
56) For f(x)=\dfrac{P(x)}{Q(x)} to have an asymptote at y=2 then the polynomials P(x) and Q(x) must have what relation?
57) For f(x)=\dfrac{P(x)}{Q(x)} to have an asymptote at x=0, then the polynomials P(x) and Q(x). must have what relation?
- Answer
- Q(x). must have have x^{k+1} as a factor, where P(x) has x^k as a factor.
58) If f′(x) has asymptotes at y=3 and x=1, then f(x) has what asymptotes?
59) Both f(x)=\dfrac{1}{x−1} and g(x)=\dfrac{1}{(x−1)^2} have asymptotes at x=1 and y=0. What is the most obvious difference between these two functions?
- Answer
- \displaystyle \lim_{x→1^−}f(x)=-\infty \text{ and } \lim_{x→1^−}g(x)=\infty
60) True or false: Every ratio of polynomials has vertical asymptotes.

