17.6E: Exercises

Last updated

Aug 13, 2020
Save as PDF
- 17.6: Divide Radical Expressions
- 17.7: Solve Radical Equations

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Exercise SET A: divide square roots

In the following exercises, simplify.

1. a. $\dfrac{\sqrt{128}}{\sqrt{72}}\quad$ b. $\dfrac{\sqrt[3]{128}}{\sqrt[3]{54}}$

2. a. $\dfrac{\sqrt{48}}{\sqrt{75}}\quad$ b. $\dfrac{\sqrt[3]{81}}{\sqrt[3]{24}}$

3. a. $\dfrac{\sqrt{200 m^{5}}}{\sqrt{98 m}}\quad$ b. $\dfrac{\sqrt[3]{54 y^{2}}}{\sqrt[3]{2 y^{5}}}$

4. a. $\dfrac{\sqrt{108 n^{7}}}{\sqrt{243 n^{3}}}\quad$ b. $\dfrac{\sqrt[3]{54 y}}{\sqrt[3]{16 y^{4}}}$

5. a. $\dfrac{\sqrt{75 r^{3}}}{\sqrt{108 r^{7}}}\quad$ b. $\dfrac{\sqrt[3]{24 x^{7}}}{\sqrt[3]{81 x^{4}}}$

6. a. $\dfrac{\sqrt{196 q}}{\sqrt{484 q^{5}}}\quad$ b. $\dfrac{\sqrt[3]{16 m^{4}}}{\sqrt[3]{54 m}}$

7. a. $\dfrac{\sqrt{108 p^{5} q^{2}}}{\sqrt{3 p^{3} q^{6}}}\quad$ b. $\dfrac{\sqrt[3]{-16 a^{4} b^{-2}}}{\sqrt[3]{2 a^{-2} b}}$

8. a. $\dfrac{\sqrt{98 r s^{10}}}{\sqrt{2 r^{3} s^{4}}}\quad$ b. $\dfrac{\sqrt[3]{-375 y^{4} z^{2}}}{\sqrt[3]{3 y^{-2} z^{4}}}$

9. a. $\dfrac{\sqrt{320 m n^{-5}}}{\sqrt{45 m^{-7} n^{3}}}\quad$ b. $\dfrac{\sqrt[3]{16 x^{4} y^{-2}}}{\sqrt[3]{-54 x^{-2} y^{4}}}$

10. a. $\dfrac{\sqrt{810 c^{-3} d^{7}}}{\sqrt{1000 c d}}\quad$ b. $\dfrac{\sqrt[3]{24 a^{7} b^{-1}}}{\sqrt[3]{-81 a^{-2} b^{2}}}$

11. $\dfrac{\sqrt{56 x^{5} y^{4}}}{\sqrt{2 x y^{3}}}$

12. $\dfrac{\sqrt{72 a^{3} b^{6}}}{\sqrt{3 a b^{3}}}$

13. $\dfrac{\sqrt[3]{48 a^{3} b^{6}}}{\sqrt[3]{3 a^{-1} b^{3}}}$

14. $\dfrac{\sqrt[3]{162 x^{-3} y^{6}}}{\sqrt[3]{2 x^{3} y^{-2}}}$

Answer

1. a. $\dfrac{4}{3}$ b. $\dfrac{4}{3}$

3. a. $\dfrac{10 m^{2}}{7}$ b. $\dfrac{3}{y}$

5. a. $\dfrac{5}{6 r^{2}}$ b. $\dfrac{2x}{3}$

7. a. $\dfrac{6 p}{q^{2}}$ b. $-\dfrac{2 a^{2}}{b}$

9. a. $\dfrac{8 m^{4}}{3 n^{4}}$ b. $-\dfrac{2 x^{2}}{3 y^{2}}$

11. $4 x^{4} \sqrt{7 y}$

13. $2 a b \sqrt[3]{2 a}$

Exercise SET B: Rationalize a One Term Denominator

In the following exercises, rationalize the denominator.

15. a. $\dfrac{10}{\sqrt{6}}\quad$ b. $\sqrt{\dfrac{4}{27}}\quad$ c. $\dfrac{10}{\sqrt{5 x}}$

16. a. $\dfrac{8}{\sqrt{3}}\quad$ b. $\sqrt{\dfrac{7}{40}}\quad$ c. $\dfrac{8}{\sqrt{2 y}}$

17. a. $\dfrac{6}{\sqrt{7}}\quad$ b. $\sqrt{\dfrac{8}{45}}\quad$ c. $\dfrac{12}{\sqrt{3 p}}$

18. a. $\dfrac{4}{\sqrt{5}}\quad$ b. $\sqrt{\dfrac{27}{80}}\quad$ c. $\dfrac{18}{\sqrt{6 q}}$

19. a. $\dfrac{1}{\sqrt[3]{5}}\quad$ b. $\sqrt[3]{\dfrac{5}{24}}\quad$ c. $\dfrac{4}{\sqrt[3]{36 a}}$

20. a. $\dfrac{1}{\sqrt[3]{3}}\quad$ b. $\sqrt[3]{\dfrac{5}{32}}\quad$ c. $\dfrac{7}{\sqrt[3]{49 b}}$

21. a. $\dfrac{1}{\sqrt[3]{11}}\quad$ b. $\sqrt[3]{\dfrac{7}{54}}\quad$ c. $\dfrac{3}{\sqrt[3]{3 x^{2}}}$

22. a. $\dfrac{1}{\sqrt[3]{13}}\quad$ b. $\sqrt[3]{\dfrac{3}{128}}\quad$ c. $\dfrac{3}{\sqrt[3]{6 y^{2}}}$

23. a. $\dfrac{1}{\sqrt[4]{7}}\quad$ b. $\sqrt[4]{\dfrac{5}{32}}\quad$ c. $\dfrac{4}{\sqrt[4]{4 x^{2}}}$

24. a. $\dfrac{1}{\sqrt[4]{4}}\quad$ b. $\sqrt[4]{\dfrac{9}{32}}\quad$ c. $\dfrac{6}{\sqrt[4]{9 x^{3}}}$

25. a. $\dfrac{1}{\sqrt[4]{9}}\quad$ b. $\sqrt[4]{\dfrac{25}{128}}\quad$ c. $\dfrac{6}{\sqrt[4]{27 a}}$

26. a. $\dfrac{1}{\sqrt[4]{8}}\quad$ b. $\sqrt[4]{\dfrac{27}{128}}\quad$ c. $\dfrac{16}{\sqrt[4]{64 b^{2}}}$

Answer

15. a. $\dfrac{5 \sqrt{6}}{3}$ b. $\dfrac{2 \sqrt{3}}{9}$ c. $\dfrac{2 \sqrt{5 x}}{x}$

17. a. $\dfrac{6 \sqrt{7}}{7}$ b. $\dfrac{2 \sqrt{10}}{15}$ c. $\dfrac{4 \sqrt{3 p}}{p}$

19. a. $\dfrac{\sqrt[3]{25}}{5}$ b. $\dfrac{\sqrt[3]{45}}{6}$ c. $\dfrac{2 \sqrt[3]{6 a^{2}}}{3 a}$

21. a. $\dfrac{\sqrt[3]{121}}{11}$ b. $\dfrac{\sqrt[3]{28}}{6}$ c. $\dfrac{\sqrt[3]{9 x}}{x}$

23. a. $\dfrac{\sqrt[4]{343}}{7}$ b. $\dfrac{\sqrt[4]{40}}{4}$ c. $\dfrac{2 \sqrt[4]{4 x^{2}}}{x}$

25. a. $\dfrac{\sqrt[4]{9}}{3}$ b. $\dfrac{\sqrt[4]{50}}{4}$ c. $\dfrac{2 \sqrt[4]{3 a^{2}}}{a}$

Exercise SET C: Rationalize a Two Term Denominator

In the following exercises, simplify.

27. $\dfrac{8}{1-\sqrt{5}}$

28. $\dfrac{7}{2-\sqrt{6}}$

29. $\dfrac{6}{3-\sqrt{7}}$

30. $\dfrac{5}{4-\sqrt{11}}$

31. $\dfrac{\sqrt{3}}{\sqrt{m}-\sqrt{5}}$

32. $\dfrac{\sqrt{5}}{\sqrt{n}-\sqrt{7}}$

33. $\dfrac{\sqrt{2}}{\sqrt{x}-\sqrt{6}}$

34. $\dfrac{\sqrt{7}}{\sqrt{y}+\sqrt{3}}$

35. $\dfrac{\sqrt{r}+\sqrt{5}}{\sqrt{r}-\sqrt{5}}$

36. $\dfrac{\sqrt{s}-\sqrt{6}}{\sqrt{s}+\sqrt{6}}$

37. $\dfrac{\sqrt{x}+\sqrt{8}}{\sqrt{x}-\sqrt{8}}$

38. $\dfrac{\sqrt{m}-\sqrt{3}}{\sqrt{m}+\sqrt{3}}$

Answer

27. $-2(1+\sqrt{5})$

29. $3(3+\sqrt{7})$

31. $\dfrac{\sqrt{3}(\sqrt{m}+\sqrt{5})}{m-5}$

33. $\dfrac{\sqrt{2}(\sqrt{x}+\sqrt{6})}{x-6}$

35. $\dfrac{(\sqrt{r}+\sqrt{5})^{2}}{r-5}$

37. $\dfrac{(\sqrt{x}+2 \sqrt{2})^{2}}{x-8}$

Exercise SET D: writing exercises

1. Simplify $\sqrt{\dfrac{27}{3}}$ and explain all your steps.
2. Simplify $\sqrt{\dfrac{27}{5}}$ and explain all your steps.
3. Why are the two methods of simplifying square roots different?
Explain what is meant by the word rationalize in the phrase, "rationalize a denominator."
Explain why multiplying $\sqrt{2x}-3$ by its conjugate results in an epxression with no radicals.
Explain why multiplying $\dfrac{7}{\sqrt[3]{x}}$ by $\dfrac{\sqrt[3]{x}}{\sqrt[3]{x}}$ does not rationalize the denominator.

Answer

1. Answers will vary

3. Answers will vary

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

This table has 4 rows and 4 columns. The first row is a header row and it labels each column. The first column header is â€œI canâ€¦â€, the second is â€œConfidentlyâ€, the third is â€œWith some helpâ€, and the fourth is â€œNo, I donâ€™t get itâ€. Under the first column are the phrases â€œdivide radical expressions.â€, â€œrationalize a one term denominatorâ€, and â€œrationalize a two term denominatorâ€. The other columns are left blank so that the learner may indicate their mastery level for each topic. — Figure 8.5.63

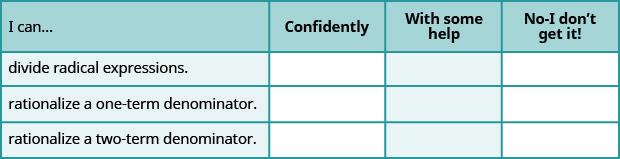
b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

Search

Text Color

Text Size

Margin Size

Font Type

Practice Makes Perfect

Exercise SET A: divide square roots

Exercise SET B: Rationalize a One Term Denominator

Exercise SET C: Rationalize a Two Term Denominator

Exercise SET D: writing exercises

Self Check

Practice Makes Perfect

Exercise SET A: divide square roots

Exercise SET B: Rationalize a One Term Denominator

Exercise SET C: Rationalize a Two Term Denominator

Exercise SET D: writing exercises

Self Check

Support Center

How can we help?