5.2: Place Value Systems
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Positional System
In a place value system, also called a positional system, the placement of the symbols in a numeral determines the value of the symbols.
For example in the numeral 73, the 7 represents seven tens and the 3 represents three ones, or seventy-three. However, if we switched the order to 37, the 3 would represent three tens and the 7 would represent seven ones, or thirty-seven.
The number system we use today is the Hindu-Arabic system which uses a place value system involving powers of ten. (Base 10) This was not the first place value system and civilizations used bases other than 10. As you might imagine, the development of a base system is an important step in making the counting process more efficient. Our own base-ten system probably arose from the fact that we have 10 fingers (including thumbs) on two hands. This is a natural development. However, other civilizations have had a variety of bases other than ten. For example, the Natives of Queensland used a base-two system, counting as follows: “one, two, two and one, two two’s, much.” Some Modern South American Tribes have a base-five system counting in this way: “one, two, three, four, hand, hand and one, hand and two,” and so on. The Babylonians used a base-sixty (sexigesimal) system. We wrap up with a specific example of a civilization that actually used a base system other than 10.
The Mayan Civilization
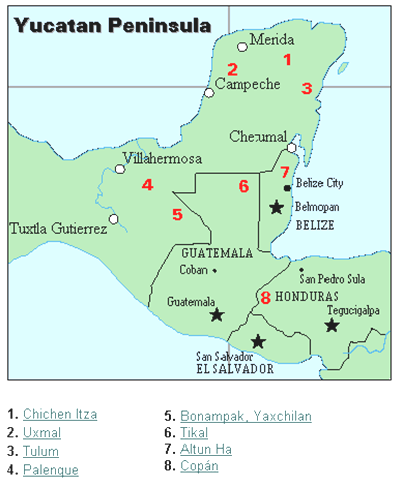 The Mayan civilization is generally dated from 1500 B.C.E to 1700 C.E. The Yucatan Peninsula (see map[i]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[ii] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
The Mayan civilization is generally dated from 1500 B.C.E to 1700 C.E. The Yucatan Peninsula (see map[i]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[ii] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
 There were two numeral systems developed by the Mayans - one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[iii] like the sample to the left[iv] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 18, since 18×20=360.
There were two numeral systems developed by the Mayans - one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[iii] like the sample to the left[iv] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 18, since 18×20=360.
The Mayan Number System
We will focus on the numeration system of the “priestly”. As we stated earlier, the Mayans used a slightly modified base-20 system, called the “vigesimal” system. Like our system, it is positional, meaning that the position of a numeric symbol indicates its place value. In the following table you can see the place value in its vertical format.[v]
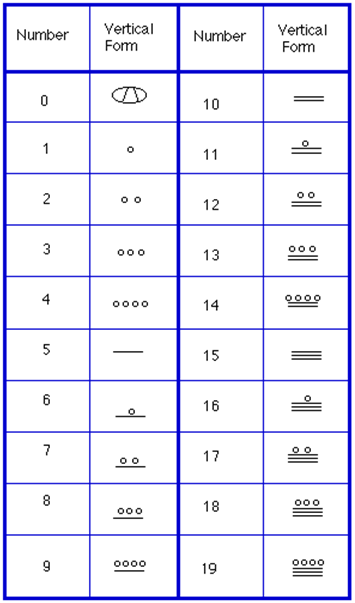 Powers Base-Ten Value 20×18×20720020×18360201202001
Powers Base-Ten Value 20×18×20720020×18360201202001
In order to write numbers down, there were only three symbols needed in this system. A horizontal bar represented the quantity 5, a dot represented the quantity 1, and a special symbol (thought to be a shell) represented zero. The Mayan system may have been the first to make use of zero as a placeholder/number. The first 20 numbers are shown in the table to the right.[vi]
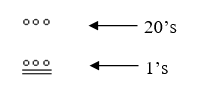
Unlike our system, where the ones place starts on the right and then moves to the left, the Mayan systems places the ones on the bottom of a vertical orientation and moves up as the place value increases.
When numbers are written in vertical form, there should never be more than four dots in a single place. When writing Mayan numbers, every group of five dots becomes one bar. Also, there should never be more than three bars in a single place…four bars would be converted to one dot in the next place up. It’s the same as 10 getting converted to a 1 in the next place up when we carry during addition.
What is the value of this number, which is shown in vertical form?

Solution
Starting from the bottom, we have the ones place. There are two bars and three dots in this place. Since each bar is worth 5, we have 13 ones when we count the three dots in the ones place. Looking to the place value above it (the twenties places), we see there are three dots so we have three twenties.
Hence we can write this number in base-ten as:
(3×201)+(13×200)=(3×20)+(13×1)=60+13=73
What is the value of the following Mayan number?
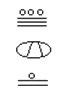
Solution
This number has 11 in the ones place, zero in the 20’s place, and 18 in the 360’s place. Hence, the value of this number in base-ten is:
18×360+0×20+11×1=6491
Convert the base 10 number 375710 to Mayan numerals.
Solution
The highest place value that will divide into 3757 is 360 so we start by dividing that and then proceed from there:
3757÷360=10R157157÷20=7R17
This number indicates that we have 17 in the ones position. That’s three bars and two dots at the bottom of the number. We also have 7 in the 20’s place, so that’s one bar and two dots in the second position. Finally, we have 10 in the 360’s place, so that’s two bars on the top. We get the following

Convert the base 10 number 1055310 to Mayan numerals.
- Answer
-

We have only scratched the surface of the wealth of research and information that exists on the development of numbers and counting throughout human history. What is important to note is that the system that we use every day is a product of thousands of years of progress and development. It represents contributions by many civilizations and cultures. It does not come down to us from the sky, a gift from the gods. It is not the creation of a textbook publisher. It is indeed as human as we are, as is the rest of mathematics. Behind every symbol, formula and rule there is a human face to be found, or at least sought.
The Evolution of the Hindu-Arabic System
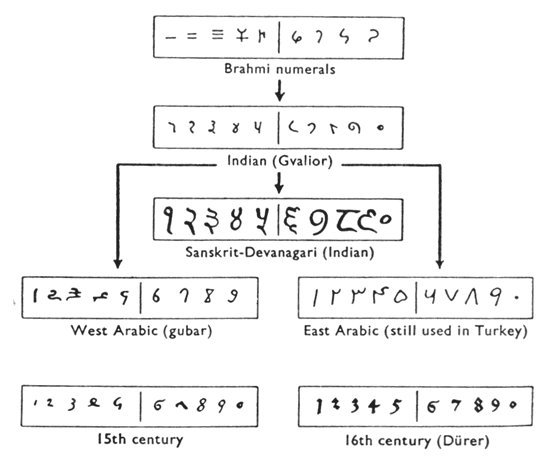
Our own number system, composed of the ten symbols {0,1,2,3,4,5,6,7,8,9} is called the Hindu-Arabic system. This is a base-ten (decimal) system since place values increase by powers of ten. Furthermore, this system is positional, which means that the position of a symbol has bearing on the value of that symbol within the number. For example, the position of the symbol 3 in the number 435,681 gives it a value much greater than the value of the symbol 8 in that same number. We’ll explore base systems more thoroughly later. The development of these ten symbols and their use in a positional system comes to us primarily from India.[viii]
 It was not until the 15th century that the symbols that we are familiar with today first took form in Europe. However, the history of these numbers and their development goes back hundreds of years. One important source of information on this topic is the writer al-Biruni, whose picture is shown here.[ix] Al-Biruni, who was born in modern day Uzbekistan, had visited India on several occasions and made comments on the Indian number system. When we look at the origins of the numbers that al-Biruni encountered, we have to go back to the third century B.C.E. to explore their origins. It is then that the Brahmi numerals were being used.
It was not until the 15th century that the symbols that we are familiar with today first took form in Europe. However, the history of these numbers and their development goes back hundreds of years. One important source of information on this topic is the writer al-Biruni, whose picture is shown here.[ix] Al-Biruni, who was born in modern day Uzbekistan, had visited India on several occasions and made comments on the Indian number system. When we look at the origins of the numbers that al-Biruni encountered, we have to go back to the third century B.C.E. to explore their origins. It is then that the Brahmi numerals were being used.
The Brahmi numerals were more complicated than those used in our own modern system. They had separate symbols for the numbers 1 through 9, as well as distinct symbols for 10, 100, 1000,…, also for 20, 30, 40,…, and others for 200, 300, 400, …, 900. The Brahmi symbols for 1, 2, and 3 are shown below.[x]
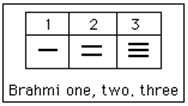
These numerals were used all the way up to the 4th century C.E., with variations through time and geographic location. For example, in the first century C.E., one particular set of Brahmi numerals took on the following form[xi]:

From the 4th century on, you can actually trace several different paths that the Brahmi numerals took to get to different points and incarnations. One of those paths led to our current numeral system, and went through what are called the Gupta numerals. The Gupta numerals were prominent during a time ruled by the Gupta dynasty and were spread throughout that empire as they conquered lands during the 4th through 6th centuries. They have the following form[xii]:

How the numbers got to their Gupta form is open to considerable debate. Many possible hypotheses have been offered, most of which boil down to two basic types[xiii]. The first type of hypothesis states that the numerals came from the initial letters of the names of the numbers. This is not uncommon…the Greek numerals developed in this manner. The second type of hypothesis states that they were derived from some earlier number system. However, there are other hypotheses that are offered, one of which is by the researcher Ifrah. His theory is that there were originally nine numerals, each represented by a corresponding number of vertical lines. One possibility is this:[xiv]

Because these symbols would have taken a lot of time to write, they eventually evolved into cursive symbols that could be written more quickly. If we compare these to the Gupta numerals above, we can try to see how that evolutionary process might have taken place, but our imagination would be just about all we would have to depend upon since we do not know exactly how the process unfolded.
The Gupta numerals eventually evolved into another form of numerals called the Nagari numerals, and these continued to evolve until the 11th century, at which time they looked like this:[xv]

Note that by this time, the symbol for 0 has appeared! The Mayans in the Americas had a symbol for zero long before this, however, as we shall see later in the chapter.
These numerals were adopted by the Arabs, most likely in the eighth century during Islamic incursions into the northern part of India.[xvi] It is believed that the Arabs were instrumental in spreading them to other parts of the world, including Spain (see below).
Other examples of variations up to the eleventh century include:
Devangari, eighth century[xvii]:

West Arab Gobar, tenth century[xviii]:

Finally, one more graphic[xx] shows various forms of these numerals as they developed and eventually converged to the 15th century in Europe.
Galley Multiplication
In the 1500s in England, students were taught to compute multiplication following galley method.
To multiply 43 and 218, for example, draw a 2 × 3 grid of squares. Write the digits of the first number along the right side of the grid and the digits of the second number along the top.
Divide each cell of the grid diagonally and write in the product of the column digit and row digit of that cell, separating the tens from the units across the diagonal of that cell. (If the product is a one digit answer, place a 0 in the tens place.)
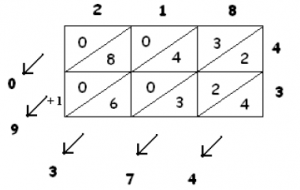
To get the answer, add the entries in each diagonal, carrying tens digits over to the next diagonal if necessary. In our example, we have
218×43=9374.
Lines and Intersections
Here’s an unusual way to perform multiplication. To compute 22 × 13, for example, draw two sets of vertical lines, the left set containing two lines and the right set two lines (for the digits in 22) and two sets of horizontal lines, the upper set containing one line and the lower set three (for the digits in 13).
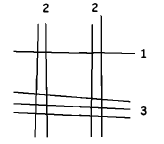
There are four sets of intersection points. Count the number of intersections in each and add the results diagonally as shown:
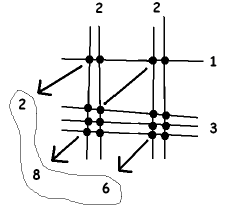
The answer 286 appears!
There is one possible glitch as illustrated by the computation 246 × 32:
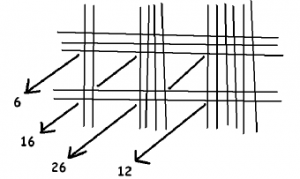
Although the answer 6 thousands, 16 hundreds, 26 tens, and 12 ones is absolutely correct, one needs to carry digits and translate this as 7,872.
[i] www.gorp.com/gorp/location/latamer/map_maya.htm
[ii] Bidwell, James; Mayan Arithmetic in Mathematics Teacher, Issue 74 (Nov., 1967), p. 762-68.
[iii] www.ukans.edu/~lctls/Mayan/numbers.html
[iv] www.ukans.edu/~lctls/Mayan/numbers.html
[v] Bidwell
[vi] www.vpds.wsu.edu/fair_95/gym/UM001.html
[vii] forum.swarthmore.edu/k12/mayan.math/mayan2.html
[viii] www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html
[ix] www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Al-Biruni.html
[x] www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html
[xi] www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html
[xii] Ibid
[xiii] Ibid
[xiv] Ibid
[xv] Ibid
[xvi] Katz, page 230
[xvii] Burton, David M., History of Mathematics, An Introduction, p. 254-255
[xviii] Ibid
[xix] Ibid
[xx] Katz, page 231.



