Skip to main content
Mathematics LibreTexts

9.4: Geometric Symmetry and Tessellations

  1. Last updated
  2. Save as PDF
  • Page ID
    99772

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Rigid Motion

    A rigid motion is the action of taking a geometric object in the plane and moving it is some fashion to another position in the plane without changing its shape or size. This is also called a transformation.

    Translation

    A translation is a transformation that moves a figure (without altering dimensions) to a new position along a line segment.

    Example 1

    alt

    Reflection

    A reflection is a transformation that moves an object so that the ending position is a mirror image of the object in its starting position.

    Example 2

    alt

    Rotation

    A rotation is a transformation where a figure is rotated about its center by a specified amount (given usually in degrees).

    Example 3

    alt

    Glide Reflection

    A glide reflection is a transformation formed by performing a translation followed by a reflection.

    Example 4

    alt

    Example 5

    Consider the equilateral triangle below. What rigid motions can we do to it that will result in the triangle occupying the same space? What happens if we combine rigid motions?

    alt

    Try it Now 1

    Consider a square. What rigid motions can we do to it that will result in the square occupying the same space? What happens if we combine rigid motions? Keep in mind that "doing nothing" is also a rigid motion.

    Answer

    Square.png

    In 2D geometry, a figure is symmetrical if an operation can be done to it that leaves the figure occupying an identical physical space. This can be accomplished in two ways.

    Line symmetry

    Line symmetry occurs when a line may be passed through an object such that both halves of the object perfectly mirror each other.

    Example 6

    Consider the triangle below. An equilateral triangle has three instances of line symmetry: one from each vertex to the midpoint of the opposite side.

    alt

    Rotational Symmetry

    Rotational symmetry occurs when a shape may be rotated to occupy the same space as the original.

    Example 7

    Let's take the same triangle again. An equilateral triangle has three degrees of rotational symmetry: at 120, 240, and 360 degrees. Once we have determined rotational symmetry to 360 degrees, we can stop, as the pattern will repeat itself after that.

    alt

    Symmetry in Art

    Symmetry in art is used as a way to emphasize beauty and order. The human brain finds symmetry to be attractive and beautiful. For this reason, artists attempt to emphasize (at certain times and using certain methods) the symmetry of their subject or surroundings.

    Triskelions - an example of rotational symmetry.

    965px-Triple-Spiral-Symbol.svg.png

    Tessellations

    Tessellation

    A tessellation is a design using one ore more geometric shapes with no overlaps and no gaps. The idea is that the design could be continued infinitely far to cover the whole plane (though of course we can only draw a small portion of it).

    See the photos below [1] for examples.

    tritesselate-225x244.png 512px-Uniform_tiling_333-t012.png 512px-Snub_square_rhombic_tiling_2.png

    Many tessellations have translational symmetry, but it’s not strictly necessary. The Penrose tiling shown below [2] does not have any translational symmetry.

    256px-Penrose_Tiling_Rhombi.svg_.png

    It’s actually much harder to come up with these “aperiodic” tessellations than to come up with ones that have translational symmetry. So we’ll focus on how to make symmetric tessellations.

    The first two tessellations above were made with a single geometric shape (called a tile) designed so that they can fit together without gaps or overlaps. The third design uses two basic tiles. Tessellations are often called tilings, and that’s what you should think about: If I had tiles made in this shape, could I use them to tile my kitchen floor? Or would it be impossible?

    Try it Now 2

    Work on these exercises on your own. You will need lots of copies (maybe 10–15 each) of each shape below. Focus on just a single tile for making your tessellation.

    1. Start with the square tile. Can you fit the squares together in a pattern that could be continued forever, with no gaps and no overlaps? Can you do it in more than one way?
    2. Now try one of the triangular tiles. Can you use many copies of a single triangle to tessellate the plane?
    3. Repeat this process with each of the other tiles. Keep track of your findings.

    square2-300x297-1.png

    tessrect-300x114.png

    tessquad3-300x120.png

    tessquad2-300x212.png

    tessquad1-300x270.png

    eqtri.png

    tesstria-300x140.png

    tesstrib-300x114.png

    pentagon-300x277.png

    pent1-225x300.png

    hexagon-300x255.png

    heptagon-300x287.png

    octagon-300x293.png

    Answer

    Answers may vary

    Which of the tiles given above tessellate, and which do not?

    Do you have any conjectures based on this experience, about which shapes will tessellate and which will not?

    Theorem: Tessellations

    Any triangle will tessellate. So will any quadrilateral.

    The explanation for this comes down to what you know about the sums of angles. The sum of the angles in a triangle is 180°.

    tesstri1-300x99.png

    So if you make six copies of a single triangle and put them together at a point so that each angle appears twice, there will be a total of 360° around the point, meaning the triangles fit together perfectly with no gaps and no overlaps.

    tesstri2-300x102.png

    You can then repeat this at every vertex, using more and more copies of the same triangles.

    tesstri3-300x92.png

    Escher Drawings

    The artist M.C. Escher created many works of art inspired by mathematics, including some very beautiful tessellations. Below you will see some images [3] inspired by his work. You can view the real thing at http://www.mcescher.com/ in the “Symmetry” gallery.

    birds-300x200.jpg lizards-300x214.jpg

    You can make your own Escher-like drawings using some facts that you learned while studying tessellations.

    Try it Now 3

    Here’s how you can create your own Escher-like drawings.

    1. Select your basic tile. The first time you do this, it’s easiest to start with a simple shape that you know will tessellate, like an equilateral triangle, a square, or a regular hexagon.
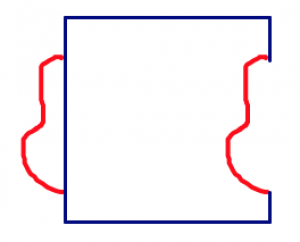
    2. Draw a “squiggle” on one side of your basic tile.

    eschdirect1-225x219.png

    1. Cut out the squiggle, and move it to another side of your shape. You can either translate it straight across or rotate it.
    eschdirect2-300x242.png

    or

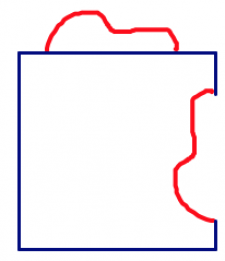    		 eschdirect3-225x261.png
    1. It’s important that the cut-out lines up along the new edge in the same place that it appeared on its original edge.
    2. Tape the squiggle into its new location. This is your basic tile. On a large piece of paper, trace around your tile. Then move it the same way you moved the squiggle (translate or rotate) so that the squiggle fits in exactly where you cut it out.

    eschdirect4-768x739.png

    1. The shape will still tessellate, so go ahead and fill up your paper.
    2. Now get creative. Color in your basic shape to look like something — an animal? a flower? a colorful blob? Add color and design throughout the tessellation to transform it into your own Escher-like drawing.
    3. If you want to try a more complicated version, cut two different squiggles out of two different sides, and move them both.
    Answer

    Answers will vary

    1. Triangular tessellation from pixababy [CC0]. Hexagonal and rhombic tessellations from Wikimedia Commons [Public domain]. ↵
    2. Image via Wikimedia Commons [Public donmain]. ↵
    3. Images from flickr [CC BY-NC-SA 2.0]. Birds by Sharon Drummond. Lizard tiles by Ben Lawson. ↵

    This page titled 9.4: Geometric Symmetry and Tessellations is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by Pamini Thangarajah.